Resolução Comentada – Dinâmica Impulsiva

Resolução Comentada

Dinâmica Impulsiva

 

 

01- Teorema do Impulso  —   “ O impulso da força resultante de um sistema de forças que age sobre um corpo é igual à variação da quantidade de movimento do corpo”

 F. ∆t=m. ∆V  —  F. ∆t=m.V/2  —  F=mV/2∆t  —  R- D

02- Dados  —   m = 0,8 kg  — v_o = 93,6 km/h = 26 m/s  —   v = 280,8 km/h = 78 m/s  —  o enunciado afirma que antes da colisão a velocidade relativa entre a mola e o capacete é V_R=78 – 26=52m/s, e no instante após a colisão a velocidade relativa é nula  —  assim, a quantidade de movimento da mola após a colisão em relação ao capacete é nula  —  I=ΔQ  —  F.Δt=mΔV  —  F.Δt=m.(V – V_o)  —  F.0,026=0,8.(52 – 0)  —  F=1.600N   —  R- B

03- Em todo gráfico F x t, o impulso é numericamente igual a área compreendida entre a reta

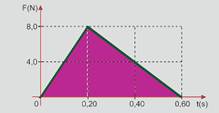
representativa e o eixo t, no caso a área do triângulo  —  I=b.h/2=0,6.8,0/2  —  I=2,4N.s.

Pelo Teorema do Impulso  —   o impulso da força resultante é igual à variação da quantidade de movimento (ΔQ)  —  I = ΔQ = m Δv  —  2,4 = 0,1 (v – 0)  —   v = 24 m/s  —  R- C

04- Quantidade de movimento antes da explosão  —  Q_a=0  —  quantidade de movimento do sistema depois da explosão  — Qd=M₁.₁ + M₂.V₂=234.10^-3.1,0.10² + 4.10^-3.V₂  —  Q_d=234.10^-1 – 4.10^-3.V₂  —  Q_a=Q_d  —  0=234.10^-1 – 4.10^-3.V₂  —  V₂=5,85.10³m/s.

A variação da energia cinética da partícula fornece o trabalho (W) necessário para pará-la  —  E_ca=0  —  E_cd=mV_d²/2=234.10^-3(1,0.10²)²/2 +4.10^-3.(5,85.10³)²/2  — W=E_cd – E_ca= – 6,8.10⁴J  —  mas, o trabalho também é fornecido por  — W=F.d.cos180^o  —   – 6,8.10⁴=F.10.(-1)  —  F=6,8.10³N  —  R- D

05-  Observe na figura abaixo o esquema do enunciado do exercício antes e depois do fenômeno (escorregamento da ave)  —

Quantidade de movimento do sistema (ave + tronco) antes  —  Q_sa=50.(+2) + 10.(-2)=80kg.m/s  —  quantidade de movimento do sistema (ave + tronco) depois  —  Q_sd=50.(V) + 10.(-0,5)=50V – 5  —  Q_sa=Q_sd  —  80=50V – 5  —  V=1,7m/s  —   R- D

06- Observe a figura fornecida  —  orientando a trajetória como positiva no sentido do movimento da sonda (positivo para a esquerda).

Antes – bola chegando à sonda  com velocidade de 2.000m/s e a sonda inicialmente parada  —  Q_a=m_b.V_b + m_s.V_s=10 x 2.000 + 1.000 x 0  —  Q_a=20.000kg.m/s.

Depois – bola saindo com velocidade Vb=-2000/5=- 400m/s e a sonda se movendo para a esquerda com velocidade +V  —  Q_d=m_b.V_b + m_s.(+V)=10.( – 400) + 1.000V  —  Q_d= – 4.000 + 1.000V  —  Q_a=Q_d  —  20.000= – 4.000 + 1.000V  —  V=24m/s  —  R- E

07- Como a direção e o sentido da velocidade coincidem com a direção e sentido da quantidade de movimento, e como a quantidade de movimento do sistema antes da explosão é nula, depois da explosão também deverá ser nula. Assim, a única alternativa em que todos os vetores se anulam é a D  —  R- D

08- Como os caixotes tem a mesma massa, e os choques são perfeitamente elásticos, em todos os choques eles trocam ou conservam suas velocidades conforme você pode observar nos esquemas abaixo: 

Observe que após o 3^o choque, V_A=0 e V_B=V_o  —  R- E

09- Trata-se de uma colisão perfeitamente elástica com esferas de mesma massa onde elas trocam suas velocidades  —  o coeficiente de restituição vale e=1  —  a energia cinética se conserva (as velocidades são iguais antes e depois da colisão)  —  em qualquer tipo de colisão a quantidade de movimento sempre se conserva  —  R- D

10- Dados  —  m₁ = 800 kg  —   v₁ = 90 km/h = 25 m/s  —   m₂ = 450 kg e v₂= 120 km/h =120/3,6=100/3 m/s  —  lembre-se de que você não deve fazer uma divisão que dá dízima no meio da solução de um exercício  —  trabalhe com a fração  —  se na resposta final a dízima persistir, aí sim, você faz as contas e os arredondamentos  — observe que se fosse feita a divisão nessa questão, dividindo 100/3 e obtendo 33,3 m/s para v₂, você teria muito trabalho e não chegaria à resposta exata.  —  módulo da quantidade de movimento dos dois carros antes da colisão  —  Q₁=m₁.V₁=800.25  — Q₁=20.10³kg.m/s  —  Q₂=m₂.V₂=450.100/3  —  Q₂=15.10³kg.m/s —  quantidade de movimento do

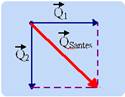
sistema antes da colisão, que são perpendiculares, pois as velocidades também são  —  como quantidade de movimento é uma grandeza vetorial, como mostra o esquema, vem  —     —  aplicando Pitágoras  —   Q_Santes=(20.10²)² + (15.10²)²  —  Q_Santes=25.10³kg.m/s. 

Sendo a colisão inelástica eles se movem juntos após a mesma, na mesma direção e sentido que  com velocidade V e massa total M  —   M=m₁ + m₂  —  M=1.250kg  —  Q_Sdepois=MV  —  Q_Sdepois =1250V  —  como o sistema é isolado a quantidade de movimento antes e depois do choque é a mesma  —  Q_Santes = Q_Sdepois  —  25.10³=1250V  —  V=20m/s  —  R- B

11- Soma vetorial das quantidades de movimento antes dos choques:

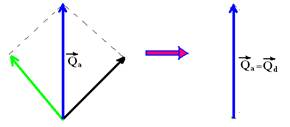
Baseado no Princípio da Conservação da quantidade de Movimento (), dentre todas as alternativas, a única cuja soma vetorial das quantidades de movimento depois do choque também é vertical e para cima é a E  —  R- E

 

Voltar para os exercícios