Aplicações das leis de Newton sem Atrito – Resolução

Resolução Comentada  

Aplicações das leis de Newton sem Atrito

01- As leis de Kepler não justificam a afirmação do astronauta porque elas versam sobre forma da órbita, período da órbita e área varrida na órbita  —  a afirmação explica-se pelo Princípio Fundamental da Dinâmica, pois o que está em questão são a massa e o peso do telescópio  —  como o astronauta e o telescópio estão em órbita, estão sujeitos apenas à força peso, e, consequentemente, à mesma aceleração (centrípeta), que é a da gravidade local, tendo peso

APARENTE nulo  —  F_R=P  —   m a = m g  —  a = g  — a aceleração de queda do telescópio e dos astronautas é a mesma  —  é por esse motivo que os astronautas  flutuam dentro e fora de uma nave e diz-se nesse caso que os corpos estão em estado de imponderabilidade  —  R- D

Observação  —  considerando R = 6.400 km o raio da Terra, à altura h = 540 km, o raio da órbita do telescópio é r = R + h = 6.400 + 540 = 6.940 km  —  de acordo com a lei de Newton da gravitação, a intensidade do campo gravitacional num ponto da órbita é   —  g = g_o.(R/r)², sendo g_o= 10 m/s² (aceleração da gravidade na superfície da Terra)  —  g=10.(6.400/6.940)²  —  g=8,5m/s²  —  ou seja, o peso REAL do telescópio na órbita não é pequeno, é 85% do seu peso na superfície terrestre. 

02- Peso de cada objeto  —  P=m.g  —  P=0,050.10  —  P=0,5N  —  n=peso total (que o fio suporta sem se romper)/peso de cada objeto=5,80/05  —  n=11,6  —  n=12 objetos  —  o fio se rompe entre o suporte e o primeiro objeto, onde a força de tração é maior  —  R- E

03- Observe na figura abaixo que a força  aplicada pelo comerciante sobre o prato foi decomposta em duas parcelas  e . 

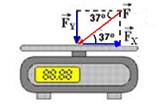
A parcela  horizontal e para a direita não influi na indicação da balança  —   a força adicional aplicada é a parcela vertical  de intensidade  —  sen37^o=F_Y/F  —  0,6=FY/5  —  F_Y=3N  —  assim, uma massa de 1,5kg que pesa P=mg  —P=1,5.10=15N, passará a pesar 18N e terá massa de m=18/10=1,8kg  —  R- D

04- Como despreza-se os atritos, sobre ele não surgem forças horizontais, apenas as verticais que são o peso e a força de contato entre ele e a superfície horizontal  —  essas forças tem sentidos contrários com a parte esquerda do brinquedo descendo e a direita

 Subindo  —  R- D

05- Calculo do peso de uma formiga  —  massa de uma formiga  —  m=20.10^-3g=2.10^-5kg  —  P=mg=2.10^-5.10  —  P=2.10^-4N (peso de uma formiga)  —  a intensidade da força de compressão entre o suporte B e o apoio (N=40.10^-3=4.10^-2N) equivale a duas vezes o peso total (P_f) das formigas, pois, ao mesmo tempo que A ficou P_f mais leve, B ficou P­_f mais pesado  —  P_f=peso total das

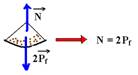
formigas = (número de formigas).(peso de uma formiga)  —  P_f = n.2.10^-4  —  4.10^-2 = 2.(n.2.10^-4)  —  n = 4.10^-2/4.10^-4  —  n = 100 formigas  —  R- B

06- Calculando a massa de um corpo que pesa P=1.000N  —   P=m.g  —  1.000=m.10  —  m=100kg=10²kg  —  R- A

07-

O procedimento I é correto, pois a massa de um corpo é uma grandeza fundamental e que pode ser medida por comparação com massa padrão utilizando uma balança de pratos, onde colocamos

num dos pratos a massa que queremos medir, e no outro,  massas padrão, até que equilibrem a balança. Observe que esse processo independe da intensidade do campo gravitacional (é válido para qualquer planeta), pois sempre será o mesmo para os dois objetos.

  o procedimento II é correto, pois um dinamômetro mede a força de reação ao peso do corpo, que nas condições indicadas é igual ao peso do corpo 

 o procedimento III não é correto, pois corpos de massa diferentes possuem o mesmo tempo de queda

 o procedimento IV é equivalente ao procedimento I e desta forma medirá a massa do corpo e não seu peso.

R- A 

08- Peso do carro  —  P_c=m.g  —  P_c=700.10  —  P_c=7000N  —  chamando de P o peso do

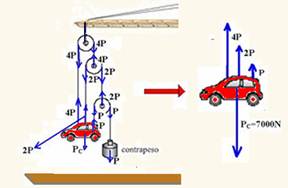
contrapeso, de m sua massa, e colocando todas as forças  —  observe que sobre o carro agem as forças 7P (para cima) o peso do carro P_c=7000N (para baixo)  —  como ele está em equilíbrio  —  7P=P_c  —  7P=7000  —  P=1000N  —   m=100kg (massa mínima do contrapeso)  —   o cabo central exerce uma força de 2P (veja figura)  —  F=2.1000  —  F=2000N  —  R- A

09- Os órgãos internos só se movem ou tendem a se mover, por inércia, quando houver variação de velocidade, ou seja, surgir aceleração, o que só ocorre na alternativa D  —   R- D

10- Colocando as forças que agem sobre o bloco 1 que são  —  seu peso – P₁=mg  —  força com que o bloco 2 age sobre o bloco 1 – N₂₁=N  —  como o bloco 1 sobe com movimento uniformemente

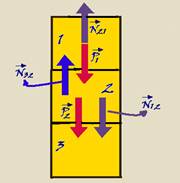
retardado, a resultante das forças sobre ele é para baixo  —F_R=m.a  — mg – N = ma (I).

Forças que agem sobre o bloco 2  —  seu peso – P₂=mg  —  força com que o bloco 1 age sobre o bloco 2 – N₁₂=N  —  força com que o bloco 3 age sobre o bloco 2 – N₃₂  —  como o bloco 2 sobe com movimento uniformemente retardado, a resultante das forças sobre ele é para baixo  —  F_R=ma  —  mg + N – N₃₂ = ma (II)  —  somando as equações (I) com (II)  —  2mg – N₃₂ = 2ma  —  N₃₂ = 2mg – 2ma  —  força que 3 exerce sobre 2  —  N₃₂=2m(g – a)  —  R- D

11- Como o sistema (barco + pessoa + pacote) se movem juntos, eles possuem a mesma aceleração que é fornecida pela segunda lei de Newton  — F_R = m.a  —   240 = (100 + 58 + 2).a  —  240 = 160.a ==> a = 240/160 = 1,5 m/s²  —  apenas sobre o pacote de

2 kg  F = m.a = 2.1,5 = 3,0 N  —  R- C

12- Colocando as forças sobre cada bloco:

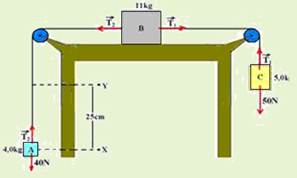
bloco A – sobe  —  F_R=ma  —  T₂  – 40= 4.a (I) 

bloco B – direita  —  F_R=ma  — T₁ – T₂=11.a (II)  

bloco C – desce  —F_R=ma  —  50 – T₁=ma  —  50 – T­₁=5.a (III)

somando (I), (II) e (III)   —  10=20.a   —  a=0,5m/s²  —  o bloco A sobe com aceleração de 0,5m/s², percorrendo ∆S=25cm=0,25m e tendo V_o=0 em X e V em Y  —  aplicando a equação de Torricelli  —V² = Vo_o² + 2.a.∆S  —  V² = 0² + 2.0,5.0,25  —  V=√(0,25)  —  V=0,5m/s  —  R – A

13- Decompondo, na figura I a força de tração T₁  em suas componentes vertical e horizontal, e colocando todas as forças que agem sobre a tora nas duas figuras, você observa que:

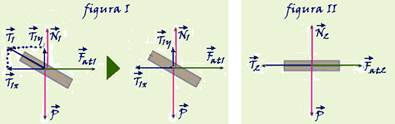
figura I  —  T_1x + N₁=P  —  N₁=P – T_1x              figura II  —  N₂=P  —  portanto N₂>N₁  —  R- B 

Observ. – A intensidade da força de atrito entre a tora e o solo não depende da área de contato entre os mesmos e, assim, F_at1=F_at2 e T_1x=T₂

14-  Como o andaime se encontra parado (equilíbrio estático) a resultante das forças que agem sobre ele ê nula  —   observe que os pesos sobre o andaime encontram-se no meio (peso de um operário + peso do andaime, supondo-o homogêneo) e na extremidade esquerda (peso do outro operário)  —  assim, a tensão na corda X é maior que a na corda Y  —  R- D

15- Forças que agem sobre o balcão na direção do movimento  —  P_P  —  parcela do peso que tenta fazer o bloco descer o plano inclinado  —  P_P=m.g.sen30^o  —  P_P=200.10.0,5  —  P_P=1.000N  —  F  — intensidade da força aplicada pelo empregado sobre o

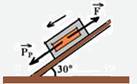
 F  — intensidade da força aplicada pelo empregado sobre o balcão fazendo-o descer com velocidade constante, ou seja, está em equilíbrio estático (F_R=0)  —  assim, F=P_P=1.000 N  —

R- E

16- a) A mola inteira (mola equivalente) tem constante elástica k’=12N/m e, nela, as três partes estão associadas em série, sendo que 1/k’= 1/k + 1/k +1/k, onde k é a constante elástica de cada parte.

1/k’=3/k  —  1/12 = 3/k  —  k =36N/m (constante elástica de cada parte da mola).

b) Paralelo (figura 2)  —  k­_e=36 + 36 +36  —  k_e=108N/m  —  período de oscilação – T=2π√(m/k_e)  —  T=2π√(0,1/108)  —  T=2π√9,26  — T=2π.0,03  —  T=6.10^-2π s  

c) Série  —  k_e=12N/m  —  T=2π√(m/k_e)  —  T=2π√(0,1/12)  —  T=2π√(0,008)  —  T=2π.0,09  —  T=18.10^-2π s      

 

Voltar para os exercícios