Aplicações das leis de Newton com atrito – Resolução

Resolução Comentada

Aplicações das leis de Newton com atrito

01- A velocidade do surfista se torna constante a partir de t=10s quando y≈330m (do enunciado e do gráfico)  —  a partir daí, ele percorre ∆S≈535- 330=205m, num intervalo de tempo ∆t=14 – 10=4s  —  nesse intervalo de tempo, sua velocidade é constante e

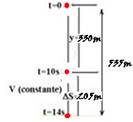
vale  —  V= ∆S/∆t =205/4  —  V ≈ 51,25 m/s  (velocidade com que ele chega ao solo, que é a velocidade limite)  —  do enunciado a força de resistência do ar é fornecida pela expressão  —  R=K.V²  —  quando ele atinge a velocidade limite, ele deixa de acelerar e, nesse instante, sua velocidade se torna constante sendo que a condição para que isso ocorra é que as intensidades da força de resistência do ar (vertical e para cima) se iguale à intensidade da força peso (vertical e para baixo)  —R=P=m.g=75.10=750N  —  750=K.(50)²  —  K=0,3Ns²/m²  —  R- A

02- As membranas interdigitais das patas funcionam como pára-quedas aumentando a força de resistência do ar (devido ao aumento da área de contato com o ar)  —   chega um momento em que a intensidade da força de resistência do ar  fica igual à intensidade da força peso  e ele entra em equilíbrio dinâmico (força resultante nula ) e sua velocidade vertical, nesse instante, é chamada velocidade terminal ou velocidade limite  —  essa velocidade permanece constante até ele chegar ao solo  —  R- A

03- Nas figuras abaixo P_p é a intensidade da parcela do peso que é responsável pela tendência de descida do bloco e F_at é a intensidade da força de atrito  —  como P_p=Psen30^o e F_at=μPcos30^o eles são os mesmos nas duas situações (fig.1 e fig. 2). 

Figura 1  —  P_p=mgsen30^o=5.10.0,5  —  P_p=25N  —  comparando V=V_o + a.t com V=2,0.t, você conclui que V_o=0 e a=2m/s²

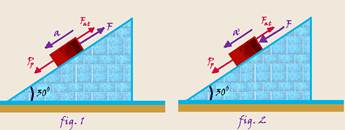
Aplicando a lei fundamental da dinâmica com a aceleração para baixo  —  F_R=m.a  —  (P_p –F – F_at)=ma  —  25 – F – F_at=5.2  —  F + F_at=15 (I)  —  figura 2  —  P_p=25N  —  comparando V=V_o + a’t com V=3,0.t você conclui que V_o=0 e a’=3m/s². 

Aplicando a segunda lei da dinâmica com a aceleração para baixo  —  F_R=ma’  —  (25 + F – F_at)=5.3  —  F = F_at – 10 (II)  —  substituindo (II) em (I)  —  F_at – 10 + F_at =15  —  2F_at=25  —  F_at=12,5N  —  F + F_at=15  —  F + 12,5=15  —  F= 2,5N  —  F_at=μmgcos30^o  —  12,5=.μ5.10.√3/2  —  μ=12,5/25√3  —  μ=1/2√3  —  μ≈0,29  —  R- C

04- A intensidade da força de atrito estático entre as caixa e a carroceria vale F_ate=μN  —  F_ate=μP  —  F_ate=μmg  —  F_ate=0,1.500.10  —  F_ate=500N (acima desse valor as caixas se movem).

  No movimento acelerado  —  V=Vo + a.t  —  30=0 + a.20  —  a=1,5m/s²   —  F_R=m.a  —  F_R=500.1,5  —  F_R=750N ( como F_R>F_ate, as caixas se movem para trás e ficam juntas na parte traseira do caminhão).

No movimento uniforme, elas estão em equilíbrio dinâmico e F_R=0. Assim, elas não se movem e ficam juntas na parte traseira.

No movimento retardado  —  V=Vo + a.t  —  0=30 – a.40  —  a=3/4m/s²  —  F_R=m.a  —  F_R=500.3/4  —  F_R=375N (menor que 500N, portanto elas não se movem e ficam na parte traseira do caminhão)  — R- A

05- A força de atrito devido aos pneus independe da largura (área de contato dos mesmos com o solo)  —  o aerofólio, que funciona como uma asa de avião invertida, comprime o carro contra o solo aumentando a intensidade da força normal  que o carro troca com o solo, aumentando assim a intensidade da força de atrito, pois F_at=μN  —  R- C

Observação: Além do aerofólio, o formato do carro também influi na compressão do carro contra o solo (veja figura), aumentando

ainda mais a força de atrito fazendo com que o carro efetue curvas com velocidades maiores.

06- No equilíbrio estático o corpo está na iminência de movimento  —  a força de atrito estático é

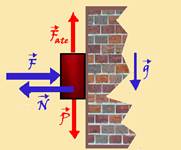
dada por F_ate=μ_eN, e se equilibra com o peso P, ou seja, F_ate=P  —  na situação do exercício, a força normal N é tal que N = F  —  assim, μ_eN = P  —  μ_eF=P  —  μ_e = P/F  —  o fato de μ_e < 1 implica que  P/F<1  —  0 < P < F  —  R- A

07- Colocando todas as forças que se relacionam com a pessoa, a parede e o solo.

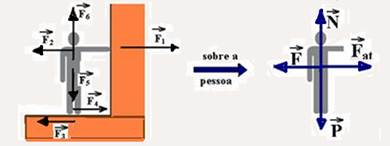
 F₁ e F₂  —  forças trocadas entre a pessoa e a parede de intensidade 120N  —   F₃ e F₄  —   forças de atrito trocadas entre os pés da pessoa e o solo  —  F₅  —  peso da pessoa trocada com o centro da Terra  —  F₆, força normal que a pessoa troca com o solo. 

Como a pessoa está em repouso, a força resultante sobre ela é nula e as forças verticais e horizontais se anulam  —  R- D

08- Como F_at=μN, e como μ é constante, a força de atrito é diretamente proporcional à intensidade da força normal (trocada entre a caixa e o solo)  —  quanto menor N, menor será as força que a caixa troca com o solo, tornando-a mais “leve” e consequentemente menor a força de atrito — das alternativas, a única força capaz de diminuir a  força de compressão N da caixa com o chão é a C  — R- C

09- Colocando as forças e decompondo em  e 

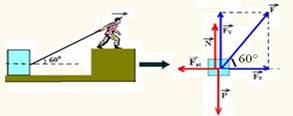
 P=mg=42.10  —  P=420N  —  F_X=Fcos60^o=F.0,5  —  F_X=0,5F  —  F_Y=Fsen60^o=F.√3/2  —  F_Y=0,85F.

 No equilíbrio estático temos, na horizontal F_at=F_X e na vertical, P=N + F_Y  —  N=P – F_Y  —  F_at=F_X  —  μN=0,5F  —  μ(P – F_Y)=0,5F  —  0,4(420 – 0,85F)=0,5F  —  168 – 0,34F=0,5F  —  0,84F=168  —  F=200N (qualquer valor acima de 200N desloca o bloco)  —   R- C

10- Vamos chamar de L’, comprimento total do pano e de L’ – L o comprimento da parte pendente  —  como o pano é de constituição homogênea, sua densidade é a mesma.

d=m_t/V_t  —  d (densidade) – m_t (massa total) – V_t (volume total)  —  m_t=d.V_t  —  m_t=d.(A.L’), sendo A (área se seção transversal, espessura do pano) e L’ (comprimento total do pano)  —  massa apoiada 

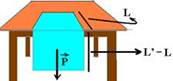
– m_a=d.A.L e massa pendente – m_p=d.A.(L’ – L)  — 

– peso da parte pendente  —  P=m_pg (m_p, massa da parte pendente)  —  a força de atrito entre o pano de comprimento L e a mesa está segurando o peso da parte pendente de comprimento (L’ – L), ou seja, F_at=P  —  μm_ag= m_pg  —  μ.d.A.L.g=d.A.(L’ – L).g  —   0,5.L=(60 – L)  —  1,5L=60  —  L=40cm  —   R- A

11- A força de atrito pode servir como força motora no deslocamento de um veículo  —  observe a

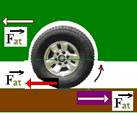
figura  —  se você quiser acelerar o carro para a esquerda, o motor do mesmo deve fazer o eixo e consequentemente a roda girar no sentido anti-horário  —  o pneu empurra o solo para trás () e o solo reage sobre o pneu e consequentemente sobre o carro (), movendo-o para a esquerda  —

em rodas com tração a força de atrito sobre o móvel é a favor do movimento e, em rodas sem tração, é contrária ao movimento  — R- B

12-  Dados: m = 120 kg; g = 10 m/s²; m = 0,8; F/A= 30 N/cm²; N = P = 1.200 N  —  para colocar a caixa em movimento o operador tem que vencer a força de atrito  —  F_operário = F_at = μN=0,8 (1.200) = 960 N  —  como ele está usando os dois braços, cada braço aplica então  —   F = F_operário/2=480 N  —  F/A=30  —  480/A=30  —  A=16cm²  —  uma das proteínas responsáveis pela contração das miofibrilas é a actina  —  R- A

13- Dados  —  g = 10 m/s²  —   μ_e = 0,60  —   μ_c = 0,80  —   m = 1.200 kg  —   força que a pista exerce no veículo tem duas componentes  —  normal   e  atrito    —  supondo que a frenagem ocorra em pista horizontal, a componente normal  da força que a pista aplica no veículo tem intensidade igual à do seu peso   —  N = P = m g = 12.000 N  —   componente de atrito estático máxima  —   F_atmax= μ_eN = 0,8 (12.000)  —    F_atmax = 9.600 N  —  a componente de atrito cinético: F_atc  = μ_c N = 0,6. (12.000)  —   F_atc = 7.200 N  —  R- D       

Observações: As figuras abaixo ilustram algumas das utilidades dos freios ABS

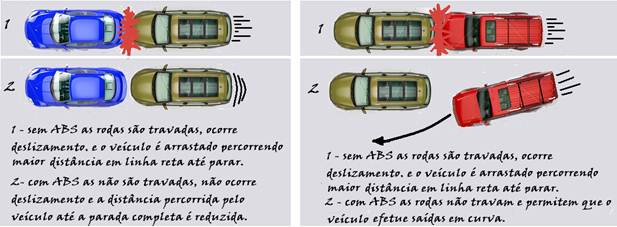
14- A força de tração que a corda aplica nas mãos da garota é a força que está puxando-as para a esquerda  —  a força de atrito é paralela ao apoio horizontal e para a direita, pois é sempre contrário ao movimento ou à sua tendência  —  R- E

 

Voltar para os exercícios