EQUIPOTENTIAL SURFACES – RESOLUTION
Commented resolution of entrance exam exercises on
Equipotential Surfaces – Work of the Electrostatic Force
01- I and II are true (see theory) and III is false because the electric field vector varies inversely with the square of the distance from the point to the charge — R- C
02- Observe the following expression — W=qU — U=W/q — R- D
03- All points on the trajectory AB are equidistant from the center of the charge and consequently constitute an equipotential surface — V A = V B — W=q.(V A – V B )=q.0 — W=0 — the work of the electric force in this displacement is zero.
04- The lines of force (solid lines) leave the positive charges and reach the negative ones and are perpendicular to the equipotential surfaces (dashed lines) — R- E
05- Along the same equipotential surface, the potential is always the same and the potential difference is zero and, consequently, the work is also zero.
06- False — the potential decreases I.
False — II. the lines are perpendicular
False — III. the surfaces are flat and parallel
R- And
07- a) U=Ed — (100 – 50)=5.10 2 .d — d=50/5.10 2 — d=1,0.10 -1 m
b) W AB =q(V A – V B )=2.10 -6 (100 – 50) — W AB =10 2 .10 -6 — W AB =1.0.10 -4 J
08- Since the initial (A) and final (D) positions are coincident, the work along the three trajectories is the same, since for conservative forces such as the electric force, the work is independent of the trajectory and depends only on the final and initial positions — R- B
09- W AB =q(V A – V B )=2.10 -6 (5 – 3) — W AB =4.10 -6 J — R- A
10- W=q(V A – V B ) — note that the largest ddp (V A – V B ) is that of the trajectory V — R- E
11- U=(V A – V B ) — V A <V B — U<0 — W=qU=-e(-Ed) — W=eEd — or — the positive plate is on the left (field moving away from it) and the electron moves spontaneously from A to B (spontaneous displacement, positive W) — R- B
12- a) False — it is null — A and B are on the same equipotential surface
b) Correct — they are on the same equipotential surface
c) False — it is the same in III and IV and is worth U AB = V A – V B = 100 – 80 = 20V
d) False – both are null
e) False — see c
R-B
13- R- B — see theory
14- Note that the potential of the upper plate is positive (it is connected to the positive pole of the generator) and that the potential difference U between the plates is
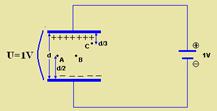
U=1V — V C >V A — A and B are on the same equipotential surface — V A =V B — W AB =q.(V A – V B )=q.0 — W AB =0 — d AC =d – (d/3 + d/2) — d AC =d/6 — U AC =V A – V C and since V C >V A , U AC is negative — U=Ed — 1=Ed — E=1/d —
W AC =qU AC =q.(-Ed AC ) — W AC =-q(1/d).d/6 — W AC = -q/6 — R- C
15- The work done on the charge Q depends on the potential difference between infinity and the point (a,0) — At infinity the potential
The electrical force of the system is zero and at point (a,0) it is also zero, since the two charges are in a symmetrical arrangement, with charges of the same module but opposite signs — thus, the work of the resulting force is zero.
16- W=qU=1,6.10 -19 .20 — W=32.10 -19 J — W AB =E CB – E CA — 32.10 -19 =E CB – 0 — E CB =3,2.10 -18 J —
R- And
17- E=F/q — 10 5 =F10 -6 — F=10 -1 N — F=ma — 10 -1 =10 -4 .a — a=10 3 ms 2 — Torricelli — V 2 =V o 2 + 2.a.ΔS —
0 2 =V o 2 + 2.(-10 3 ).2.10 -1 — V o =√4.10 2 — V o =20ms — R- B
18- a) U=Ed — 10 4 =E.10 -2 — E=10 6 V/m (N/C) b) E=F/q — 10 6 =F/1,6.10 -19 — F= 1.6.10 -13 N
c) F=ma — 1.6.10 -13 =9.10 -31 .a — a=0.17.10 18 m/s 2 — Torricelli — V 2 =V o 2 + 2.a.ΔS — V 2 =0 2 + 2.0,17.10 18 .10 -2 — V=√0,34.10 16 — V≈0.58.10 8 — V≈6.10 7 m/s
19- a) V A – V B =Ed — V A – 0=130.d — V 1 =130.1=130V — V 2 =130.2=260V and so on
b) Since the earth’s charge is negative, this body must have a negative charge for the electric force on it to be upward —
P=F — mg=qE — 1.3.10=q.130 — q=-0.1C — in practice, this would not be possible, since a small body could not be electrified with an electric charge of this order. The storm cloud, whose dimensions are enormous, can store electric charges of a few tens of coulombs.
20- Work as a change in kinetic energy — W AB = E CB – E CA = mV B 2 /2 – mV B 2 /2=2.10 -4 .6,400/2 – 2.10 -4 .400/2 — W AB =0.64 – 0.04 — W AB =0.6J — W AB =qU — 6.10 -1 =80.10 -6 .U — U=6.10 -1 /8.10 -5 =0.75.10 4 — U=7,500V — R- C
21- W AB =q(V A – V B )=2(1 – 3) — W AB =-4J — W BD =q(V B – V D )=1.5(3 – 7) — W BD =-6.0J — W DE =q(V D – V E )=1.(7 – 9) —
W total =-4 – 6 – 2 — W total =-12J — R- A
22- a) V A1 =KQ 1 /d 1 =9.10 9 .10 -9 /5.10 -2 — V A1 =180V — V A2 =KQ 2 /d 2 =9.10 9 .(-10 -9 )/4.10 – 2 — V A2 =-225V — V A =180 – 225 —
V A = -45V
b) V B =KQ 1 /d 1 + KQ 2 /d 2 =9.10 9 .10 -9 /5.10 -2 + 9.10 9 .(-10 -9 )/10.10 -2 — V B =180 – 90=90V — W AB =q(V A – V B )=2.10 -9 .(-45 – 90) — W AB = -2.7.10 -7 J
c) It decreases, because Q 3 moves away from the others and the electrostatic potential energy is inversely proportional to the distance.
23- a) Note that, where the potential V is zero, the two equipotential surfaces must cancel each other out (+150V with -150V, +200V
with -200V, etc.) according to the graph above.
b) Observe in the figure the coordinates of the distances from the center of the charges to point P — d A (0.02;0.03) and d B (0.08;0.03) —
d A 2 = (0.02) 2 + (0.03) 2 — d A =0.036m — d B 2 = (0.08) 2 + (0.03) 2 — d B =0.085m — E PA =V PA /d A =+250/0.036 — E PA =6.9.10 3 V/m — E PB =V PB /d B =-250/0.085 — E PB =3.0.10 3 V/m
w)
d) W PS =q(V P – V S )=2.10 -9 (0 – (+150 – 500)) — W PS =2.10 -9 .350 — W PS =7.0.10 -7 J
24-
25- a) E=F/q — 2.10 3 =F/3.10 -15 — F=6,0.10 -12 N
b) The distance you should consider is the distance between the two equipotential surfaces (vertical lines) that pass through A and B — d=4cm — U=(V A – V B )=Ed=2.10 3 .4.10 -2 — U=-80V (negative, since V A <V B ) — the variation in potential energy corresponds to the work — W=qU=3.10 -15 .(-80) — W=ΔE P =-2.4.10 -13 J
26- W=q(V A – V B )=1.(0 – 50) — W=-50J — W=E Cf – Eci=0 – mV o 2 /2 — -50=-4.10 -4 V o 2 /2 — V o =500m/s — R- B
27- This Coulomb force of attraction (radial direction, towards the center of the circumference “nucleus of the atom” and constant intensity), which acts on the electron and forces it to perform uniform circular motion is the resultant centripetal force and the work done by it is zero. This occurs because, as the speed module does not vary, the value of the kinetic energy does not vary either and as the work of the resultant force (which is centripetal) is equal to the variation of the kinetic energy W FR = W Fc = E CF – E Ci = 0, work is zero. Or, Being W = F c .d.cosα, and having the displacement in the same direction and same sense as , that is, it is
perpendicular to
28- V A =KQ/d A =9.10 9 .1,2.10 -8 /4.10 -1 — V A =270V — V B =KQ/d B =9.10 9 .1,2.10 -8 /6.10 -1 — V B =540V — W AB =q(V A – V B ) —
W AB =10 -6 (270 – 540) — W AB =-270.10 -6 =-2.7.10 -4 J — R- C
29-
30- – 62μJ, since the work does not depend on the trajectory.
31- V=KQ/d — note that KQ is constant, varying V and d — let’s assume the value of KQ as 40
in SI — 20=40/d 1 —d 1 =2m — 18=40/d 2 — d 2 =2.22m — 16=40/d 3 — d 3 =2.5m — 14=40/d 4 — d 4 =2.86m — R- B
32- In this case the resulting centripetal force F C = mV 2 /r is equal to the force of attraction between the two electric charges F=KQq/r 2 — mV 2 /=KQq/r 2 — V=√(KQq)/(mr) — R- A
33- The electric field vector is always tangent at each point to the field lines (of force) and
oriented from positive to negative charges — R- A
34- (V A – V B )=Ed — 100 – V B =10 3 .20.10 -2 — V B =-100V — R- B
35- E=F/q — 10 5 =F/10 -6 — F=10 -1 N — P=mg=0.1.10 — P=1N — maximum F + P=ma — 1.1=0.1 .a — a=11m/s 2 — minimum — P – F=ma — 1.0 – 0.1=0.1.a — a=9N — R- D
36- See in MHS (fisicaevestibular.com.br) that the period of a simple pendulum under the action of only
of the gravitational force (figure I) is given by T=2π√(Lm)/(P) — considering the electric and gravitational fields (figure II) the expression will be — T=2π√(Lm)/(P + F e ) — T=2π√(Lm)/(mg + qE) — R- E
37- a) False — it moves away from positive charges and approaches negative charges.
b) Correct — U 1 = E 1 d — 55.10 -3 = E 1 .7.10 -9 — E 1 = 7.857.10 6 V/m — U 2 = E 2 d — 100.10 -3 = E 2 .7.10 -9 — E 2 =14.285.10 6 V/m
c) False — it is uniform and nonzero
d) False — positive plates have higher potential
e) False — the equipotential surfaces inside the membrane have their potential decreased in the direction from the positive plates to the negative plates.
R-B
38- Kq 1 /d 1 + Kq 2 /(6 – d 1 )=0 — K.1/d 1 – K.2/(6 – d 1 )=0 — d 1 =2m — potential is zero at 2m of d 1 , or
that is, at points x=-4m and x=4m and, at all points that constitute a sphere of radius 4m (equipotential surface) — R- A
39- Calculation of the acceleration of the proton — V 2 = v o 2 + 2aΔS — 0 2 =(4.10 5 ) 2 +2.a.3.10 -2 — a=-16.10 10 /6.10 -2 — a=-8/3.10 12 m/s 2 —
F=ma — F=1,8.10 -27 .8/3.10 12 — F=4,8.10 -15 N — E=F/q=4,8.10 -15 /1,6.10 -19 — E=3.10 4 N/ C (V/m) —
RD
40- Data — distance between surfaces: d AB = 0.3 m — potential difference between surfaces — U AB = (500 – 200) = 300 V — proton charge: q = e — observe the figure that shows the lines of force, always perpendicular to the equipotential surfaces, and the direction of the electric field vector, the same as the lines of force — calculation of the intensity of the field vector
E d AB = U AB — E =U AB / d AB = 300/0.3 — E=1,000V/m — in the direction of the electric field vector, the electric potential is decreasing and to the right, as indicated in the figure — the minimum work of an external agent to take the proton from A to B occurs when it arrives at B with zero velocity, that is, the variation in kinetic energy is zero — by the kinetic energy theorem, the sum of the works is equal to the variation in kinetic energy — disregarding gravitational actions, only the electric force and this external force perform work — —
41- Kinetic Energy Theorem — W Fel = DE cin — (V A – V B ) q = mV 2 /2 — V=√2(V A – V B )q/m — V=√2.(300 – 100).
4.10 -5 /10 -3 — V=√16=4m/s — R- A
42- a) Considering the conservative system, the energies involved and their transformations are: electric potential energy, kinetic energy and elastic potential energy — when sphere 2 is released, the electric potential energy of the spheres decreases, transforming into kinetic energy for sphere 2 — when it collides with the object, the kinetic energy of this sphere is divided with the object — then, the kinetic energy of the sphere 2 – object set is transformed into elastic potential energy, stored by the spring — as the support plane is horizontal, the gravitational potential energy remains constant.
b) Data — Q 1 = Q 2 = Q; d 1 = d 3 = d; d 2 = 2d and m 1 = m 2 = m — the spring constant is K and the electrical permittivity of the medium is e o — the elastic potential energy stored in the spring in the final situation corresponds to the difference between the energies
43- Observe the figure below — applying Pythagoras to triangle ABC — a 2 = b 2 + c 2 — a 2 = (2√3) 2 +
2 2 — a=4cm — a=4.10 -2 m
— calculating the electric potential (V) at points A and B due to the charges present at C and D —
ignoring the action of other forces, the electric force is the resulting force — applying the kinetic energy theorem between points A and B — W AB =ΔE c — q(V A – V B )=mV B 2 /2 – mV A 2 /2 — -mV A 2 /2=q(V A – V B ) — V A =√-2q(V A – V B )/m —
A- A
44- The electronvolt is a unit of energy — it is equivalent to the work of the electric force to accelerate a particle with a charge equal to the elementary charge (q = e = 1.6.10 -19 C) when subject to a potential difference of U = 1 volt (V) — in electrostatics, the expression for the work of the electric force is — W = qU = 1.6.10 -19 .1 — 1 eV = 1.6.10 -19 J — R- D
45- a) As the two ions form a mechanically isolated system (free from the action of external forces), the system’s momentum is conserved — for both situations shown — Q s1 = Q s2 — mV o + 0 = m(3V o /4) + mV —
V = V o – 3V o /4 — V = V o /4
46- I. Correct — the more concentrated the lines of force, the more intense the electric field.
II. False — in the direction of the lines of force the electric potential is decreasing, therefore V D > V C .
III. False — negatively charged particles experience a force in the opposite direction to the electric field vector, moving spontaneously to regions of greater electric potential.
IV. Correct — positively charged particles move spontaneously in the same direction as the lower potentials, gaining kinetic energy and consequently decreasing their potential energy.
R-B
47- R- A — see that the particle is in dynamic equilibrium, that is, moving in a straight line at constant speed.
48- U=Ed — U=(F/q).d — U=mad/q — i=q/∆t — q=i. ∆t — U=mad/i.∆t — U=(kg).(m/s2).(m)/As — U=kg.m2/s3.A — R- B
49- Observe in the figure that the upper plate is electrified with positive charges (lack of electrons or excess of protons) and the lower one with negative charges (excess of electrons) — as the weight force is always vertical and downward, for there to be balance (zero resulting force) the electric force must be vertical and upward — for the electric force on the charge to be upward, the charge of the sphere must be negative (excess of electrons), since the upper positive plate attracts the charge and the lower negative plate repels it — F e = qE — P=mg=5.12.10 -4 .10 — P=5.12.10 -3 N — F e =P=5.12.10 -3 N — qE=5.12.10 -3 N — E=5.12.10 -3 /q —
U=Ed — 640=(5,12.10 -3 /q).2.10 -2 — q=10,24.10 -5 /6,4.10 2 =1,6.10 -7 C — q=ne — 1,6.10 -7 = n.1,6.10 -19 — n=1,0.10 12 electrons — R- A