Equipotential Surfaces – Work of the Electrostatic Force EN
EQUIPOTENTIAL SURFACES – WORK OF THE ELECTROSTATIC FORCE
Equipotential Surfaces – Work of the Electrostatic Force
The equipotential surface of an electric field is defined as any surface at whose points the electric potential is constant.
These surfaces have two important properties:
The electric force during the displacement of a point electric charge over an equipotential surface is zero.
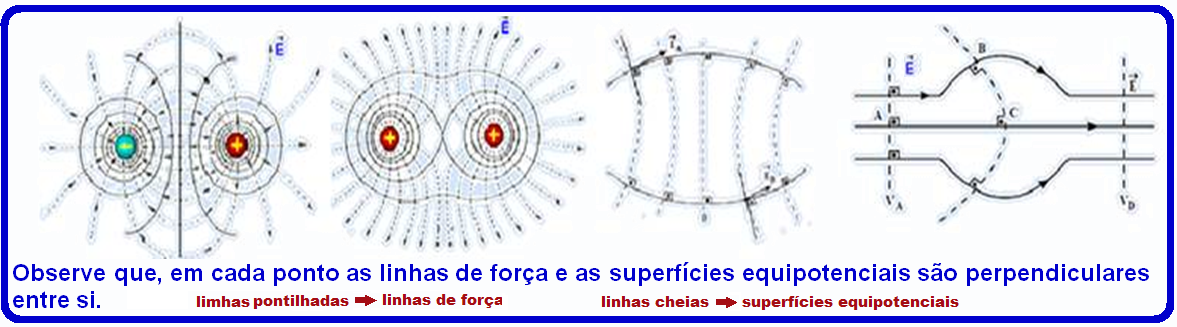
Equipotential surfaces are perpendicular to the lines of force or electric field lines and, consequently, perpendicular to the electric field vector. 
Equipotential surfaces and lines of force of a point charge Q
In the particular case of the field of a point charge Q , symmetry suggests that the equipotential surfaces are spherical surfaces concentric with the charge Q and the (field) lines of force are radial with the center of the charge.
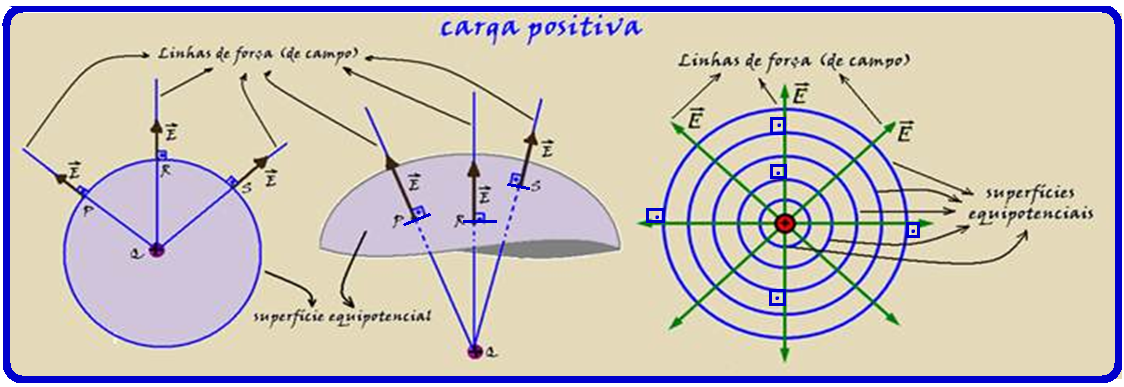
Note in the figures above that the lines of force (field) move away from the positive charges and in the figures below they move closer to the negative ones.
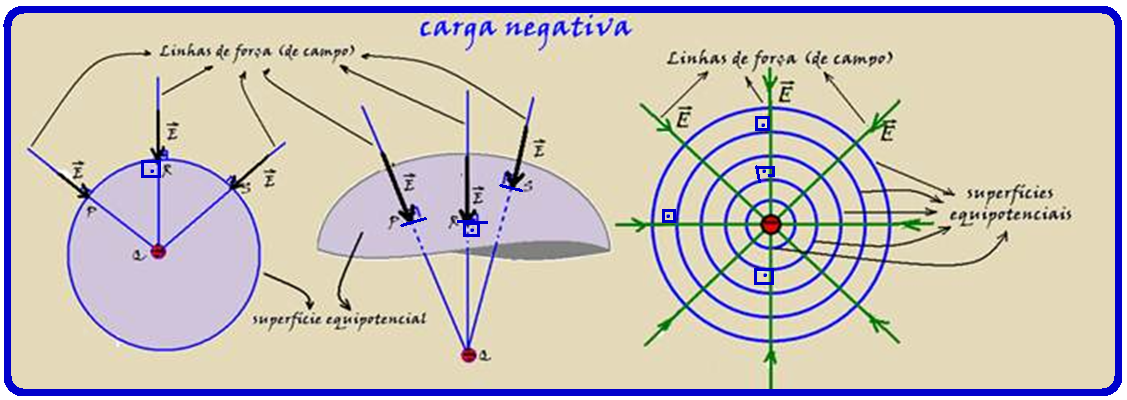
For positive charges, the potential of each surface increases as it approaches the charge and for negative charges it decreases as it moves away from the charge.
The figures below represent several configurations with their respective lines of force and equipotential surfaces.
Equipotential Surfaces of a Uniform Electric Field
A uniform electric field has the same intensity, direction and sense at all its infinite points and is obtained between two identical and parallel conductive plates electrified with charges of the same magnitude but opposite signs.
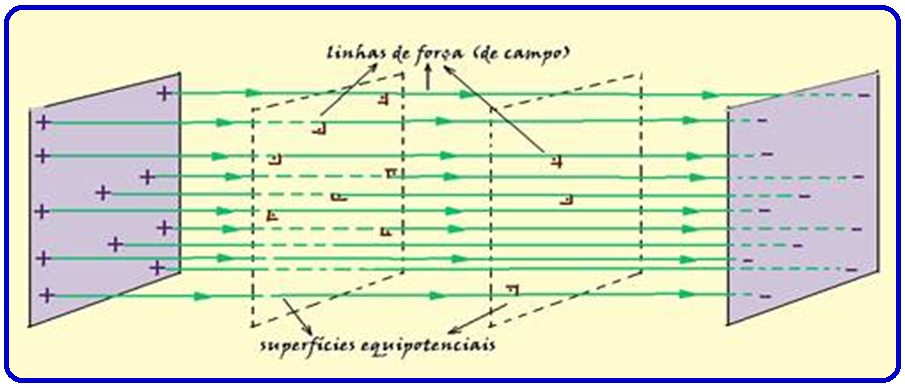
Note, in the figure above, that in this case the equipotential surfaces are flat and parallel to each other.
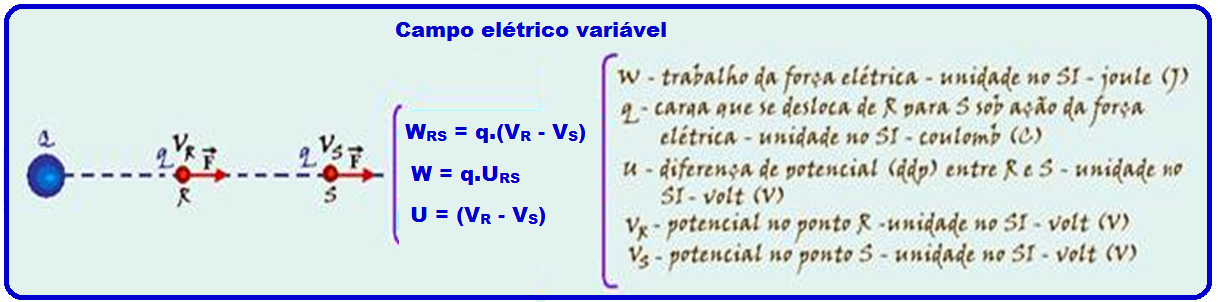
Work (W) and potential difference (U)
Consider the electric field created by a point source charge Q (figure I) and the uniform electric field created by two identical, parallel conductive plates electrified with charges of the same magnitude but opposite signs (figure II).
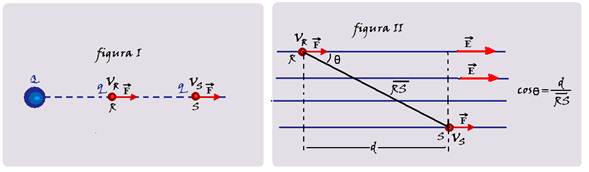
A test particle q, left inside these fields, is subject to a force , which makes it move from point R (with potential VR ) to point S (with potential V S ). 
Figure I variable electric field being the conservative force , the work done by it is provided by the variation of electric potential energy (initial minus final) W RS = E pR – E pS E pR = qV R E pS = qV S W RS = qV R – qV S W RS = q(V R – V S ) or W RS = qU RS, where
URS = V R – V S .
Figure II uniform electric field being the conservative force , the work done by it is provided by the variation of electric potential energy (initial minus final) W RS = E pR – E pS E pR q.V R E p q.V S W RS = qV R – qV S W RS = q(V R – V S ) or W RS = qU RS where U RS = V R – V S .
But, the work of the electric force is also provided by W RS = F.RS.cosθ = F.RS.d/RS W RS = Fd E=F/q F = qE W RS = qEd q(V R – V S ) = qEd (V R – V S ) = Ed or
URS = Ed .
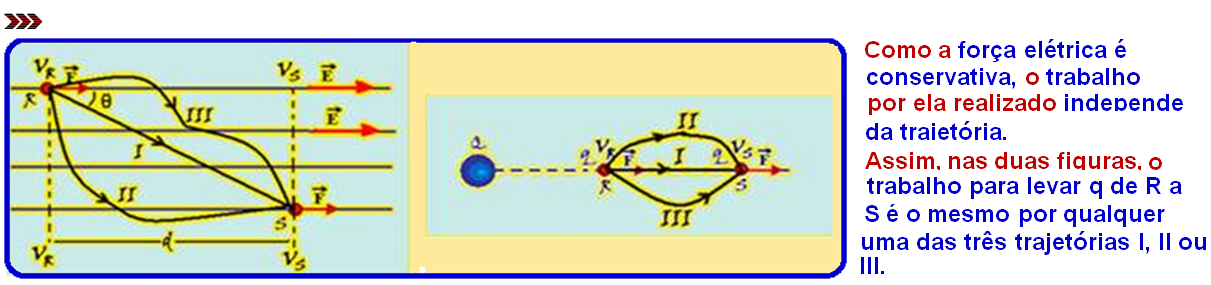
Look carefully at the form below with the expressions for the work W and the potential difference U of a variable electric field and a uniform electric field.
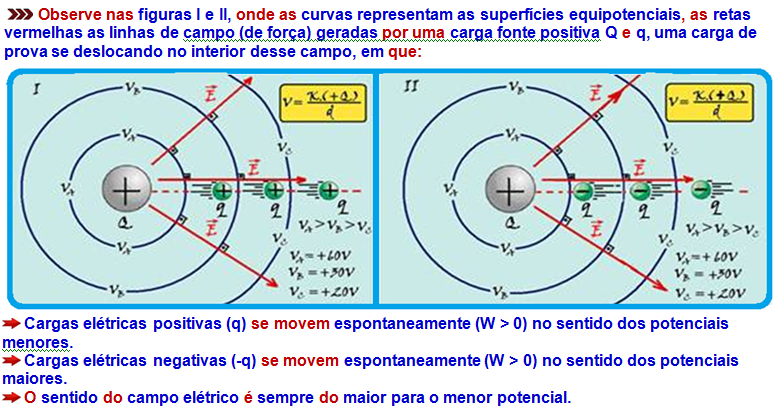
Observe in figures I and II, where the curves represent the equipotential surfaces , the red lines the field lines (of force) generated by a positive source charge Q and q, a test charge moving inside this field, in which:
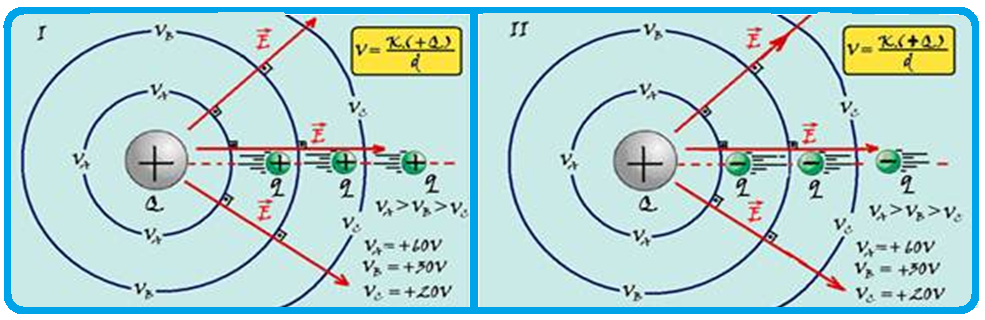
Positive electric charges (q) move spontaneously (W > 0) towards lower potentials.
Negative electric charges (-q) move spontaneously (W > 0) towards higher potentials.
The direction of the electric field is always from the highest to the lowest potential.
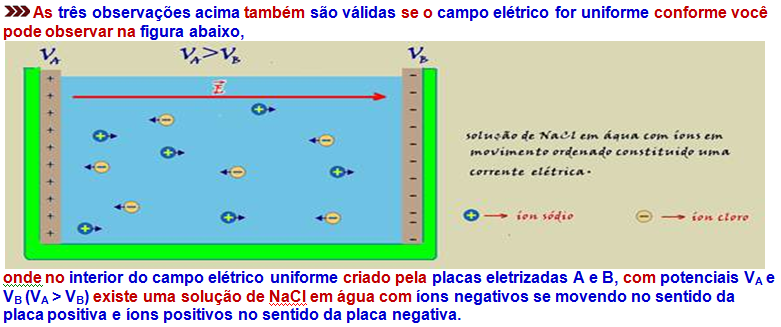
The three observations above are also valid if the electric field is uniform as you can see in the figure below,
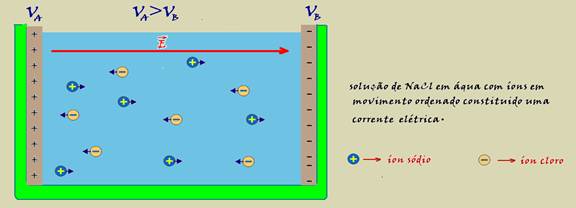
where inside the uniform electric field created by the electrified plates A and B, with potentials V A and V B (V A > V B ) there is a solution of NaCl in water with negative ions moving in the direction of the positive plate and positive ions in the direction of the negative plate.
Units of the electric field from the expression E=F/q, the field has SI units newton/Coulomb = N/C another unit from the expression U=Ed , the electric field has SI units volt/meter (V/m). 
Electron-volt (eV) corresponds to the work done when 1 electron left from rest at point A in an electric field moves spontaneously to point B, so that V A – V B = 1V W AB = q(V A – V B ) = 1.6.10 -19 .1 1 eV=1.6.10 -19 J.
By the expression W AB = q(V A – V B ), if points A and B are on the same equipotential surface (V A = V B = V), the work of the electric force in this displacement will be zero since W AB = q.(V – V) = q.0 = 0.
What you should know, information and tips
Equipotential surfaces and lines of force of a point charge Q
In the particular case of the field of a point charge Q , symmetry suggests that the equipotential surfaces are spherical surfaces concentric with the charge Q and the (field) lines of force are radial with the center of the charge.
Note in the figures above that the lines of force (field) move away from the positive charges and in the figures below they move closer to the negative ones.
For positive charges, the potential of each surface increases as it approaches the charge and for negative charges it decreases as it moves away from the charge.
The figures below represent several configurations with their respective lines of force and equipotential surfaces.
Units of the electric field from the expression E=F/q, the field has SI units newton/Coulomb = N/C another unit from the expression U=Ed , the electric field has SI units volt/meter (V/m). 
Electron-volt (eV) corresponds to the work done when 1 electron left from rest at point A in an electric field moves spontaneously to point B, so that V A – V B = 1V W AB = q(V A – V B ) = 1.6.10 -19 .1 1 eV=1.6.10 -19 J.
By the expression W AB = q(V A – V B ), if points A and B are on the same equipotential surface (V A = V B = V), the work of the electric force in this displacement will be zero since W AB = q.(V – V) = q.0 = 0.