Superfícies Equipotenciais – Trabalho da Força Eletrostática
Superfícies Equipotenciais – Trabalho da Força Eletrostática
Define-se superfície equipotencial de um campo elétrico a qualquer superfície em cujos pontos o potencial elétrico é constante.
Estas superfícies têm duas propriedades importantes:
![]() A força elétrica durante o deslocamento de uma carga elétrica puntiforme sobre uma superfície equipotencial é nula.
A força elétrica durante o deslocamento de uma carga elétrica puntiforme sobre uma superfície equipotencial é nula.
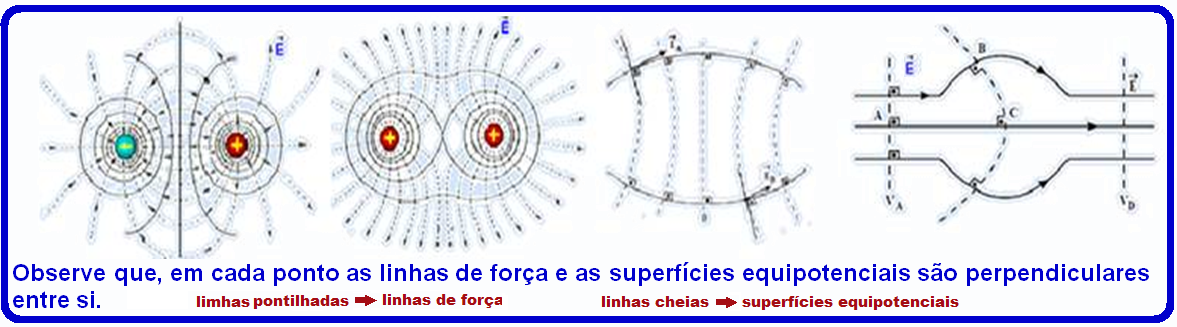
As superfícies equipotenciais são perpendiculares às linhas de força ou linhas de campo elétrico e, conseqüentemente, perpendiculares ao vetor campo elétrico ![]()
Superfícies equipotenciais e linhas de força de uma carga puntiforme Q
No caso particular do campo de uma carga puntiforme Q, a simetria sugere as superfícies equipotenciais são superfícies esféricas concêntricas com a carga Q e aslinhas de força (de campo) são radiais com o centro da carga.
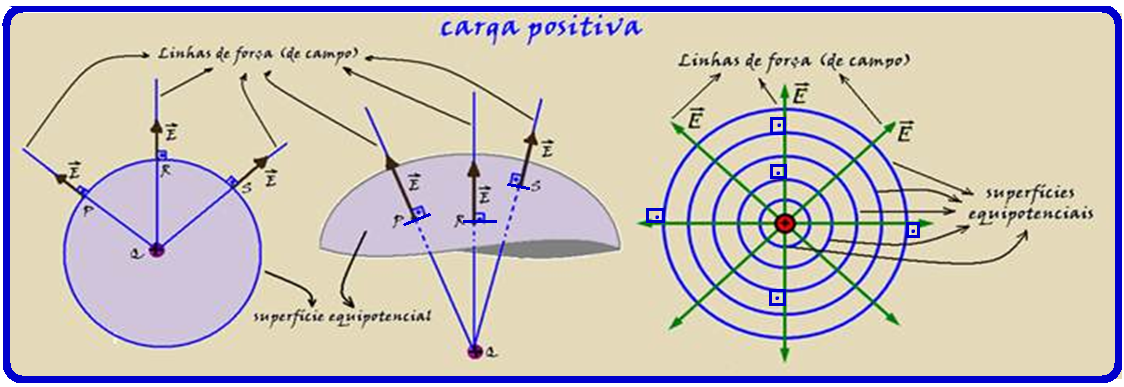
Observe nas figuras acima que as linhas de força (de campo) se afastam das cargas positivas e nas figuras abaixo se aproximam das negativas.
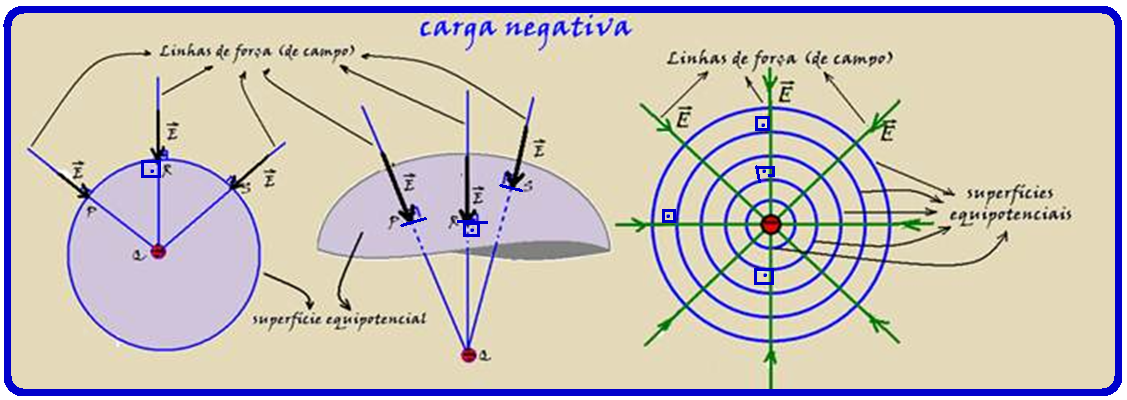
Para cargas positivas, o potencial de cada superfície aumenta quando se aproxima da carga e para cargas negativas diminui quando se afasta da carga.
Nas figuras abaixo estão representados várias configurações com as respectivas linhas de força e superfícies equipotenciais

Superfícies equipotenciais de um Campo Elétrico Uniforme
Um campo elétrico uniforme tem em todos os seus infinitos pontos mesma intensidade, mesma direção e mesmo sentido e é obtido entre duas placas condutoras idênticas e paralelas e eletrizadas com cargas de mesmo módulo, mas de sinais contrários.
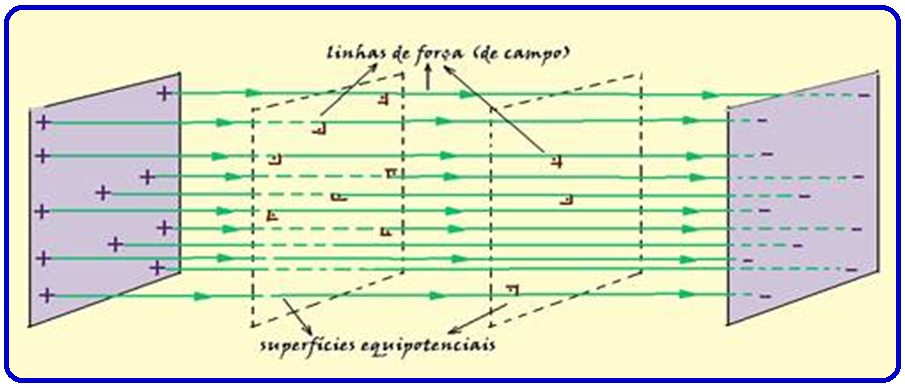
Observe, na figura acima, que nesse caso as superfícies equipotenciais são planas e paralelas entre si.
Trabalho (W) e diferença de potencial (U)
Considere o campo elétrico criado por uma carga fonte puntiforme Q (figura I) e o campo elétrico uniforme criado por duas placas condutoras idênticas e paralelas e eletrizadas com cargas de mesmo módulo, mas de sinais contrários (figura II).
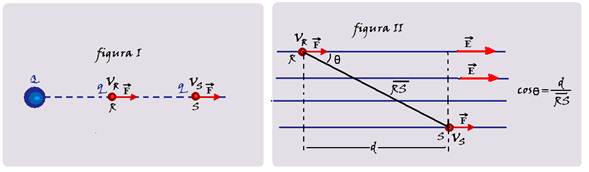
Uma partícula de prova q, abandonada no interior desses campos, fica sujeita a uma força ![]() , que a faz se deslocar do ponto R (de potencial VR) para o ponto S (de potencial VS).
, que a faz se deslocar do ponto R (de potencial VR) para o ponto S (de potencial VS).
Figura I ![]() campo elétrico variável
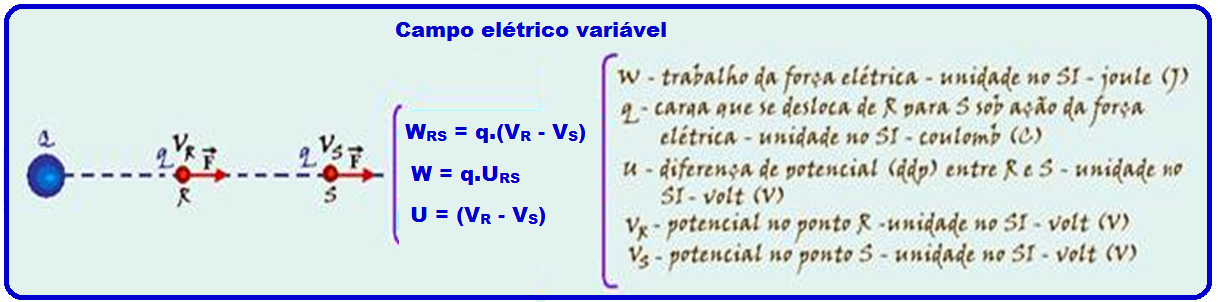
campo elétrico variável ![]() sendo a força
sendo a força ![]() conservativa, o trabalho por ela realizado é fornecido pela variação de energia potencial elétrica (inicial menos final)
conservativa, o trabalho por ela realizado é fornecido pela variação de energia potencial elétrica (inicial menos final) ![]() WRS= EpR – EpS
WRS= EpR – EpS ![]() EpR = q.VR
EpR = q.VR ![]() EpS = q.VS
EpS = q.VS ![]() WRS= qVR – qVS
WRS= qVR – qVS ![]() WRS= q(VR – VS) ou WRS = qURS, onde
WRS= q(VR – VS) ou WRS = qURS, onde
URS = VR – VS.
Figura II ![]() campo elétrico uniforme
campo elétrico uniforme ![]() sendo a força
sendo a força ![]() conservativa, o trabalho por ela realizado é fornecido pela variação de energia potencial elétrica (inicial menos final)
conservativa, o trabalho por ela realizado é fornecido pela variação de energia potencial elétrica (inicial menos final) ![]() WRS = EpR – EpS
WRS = EpR – EpS ![]() EpRq.VR
EpRq.VR ![]() Epq.VS
Epq.VS ![]() WRS = qVR – qVS
WRS = qVR – qVS ![]() WRS = q(VR – VS) ou WRS=qURS onde URS = VR – VS.
WRS = q(VR – VS) ou WRS=qURS onde URS = VR – VS.
Mas, o trabalho da força elétrica também é fornecido por ![]() WRS = F.RS.cosθ = F.RS.d/RS
WRS = F.RS.cosθ = F.RS.d/RS ![]() WRS = F.d
WRS = F.d ![]() E=F/q
E=F/q ![]() F = q.E
F = q.E ![]() WRS = q.E.d
WRS = q.E.d ![]() q(VR – VS) = q.E.d
q(VR – VS) = q.E.d ![]() (VR – VS) = E.d ou
(VR – VS) = E.d ou
URS = E.d.
Observe atentamente o formulário abaixo com as expressões do trabalho W e da diferença de potencial U de um campo elétrico variável e de um campo elétrico uniforme

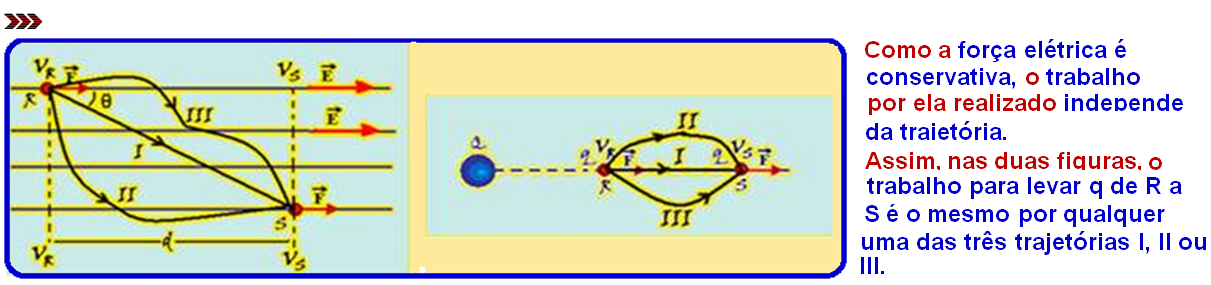
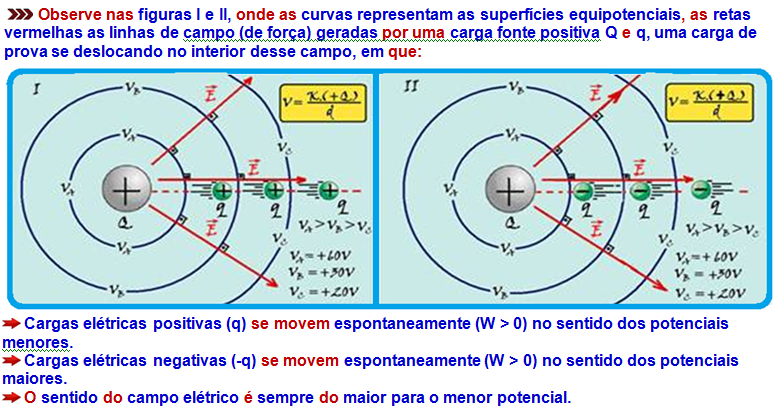
![]() Observe nas figuras I e II, onde as curvas representam as superfícies equipotenciais, as retas vermelhas as linhas de campo (de força) geradas por uma carga fonte positiva Q e q, uma carga de prova se deslocando no interior desse campo, em que:
Observe nas figuras I e II, onde as curvas representam as superfícies equipotenciais, as retas vermelhas as linhas de campo (de força) geradas por uma carga fonte positiva Q e q, uma carga de prova se deslocando no interior desse campo, em que:
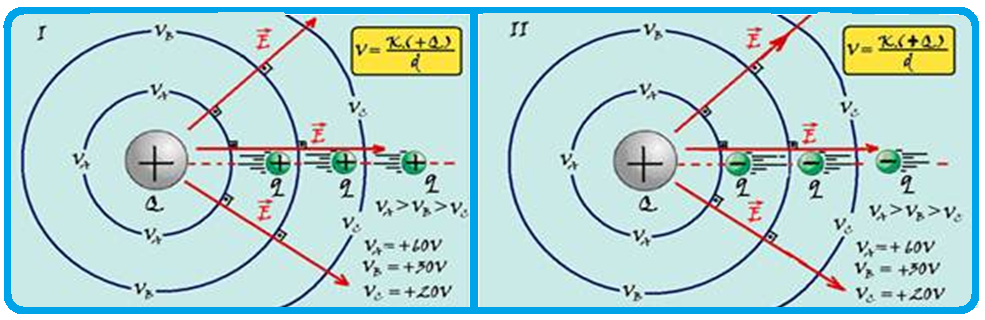
Cargas elétricas positivas (q) se movem espontaneamente (W > 0) no sentido dos potenciais menores.
Cargas elétricas negativas (-q) se movem espontaneamente (W > 0) no sentido dos potenciais maiores.
O sentido do campo elétrico é sempre do maior para o menor potencial.
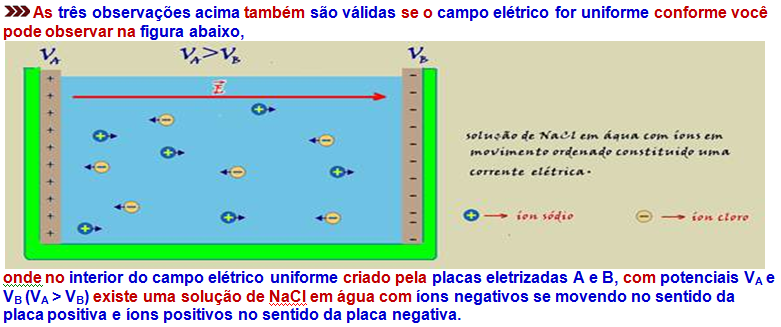
As três observações acima também são válidas se o campo elétrico for uniforme conforme você pode observar na figura abaixo,
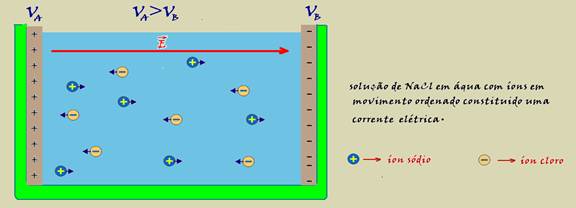
onde no interior do campo elétrico uniforme criado pela placas eletrizadas A e B, com potenciais VA e VB (VA > VB) existe uma solução de NaCl em água com íons negativos se movendo no sentido da placa positiva e íons positivos no sentido da placa negativa.
Unidades do campo elétrico ![]() da expressão E=F/q, o campo tem unidades no SI
da expressão E=F/q, o campo tem unidades no SI ![]() newton/Coulomb = N/C
newton/Coulomb = N/C ![]() outra unidade
outra unidade ![]() da expressão U=E.d, o campo elétrico tem unidades no SI
da expressão U=E.d, o campo elétrico tem unidades no SI ![]() volt/metro (V/m).
volt/metro (V/m).
Elétron-volt (eV) ![]() corresponde ao trabalho realizado, quando 1 elétron abandonado do repouso em um ponto A de um campo elétrico, desloca-se espontaneamente até um ponto B, de modo que VA – VB = 1V
corresponde ao trabalho realizado, quando 1 elétron abandonado do repouso em um ponto A de um campo elétrico, desloca-se espontaneamente até um ponto B, de modo que VA – VB = 1V ![]() WAB=q(VA – VB) = 1,6.10-19.1
WAB=q(VA – VB) = 1,6.10-19.1 ![]() 1 eV=1,6.10-19J.
1 eV=1,6.10-19J.
Pela expressão WAB = q(VA – VB), se os pontos A e B estiverem sobre a mesma superfície equipotencial (VA = VB = V), o trabalho da força elétrica nesse deslocamento será nulo pois, WAB = q.(V – V) = q.0 = 0.
O que você deve saber, informações e dicas
Superfícies equipotenciais e linhas de força de uma carga puntiforme Q
No caso particular do campo de uma carga puntiforme Q, a simetria sugere as superfícies equipotenciais são superfícies esféricas concêntricas com a carga Q e aslinhas de força (de campo) são radiais com o centro da carga.

Observe nas figuras acima que as linhas de força (de campo) se afastam das cargas positivas e nas figuras abaixo se aproximam das negativas.

![]() Para cargas positivas, o potencial de cada superfície aumenta quando se aproxima da carga e para cargas negativas diminui quando se afasta da carga.
Para cargas positivas, o potencial de cada superfície aumenta quando se aproxima da carga e para cargas negativas diminui quando se afasta da carga.
Nas figuras abaixo estão representados várias configurações com as respectivas linhas de força e superfícies equipotenciais


![]()



![]() Unidades do campo elétrico
Unidades do campo elétrico ![]() da expressão E=F/q, o campo tem unidades no SI
da expressão E=F/q, o campo tem unidades no SI ![]() newton/Coulomb = N/C
newton/Coulomb = N/C ![]() outra unidade
outra unidade ![]() da expressão U=E.d, o campo elétrico tem unidades no SI
da expressão U=E.d, o campo elétrico tem unidades no SI ![]() volt/metro (V/m).
volt/metro (V/m).
![]() Elétron-volt (eV)
Elétron-volt (eV) ![]() corresponde ao trabalho realizado, quando 1 elétron abandonado do repouso em um ponto A de um campo elétrico, desloca-se espontaneamente até um ponto B, de modo que VA – VB = 1V
corresponde ao trabalho realizado, quando 1 elétron abandonado do repouso em um ponto A de um campo elétrico, desloca-se espontaneamente até um ponto B, de modo que VA – VB = 1V ![]() WAB=q(VA – VB) = 1,6.10-19.1
WAB=q(VA – VB) = 1,6.10-19.1 ![]() 1 eV=1,6.10-19J.
1 eV=1,6.10-19J.
![]() Pela expressão WAB = q(VA – VB), se os pontos A e B estiverem sobre a mesma superfície equipotencial (VA = VB = V), o trabalho da força elétrica nesse deslocamento será nulo pois, WAB = q.(V – V) = q.0 = 0.
Pela expressão WAB = q(VA – VB), se os pontos A e B estiverem sobre a mesma superfície equipotencial (VA = VB = V), o trabalho da força elétrica nesse deslocamento será nulo pois, WAB = q.(V – V) = q.0 = 0.
