Linhas de força e Potencial eletrostático
Resolução comentada dos exercícios de vestibulares sobre
Linhas de força (campo) e Potencial eletrostático
01- R- A — veja teoria
02- R- C — veja teoria
03- a) Nas proximidades de q1, pois nela é maior a concentração de linhas de campo.
b) Como q1 é positiva (linhas de campo divergentes) e q2 negativa (linhas de campo convergentes), o sinal do produto q1.q2 é negativo.
04- R- D — veja teoria
05- a) Cargas positivas são fontes de campo elétrico enquanto cargas negativas são sorvedouros. Pela análise da figura, como as linhas de campo elétrico saem de B e chegam a A, conclui-se que A é negativa e B é positiva.
b) Da figura, percebemos que da carga B saem o dobro de linhas de campo que chegam na carga A, portanto: |QA| = 2|QB|.
c) Não. Pois caso fosse possível, haveria diferentes vetores ![]() em cada ponto de cruzamento das linhas de campo.
em cada ponto de cruzamento das linhas de campo.
06- Observe a figura abaixo, onde em cada espaço entre as placas foram colocados todos os
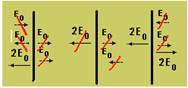
vetores, com as intensidades de cada placa, pois as placas são grandes.
R- E
07- (01) Verdadeira — veja figura abaixo
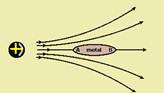
(02) Verdadeira — veja que na extremidade A existe maior concentração de linhas de campo
(04) Verdadeira — na extremidade A, nas cargas negativas a força é contrária ao campo
(08) Verdadeira — na extremidade B, nas cargas positivas campo e força tem mesma direção e mesmo sentido
(16) Verdadeira — a força de atração é maior que a força de repulsão
(32) Falsa — veja (04) e (08)
(64) Verdadeira — o campo elétrico é uniforme e consequentemente a força elétrica é constante.
R- (01 + 02 + 04 + 08 + 16 + 64)=95
08- R- B — veja teoria
09- Observe que na região do ponto 2 as linhas de campo elétrico são mais próximas — R- B
10- Saem da A e da C (positivas) e chegam a B (negativa) — R- E
11- I. Correta — Observe na figura abaixo que a carga da esquerda (positiva) produz num ponto P
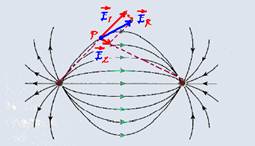
campo de afastamento (![]() ), a carga da direita (negativa) produz no mesmo ponto P uma campo de aproximação (
), a carga da direita (negativa) produz no mesmo ponto P uma campo de aproximação (![]() ) e a soma vetorial desses dois campos produz um vetor campo elétrico resultante (
) e a soma vetorial desses dois campos produz um vetor campo elétrico resultante (![]() ) que é tangente ao ponto.
) que é tangente ao ponto.
II. Correta — A quantidade de linhas de força (de campo) que saem das cargas positivas é a mesma das que chegam às negativas.
III. Falsa — a intensidade de cada campo independe da intensidade do outro (E=KQ/d2), e o campo resultante é a soma vetorial desses dois campos.
R- D
12- R- E — veja teoria
13- I. Falsa — é maior na região C onde a concentração de linhas de campo é maior.
II. Correta — quando a carga é negativa força e campo tem sentidos contrários.
III. Correta — quando a carga é positiva força e campo tem mesmo sentido.
R- D
14- Para que a gota atinja P ela deve ser desviada pela força elétrica para cima e, como a gota tem carga negativa o campo elétrico deve ter sentido contrário ao da força, ou seja, para baixo — R- A
15- R- C
16- V=Kq/d=9.109.(-10-6)/3,8.108 — V= -2,368.10-5V — R- C
17- a) Falsa — a carga Q é positiva e origina em P campo elétrico de afastamento e fornecido por E=KQ/d2.

b) Falsa — veja a anterior.
c) Correta — V=KQ/d=9.109.2.10-7/6.10-2 — V=3.104V
d) Falsa — veja a anterior
e) Falsa — veja a e c.
R- C
18- A em relação ao ∞ – UA∞=VA – V∞ — 150=VA – 0 — VA=150V — B em relação ao ∞ – UB∞=VB – V∞

— 100=VB – 0 —VB=100V — A em relação a B – UAB=VA – VB=150 – 100=50V ou A em relação a B com VB=0 — UAB=VA – VB —
50=VA – 0 — VA=50V — R- D
19- I. Falsa — potencial elétrico é grandeza escalar, não tem direção nem sentido.
II. Correta — observe que nos três casos o potencial em 0 vale Vtota=Kq/R + Kq/R + Kq/R — Vtotal=3Kq/R
III. Falsa — veja a anterior
R- B
20- O potencial no ponto 0, que é uma grandeza escalar é a soma algébrica do potencial em 0 originado pelos “n” prótons — V0=nKq/r — R- C
21- Um hexágono regular é composto por 6 triângulos equiláteros — VA=Kq/d + Kq/d + KQ/2d —
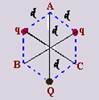
0=2Kq/d + KQ/2d — Q=-4q — R- D
22- a) Se os dois átomos devem ficar em equilíbrio, a resultante das outras forças internas deve anular a força elétrica entre as cargas — FR=Fe=KQ.q/d2=9.109.│1,6.10-19│ . │-1,6.10-19│/(2.10-10)2 — F=5,76.10-9N
b) O módulo da energia potencial elétrica associada ao sistema vale — Ep=Kq.q/d=9.109.│1,6.10-19│ . │-1,6.10-19│/(2.10-10) —
Ep=1,152.10-18J.
23- Para que essas cargas se aproximem é preciso que um agente externo aplique forças, forçando a aproximação, e fornecendo
energia ao sistema — R- A
24- V=KQ/d — 30=9.109Q/3.10-2 — Q=10-10C — R- D
25- V1=KQ/d=9.109.(-2,0.10-9)/1 — V1=-18V — V2=KQ/d=9.109.(-2,0.10-9)/2 — V2=-9V — U12=V1 – V2 =
(-18) – (-9) — U12=-9V — R- E
26- Ep=KQq/d — observe que se você dobrar cada carga Ep ficará quadruplicada e que se você multiplicar a distância por 4, Ep ficará 4 vezes menor — R- E
27- Ep+Q=K(+Q)/3a — Ep-Q=K(-Q)/a — Ep=+KQ/3a – KQ/a — Ep=(KQ – 3KQ)/3a — Ep=-2KQ/3a —
R- E
28- Observe na figura abaixo que o deslocamento da partícula é para a direita e é espontâneo,
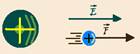
portanto a energia potencial eletrostática do sistema está diminuindo. A força faz surgir sobre a partícula uma aceleração, portanto sua velocidade e consequentemente sua energia cinética está aumentando — R- E
29- Observe que para que o potencial criado pelas duas cargas seja nula nos pontos, como elas tem mesmo módulo e sinais contrários, esses pontos devem ser eqüidistantes de cada carga — R- A
30- Os pontos devem estar eqüidistantes de Q — veja figura abaixo:
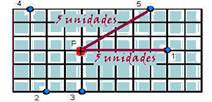
R- B
31- Lembre-se de que cargas positivas originam campos de afastamento e negativas, campos de aproximação — veja a figura —
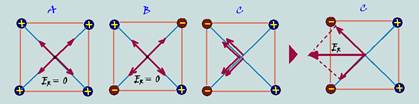
R- C
32- O potencial elétrico é uma grandeza escalar e, no centro do quadrado é a soma algébrica dos potenciais criados por cada carga

— A – EA=Kq/d + Kq/d + Kq/d + Kq/d=4Kq/d — B – EB= Kq/d + Kq/d – Kq/d – Kq/d=0 — C – EC= Kq/d + Kq/d – Kq/d – Kq/d=0 — R- D
33- Como a carga é positiva ela ficará sujeita a uma força que tem a mesma direção e sentido que o campo elétrico e intensidade
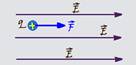
F=q.E, que a fará acelerar para a direita (figura) sujeita a uma aceleração a, aumentando sua velocidade e consequentemente sua energia cinética e diminuindo sua energia potencial elétrica de modo que sua energia mecânica seja constante (a força elétrica é conservativa) — R- 05
34- V=0=K.(+2q)/d1 + K(-q)/d2 — d1=2d2 — d2=1, d2=2 (K) — d2=3, d2=6 (L) — R- E
35- VA=0 — KQ/(104 – x) – K3Q/x=0 — 1/(104 – x) = 3/x — x=312/4 — x=78cm
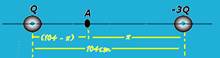
R- D
36- Situação inicial
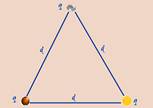
EP1=Kq2/d + Kq2/d + Kq2/d — Ep1=3kq2/d
Situação final
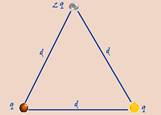
Ep2=Kq2/d + K(2q)2/d + K.(2q)2/d — Ep2=5Kq2/d — Ep2=(5/3)Ep1 — R- C
37- a) As duas cargas originam em x campos de afastamento que devem se anular — E1=Kq1/(6 – x)2 — E2=Kq2/x2 — E1=E2 —

K.4.10-5/(6 – x)2=K.10-5/x2 — 4/(6 – x)2=1x2 — x2/(6 – x)2=1/4 — x/(6 – x)=1/2 — x=6/3 — x=2 — o campo elétrico é nulo a 2m de q2 e a 4m de q1.= ou na posição x=4m
b) V=Kq1/3 + Kq2/3=9.109.4.10-5/3 + 9.109.10-5/3 — V=15,0.104V
c) E1=9.109.4.10-5/9=4.104N/C — E2=9.109.10-5/9=104N/C — ER=4.104 – 104 — ER=3.104N/C — E=F/q3 — 3.104=F/10-5 — F=3.10-1N — F=ma — 3.10-1=1ª — a=0,3m/s2.
38- E=KQ/d2 — 9.103=KQ/d2 — KQ=9.103d2 — V=KQ/d — 18.103=KQ/d — KQ=18.103d — 9.103d2=18.103d — d=2m — 18.103=9.109Q/2 — Q=36.103/9.109 — Q=4.10-6C ou Q=4μC
39- Quando x=0,6m – Ep=6.10-4J — V=Ep/Q — V=6.10-4/10-6 — V=6.102V
40- Todo ponto “aterrado” possui potencial nulo — na figura 2 — V1 + V3,1 + V2,1 = 0 — KQ1/a KQ/b + KQ/b=0 — Q1/a=-2Q/b — Q1=-2Qa/b — na figura 3 — KQ2/a + KQ1/b + KQ/b=0 — Q2/a=Q1/b – Q/b — substituindo Q1 — Q2/a=+2Qa/b2 – Q/b — Q2=Qa/b(2a/b – 1) — na figura 4 — KQ3/a + KQ1/b + KQ2/b=0 — Q3/a + Q1/b + q2/b=0 — usando as expressões de Q1 e Q2 — Q3/a=2Qa/b2 – Qa/b2(2a/b – 1) — Q3/a=Qa/b2(2 – 2a/b + 1) — Q3=Qa2(3 – 2a/b)
41- Como o sistema é simétrico quanto a energia potencial elétrica, o que ocorrerá é a transformação de energia potencial gravitacional em energia cinética — m.g.h = m.v2/2 — g.h = v2/2 — g.6 = v2/2 — v2 = 12g — v = √12g
42- A despolarização ocorre na fase em que o potencial sobe, que é a fase 0. A repolarização ocorre quando o potencial está voltando ao potencial de repouso, o que ocorre na fase 3.
R- B
43- Dados: Q3 = 1,44.10-4 C; k = 1,3.109 N.m2;C2.
Cálculo da distância (L) da carga Q3 ao ponto (0;0;c), que é o ponto (0;0;3), (figura).
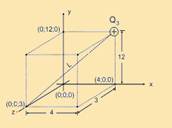
Aplicando Pitágoras — L2 = 42 + 32 + 122 — L2 = 169 — L = 13 m. — Calculando o potencial elétrico — V=KQ3/L=1,3.109.1,44.10-4/13 — V=14,4.103V — V=14,4kV — R- A
44-

R- A
45- Observe na figura abaixo as superfícies equipotenciais com as respectivas distâncias — V2=kQ/r2 (I) — V1=kQ/r1 (II) —
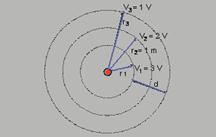
V3=kQ/r3 (III) — (II)/(I) — V1/V2=kQ/r1 x r2/kQ — r1=2/3m — r1=0,67m — (III)/(I) — V3V2=kQ/r3x r2/kQ — r3=2m —
Distância d pedida — d=r3 – r1=2,00 – 0,67 — d=1,33m
46- Dados — V = 600 V — E = 200 V/m — k = 9.109 N.m2/C2.
A carga Q é positiva, pois o potencial elétrico por ela gerado é positivo — potencial — V=kQ/r — E=kQ/r2 — V/E=kQ/r x r2/kQ — 600/200=r — r=3m — V=kQ/r — 600=9.109.Q/3 — Q=2,0.10-7C
47- I. Correta — quanto mais concentradas as linhas de força, mais intenso é o campo elétrico.
II. Falsa — no sentido das linhas de força o potencial elétrico é decrescente, portanto VD > VC.
III. Falsa — partículas com carga negativa sofrem força em sentido oposto ao do vetor campo elétrico, movimentando-se espontaneamente para regiões de maior potencial elétrico.
IV. Correta — partículas positivamente carregadas movimentam-se espontaneamente no mesmo sentido dos menores potenciais, ganhando energia cinética, consequentemente, diminuindo sua energia potencial.
R- B
48-Veja as características do potencial originado nesse caso: 
Do gráfico, quando d=0,15m, V=300V — V=k.Q/d — 300=9.109.Q/0,15 — Q=45/9.109 — Q=5.10-9C=5nC.
49– Num campo elétrico uniforme o vetor campo elétrico tem em todos os seus infinitos pontos mesma intensidade, mesma
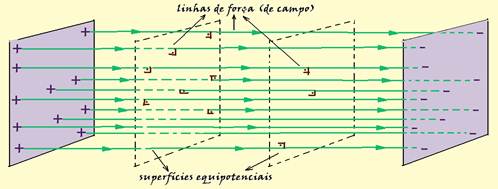
direção e mesmo sentido e é obtido entre duas placas condutoras idênticas e paralelas e eletrizadas com cargas de mesmo módulo, mas de sinais contrários — observe que nesse caso as superfícies equipotenciais (todos os seus pontos possuem o mesmo potencial elétrico) são planas e paralelas entre si — assim, os pontos A e C possuem o mesmo potencial elétrico (estão numa mesma superfície equipotencial) — observe também que o potencial diminui no sentido das linhas de força, que se afastam da placa positiva — R- C
50- Lembre-se de que o potencial elétrico diminui ao longo das linhas de força (de campo) — R- A — ou, do enunciado 0 < VA – VC — VA> VC — 0 < VB – VC — VB > VC — VA – VC < VB – VC — VA < VB — VC < VA < VB — R- A
51- Campo elétrico de intensidade E criado por uma carga de módulo Q a uma distância d dessa carga — E=k.Q/d2 (I) — potencial elétrico de intensidade V criado por uma carga de módulo Q a uma distância d dessa carga — V=k.Q/d (II) —
Dividindo (I) por (II) — (I)/(II) = E/V=(kQ/d2)x(d/kQ)=1d — E/V=1/d — V = E.d — 180=360.d — d=0,5m — substituindo d=0,5m em (II) — 180=9.109.Q/0,5 — Q=90/9.109 — Q=10.10-9=10nC —
R- E
52- Inicialmente você deve se lembrar que as linhas de força de um campo magnético são linhas fechadas e de um campo eletrostático são linhas abertas — A figura I mostra as linhas de força (de campo) de um campo elétrico (eletrostático) criado por uma placa plana, muito extensa e uniformemente eletrizada por cargas elétricas positivas (campos de afastamento) — a figura II sugere o campo eletrostático originado por duas cargas pontuais eletrizadas com cargas positivas (campo de afastamento), colocadas próximas uma da outra, mas pode representar também o campo magnético originado por dois pólos norte de imãs diferentes (linhas de indução saem dos pólos norte), quando colocados próximos (veja figura abaixo), apenas que, nesse caso as

linhas são fechadas (saem do pólo norte de cada imã e chegam ao pólo sul do mesmo imã) — a figura III representa campo magnético, pois são linhas fechadas — pode representar as linhas de indução de uma espira percorrida
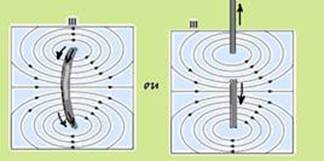
por corrente elétrica ou por dois fios retilíneos, percorridos por correntes elétricas de sentidos opostos (veja figuras acima) — a figura IV também mostra um campo magnético (linhas fechadas) — esse campo magnético é gerado por um fio retilíneo, perpendicular ao plano dessa folha, com a corrente elétrica saindo da mesma.
R- A ou E
