Resolução comentada dos exercícios de vestibulares sobre Força elétrica – Lei de Coulomb
Resolução comentada dos exercícios de vestibulares sobre
Força elétrica – Lei de Coulomb
01- F=KQq/d2=9.109.4.10-16.6.10-16/(3.10-9)2 — F=9.24.10-23/9.10-18 — F=24.10-5 N — R- D
02- F=KQq/d2 — 10-1=9.109.2.10-6.2.10-6/d2 — 10-1=36.10-3/d2 — d2=36.10-2 — d=6.10-1m — R- B
03- R- E — veja teoria
04- Q1=Q2=Q — F=KQq/d2 — 3,6.10-2=9.109.Q.Q/(1)2 — Q2=3,6.10-2/9.109=0,4.10-11 — Q2=4.10-12 — Q=2.10-6C — R- E
05- Observe na expressão F=KQq/d2 que a intensidade da força F é inversamente proporcional ao quadrado da distância — se a distância ficou 3 vezes maior, a força deverá ficar 33=9 vezes menor — 3,6.10-5/9 — F=0,4.10-5N — R-B
06- a) Observe na expressão F=KQq/d2 que a intensidade da força F é diretamente proporcional ao módulo de cada carga — se você triplicar o valor de uma das cargas a força elétrica ficará 3 vezes maior.
b) Observe na expressão F=KQq/d2 que a força F é inversamente proporcional ao quadrado da distância entre as cargas — se você duplicar a distância, a força elétrica ficará 22=4 vezes menor.
07- Observe que a força é de repulsão o que significa que as cargas têm mesmo sinal, ou seja, (+).(+)>0 e (-).(-)>0 — R- C
08- F1=Kq1.q2/r2 — F1>0 (q1 e q2 tem mesmo sinal) — -F2=K.q1.q3/(2r)2=(Kq1.q2/3)/4r2 — -F2=Kq1.q2/12r2 — F2<0 (q1 e q3tem sinais opostos) — F1/F2= Kq1.q2/r2 X 12r2/Kq1q2 — F1/F2=12 — R- (02 + 16)=18
09-
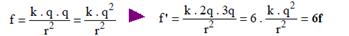
R- E
10- F=KQq/d2 — 720=9.109.Q.2Q/12 — Q2=720/18.109 — Q2=40.10-9 — Q=√(4.10-8) — Q=2.10-4C e Q’=4.10-4C
11- Força elétrica — Fe=KQq/d2 — força gravitacional — FG=GMm/d2 — igualando-as — KQq/d2 = GMm/d2 — KQ2/d2 = GM2/d2 — M2Q2=KG — MQ=√(KG) — R- C
12- Antes do contato — Fa=KQq/d2=KQ.9Q/d2 — Fa=9KQ2/d2 — após colocadas em contato e separadas cada uma fica com carga Q’ tal que Q’= (-Q + 9Q)/2 — Q’= 4Q — Fd=KQq/d2=K4Q.4Q(2d)2 — Fd=16KQ2/4d2 — Fd=4KQ2/d2 — Fd/Fa=4KQ2/d2 X d2/9KQ2 — Fd/Fa=4/9 — R- B
13- Quando r=3m — F=2,5.10-4N — F=KQq/r2 — 2,5.10-4=9.109.Q.Q/32 — Q2=2,5.10-13=25.10-14 — Q=5.10-7C — R- E
14- Observe que, como a carga de uma partícula dobrou, a força também dobrará (2F) e como a distância dobrou, a força ficará 4 vezes menor (2F/4=F/2) — F’=15/2 — F’=7,5N — R- B
15- Cada esfera ficará com cargas de sinais opostos e de módulo — Q=n.e=5.1014.1,6.10-19 — Q=8.10-5C — F=KQq/d2 — F=9.109.8.10-5.8.10-5/(8.10-2)2 — F=9.10-1/10-4 — F=9.103N — R- B
16- Observe as figuras abaixo:
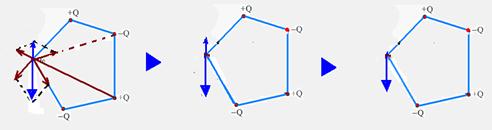
R- D
17-
R- E
18- Observe na figura abaixo que a carga –Q não pode estar à esquerda de Q e nem a direita de 4Q, pois nessas posições a
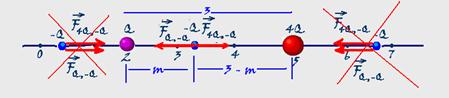
resultante não seria nula — ela tem que estar entre Q e 4Q na posição da figura — FQ,-Q=KQQ/m2 — F4Q,-Q=K4QQ/(3 – m)2 — KQQ/m2= K4QQ/(3 – m)2 — 1/m2=4/(3 – m)2 — (3 – m)2/m2=4 — (3 – m)/m=√4 — 2m=3 – m — m=1 — está na abscissa x=2 + 1=3 — R- C
19- a) A intensidade da força elétrica é igual à intensidade da força centrípeta — Fe=Fc — KQq/R2=mV2/R — V=√(KQq/mR)
b) V=2πR/T — 2πR/T=√(KQq/mR) — 4π2R2/T2 =KQq/mR — T2=4π2R2mR — T=2πR√(mR/KQq)
20- a) Ou as duas são positivas ou negativas
b) Ação de q1 e de q3 sobre q2 — Fq1q2=Kq1q2/r2 — Fq3q2=K.q3q2/r2 — Kq1q2/r2 = K.q3q2/r2 — q1=q3=q — ação de q2 e de q3 sobre q1 — Fq3q1=Kq2/(2r)2 — Fq2q1=KQ2q1/r2 — Kq2/(2r)2 = KQ2q1/r2 — q=4.2,7.10-4 — q=q1=q2=10,8.10-4C
c) Se você retirar um pouquinho a carga q2 da posição de equilíbrio, ela não retorna à mesma — equilíbrio instável.
21- Sendo as cargas elétricas idênticas, a força exercida por 3 sobre 2 deve ser 4 vezes maior que a força exercida por 1 sobre 2 (metade da distância) — F12=4.10-5N — F32=4.4.10-5 — F32=16.10-5N — FR=16.10-5 – 4.10-5 — FR=12.10-5N — R- C
22- A carga q’ deve estar entre as duas cargas a uma distância m de +q — F1=Kq’.q/m2 — se estiver à distância n de +4q — F2= Kq’.4q/m2 — F1 = F2 — Kq’.q/m2 = Kq’.4q/m2 — (n/m)2=4 — n=2m — n + m = 6 — m=2 — n=4 — R- B
23- Observe na figura abaixo que a carga pontual para ficar em equilíbrio não pode estar entre as cargas e que deve estar no ponto
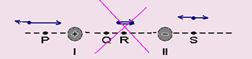
S, pois a carga positiva tem intensidade maior que a negativa — R- C
24- Observe que FAB é 9 vezes maior que FCB=3.10-6N (inversamente proporcional ao quadrado da distância) — FAB=9.3.10-6 —
FAB=27.10-6N — FR=27.10-6 – 3.10-6 — FR=24.10-6N — R- D
25-
R- E
26- Força elétrica — Fe=KQq/d2 — Força gravitacional — FG=GMm/d2 — quando a distância é 2km Fe=FG — KQq/22=GMm/22 — KQq=GMm — quando a distância é 5km as massas M e m e as cargas Q e q continuam iguais, então Fe continua igual a FG e as partículas continuam equilibradas — R- B
27- Veja esquema abaixo:
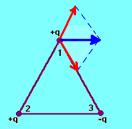
R- C
28- Força elétrica que 1 exerce em 3 — F13=Kq1.q3/d2=9.109.10-6.10-6/32 — F13=10-3N — como a distância e as cargas são as mesmas a força que 2 exerce em 3 também será a mesma — F23=10-3N=F13=F — a força que q1 exerce em q3 é de atração e a que q2 exerce em q3 é de repulsão (figura).
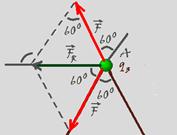
Observe que os triângulos são eqüiláteros, então a intensidade de FR será FR=F=10-3N,direção horizontal e sentido para esquerda.
29- a) Como elas estão no ar, com o tempo as esferas irão se descarregando e se aproximando — as forças que agem nas esferas, T intensidade da força de tração no fio, P intensidade da força peso e F força elétrica de repulsão entre as esferas com cargas de mesmo sinal, para qualquer posição das esferas tem sempre a mesma intensidade em ambos os fios e as decomposições dessas forças serão sempre simétricas,e os ângulos serão sempre iguais.
b) Colocando as forças que agem sobre uma das esferas e que são — 
– força de tração no fio — 
– força peso — 
– força
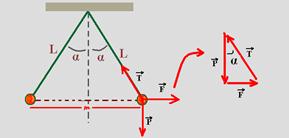
Elétrica — considerando m como a distância entre as duas cargas — senα=(m/2)/L — 0,6=m/2.0,09 — m=0,108m — no triângulo de forças — tgα=F/P — 0,75=F/P — F=0,75P — KQ.Q/m2=0,75.m.g — 9.109.Q2/(0,108)2=0,048.10 — Q=2,5.10-7 C
30- Observe na figura, onde todas as forças que agem sobre a carga Q acima, da direita foram
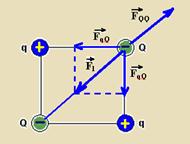
colocas, que, para que 
anule 
as cargas q e Q devem ter sinais opostos — 
=
+ — (F1)2 = (FqQ)2 + (FqQ)2 — (F1)2=KqQ/L2 + KqQ/L2 — F1=√2.K.q.Q/L2 — L – lado do quadrado — FQQ=K.Q.Q/(√2L)2 — FQQ=K.Q.Q/2L2 — resultante nula — F1=FQQ —
√2.K.q.Q/L2 = K.Q.Q/2L2 — √2q=Q/2 — Q/q=2√2 — R- D
31- Figura A:
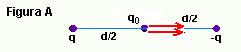
FA=2Kqqo/(d/2)2 — FA=8Kqqo/d2
Figura B:
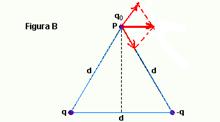
FB=2Kqqo/(d/2)2.cos60o = 2Kqqo/(d/2)2.(1/2) — FB=Kqqo/d2 — FA/FB=8Kqqo/d2 X d2/Kqqo — FA/FB=8
32- Depois do contato cada corpo terá carga de (1 + 5)/2= 3 C
F = k.q.Q/d2 = 9.109.3.3/32 = 9.109 N
A força será repulsiva, pois os dois corpos apresentam a mesma natureza elétrica (são cargas positivas).
R- D
33- Na direção horizontal para qualquer uma das esferas é verdadeiro afirmar que — k.Q2/d2= T.senq — na direção vertical
m.g = T.cosq — dividindo as duas expressões — k.Q2/(m.g.d2) = senq/cosq = 1 (pois q = 45°) — d=Q√k/(mg) —
d=30.10-6.√9.108 — d=90.10-2 — d=90cm — R- B
34- a) FN=20FE=20Kq2/d2=20.9.109.(1,6.10-19)2/1,6.10-15)2 — FN=180.109.10-8 — FN=1.800N — FN=1,8.103N
b)F = q.E = 1,6.10-19.2.106 = 3,2.10-13 N
35- Das informações iniciais sabemos que — F = k.q.q/d2 — F = k.(q/d)2 — na configuração apresentada a força resultante sobre q1 é — Fr = Ö[F212 + F312] — Fr = Ö[(k.3q.q/d2)2 + (k.4q.q/d2)]2 — Fr = Ö[9k2.q4/d4 + 16.k2.q4/d4] — Fr = Ö[25k2.q4/d4] = 5.k.(q/d)2 — Fr = 5.F — R- D
36- Em cada uma das extremidades das quatro diagonais que passam pelo centro do cubo há duas cargas de mesmo módulo e de
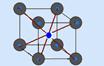
mesmo sinal. Elas exercem na carga central (também de mesmo sinal e mesmo módulo que as dos vértices) forças de mesma intensidade e de sentidos opostos. Portanto, essas forças se equilibram, sendo então nula a resultante dessas forças.
R- A
37-
Na situação inicial, as cargas negativas (-q), nas extremidades, repelem-se com forças de intensidade F, sendo 2 d a distância entre elas — como as cargas negativas estão em equilíbrio, elas trocam forças, também, de intensidade F com a carga positiva (+Q) central, sendo d a distância do centro às extremidades — a lei de Coulomb nos afirma que a intensidade das forças eletrostáticas entre duas cargas varia com o inverso do quadrado da distância entre essas cargas — F=kQq/d2 — na situação final, a distância entre as cargas negativas foi reduzida à metade (de 2 d para d) logo, as forças de repulsão entre elas passam a ter intensidade 4 F — porém, a distância de cada carga negativa à carga central também é reduzida à metade (de d para d/2) quadruplicando, também, as forças de atração entre elas, ou seja, 4 F — portanto o equilíbrio é mantido com Q’ = 1 Q — R- A
38-
Na primeira situação, as forças são atrativas e têm intensidade — F=kQq/d2 (I) — na segunda situação, as forças são repulsivas e têm intensidade — F’=k.4Q.3q/(2d)2 — F’=3kQq/d2 (II) — comparando I com II você conclui que F’=3F e que as forças que eram atrativas passam a ser repulsivas — R- D
39- Como não foi especificada a massa da barra é considerada desprezível, como também a massa da carga suspensa — as forças eletrostáticas entre as cargas têm a mesma direção da reta que passa pelos seus centros — para que o sistema fique em equilíbrio as forças eletrostáticas devem ser de atração — as intensidades da força de tração no fio e das forças eletrostáticas são iguais (T = F), como ilustrado na figura — da figura — cos30o=d/r — r=d/cos30o — r=d/(√3/2) (I) — lei de Coulomb — F=koQq/r2
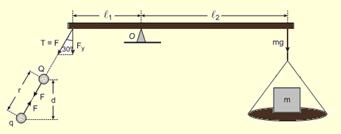
(II) — (I) em (II) — F = koQq/(2d/√3)2 — F=3koQq/4d2 (III) — para que a barra esteja em equilíbrio a somatória dos momentos deve ser nula — adotando o pólo no ponto O mostrado na figura — Fcos30oℓ1=mgℓ2 (IV) — (III) em (IV) — 3koQq√3 ℓ1/4d2.2=mg ℓ2 — 3koQq√3 ℓ1/8d2=mg ℓ2 — q=8mgℓ2d2/3√3koQℓ1
— como as forças entre Q e q são de atração e, se Q é positiva, q só pode ser negativa ou vice versa — R- E
40- Observe as figuras abaixo — no triângulo hachurado da figura 1 — Pitágoras — L2=d2 + z2 —
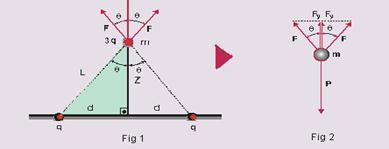
L=√(d2 + z2) (I) — cosθ=z/L — as forças de repulsão mostradas têm intensidade dada pela lei de Coulomb — F=kq3q/L2 — F=k3q2/L2 (II) — (I) em (II) — F=k3q2/(√d2 + y2)2 — F= k3q2/(d2 + y2) (III) — observe na figura 2 que, como a massa m está em equilíbrio a força resultante sobre ela é nula — P=2Fy — mg=2Fcosθ — cosθ=z/L — m=2F(z/L)/g (IV) — (III) em (IV) — m=(2/g).(k3q2/L2).(z/L) — m=6kq2z/gL3 — m=6kq2z/g(d2 + z2)2/3 — R- B
41- Observe as figuras abaixo que mostram as duas situações descritas no enunciado —
F=kQq/d2 (I) — F’=kQq/(2d)2=KQq/4d2 — (I)/(II) — F/F’=kQq/d2 x 4d2/kQq — F/F’=4 — F’=F/4 — R- D
42- a) Observe na figura abaixo a imagem da carga –Q (-Q’) e a decomposição de suas velocidades e das velocidades do espelho nas direções paralelas e perpendiculares ao espelho:
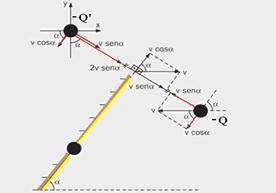
Observe na figura acima que v.senα é a velocidade com que a imagem da carga –Q se aproxima perpendicularmente do espelho e que v.cosα é a velocidade com que a imagem da carga –Q se move paralelamente ao espelho — mas, também, como o espelho se aproxima da carga –Q com velocidade v.senα, a imagem de –Q se aproximará do espelho com velocidade 2v.senα — como o espelho se aproxima de –Q paralelamente ao eixo x, a imagem de –Q não sofrerá deslocamento na direção paralela ao espelho —
Se você somar vetorialmente os vetores velocidades da imagem –Q’ e os decompondo em x e y, obterá — vx=(3vsenα).senα –
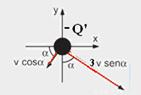
(vcosα).cosα — vx=v(3sen2α – cos2α) — vy= – (3vsenα).cosα – (vcosα).senα — vy= – 4vsenα.cosα — mas sen2α=(1 – cos2α)/2 e sen2α=2senα.cosα — vx=v(3sen2α – (1 – sen2α)) — vx=v(1 – 2cos2α) — vy= – 4vsen2α/2 — vy= – 2vsen2α
b) Aceleração centrípeta da carga negativa — intensidade — ac=v2/r — direção e sentido — vertical e para cima — a figura mostra as forças que agem sobre a carga negativa — a aceleração tangencial tem a direção do eixo x — FR=Fex —
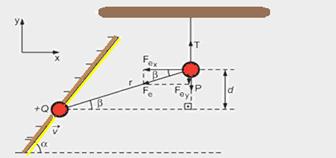
ma=Fecosβ — Fe==kQQ/r2 — ma=kQQ/r2 — r=d/senβ — ma=kQQ/(d/senβ)2.cosβ — a=kQ2sen2βcosβ/md2 — aceleração tangencial — intensidade – at= kQ2sen2βcosβ/md2 — direção – eixo x — sentido – contrário a x.
43- a) Do texto — “Segundo todos os cálculos, as futuras usinas de fusão nuclear poderão extrair de 1 metro cúbico de água uma quantidade de energia igual à de 2 mil barris de petróleo” — regra de três — 1 m3 – 2.103 barris — 100 m3 – n barris —
n=2.103.102 — n=2.105 barris de petróleo — como cada barril contém 1,5.106 kcal, 2.105 barris conterão — W=2.105 barris x
1,5.106kcal/barril — W=3,0.1011 kcal=3,0.1014cal — do enunciado — 1 BEP (Barril Equivalente de Petróleo), equivale a 1,45.109 cal — regra de três — 1 BEP – 1,45.109 cal — n’ BEP – 3.1014 cal — n’=3.1014 cal/1,45.109 cal —
n’≈2,07.105 BEP.
b) Do texto: “Os centros dos núcleos dos átomos de hidrogênio devem estar a 1.10-15 metros um do outro para que ocorra a fusão” — ainda do texto — “essa fusão é o processo no qual dois núcleos de átomos leves (por exemplo, o hidrogênio – cujo núcleo é constituído por 1 próton com carga elétrica elementar é 1,6.10-19C) se combinam, ou se fundem, constituindo um elemento mais pesado. Os núcleos, então, carregados positivamente, devem se aproximar suficientemente um do outro, ou seja, vencer a força de repulsão eletrostática entre eles” — portanto, são dados — d=1.10-15m — .|Q1|= |Q2|=1,6.10-19C — k=9.109N.m2/C2 —
Lei de Coulomb — F=k.|Q1|. |Q2|./d2 = 9.109.1,6.10-19.1,6.10-19/(1.10-15)2 — F=23,04.101 — F=230,4 N.