Resolução comentada das questões de vestibulares sobre o conteúdo Condutor em equilíbrio eletrostático – Blindagem eletrostática
01- R- D — veja teoria
02- R- B
03- A descarga elétrica ocorrida irá eletrizar o avião — porém, como sua fuselagem é metálica (bom condutor), essas cargas irão se distribuir na superfície externa, não causando danos aos passageiros. A fuselagem atua como blindagem para o seu conteúdo.
R- D
04- (01) Falsa — a eletrização ocorre por atrito.
(02) Verdadeira — as cargas elétricas ficam distribuídas pela superfície do condutor, seja ele oco ou maciço (blindagem eletrostática), e consequentemente, o campo elétrico no seu interior é nulo.
(04) Falsa — os isolantes também podem ser eletrizados por atrito.
(08) Verdadeira — o campo elétrico criado nas partes pontiagudas de um condutor eletrizado, pode assumir valores extremamente altos e provocar um fenômeno eletrostático denominado poder das pontas, que consiste na troca de cargas elétricas entre as pontas do corpo eletrizado e o meio isolante que o envolve.
(16) Falsa — o potencial elétrico é o mesmo em todos os pontos da superfície de um condutor em equilíbrio eletrostático, portanto a superfície é eqüipotencial.
(32) Verdadeira Internamente o potencial elétrico é constante e igual ao potencial na superfície.
R- (02 + 08 + 32)=42
05- R- (02+04+16)=22
06- I. Verdadeira — todos os pontos internos e da superfície possuem o mesmo potencial.
II. Falsa — é mais intenso em B (ponta)
III. Verdadeira
R- D
07- R- C — veja teoria
08- O campo elétrico é mais intenso onde existir maior densidade de carga o que acontece nas pontas (nos vértices), onde o raio de curvatura é menor.
R- C
09- R- D
10- R- D — veja teoria
11- Se uma penitenciária fosse envolvida por uma malha metálica, onde os “buracos” tivessem dimensões menores de 15 cm, não haveria a penetração de campos elétricos em seu interior, tornando-a blindada a ondas eletromagnéticas na faixa da telefonia móvel (da ordem de 1.800MHz). No entanto, isso não é feito pelo alto custo, preferindo-se a utilização da interferência, emitindo-se ondas nessa faixa de freqüência com intensidade muito maior.
R- E
12- a) Falsa — a carga induzida na esfera maior estará distribuída pela sua superfície externa, havendo maior concentração próxima da esfera menor.
b) Verdadeira — veja teoria
c) Falsa — no interior da esfera maior, o campo elétrico será não-nulo devido à carga –Q da esfera menor e, na parte externa, o campo elétrico será também não-nulo, devido à carga –Q e à carga +Q (induzida na superfície externa da esfera maior).
d) Falsa — se o fio condutor, a carga –Q irá para a superfície externa da esfera maior, proporcionando um campo elétrico nulo na parte interna dessa esfera.
R- B
13- Nas pontas de um condutor eletrizado, encontramos uma quantidade maior de cargas por unidade de área.
R- A
14- O campo elétrico é nulo nos pontos internos de um condutor eletrizado e em equilíbrio, independentemente da sua forma.
R- E
15- 01. Correta — com S1 ligada, cargas elétricas negativas do gerador fluirão até a esfera condutora maciça eletrizando-a, que por sua vez induzirão cargas positivas na superfície externa da casca esférica condutora que também induzirão cargas no pêndulo, que continua neutro, atraindo-o por indução elétrica.
02. Correta — veja em fisicaevestibular o processo de eletrização por indução.
04- Falsa — a casca esférica eletrizada origina campo elétrico ao seu redor.
08. Correta — veja 02
16- Falsa — veja 01
R- (01 + 02 + 08)=11
16- d=Q/S — d=Q/4πR2 — 10-6=Q/4π(5.10-1)2 — Q=102.π.1-2.10-6 — Q=π.10-6C — R- A
17- Sendo o raio da esfera de 0,5m=50cm, o ponto distante 30cm do centro da esfera está em seu interior — E=0 — R- D
18- a) E=KQ/d2+ — 9.104=9.109.Q/4 — Q=4,0.10-5C — b) não é nulo, é constante e diferente de zero — c) V=KQ/R=9.109.
4.10-5/1 — V=36.104V — d) V=9.109.4.10-5/4 — V=9.104V — e) E=9.109.4.10-5/9 — E=4,0.104N/C
R- E
19- R- D
20- VA=KQA/RA — 9=9.109QA/10.10-2 — QA=10-10C — Q’A/Q’B=RA/RB=10.10-2/5.10-2 — Q’A=2Q’B — QA + QB= Q’A + Q’B — 10-10 + 0 = 2Q’B + Q’B — Q’B=10-10/3 — Q’B=0,33.10-10C — Q’A=0,66.10-10C — R- A
21- a) Essa rigidez equivale ao campo elétrico próximo da esfera — Epróximo=3.106N/C — Epróximo=KQ/R2 — Epróximo=Esuperfície/2 — Esuperfície=2 Epróximo — Esuperfíe=2.3.106=6.106N/C — 6.106=9.109.Q/(3.10-1)2 — 6.106=9.109Q/9.10-2 — Q=6.106/109 — Q=6.106/1011 — Q=6.10-5C ou Q=60μC
b) V=KQ/R=9.109.6.10-5/3.10-1 — V=18.105V ou V=1,8MV
22- Q1=4.10-3C — Q’1/Q’2=R1/R2 — Q’1/Q’2=5.10-2/15.10-2 — Q’1/Q’2=3 — Q’2=3Q’1 — Q1 + Q2= Q’1 + Q’2 — 4.10-3 + 0 = Q’1 + 3Q’1 — 4 Q’1=4.10-3 — Q’1=10-3C — Q’2=3.10-3C — R- D
23-
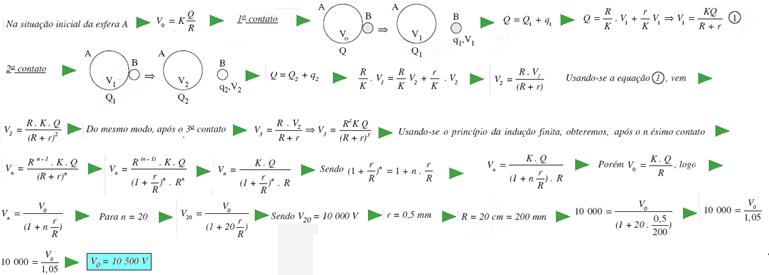
24- Na pequeníssima esfera (ordem de micrômetros) — R=10-6m — S = 4pR2 = 4.3.(10-6)2=12.10-12 m2 isto significa que é da ordem de 10-11 m2 — Q = 10.000.1,6.10-19 = 1,6.10-15 C — isto significa da ordem de 10-15 C
A densidade superficial de carga será — d=Q/S = 10-15C/(10-11 m2) — d=10-4 C/m2 — na pequena esfera (ordem de milímetros) — R=10-3m — S = 4pR2 = 4.3.(10-3)2=12.10-6 m2 — que significa da ordem de 10-5 m2 — usando a densidade de carga anterior tem-se — Q=d.S=10-4S=10-4..10-5 — Q=10-9C — o número de cargas elementares deverá ser da ordem de —
n = Q/e = 10-9/(1,6.10-19) = 0,625.1010 = 6,25.109 que tem ordem de grandeza em 1010, visto que a parte significativa é maior que a √10=3,16 — R- D
25- Em um condutor eletrizado o campo elétrico em seu interior é nulo — o potencial elétrico no interior é igual ao potencial elétrico na superfície.
R- B
26- Todo excesso de carga tenderá a repelir e ficarão concentrados na superfície da esfera externa — R- E
27- Q1/Q2=R1/R2=2R2/R2 — Q1=2Q2 — σ1=Q1/S1=2Q2/4πR12=2Q2/4π(2R2)2 — σ1=Q2/8πR22 — σ2=Q2/4πR22 — σ1/σ2=Q2/8πR22 X 4πR22/Q2 — σ2=2 σ1 — R- C
28- 00. Falsa — o potencial elétrico é o mesmo, constante e diferente de zero, pois estão ligados por um fio condutor.
01. Falsa — é o mesmo no interior e na superfície.
02. Verdadeira — QA/QB=RA/RB=6/2 — QA=3QB
04. Verdadeira — QA+ QB=8.10-8 — 3QB + QB=8.10-8 — QB=2.10-8C — QA=6.10-8C — V=KQ/R=9.109.2.10-8/2.
10-2=9.109.6.10-8/6.10-2 — V=9.103V
29- 01- Falsa — no contato a carga total do sistema será +q e os potenciais das esferas condutoras na superfície deverão ser os mesmos — m + n = q — onde m e n são as cargas das duas esferas após a separação das mesmas — Ko.m/R = ko.n/(2R) —
m = n/(2) — n = 2.m — m + n = q — m + 2.m = q — 3.m = q — m = q/3 e n = 2q/3 — desta forma a força entre as esferas — F = ko.m.n/a2 = ko.(4q2/9)/a2 o que invalida a afirmação (01).
02. Correta — as cargas são diretamente proporcionais aos raios das esferas.
04. Falsa — após o contato o potencial elétrico é o mesmo.
08. Correta — veja teoria
16. Correta — veja teoria
32. Falsa — no interior da esfera o potencial é constante e diferente de zero e, assim a diferença de potencial é nula.
R- (02 + 08 + 16) = 26
30- Dados: q = 4.10-6 C — d = 0,2 m = 2.10-1 m — k = 9.109 N.m2/C2.
a) O campo eletrostático gerado pela partícula no centro da esfera maciça é dado pela lei de Coulomb:
E = kq/r2 — E = 9.109.4.10-6/(2.10-1)2 — E = 9,0.105 N/C, no sentido indicado na Fig 1.
b) Analisando a Fig 2 — como a esfera condutora está em equilíbrio eletrostático, o vetor campo elétrico resultante no seu interior é nulo. A partícula eletrizada induz cargas elétricas negativas (–) e positivas (+) na superfície da esfera, gerando um outro
campo elétrico no seu interior (
31- O atrito da pele das pessoas com objetos isolantes (lã, flanela, papel, plástico) tornam a pele eletrizada — em dias normais, esse excesso de cargas é descarregado no contato com o próprio ar — porém, em dias secos, esse processo torna-se muito lento, acumulando cargas estáticas — no contato com objetos, principalmente metálicos, ocorre uma brusca descarga, que é o choque elétrico — R- B
32- I. Falsa — só o campo elétrico é nulo, o potencial elétrico é constante e diferente de zero.
II. Falsa — EB=Epróximo/2=V/2R — veja teoria
III. Falsa — V=KQ/2R
IV. Correta — EC=KQ/(2R)2=KQ/4R2 (1) — VC=KQ/2R (2) — comparando (1) com (2) — EC=VC/2R
R- B
33- E=KQ/d2=9.109.2.10-6/9.10-4 — E=2,0.107N/C — F=KQq/d2=9.109.2.10-6.5.10-9/9.10-4 — F=1,0.10-1N — V=KQ/d=9.109.2.
10-6/3.10-2 — V=6,0.105 V — R- C
34- a) Falsa — W=qo.(VA – VB) — como o potencial é constante em pontos interiores da esfera — VA=VB — W=qo.0 = 0
b) Falsa — o trabalho realizado nessas condições é calculado como se toda carga Q estivesse no centro da esfera — W=qo.VA – VB), com V=KQ/d
c) Falsa — a medida que ela vai sendo carregada o potencial vai aumentando
d) Correta — d=Q/S=Q/4πR2 — Q e R são fornecidos pelo gráfico.
e) Falsa — o campo elétrico é nulo no interior da esfera.
R- D
35- No interior de um condutor (caixa metálica) em equilíbrio eletrostático, as cargas distribuem-se na superfície externa do condutor, anulando o campo elétrico no seu interior. Esse fenômeno é conhecido como blindagem eletrostática.
R- B
36- Capacitância C — C = εo A/d = 9.10-12.5.10-4/2.10-3 — C = 2,25.10-12 F — diferença de potencial V entre o rolo e a fita —
V=Q/C=4,5.10-9/2,25.10-12 — V=2.0.103 V — R- C
37- I. Falsa — essa força é fornecida por F=KQq/d2 e K é uma constante que depende do meio onde as cargas estão imersas.
II. Correta — depois do contato o bastão neutro ficou com carga positiva, ou seja, perdeu elétrons.
III. Falsa — só se eletrizam se forem de materiais diferentes e na eletrização por atrito terão sempre cargas de mesmo módulo mas sinais contrários.
IV. Correta — Define-se superfície equipotencial de um campo elétrico a qualquer superfície em cujos pontos o potencial elétrico é constante.
Estas superfícies têm duas propriedades importantes:
1a – A força elétrica durante o deslocamento de uma carga elétrica puntiforme sobre uma superfície equipotencial é nula.
2a – As superfícies equipotenciais são perpendiculares às linhas de força ou linhas de campo elétrico e, conseqüentemente, perpendiculares ao vetor campo elétrico e à qualquer ponto da superfície. .
V. Falsa — o campo elétrico em seu interior é nulo — é o potencial elétrico que é constante.
R- A.
38- Campo e potencial elétrico de um condutor esférico:
Leia atentamente as informações abaixo:
01. Correta.
02. Falsa — é inversamente proporcional a D2.
04. Correta — A densidade elétrica superficial (σ) mede a concentração de carga elétrica (Q) pela superfície (área S) — σ=Q/S — no caso de esfera de raio R, a área da superfície esférica é fornecida por S=4πR2.
08- Falsa — veja gráfico acima — ele é constante e vale V=KQ/R.
16. Correta — todos os pontos internos e da superfície possuem o mesmo potencial de valor V=KQ/R.
Corretas: 01, 04 e 16 — Soma=21.
39- 01. Correta — observe o campo elétrico uniforme da figura abaixo onde as linhas de força e
consequentemente o campo elétrico se afasta a placa eletrizada com cargas positivas onde o potencial elétrico é maior — uma carga positiva aí colocada se afãs da placa positiva (é repelida) e se aproxima da placa negativa (é atraída) — se deslocando de A para B ou seja, para pontos de menor potencial elétrico.
02. Falsa — observe na figura abaixo que a carga negativa se desloca para a esquerda, atraída pela placa positiva e
repelida pela negativa, ou seja, se desloca em sentido contrário ao do campo elétrico.
04. Correta — Define-se superfície equipotencial de um campo elétrico a qualquer superfície em cujos pontos o potencial elétrico é constante.
Estas superfícies têm duas propriedades importantes:
1a – A força elétrica durante o deslocamento de uma carga elétrica puntiforme sobre uma superfície equipotencial é nula.
2a – As superfícies equipotenciais são perpendiculares às linhas de força ou linhas de campo elétrico e, conseqüentemente, perpendiculares ao vetor campo elétrico
No caso particular do campo de uma carga puntiforme, a simetria sugere que são superfícies esféricas concêntricas com a carga e as linhas de força (de campo) são radiais com o centro da carga.
Campo Elétrico Uniforme
Um campo elétrico uniforme tem em todos os seus infinitos pontos mesma intensidade, mesma direção e mesmo
sentido e é obtido entre duas placas condutoras idênticas e paralelas e eletrizadas com cargas de mesmo módulo, mas de sinais contrários.
Observe que nesse caso as superfícies equipotenciais são planas e paralelas entre si.
08. Correta — se existe campo elétrico tem que existir potencial elétrico.
16. Correta — o trabalho de qualquer força conservativa não depende da trajetória, mas apenas das posições inicial e final da mesma.
Corretas: 01, 04, 08 e16 — Soma=29.
40- Blindagem eletrostática – Se, no interior de um condutor oco em equilíbrio eletrostático o campo elétrico
elétricas. Construções também são feitas utilizando blindagem eletrostática, a fim de proteger seus equipamentos elétricos e eletrônicos.
R- B
41-
a) Cargas negativas (íons negativos – Cl–) deslocam-se para pontos de maior potencial, do interior para o exterior da célula — cargas positivas (íons positivos – Ca2+) deslocam-se para pontos de menor potencial, do exterior para o interior da célula.
b) No interior da membrana (interior do capacitor), pelo gráfico a ddp U=(64.10-3 – 0)=64.10-3m — U=E.d — 64.10-3=E.8.10-9 — E=8,0.106V/m ou N/C.
c) Força elétrica sobre os íons Cl– — FCl=|q|.E=1.1,6.10-19.8.106 — FCl=1,28.10-12N — força elétrica sobre os íons Ca2+ — FCa=|q|.E=2.1,6.10-19.8.106 — FCl=2,56.10-12N.
d) Pela definição de capacitância, sendo Q a carga elétrica na superfície externa da membrana — C=Q/U — 12.10-12=Q/64.10-3 — Q=7,68.10-13C.