Força Eletromotriz Induzida – Transformadores – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Força Eletromotriz Induzida – Transformadores
01– A corrente está sendo induzida (indução eletromagnética) e muda de sentido no “vai e vem” do imã — R- A
02- Fluxo inicial — Φo =37.10-3Wb — fluxo final — Φ=0 — variação de fluxo — ΔΦ=Φ – Φo=37.10-3 – 0 — ΔΦ=37.10-3Wb — ε=ΔΦ/Δt=37.10-3/10-3 — ε=37V
03- 01. Correta — quando a espira gira, o fluxo magnético através dela sofre variação e surge uma força eletromotriz induzida que gera uma corrente elétrica induzida.
02. Correta — Lei de Lenz
O4. Correta — veja teoria
08. Falsa — com a espira parada não ocorre variação de fluxo magnético.
16. Correta — Φ=B.S.cosα — valor máximo — Φ=B.S.cos0o=2.10-2.1.10-3.(+1)=+2,0.10-5T.m2 — valor mínimo — Φ=B.S.cosα=2.10-2.1.10-3.cos180o=2.10-5.(-1)=-2,0.10-5T.m2 — R- (01 + 02 04 + 16) = 23
04- L=10cm=0,1m — S=L.L=0,1.0,1=0,01m2 — Φi=0 — Φf=B.S=1.0,01=0,01T — ΔΦ= Φf – Φi=0,01 – 0=0,01T —
ε=ΔΦ/Δt=0,01/2 — ε=0,005V — R=U/i — R=ε/i — 0,2=0,005/i — i=0,025ª — i=25mA
05- ε=BLV — 3.10-3=B.2.60 — B=2,5.10-5T
06- No intervalo d, onde 
varia, e consequentemente o fluxo magnético também varia — R– E
07- ε=ΔΦ/Δt=2/1 — ε=2V — R=U/i — R=ε/i — 4=2/i — i=0,5A
08- I – Como a área das espiras está aumentando (fluxos induzido e indutor tem sentidos contrários) e o fluxo induzido pela corrente está saindo da página (regra da mão direita), o fluxo indutor está entrando na página — Correta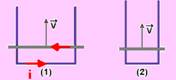
II – Correta — mesmo campo magnético que o da 1, áreas aumentando e consequentemente mesmo sentido de corrente.
III – Falsa — as expressões (Φ=B.S.cosα e ε=ΔΦ/Δt) mostra que a fem induzida depende da área S.
R- A
09- a) Ptotal=F/A=P/A=mg/A — Ptotal=2,16.105.10/(0,5).(0,5) — Ptotal=86,4.105N/m2 — um suporte — P=86,4.105/12 — P=7,2.105N/m2
b) Variação de fluxo de 1 espira Φf=B.S=1,5.10-2.π.R2=1,5.10-2.3.4 — Φf=18.10-2Wb — Φi=0 — ΔΦ=18.10-2Wb — força eletromotriz de uma espira — ε= ΔΦ/Δt=18.10-2/5.10-2=3,6V — uma espira – ε=3,6V — 10.000espiras — ε=3,6.104V
10- R- C
11- S=0,2.0,3 — S=0,06m2 — intervalo I — ΔΦ=(6.0,06 – 0.0,06)=0,36Wb — ε= ΔΦ/Δt=0,36/0,3 — ε=1,2V — R=ε/i — 3=1,2/i — iI=0,4 A — intervalo II — ΔΦ=(6.0,06 – 6.0,06)=0,0 — ε= ΔΦ/Δt=0,0/0,3 — ε=0 — iII=0 — intervalo III — ΔΦ=(0.0,06 – 0,6.0,06)= – 0,36Wb — ε= ׀ΔΦ׀/Δt=0,36/0,6 — ε=0,6V — R=ε/i — 3=0,6/i — iIII=0,2 A — R- B
12- S=0,10.0,10=0,01m2 — variação de fluxo entre 0 e 16.10-3s — ΔΦ=8.10-3 – 0=8.10-3Wb — ε= ΔΦΔt=8.10-316.10-3 — ε=0,5V — R=εi — 20=0,5/i — i=0,025 A — R- D
13- ε=B.L.V=4.0,02.0,2 — ε=0,016V — ε=1,6.10-2V — como o fluxo através da espira está aumentando, o fluxo induzido deve se opor a esse aumento e o campo magnético induzido deve estar saindo do papel — usando a regra da mão direita com saindo do papel, a corrente elétrica induzida será no sentido anti-horário.
14- Fluxo total através da bobina — Φtotal=nB.S=20.0,2.25.10-6 — Φtotal=100.10-6=10-4Wb — a velocidade escalar de um ponto da periferia da roda de raio R=60/2=30=0,3m, é V=36km/h=10m/s
— velocidade angular da roda da roda — W=V/R=10/0,3 — W=100/3rad/s — esta velocidade angular é a mesma onde estão os imãs de raio R=0,15m — W=V/R — 100/3=V/0,15m — V=5m/s (velocidade escalar dos imãs) — ΔS=um dos lados da espira quadrada de área 25mm2 — L=5mm=5.10-3 — V= ΔS/Δt — 5=5.10-3/Δt — Δt=10-3s (tempo que a bobina demora para variar o fluxo de 0 até o valor máximo) — fem máxima — ε=ΔΦ/Δt=10-4/10-3 — ε=10-1V — R- D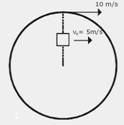
15- R- A – Veja teoria
16- S=πR2=3.(2.10-2)2 — S=12.10-4m2 — entre 0 e 5.10-2s — ΔΦ=B.S – Bo.So=5.10-4.12.10-4 – 0=6.10-7Wb — ε= ΔΦ/Δt= 6.10-7/5.10-2 — ε=1,2.10-5V — ε=12μV
17- De acordo com a Lei de Faraday-Lenz, o deslocamento da barra metálica, levando à variação do fluxo magnético através da área delimitada pela barra metálica e pelos trilhos, gera uma força eletromotriz no circuito. Por outro lado, na medida em que a barra metálica é percorrida por uma corrente elétrica e está situada em uma região em que há campo magnético, sobre ela atuará uma força magnética. A força eletromotriz gerada se contrapõe ao efeito que a gera e desse modo a força magnética que atua sobre a barra metálica é contrária à tensão no fio ao qual está conectada a massa M.
A força eletromotriz gerada é dada por ε= Blv, em que v é a velocidade da barra metálica e a força magnética sobre a barra é
Fm = P — Bil=mg — 0,2=i.1=0,04.10 — i=2A — R=U/i=ε/i — 0,5=ε/2 — ε=1V — ε=BLV — 1=0,2.1.V — V=5m/s
18- A corrente i na barra tem sentido de M para N e aplicando a regra da mão esquerda você descobre que a força magnética sobre a barra é para a esquerda e ela se move nessa direção e sentido com aceleração constante já que a força é constante — R- E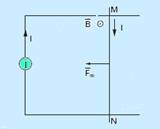
19- Quando a velocidade da barra se tornar constante ela estará em equilíbrio dinâmico e a resultante sobre ela será nula — decompondo a força peso da barra na direção do movimento — Pp=Psen30o=mgsen30o==5.10.0,5 — Pp=25N — essa força é equilibrada pela força magnética perpendicular ao plano da espira de intensidade — Fm=BiLsen90o=Bi1.1 — Fm=Bi —
Fm=Pp — Bi=25 (I) — a fem induzida no circuito vale — ε=BLV — R=ε/i — ε=Ri — Ri=BLV — 2.i=B.1.2 — B=i (II) — II em I — B.B=25 — B2=25 — B=5T — R- E
20- O alumínio é um material Paramagnético, ou seja, fracamente atraído pelo ímã. Como está eqüidistante dos pólos do ímã a força resultante no anel no eixo N – S é nula. Porém, o fluxo de linhas de indução no interior do anel é variável e cria uma pequena corrente induzida e consequentemente uma força eletromotriz induzida. Então, passam a agir sobre o anel forças magnéticas que se opões ao movimento, diminuindo lentamente a oscilação — R- A
21- ΔΦ= Φ2 – Φ1=2,3.10-3 – 0,3.10-3 — ΔΦ=2,0.10-3Wb — ε= ׀ΔΦ׀Δt=2.10-3/0,5 — ε=4.10-3V — R=ε/i — 1=4.10-3/i —
R- i=4mA
22-
Entre 0 e 4s — ε=ΔΦ/Δt=(BfSf – BoSo)/Δt=(2.0,5 – 0.0,5)/4 — ε1=0,25V — Entre 4s e 6s — ε=ΔΦ/Δt=(BfSf – BoSo)/Δt=(2.0,5 – 2.0,5)/4 — ε2=0 — Entre 6s e 8s — ε=ΔΦ/Δt=(BfSf – BoSo)/Δt=(-2.0,5 – 2.0,5)/4 — ε3= -1,0V — Entre 8s e 11s — ε=ΔΦ/Δt=(BfSf – BoSo)/Δt=(0.0,5 – (-2.0,5)/3 — ε4= 0,33V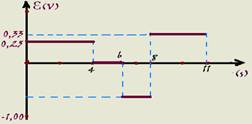
23- Quando t=0 — Φo=0 — quando t=4s — Φ=B.S=4.4.10-2Wb — ε=ΔΦ/Δt=(16.10-2 – 0)/2 — ε=8.10-2V — esta é a fem criada por uma espira — como são 100 espiras — ε=100.8.10-2 — ε=8V
24- Área do aro — S=πR2=3.(0,4)2 — S=0,48m2 — fluxo inicial – Φo=0 — fluxo final – Φ=B.S.cos0o=1,0.0,48.1 — Φ=0,48Wb — ΔΦ=(Φ – Φo)=0,48Wb — fem induzida — ε=ΔΦ/Δt=0,48/0,4 — ε=1,2V
25- R=4/2cm=2.10-2m — S=πR2=3.4.10-4 = 12.10-4m2 — ΔΦ=B.S=103.12.10-4=1,2Wb — ε=ΔΦ/Δt=1,2/1 — ε=1,2Wb/s — ε=1,2V — este valor é de uma espira — para 30.000 espiras — ε=3.104.1,2 — ε=36.000V
26- As asas do avião se comportam como se fossem um condutor retilíneo em movimento, atravessando o campo magnético da Terra e consequentemente induzindo uma força eletromotriz (diferença de potencial) entre os extremos de suas asas — R- E
27- As asas do avião se comportam como se fossem um condutor retilíneo em movimento, atravessando o campo magnético da Terra e consequentemente induzindo uma força eletromotriz entre os extremos de suas asas — ε=BVL=5.10-5.200.60 —
ε=60.000.10-5 — ε=0,6V
28- A corrente elétrica induzida é uma função senoidal do tempo e é alternada porque ela percorre a espira ou bobina invertendo seu sentido durante um ciclo, como indica o gráfico i X t.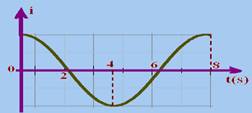
Observe na seqüência do enunciado que, quando t=o o fluxo e consequentemente a corrente são máximos e que o ciclo se completa quando t=8s.
29- a) Potência do LED — P=i.U — 24.10-3=20.10-3.U — U=1,2V
b) ΔΦ=B.ΔS=1,1.0,4.0,6 — ΔΦ=0,264Wb
c) V=׀ε׀= ΔΦ/Δt — 1,2=0,264/Δt — Δt=0,22s
30- a) B=μoi /2π r — 10-5=4.π10-7.i/2π.2,5.10-2 — i=1,25A
b) ε= -ΔΦ/Δt — ΔΦ= ΔB.A=(5.10-6 – 0).0,6.10-4/2.10-3 — ε= -1,5.10-7V — em módulo — ε=1,5.10-7V
31- R- A — veja teoria
32- R- C — veja teoria
33- R- E — veja teoria
34- Um transformador só funciona com corrente alternada — R- C
35- “as tensões (voltagens) U1 e U2 são diretamente proporcionais ao número de espiras N1e N2”
R- E
36- R- E — veja teoria
37- R- B — veja teoria
38- 01. A potência do primário é sempre igual à do secundário (princípio da conservação da energia) — Correta
02. Falsa — a bateria fornece corrente contínua e, sem corrente alternada não haverá fem induzida.
04. Correta — veja 01
08. As correntes são inversamente proporcionais às tensões — Falsa
16. Este fenômeno é devido à indução eletromagnética — Falsa
R- (01 + 04) = 05
39- Como o gerador (bateria) só produz corrente contínua, só haverá deflexão do ponteiro do galvanômetro quando houver variação de corrente o que ocorre quando a chave é ligada (aumento de corrente) ou desligada (diminuição de corrente) — R- B
40- R- Soma (02 + 04) = 06 — veja teoria
41-
42- a) 8.800/220=N1/N2 — N1/N2=40
b) A potência é a mesma no primário e no secundário — cálculo da potência no secundário 2 — Ps2=Us2.is2 — Ps2=220.150 — Ps2=33.000W — a potência total no primário é a soma das potências nos dois secundários — P1=Ps2 + Ps1 — 81.000=33.000 + Ps1 — Ps2=48.000W — Ps1=Us1.is1 — 48.000=120.is1 — is1=400A
43- i1=2 A — U1=80V — i2=40 A — U1/U2=i2/i1 — 80/U2=40/2 — U2=4,0V — U1/U2=N1/N2 — 80/4=N1/N2 — N1/N2=20 — R- D
44- 01) Falsa — a intensidade da força eletromotriz induzida é diretamente proporcional ao módulo da variação do fluxo magnético
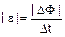
em função do tempo, conforme a lei de Neumann-Faraday:.
02) Correta — a lei de Lenz afirma que sempre que há variação do fluxo magnético, surge uma força magnética na tendência de anular o movimento que deu origem a essa variação do fluxo.
04) Correta — dados: n = 50 espiras — i = 2 A — P = 5 W — P = U i — P = n.i.U — 5 = 50. 2.U — U=0,05 V.
16) Correta — com o circuito aberto, não há condução.
32) Falsa — parte desse trabalho é dissipado na forma de calor na bobina e na lâmpada.
R- (02 + 04 + 16) = 22
45- a) Dados — U1 = 110 V — U2 = 220 V — N1 = 250 espiras — sendo N2 o número de espiras
correspondente a 220 V — equação do transformador — U1/N1=U2/N2 — 110/250=220/N2 — N2=500 espiras
b) P = 880 W — P=U2i2 — 880=220.i2 — i2=4 A — P=U1.i1 — 880=110.i1 — i1=8 A
c) Pmáx=2.200 W — Pmáx=U2.i2máx — 2.200=220.i2máx — i2máx=10 A — Pmáx=U1.i1máx — 2.200=110.i1máx — i1máx=20 A
46- Nas usinas hidrelétricas, só haverá corrente elétrica induzida se houver variação de fluxo
magnético o que só é possível girando a espira e, assim, a corrente elétrica produzida é alternada e, é esse tipo de corrente que o transformador recebe — essa corrente elétrica induzida é uma função senoidal do tempo e é alternada porque ela percorre a espira ou bobina invertendo seu sentido durante um ciclo, como indica o gráfico i X t.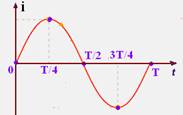
R- B
47- I. Correta — descoberta revolucionária no campo da Física, ocorrida em 1831.
II. Correta — sempre que há variação do fluxo magnético, surge força eletromagnética no sentido de anular a variação desse fluxo — surge também a força eletromotriz induzida (f.e.m)
III. Correta — a força eletromotriz induzida provoca a aparição de uma corrente elétrica induzida.
R- E
48- B=0,5Wb/m2=T — ф=B.S.cosα — фinicial=B.S.cos0o =0,5.(0,1×0,1).1 — фinicial=0,005Wb — фfinal=B.S.cos180o= =0,5.(0,1×0,1).(-1) — фfinall= – 0,005W — ∆ф=- 0,005 – ,005= – 0,01Wb — em módulo — ε=∆ф/∆t — 5=0,01/∆t —
∆t=0,01/5=1×10-2/5=0,2.10-2 — ∆t=2,0.10-3s — R- C
49- Num transformador ideal, a relação entre tensões (V) e correntes (i) é dada pela conservação da energia — a potência no primário é igual à potência no secundário — P1= P2 — V1. i1 = V2. i2 — se V1 > V2 — i1 < i2 — relação entre as tensões (V) e os números de espiras (N) — V1/N1=V2/N2 — se V1 > V2 — N1 > N2 — R- C
50- Existem três maneiras de aumentar a intensidade do campo magnético em uma bobina, também conhecida por solenóide — aumentando o número de espiras — aumentando a intensidade de corrente elétrica e — inserindo um material ferromagnético no interior das espiras — a intensidade da corrente induzida depende da variação do fluxo magnético gerado pela corrente na bobina — quanto mais intensa for a corrente na bobina, maior será a intensidade da corrente induzida no cérebro.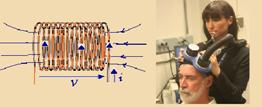 
R- C
51- T=5.10-2 s — velocidade angular w — w=2πf=2.π.20 — w=40π rad/s — substituindo esses
valores na função dada — ф = B.S.coswt = 2.10-5.10-3.cos 40πt — ф = 2.10-8.cos 40πt — quando t = 0, o fluxo é máximo e vale — фmáximo=2.10-8.cos0o — фmáximo=2.10-8Wb — quando t=T/2, a espira efetuou meia volta e o fluxo através dela é mínimo e de valor — фmínimo= 2.10-2.cos 40π.5.10-2/2 = 2.10-2.cosπ=2.10-8.(-1) — фmínimo = – 2.10-8 Wb — observe ao lado o gráfico pedido: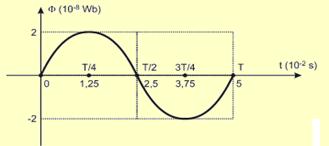
52- Dados — N = 10 espiras — D = 10 cm = 10-1 m — B = 10-2 T — f = 2 Hz — expressão do fluxo magnético — ф=N.B.S.cosα — N – número de espiras — S – área de fluxo através da espira — B – intensidade do vetor indução magnética — α – ângulo formado entre as linhas de indução magnética (
) e a normal (
) ao plano da espira — observe que, para a situação inicial, e
são paralelos, ou seja, α=0o — фinicialL= N.B.S.cosα=N.B.πR2.cos0o — фinicial=10.(10-2).π.(D2/4).1=10-1.(π.10-2)/4 —
Фinicial=2,5.π.10-4 Wb — observe que, para a situação final, depois de um giro de 90o, e são perpendiculares, ou seja, α=90o — фfinal=N.B.S.cos90o — фfinal=0 — o tempo decorrido entre as situações final e inicial é de 1/4de rotação ou de 1/4 do período T — ∆t=T/4 — T=1/f=1/2 — ∆t=(1/2)/4 — ∆t=1/8 s — lei de Faraday-Neumann — ε= – ∆ф/∆ — ε = – (0 -2,5π.10-4)/(1/8) — ε≈ 6,3.10-3 V
53- 01. Falsa — depende também da intensidade da corrente elétrica que percorre a espira e dos raios das espiras.
02. Falsa — quando a corrente i circula pelos fios da bobina, produz nela um campo magnético variável invertendo periodicamente sua polaridade — mas, estando a bobina imersa no campo magnético uniforme de um imã, ela passa a vibrar, fazendo vibrar também o cone — observe que não ocorre indução eletromagnética.
04. Falsa — a vibração do cone produz no ar ondas longitudinais onde a direção de propagação coincide com a direção de vibração das partículas do ar.
08. Correta — a altura do som está relacionada com a frequência (som agudo, frequência mais alta, som grave, frequência mais baixa).
16- Correta — quanto maior a intensidade da corrente elétrica na bobina, mais intenso será o campo magnético por ela gerado e, consequentemente, maiores serão as forças de atração e de repulsão trocadas entre o imã e a bobina — isso aumenta a amplitude do movimento vibratório, aumentando também sua intensidade.
32- Correta — veja justificativa anterior
R- (08 + 16 + 32)= 56
54-
Observe atentamente as expressões abaixo:
01- Falsa — a força eletromotriz induzida ε é nula, pois B é constante e o fluxo magnético Φ não sofre variação.
02. Falsa — área da espira — S=π.r2=π.(0,4/√π)2 — S=0,16m2 — t=0 — Φ=0 — t=1s — Φ=1.0,16=0,16T —
∆Φ=0,16 – 0=0,16Wb — ε=-∆Φ/∆t=0,16/1= – 0,16V.
04. Falsa — ε vale + 0,16V (veja 02)
08. Correta — entre t=5s e t=6s, ε=0,16V (veja 04) — R= ε/i — 8=0,16/i — i=0,02 A.
16. Correta — Φ=B.S e, como S é constante a variação de B é proporcional à variação de Φ.
32. Falsa — a força eletromotriz é calculada com base na lei de Lenz.
Corretas: 08 e 16 — Soma=24.
55- A intensidade da força magnética (
) sobre o fio vale — Fm=B.i.L.sen90o =B.i.L.1=B.i.L=B.i — a parcela da f força peso responsável pela descida do fio no plano inclinado de 30o vale — Pp=m.g.sen30o=5.10.1/2=25N — quando o fio se move com velocidade constante ele está em equilíbrio dinâmico e a força resultante sobre ele é nula (
) e, para que isso ocorra Fm=Pp — B.i=25 — i=25/B (I) — a força eletromotriz induzida ε é fornecida por ε=B.L.v — R=U/i=ε/i — ε=R.i — ε=2.i — 2.i=B.L.v — 2i=B.1.2 — i=B — substituindo em (I) — B=25/B — B2=25 — B=5 T — R- C.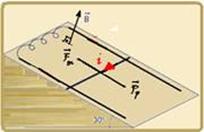
56- A tensão Vrs entre r e s da barra corresponde à força eletromotriz induzida fornecida pela lei de Lenz — ε=Vrs=|∆Φ|/∆t — por essa expressão, quanto maior for a velocidade da barra rs, maior será a variação da área da espira, maior será a variação do fluxo magnético ∆Φ e consequentemente maior será a tensão Vrs induzida — a velocidade de rs e a tensão Vrs são maiores em (3) onde a velocidade é máxima e nulas em (1) e (4) onde a velocidade é nula — R- C.
57-(AFA)
A lei de Faraday-Neuman afirma que a força eletromotriz ε (tensão, ddp) induzida, num mesmo intervalo de tempo ∆t, é tanto maior quanto maior for a variação (∆Φ) do fluxo magnético de 
— ε=∆Φ/∆t — a lei de Ohm fornece a intensidade de corrente elétrica que surge na espira de resistência R com a variação do fluxo do vetor campo magnético campo magnético — R=U/i= ε/i — ε=R.i — =∆Q/∆t — ∆Q=n.e — n – número de elétrons — e – módulo da carga de um elétron — i=n.e/∆t — ε=R.i=R. n.e/∆t — ∆Φ/∆t = R. n.e/∆t — n= ∆Φ/R.e — observe que o número de elétrons n independe de qualquer intervalo de tempo de oscilação do imã, inclusive se seu período T — R- D