Força magnética sobre um condutor retilíneo – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Força magnética sobre um condutor retilíneo

01-

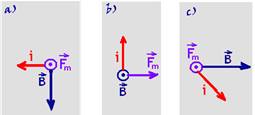
02- Caso(a)  —  F(a)=B.i.L.sen45⁰=(√2/2).BiL  —  caso (b)  —  F(b)=BiL.sen90⁰=BiL  —  caso (c)  —  F(c)=BiLsen0^o=0  —   R- B

03- O campo magnético  é dirigido do pólo norte para o pólo sul  —  nos trechos BC e AD a força magnética é nula (B e i são paralelos)  —  usando a regra da mão esquerda as forças nos trechos AB (F_AB) e CD (F_CD) estão indicadas na figura

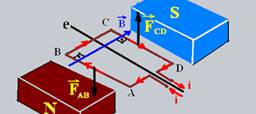
A intensidade das forças que agem sobre BC e AD é zero (B e i são paralelos, θ=0^o)  —  Intensidade de F_AB  —  F_AB=F_CD=BiLsenθ=2.10^-3.10.0,2  —  F_AB=F_CD=4,0.10^-3T  

04- Para a inversão no sentido da força que atua sobre o fio deve-se inverter o sentido da corrente OU o sentido do campo magnético  —  R- B

05- Para que a barra metálica condutora PQ esteja em equilíbrio, seu peso (vertical e para baixo)

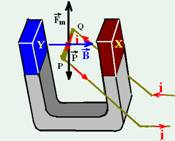
deve ser anulado pela força magnética que deve ser vertical e para cima  —  usando a regra da mão esquerda,  está indicado na figura acima, saindo do pólo norte e indo para o pólo sul  —  X é um pólo norte e Y é um pólo sul.

06-  Cálculo da intensidade da corrente elétrica no nos fios e no condutor cilíndrico  —  R_eq=0,10 + 0,02  —  R_eq=0,12Ω  —  R_eq=U/i  —  0,12=4,8/i  —  i=4,8/0,12  —  i=40 A  —  como o condutor cilíndrico fica em equilíbrio, a força magnética F_m deve ser vertical e para cima para equilibrar o peso que é vertical e para baixo  — F_m=P  —  BiLsenθ=mg  —  B.40.0,10.1=0,005.10  —  B=0,05/4  —  B=0,0125T  —  R- A  

07- Força magnética vertical e para baixo  —  F_m=BiLsen90^o=0,1.10.0,4.1  —  F_m=0,4N  —  força gravitacional vertical e para baixo  —  P=mg=0,03.10  —  P=0,3N  —  força elástica vertical e para cima  —  F_e=k.x  —  F_e=10x  —  F_m + P = F_e  — 

0,4 + 0,3=10x  —  x=0,7/10=0,07m  —  x=7,0cm

08- a) Se a chave está aberta não passa corrente pelo fio e a força magnética sobre ele é nula e assim, a força de tração no fio condutor rígido (indicação do dinamômetro) é igual ao peso do fio  —  P=m.g=0,2.10  —  o dinamômetro indica T=2,0N

b) Com a chave fechada, circula no fio condutor rígido uma corrente elétrica i e surge sobre o fio uma força magnética para cima, que deve anular o peso do fio, pois o dinamômetro indica zero  — F_m=P  —  i e B são perpendiculares – θ=90^o  —  B.i.ℓ.sen90^o=2  —  1.i.0,2=2  —  i=10A  —  regra da mão esquerda F_m para cima, B entrando, i deve ter direção horizontal e sentido para a direita.

c) R=U/i  —  6=U/10  —  U=60V

09- Com a tensão elétrica desligada a força elástica aplicada por cada mola deve equilibrar o peso do fio  —  2F_e=P  —  2.k.x=P  —  2.5.2.10^-3=P  —  P=20.10^-3  —  P=0,02N

10- Veja o esquema abaixo onde foi usada a regra da mão esquerda

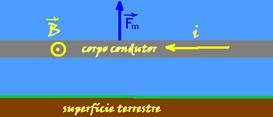
R- A

11- Como as intensidades de B e de i são constantes, então quem varia é o comprimento L de cada trecho do fio, tracionados  por forças diferentes, as quais, em cada trecho tem a direção e sentido fornecidos pela regra da mão esquerda e esquematizados na

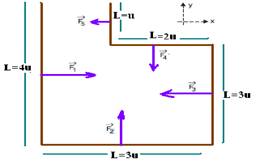
figura  —  F₁=Bi4u  —  F₂=Bi3u  —  F₃=Bi3u  —  F₄=Bi2u  —  F₅=Biu  —  na direção X  —  F_RX=F₁ – F₃ –F₅=4Biu – 3Biu – Biu  —  F_RX=0  —  na direção Y  —  F_RY=F₂ – F₄=3Biu – 2Biu  —  F_RY=Biu  —  R- C

12- a) Quando o gerador é ligado, com a chave A aberta e a chave C fechada, a corrente elétrica circula apenas no trecho OO’P₃P₄  —  quando a massa M=0,008kg é pendurada no ponto K, meio do segmento P₃P₄, para o sistema permanecer em equilíbrio , a força magnética F_m deve equilibrar o peso da massa M=0,008kg. ou seja, deverá ser vertical e para cima (veja figura) com

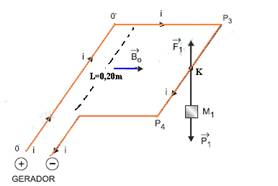
direção e sentido fornecidos pela regra da mão esquerda —  F₁=P₁=m₁.g  —  F₁=0,008.10  —  F₁=0,08N

b) Ainda nas condições anteriores  —  F₁=BiL  —  0,08=B.2.0,20  —  B=0,2T

c) Fechando a chave A e abrindo a chave C a corrente elétrica circulará nos trechos P₁P₂P₃P₄, com as forças  e  – colocadas nos pontos médios K (de P₃P₄) e N (de P₁P₂) e que foram obtidas pela regra da mão esquerda  —  nessas condições a espira tenderá a girar em torno de OO’  —   como nos trechos P₁P₂ e P₃P₄ B, L e i são os mesmos, as intensidades de  , – e  são

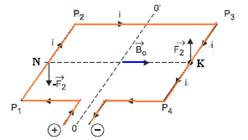
iguais e valem F=0,08N  —  para que se equilibre o binário ( e  –) você deve provocar um torque no sentido oposto, ou seja,

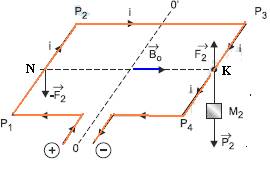
 deve pendurar no ponto K uma massa M₂  que seja o dobro de M1  —  M₂=0,16kg  —  (veja figura)

13- A corrente i no circuito principal (no sentido anti-horário) faz surgir na barra condutora uma força magnética de intensidade F, vertical e para baixo (fornecida pela regra da mão esquerda) que comprime para baixo as molas, estabelecendo contato com o circuito secundário anexo, fechando o circuito e acendendo a lâmpada  —  a força eletromotriz mínima E faz com que as forças elásticas das molas e a força magnética se equilibrem  —  força magnética  —  F_m=BiLsenθ=BiLsen90^o  —  F_m=BiL  —  força elástica de uma mola  —  F’_e=kx  —  como são duas molas F_e= 2F’_e=2kx  —  F_e=2kx  —  F_m=F_e  —  BiL=2kh (I)  —  R_eq=U/i  —   

2R=E/i  —  i=E/2R (II)  —  (II) em (I)  —  B(E/2R)L=2kh  —  0,01.E.2.0,05.0,3=2.2.0,03  —  E=4,0V  —  R- E

14- Quando o músculo cardíaco se contrai surge uma corrente elétrica no fio  —  no caso, i saindo do plano da página  — o campo magnético  é vertical e para baixo  —  regra da mão esquerda  —  a força magnética  será horizontal e para a direita  —  F_m=BiL (direta mente proporcional a i)  —  R- A

15- Utilizando a regra da mão esquerda  —  indicador – indica o campo magnético , horizontal para a direita (do pólo norte para

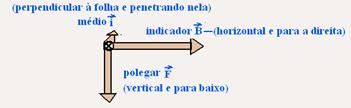
 o pólo sul)  —  médio – indica a corrente elétrica i (entrando na folha de papel)  —  polegar – indica a força magnética   — 

observe na figura que o polegar está indicando que  é vertical e para baixo

R- A

16- Observe no exercício anterior que a força magnética  que age sobre o fio é vertical e para baixo, juntamente com o peso   —a força elástica  age sobre o fio puxando-o para cima  —  intensidade de   —  F_m=B.i.ℓ.senθ=5.10^-1.4.10^-1.2.sen90^o  — 

F_m=40.10^-2.1  —  F_m=0,4N  —  intensidade do peso   —  P=mg=6.10².10^-3.10  —  P=6N  —  a intensidade da força resultante sobre o fio, vertical e para baixo vale  —  F_R=6.0 + 0,4  —  F’_R=6,4N  —  a força elástica , vertical e para cima vale  —  F_e=kx  —  F_e=2.10².x  —  como o sistema está em equilíbrio a intensidade da força resultante é nula, ou seja  —  F_e=F’_R  —  2.10²x=6,4  —  x=6,4/2.10²  —  x=3,2.10^-2m  —  R- D

 

17- a) Como a barra metálica possui resistência ôhmica R=5Ω e o gerador resistência ôhmica interna r=5Ω e eles estão associados em série, a resistência equivalente  vale R_eq=5 + 5=10Ω  —  R_eq=U/i  —  10 = U/5  —  U=ε=50V  —  potência elétrica dissipada pela barra metálica  —  P_d=R_barra.i² = 5.5²  —  P_d=125W.

b) Conhecendo a direção e sentido do campo magnético (perpendicular à folha de papel e penetrando nela) e da corrente

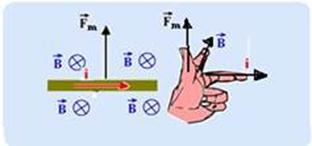
elétrica i (horizontal e para a direita), utilizando a regra da mão esquerda você localiza a força magnética (vertical e para cima – veja figura acima)  —  a intensidade dessa força magnética vale  —  F_m=B.i.ℓ.senθ=0,4.5.0,5.sen90^o=1.1  —  F_m=1N  —  sobre a barra agem as forças  —  força magnética  (vertical e para cima), força elástica  aplicada pela mola (vertical e para cima) e a força peso  (vertical e para baixo)  —  como o enunciado afirma que o sistema está em equilíbrio, a intensidade da força resultante  sobre a barra deve ser nula  —  assim, F_e + F_m = P  —   k.x + 1 = m.g  —  80.x + 1 = 5  —  x=4/80  —  x=0,05m ou x=5.10^-2m.

 

Voltar para os exercícios