Campo magnético – Resolução comentada
Resolução comentada dos exercícios de vestibulares sobre
Campo magnético originado por um condutor retilíneo extenso percorrido por corrente elétrica
01- Usando a regra da mão direita — R- D
02- Observe na expressão B=μ.i/2πr que B é inversamente proporcional a r — R- E
03- B=μi/2πr=4π.10-7.5/2π0,2 — B=5,0.10-6T — regra da mão direita — penetrando na folha de papel — R- E
04- O polo norte da bússola está no sentido da orientação do campo magnético, fornecida pela regra da mão direita — R- C
05- R- B — veja teoria
06- Regra da mão direita — R- C
07- Pela regra da mão direita o sentido de![]() é para fora da página (saindo dela) e pela expressão matemática B=μ.i/2πr, a intensidade de B é inversamente proporciona à distância r — R- A
é para fora da página (saindo dela) e pela expressão matemática B=μ.i/2πr, a intensidade de B é inversamente proporciona à distância r — R- A
08- Observe na expressão B=μ.i/2πr que i é diretamente proporcional a B — se i triplica, B também será triplicado — R- D
09- Quando não passa corrente elétrica pelo fio, a agulha da bússola indica a direção norte sul magnética da Terra — quando passa corrente elétrica no fio, surge outro campo magnético devido ao fio e a agulha da bússola irá indicar outra posição que é obtida pela soma vetorial dos dois campos magnéticos, ou seja, ![]() =
= ![]() +
+ ![]() — a esfera permanece na mesma posição, pois está em repouso — R- A
— a esfera permanece na mesma posição, pois está em repouso — R- A
10- Quando não passa corrente elétrica pelo fio, a agulha da bússola indica a direção norte sul magnética d Terra — quando passa corrente elétrica no fio, surge outro campo magnético devido ao fio e a agulha da bússola irá indicar outra posição queé obtida pela soma vetorial dos dois campos magnéticos, ou seja, ![]() =
= ![]() +
+ ![]() — R- B
— R- B
11- Colocando, pela regra da mão direita em cada região, os campos originados por cada fio, as regiões onde eles não podem se anular
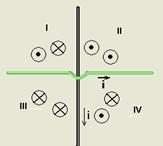
(soma vetorial), são as II e III — R- C
12- Observe na expressão B=μ.i/2πr que, se i duplica, B duplica e que se r for reduzida à metade B também duplica — R- B
13- Colocando, pela regra da mão direita em cada região, os campos originados por cada fio, as regiões onde eles tem sentidos opostos
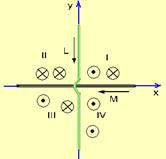
(um saindo da folha e o outro entrando na folha) são I e III — R- E
14- O vetor campo magnético criado pela corrente elétrica é ortogonal a ela e com sentido fornecido pela regra da mão direita — observe que quando a bússola está sobre o condutor o campo magnético é orientado para baixo (onde indica o pólo norte da bússola) e quando a bússola está sob o condutor o campo magnético é orientado para cima (onde indica o pólo norte da bússola) — R- E
15- Pela regra da mão direita o campo magnético criado pelo fio tem direção vertical e sentido para baixo (para onde indica o polo norte da agulha) e o campo magnético da Terra tem direção norte-sul, podendo estar para cima ou para baixo, mas como i é muito alta, ![]() , o campo magnético resultante sempre terá direção vertical e sentido para baixo — R- B
, o campo magnético resultante sempre terá direção vertical e sentido para baixo — R- B
16- a) O fio está no centro da figura e a corrente tem sentido “saindo do papel”.
b) Observe a figura a seguir.
17- Pela regra da mão direita C1 origina em P um campo magnético vertical e para cima e C2origina em P um campo magnético
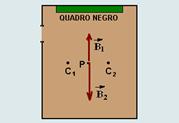
vertical e para baixo — como a intensidade de B2 é maior que a de B1, pois B2 tem maior corrente que B1, o campo magnético resultante é vertical e para baixo — R- A
18- Se i1 estiver saindo e i2 entrando na folha do papel ![]() e
e ![]() estarão como na figura e devem se
estarão como na figura e devem se
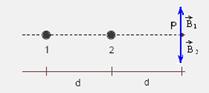
anular, ou seja, B1=B2 — μi1/2π.2d= μi2/2π.d — i1/2=i2 — i1=2i2 — R- B
19- Veja figura abaixo:
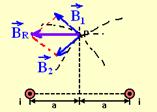
R- A
20- Observe a figura abaixo:
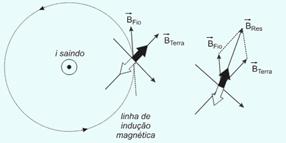
Enquanto a corrente era nula, a agulha da bússola indicava a orientação do campo magnético da Terra (![]() ) — quando o fio é ligado, surge nele corrente saindo do plano da página, que pela regra da mão direita, provocam linhas de indução magnética em torno do fio, no sentido anti-horário — o vetor indução magnética devido ao fio (
) — quando o fio é ligado, surge nele corrente saindo do plano da página, que pela regra da mão direita, provocam linhas de indução magnética em torno do fio, no sentido anti-horário — o vetor indução magnética devido ao fio (![]() ) é tangente às linhas de indução em cada ponto — a agulha da bússola orienta-se, então, no sentido do vetor indução magnética resultante —
) é tangente às linhas de indução em cada ponto — a agulha da bússola orienta-se, então, no sentido do vetor indução magnética resultante — ![]() =
= ![]() +
+ ![]() — R- A
— R- A
21- Observe na expressão Fm=μ.i1.i2.L/2.π.d que, duplicando a intensidade de cada corrente Fm ficará 4 vezes maior e que duplicando a distância Fm ficará 2 vezes menor — 4Fm/2=2Fm — R- C
22- Na experiência I as correntes possuem mesmo sentido e a força entre os fios é de atração diminuindo a distância entre eles e na experiência II, onde as corrente possuem sentidos contrários, a força entre eles é de repulsão, aumentando a distância entre eles — R- E
23- A força é de atração e tem a mesma intensidade, pois obedecem ao princípio da ação e reação — R- E
24- Veja resolução do exercício anterior — R- D
25- Observe as figuras abaixo onde estão as forças que agem sobre cada fio:
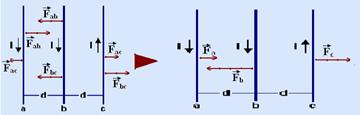
R- A
26- Como as correntes tem mesmo sentido irão atrair-se — como a força é inversamente proporcional à distância, se distância dobrar, a força cairá pela metade — R- D
27- A força é de repulsão pois a correntes tem sentidos contrários e é diretamente proporcional a i2

— Fm=μ.i.i.L/2.π.d — Fm=μ.i2.L/2.π.d — R- E
28- Pelas configurações das linhas de indução magnética você percebe que os fios se repelem e assim conduzem correntes de sentidos opostos. Essas forças tem sempre a mesma intensidade (par ação e reação) e a força que repele o fio da esquerda tem sentido da direita para a esquerda — R- D
29- Observe nas figuras abaixo a direção e o sentido da força magnética sobre o fio, desviando-o para a direita — a intensidade
dessa força é fornecida pela expressão Fm=B.i.l.senθ=B.i.l.sen90o — Fm=B.i.l — essa expressão afirma que a força magnética é diretamente proporcional à intensidade da corrente elétrica i que percorre o fio — R- A
30- (01) Errada. Cargas elétricas somente geram campo magnético quando estão em movimento.
(02) Correta. Corrente elétrica é formada pelo movimento de cargas elétricas.
(04) Errada. Se a corrente é alternada os pólos da bobina se alternam, diferente de um ímã que tem polos fixos.
(08) Correta.
(16) Errada.
R- (02 + 08) = 10
31-Observe o esquema abaixo — no triângulo OMP destacado à direita na figura — tgθ=(√3.a/2)/(a/2) — tgθ=√3 — θ=60o –
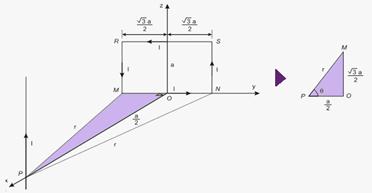
— no mesmo triângulo — sen θ=(3.a/2)/2r — √3/2=√(3.a)/2r — r=a — fios paralelos percorridos por correntes de mesmo sentido se atraem, e por correntes de sentidos opostos se repelem — para dois condutores de comprimento ℓ, distantes r entre si, percorridos por correntes I1 e I2, num meio onde a permeabilidade magnética é μ, a intensidade dessa força é — F=μI1.I2. ℓ/2πr — no caso desse exercício, I1=I2=I e ℓ=r=a — assim, sobre os lados RM e NS, a intensidade da força magnética, de acordo com a expressão acima, é dada por — F=μI2a/2πa — F=μI2/2π (I) — sendo os fios perpendiculares entre si, a força magnética é nula — assim o fio não exerce força sobre os lados MN e RS da espira — baseado na figura abaixo que mostra a situação vista de
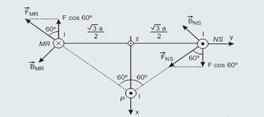
cima — usando a regra da mão direita nos lados NS e MR você encontra a direção e o sentido dos campos magnéticos ![]() e
e ![]() e, em seguida utilizando a regra da mão esquerda você localiza as forças
e, em seguida utilizando a regra da mão esquerda você localiza as forças ![]() e
e ![]() — observe que quem tende a provocar a rotação no sentido horário em torno do eixo z são as componentes Fcos60o de cada uma das forças
— observe que quem tende a provocar a rotação no sentido horário em torno do eixo z são as componentes Fcos60o de cada uma das forças ![]() e
e ![]() — cada uma dessas forças tem a mesma intensidade fornecida pela equação (I) acima — F=μI2/2π (I) — a distância do ponto de aplicação das forças até o eixo z vale √3/2.a — Mresultante=2.Fd=2.(Fcos600.√3/2.a) — Mresultante=μI2/2π.0,5.√3.a — Mresultante=√3μI2.a/4π
— cada uma dessas forças tem a mesma intensidade fornecida pela equação (I) acima — F=μI2/2π (I) — a distância do ponto de aplicação das forças até o eixo z vale √3/2.a — Mresultante=2.Fd=2.(Fcos600.√3/2.a) — Mresultante=μI2/2π.0,5.√3.a — Mresultante=√3μI2.a/4π
32- A intensidade do campo magnético produzido por um fio retilíneo é dado pela expressão B=μoi/2πr — observe que ela é diretamente proporcional à corrente elétrica. Sendo assim, se duplicarmos a corrente, duplicaremos também a intensidade do campo — R- D
33- Observe a figura abaixo, onde, pela regra da mão direita você obtém os vetores ![]() no fio da
no fio da
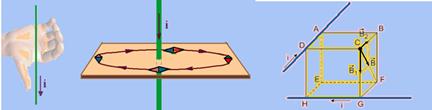
aresta DA e ![]() no fio da aresta GH — como esses dois campos têm a mesma intensidade, pois B=μi/2r o campo magnético resultante,
no fio da aresta GH — como esses dois campos têm a mesma intensidade, pois B=μi/2r o campo magnético resultante, ![]() , tem o sentido CF, indicado na figura — R- C
, tem o sentido CF, indicado na figura — R- C
34- 01. Falsa — as figuras abaixo mostram os campos magnéticos originados, usando a regra da mão direita, no fio 4, pelos fios 1
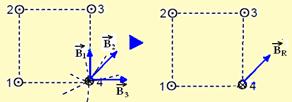
mão direita, no fio 4, pelos fios 1 (![]() ), 2 (
), 2 (![]() ) e 3 (
) e 3 (![]() ) — em seguida, somando-os vetorialmente foi obtido o vetor campo magnético resultante que aponta para o nordeste.
) — em seguida, somando-os vetorialmente foi obtido o vetor campo magnético resultante que aponta para o nordeste.
02. Correta — observe na figura abaixo a utilização da regra da mão esquerda no fio 4 que fornece a força magnética ![]()
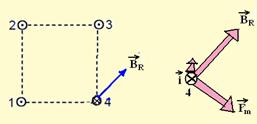
indicando para o sudeste.
04- Falsa — observe que as correntes elétricas nos fios 1 e 3 tem o mesmo sentido e que, dois fios condutores retilíneos, paralelos e próximos um do outro, sofrem forças de atração se as correntes que os percorrem tiverem mesmo sentido.
08- Correta — observe na expressão Fm=μ.i1.i2.L/2.π.d que fornece a intensidade da força magnética entre dois fios longos e próximos, separados pela distância d, que Fm é inversamente proporcional à d — como a distância entre 2 e 3 é menor que a distância entre 1 e 3, a afirmativa está correta.
16- Correta — observe atentamente a seqüência das figuras abaixo — como BR > B4, o campo magnético resultante aponta para
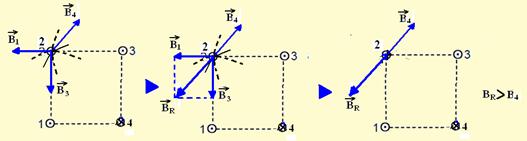
o sudoeste.
32- Falsa — aponta para o nordeste — veja a figura abaixo.
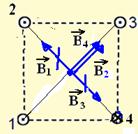
R- (02 + 08 + 16)=26
35- a) A figura abaixo mostra o campo magnético produzido pela corrente i1 e a força de atração que tal campo produz no fio onde
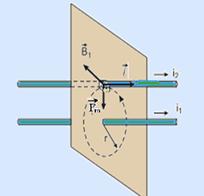
circula i2 — campo ![]() produzido por i1 no fio 2 (regra da mão direita) — B1=μo.i1/2πr (I) — força de atração
produzido por i1 no fio 2 (regra da mão direita) — B1=μo.i1/2πr (I) — força de atração ![]() sobre o fio 2, fornecida pela regra da mão esquerda — Fm=Biℓsen90o — Fm=Bi2ℓ (II) — (I) em (II) — Fm=μoi1i2ℓ/2πr — Fm/ℓ= μoi1i2/2πr — aplicando a lei de Ohm V=R.i — fio 1 — 1=1.i1 — i1=1 A — fio 2 — 1=2i2 — i2=0,5 A — substituindo os valores na equação Fm/ℓ= μoi1i2/2πr — Fm/ℓ=4π.10-7.1.0,5/2π.0,1 — Fm/ℓ=10-6 N/m
sobre o fio 2, fornecida pela regra da mão esquerda — Fm=Biℓsen90o — Fm=Bi2ℓ (II) — (I) em (II) — Fm=μoi1i2ℓ/2πr — Fm/ℓ= μoi1i2/2πr — aplicando a lei de Ohm V=R.i — fio 1 — 1=1.i1 — i1=1 A — fio 2 — 1=2i2 — i2=0,5 A — substituindo os valores na equação Fm/ℓ= μoi1i2/2πr — Fm/ℓ=4π.10-7.1.0,5/2π.0,1 — Fm/ℓ=10-6 N/m
b) Expressão do efeito fotoelétrico — Wo=h.fo — h.fo– energia que um fóton transporta — Wo – função trabalho do material — v=c=λo.fo — fo=c/λo — Wo=h.c/λo — 3ev=6.10-34.3.108/λo — 3×1,6.10-19=18.10-26/λo — λo=3,75.10-7m — λ < 3,7.10-7m
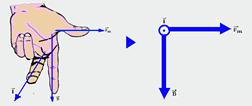
36- Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida
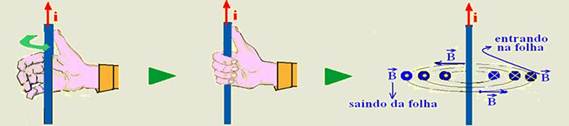
você fecha a mão para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
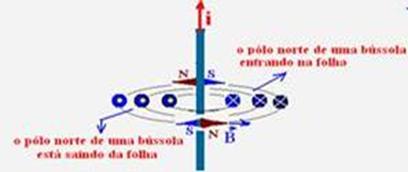
O pólo norte de uma bússola indica sempre o sentido das linhas de indução fornecido pela regra da mão direita.
R- D
37- Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita — esse sentido de
, é a regra da mão direita — esse sentido de![]() depende do sentido da corrente que o origina — você coloca o
depende do sentido da corrente que o origina — você coloca o
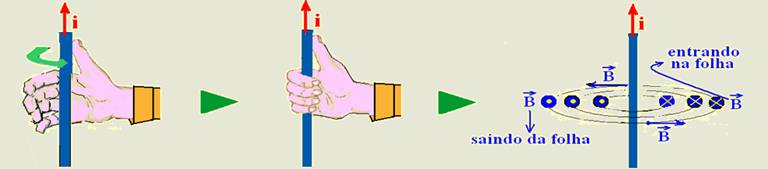
polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura) — observe na terceira figura que
(terceira figura) — observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto — no caso do exercício, utilizando essa regra os campos magnéticos gerados terão
é sempre tangente às linhas de indução em cada ponto — no caso do exercício, utilizando essa regra os campos magnéticos gerados terão
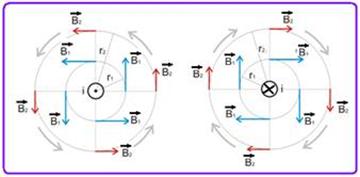
os aspectos indicados na figura e, se você observá-los atentamente verificará que a única alternativa correta é a D.
R- D
38-(UEPA)
Campo magnético![]() criado por um fio condutor reto percorrido por corrente elétrica — na figura 2, o fio condutor da figura 1 está colocado perpendicularmente à folha a esta folha de papel.
criado por um fio condutor reto percorrido por corrente elétrica — na figura 2, o fio condutor da figura 1 está colocado perpendicularmente à folha a esta folha de papel.
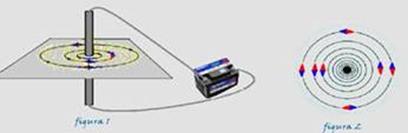
O sentido do campo depende do sentido da corrente no fio. A agulha da bússola se alinha com esse campo.
![]() Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética
Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética ![]() ou vetor campo magnético
ou vetor campo magnético![]() , é a regra da mão direita. Esse sentido de
, é a regra da mão direita. Esse sentido de![]() depende do sentido da corrente que o origina.
depende do sentido da corrente que o origina.
Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão para pegar o
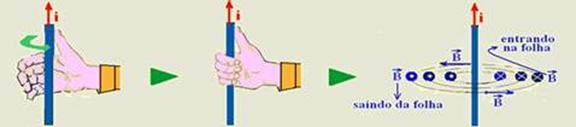
fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor![]() (terceira figura). Observe na terceira figura que
(terceira figura). Observe na terceira figura que ![]() é sempre tangente às linhas de indução em cada ponto.
é sempre tangente às linhas de indução em cada ponto.
Comprova-se experimentalmente que a intensidade do campo magnético![]() depende da intensidade da corrente elétrica i, da distância r do fio até o ponto (P) onde se quer o campo magnético e do meio onde o condutor se encontra. Essa dependência de
depende da intensidade da corrente elétrica i, da distância r do fio até o ponto (P) onde se quer o campo magnético e do meio onde o condutor se encontra. Essa dependência de![]() com o meio é fornecida pela constante μ que recebe o nome de permeabilidade magnética do meio e no vácuo ela vale μo=4π.10-7T.m/A. Matematicamente:
com o meio é fornecida pela constante μ que recebe o nome de permeabilidade magnética do meio e no vácuo ela vale μo=4π.10-7T.m/A. Matematicamente:

No caso do exercício — μ==4π.10-7T.m/A — r=16m — i=2,4.103 A — B=μ.i/2πr=4π.10-7.2,4.103/2π.16 — B=(2,4/8).10-4T — B=3.10-5T — B/Bo=3.10-5/3 — B/Bo=10-5 — R- C
