Resolução comentada dos exercícios de vestibulares sobre
Campo Magnético gerado por uma espira circular ou por um solenoide
01- R- A — veja teoria
02– 01- Correta — veja teoria
02. Falsa — veja 1
04. Falsa — tem sentidos opostos, fornecidos pela regra da mão direita
08- Falsa — veja na expressão B=μ.i/2R que i é diretamente proporcional a B — se i dobra, B também dobra
16- Falsa — veja na expressão B=μ.i/2R que R é inversamente proporcional a B — se R dobra, B cai pela metade
32- Falsa — a direção não se altera, mas o sentido sim
R- 1
03- Usando a regra da mão direita — o campo magnético
04- Os vetores indução magnética devem se anular e, para isso, as correntes nas espiras circulares devem ter mesma intensidade e sentidos contrários — R- B
05- A intensidade do campo magnético no centro da espira é fornecido por Be=μi/2πR e o campo magnético no centro da esfera originado pelo fio retilíneo é fornecido por Bf=μi1/2R — para que o campo resultante seja nulo — Be=Bf — μi/2πR= μi1/2R — i=i1/2π — i/i1=2π — o campo magnético
06- A direção e sentido do campo magnético originado no centro da espira pelo fio retilíneo é fornecida pela regra da mão direita e tem direção perpendicular ao papel e entrando nele (figura 1) e tem intensidade Bf=μif/2πR — Bf=62,8μ/2πR — para que o campo magnético resultante no centro da espira seja nulo, o campo magnético aí deve ser perpendicular ao papel e saindo dele e, para que isso ocorra o sentido da corrente elétrica deve ser anti-horário (fornecido pela regra da mão direita –
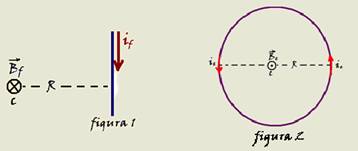
figura 2) e deve ter intensidade — Be=μ.ie/2R — como o campo magnético resultante deve ser nulo — Be=Bf — μ.ie/2R=62,8μ/2πR — ie=62,8/π — ie≈20 A e sentido anti-horário
07– a) Observe na figura abaixo que, se Rtotal=8Ω — Ri1=8/4=2Ω e Ri2=3.8/4=6Ω — observe também
que a diferença de potencial UAB=VA – VB é a mesma para os dois trechos — UAB=Ri1.i1=2i1 — UAB=Ri2.i2=6.i2 — 2i1=6i2 — i1=3i2 (I) — i1 + i2=4 — i1=4 – i2 (II) — (II) em (I) — 4 – i2=3i2 — i2=1 A — i1=3 A
b) Pela regra da mão direita a corrente elétrica i1 originará no centro da espira um
saindo da folha de papel — B1=(1/4)μi1/2R=μ.3/4.2R — B1=3μ/8R — B2=(3/4)μi2/2R=3μ/4.2R — B2=3μ/8R — observe que B1=B2 — como eles tem sentidos opostos e mesma intensidade, eles se anulam — o campo magnético no centro da circunferência será nulo.
08- Os dois campos B1 e B2 devem se anular — B1=μi1/2R1 — B1=μi1/0,8R2 — B2=μi2/2R2 — B1=B2 — μi1/0,4R2=μi2/2R2 — I1/i2=0,4 — R- A
09- a) A espira produz em C um campo magnético B2 perpendicular à folha e saindo dela (regra da mão direita) — para que os campos se anulem a corrente no fio deve ser da direita para a esquerda, produzindo em C, um campo perpendicular à folha e entrando nela (regra da mão direita)
b) espira — B1=μi1/2R — fio — B2= μi2/2πR — B1=B2 — μi1/2R= μi2/2πR — i2/i1=π=3
10- Esquematizando a situação na figura abaixo, e, com a corrente no sentido anti-horário vista pelo observador O, utilizando a regra
da mão direita, a espira se tornará um pequeno imã com pólo norte e pólo sul indicados:
I. Correta — elas se repelem (pólos de mesmo nome) e estas forças constituem um par ação e reação (mesma intensidade, mesma direção mas sentidos opostos).
II. Falsa — a força entre eles é de repulsão
III. Fa=Fi — ma.aa=mi.ai — ma.aa=2ma.ai — aa=2.ai — Correta
IV. Falsa
R- A
11- R- C — veja teoria
12- Veja figura abaixo:
R- B
13- Usando a regra da mão direita as configurações das linhas de indução do campo magnético do
solenoide estão indicadas na figura — a agulha magnética tem seu polo norte sempre no sentido das linhas de indução — R- B
14- Fechando a chave, colocando a corrente no sentido indicado (sai do pólo sul do gerador) e aplicando a regra da mão direita você verifica que as linhas de indução do campo magnético gerado pelo eletroímã saem do pólo norte, à esquerda e entram no pólo sul,
à direita — o imã será atraído — pólos opostos se atraem — R- B
15- Se uma corrente elétrica circular pelas espiras, a barra de ferro se comportará como um magneto (imã) — R- D
16-
00. Verdadeira — a pilha fornece corrente contínua.
01. Falsa — veja teoria.
02. Falsa — só surgirá campo magnético se a corrente nas espiras for corrente contínua.
17- a) Quando você liga as extremidades do fio aos pólos da pilha, este passa a ser percorrido por uma corrente elétrica que, por sua vez, gera um campo magnético ao seu redor. Este campo magnético gerado pela corrente elétrica imantará a haste e ela, comportando-se como um ímã, passará a atrair pequenos objetos de ferro ou aço.
b) Pela regra da mão direita, o pólo norte é a extremidade da direita, de onde saem as linhas de indução do campo magnético.
c. A extremidade da direita passa a ser o pólo sul e a da esquerda o pólo norte, ou seja, quando se inverte o sentido da corrente elétrica, inverte-se também a polaridade.
18- R- C — veja teoria
19– I. Observe na expressão B=μ.i.(N/L) — (N/L) é o número de espiras por unidade de comprimento — Correta
II. A intensidade do campo magnético aumenta — Falsa
III. Correta — observe na expressão B=μ.i.(N/L) que i é proporcional a B — correta
R- E
20- Pela regra da mão direita a extremidade esquerda do solenóide é um pólo sul — pólos de nomes opostos se atraem e o carrinho se aproximará do solenóide — R- A
21- I- Pela regra da mão direita você verifica que está correta.
II- Falsa — imã atrai ferro independente da polaridade.
III- Falsa — o vetor indução magnética no interior do imã é proporcional a corrente elétrica i que irá aumentar.
R- D
22- a) Aplicando a função do gerador — U=E – r.i — 8=E – 5.200.10-3 — 8=E – 1 — E=9,0V
b) B=4.π.10-7.(200/0,2).200.10-3=4.π.10-7.103.2.10-1 — B=8,0π.10-5T
23- a) B=4π.10-7.(2.000/0,5).3 — B=48.π.10-4 — B=4,8.π.10-3T
b) Como ele é lançado paralelamente ao eixo, o ângulo entre
24- Esquematizando a situação (figura) — a barra AB só pode estar imantada pois N atrai A (que é polo sul) já que pólos opostos se atraem e, consequentemente B será um polo norte — como S e B são repelidas pela bobina, esta ao ser percorrida por corrente i
originará em sua parte superior um pólo S e na inferior um polo norte — R- D
25- Quando se aumenta a resistência R, a intensidade da corrente elétrica na bobina diminui e consequentemente diminui também o campo magnético gerado por ela — R- B
26- a) Com a chave A aberta e a C fechada, para que o sistema permaneça em equilíbrio, segundo o
enunciado, uma pequena massa M1=0,008kg é colocada no ponto médio do segmento P3P4 — a corrente no circuito é no sentido horário e, aplicando a regra da mão esquerda no segmento P3P4, a força magnética sobre esse trecho de fio será vertical e para cima — P1=M1.g=0,008.10 —
P1=0,08N — no equilíbrio, F1=P — F1=0,08N
b) F1=iBoL — 0,08=2.Bo.0,2 — Bo=0,2T
c) Com a chave A fechada e C aberta o circuito ficará como o esquema indicado e a corrente elétrica
circulará no sentido horário — utilizando a regra da mão esquerda, a força magnética no trecho P1P2 será vertical e para baixo e no trecho P2P4, vertical e para cima — nos trechos P2P3 e P1P4 não haverá força magnética, pois neles, o campo magnético é paralelo à corrente elétrica —
Essas duas forças produzem um torque resultante, que tenta girar a espira em torno de OO’ no sentido horário — para a espira ficar em equilíbrio, você deve colocar uma massa M2numa dada posição de modo que ela produza um torque em sentido contrário (anti-horário), produzindo um torque resultante nulo — para que isso ocorra você pode colocar M2 em qualquer posição do
segmento P3P4, mas é mais coerente colocá-la no ponto médio do mesmo — as intensidades das forças magnéticas em cada fio são iguais (mesmo campo magnético, mesma corrente e mesmo comprimento-F=iBL) — para neutralizar o binário a força peso da massa M2 deverá ter o torque de mesmo módulo, mas sentido oposto, ou seja, a massa M2 deverá ser o dobro de M1 e logo M2 = 2.0,008 — M2= 0,016 kg.
27- (01) Errada — cargas elétricas somente geram campo magnético quando estão em movimento.
(02) Correta — corrente elétrica é formada pelo movimento de cargas elétricas.
(04) Errada — se a corrente é alternada os pólos da bobina se alternam, diferente de um ímã que tem pólos fixos.
(08) Correta.
(16) Errada.
R- (02 + 08) = 10
28- Observe que cada uma das faces do cubo percorrida por corrente comporta-se como uma espira quadrada — o campo magnético no centro do cubo gerado por uma face tem a mesma direção do campo no centro dessa face — o sentido desse campo é dado pela regra da mão direita (mão aberta, polegar no sentido da corrente, o sentido da corrente é fornecido pela “fechada” da mão,
passando pelo interior da espira) — para o cubo da figura (a) onde a corrente circula só na face esquerda, a Fig. 1 ilustra o vetor indução magnética citado no enunciado — para o cubo da figura (b) você deve analisar os campos gerados pelas faces opostas (pois têm a mesma direção) e confrontá-los quanto ao sentido — a contribuição para a intensidade do campo magnético de cada aresta percorrida por corrente é B/4 — em cada um dos três casos abaixo, a intensidade do campo
magnético resultante vale BR=B/2 + B/2 — BR=B — observe pelo sistema de coordenadas fornecido que Bx = -B; By = B e Bz = B — R- B
29- a) Dados — μo = 1,3.10-6 T.m/A — N = 25.000 espiras — L = 0,65 m — i = 80 A — B= μo.n.i — n=número de espiras/unidade de comprimento=25.000/0,65 — B= μo(N/L).i=1,3.10-6x(25.000/0.65)x80 — B=4.0 T
b) Dados — m = 200 g = 0,2 kg — d = 2 mm = 2.10-3 m — aR = 0,5 m/s2 — g = 10 m/s2 — como o
imã sobe em movimento acelerado — Fm > P — pricípio fundamental da dinâmica — FR=m.aR — Fm – P = m.aR — Fm=0,2.10 + 0,2.0,5 — Fm=2,1N — cálculo do trabalho — W=Fm.d=2,1.2.10-3 — W=4,2.10-3J
30- Dados — N = 300 espiras/m — μo= 1,26.10-6T.m/A — i = 100 mA = 0,1 A; sen 62º = 0,88, cos 62º = 0,47 e tg 62º = 1,87 — pela regra da mão direita, o vetor indução magnética no interior do solenoide é horizontal para direita — o vetor indução
magnética terrestre é orientado para o norte — a figura ilustra esses vetores — nessa figura — tg
62o = BT/Bs — BT=Bstg62o — BT=N.μo.i.tg62o=300×1,26.10-6x0,1×1,87 — BT=7,1.10-5 T
31-(FMABC-SP)
Quando um solenoide é percorrido por corrente elétrica ele produz um campo magnético, campo este que cria um fluxo que atravessa as espiras — a capacidade de uma bobina (solenoide) em criar o fluxo magnético em seu interior em função da corrente que a percorre é denominada Indutância (símbolo L) medida em “henry” cujo símbolo é H — em função dos dados do exercício, a indutância é fornecida pela expressão matemática — L= μo.n2.S/d, sendo — μo – permeabilidade magnética do meio no interior do solenoide, no caso é o vácuo – μo=4π.10-7Tm/A — n – número de espiras – n=500 espiras — S – área da seção reta do solenoide (ou de cada espira) – S=πR2=3.(15.10-3)2 =3×225.10-6 — S=675.10-6m2 — d – comprimento do solenoide – d=25cm=25.10-2m — L= μo.n2.S/d, — L=4.3.10-7x(500)2×675.10-6/25.10-2 — L=81.10-5=0,81.10-3H — L=0,81mH — R- A
Voltar para os exercícios