Características das associações série e paralelo – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Características das associações série e paralelo
01- Como eles são idênticos, a tensão nos terminais de cada um deles é igual à metade da tensão
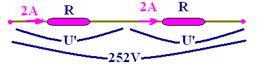
total — U1=U2=U’=252/2 — U’=126V — R=U’/i=126/2 — R=63Ω
02- Req=100 + 100 + 200 — Req=400Ω — Req=U/I — 400=U/0,5 — U=200V — P=i.U=0,5.200 — P=100W — ou — P=Req.i2 400.0,25=100W — R- E
03– Cálculo da corrente i, que é a mesma nos dois resistores — Req=U/i — 110=220/i — i=2ª — no resistor de 10Ω — R=U/i — 10=U/2 — R=20V
04- Resistência equivalente dos m resistores de resistência elétrica R1 — Req1=mR1 — idem — Req2=nR2 — Reqtotal=mR1 + nR2 — a corrente é a mesma em todos os resistores (associação série) e vale — Reqtotal=U/i — (mR1 + nR2)=U/i — i=U/(mR1 +nR2) — R- A
05- A tensão total é a soma das tensões de cada lâmpada — Ut=n.Ul — 117=n.15 — n=117/15 — n=7,8 — como a tensão nos terminais de cada lâmpada não pode ultrapassar 15V, deve-se selecionar 8 lâmpadas — R- D
06- Fechando a chave C, provoca-se um curto circuito nos terminais da lâmpada A, a corrente se desvia e ela se apaga. Assim, como a resistência total diminui, a corrente aumenta na lâmpada B aumentando seu brilho — R- A
07- lâmpada — P=i.U — 2,25=4,5.i — i=0,5A — como estão em série a corrente i também é 0,5A no resistor — no resistor — U=12 – 4,5=7,5V — R=U/i=7,5/0,5 — R=15 Ω — R- E
08- As lâmpadas terão correntes elétricas diferentes, pois possuem valores nominais diferentes — corrente em cada lâmpada — i100W=P/U=100/110=0,91A — i60W=60/220=0,28A — A corrente nessa associação série não pode exceder 0,28A, pois ultrapassaria a potência da lâmpada de menor potência (60W) — quando i=0,28A — P=iU — 100=0.28U — U=360V — R- E
09- Corrente na lâmpada — P=iU — 100=i.120 — i=5/6A — resistor — U=240 – 120=120V — P = iU=5/6.120 — 100W — R- B
10- U em cada lâmpada — U=110/20=5,5V — i em cada lâmpada — P=iU — 5=i.5,5 — i=1/1,1A — R=U/i=5,5/(1/1,1) — R- 6,05Ω
11- Req=(R + 100)=U/i — R + 100=110/0,5 — R=120Ω — R- C
12- Urede=U — UR=0,1U — UX=0,9U — iX=0,9U/X — iR=0,1U/R — série — iX=iR — 0.9U/X=0,1U/R — X=9R — R- C
13- I- Correta – 9 lâmpadas – 90W + 1 lâmpada de 5W — Pt=95W — P de cada lâmpada =95/10=9,5W
II- Correta – 9 lâmpadas – 90W + 1 lâmpada de 12W — Pt=102W — P de cada lâmpada =102/10=10,2W
R- A
14- Potência fornecida pela bateria — Pb=i.U=330.10-3.6 — Pb=1,98W — como o LED consome uma potência de 1,0W, sobra para o resistor R uma potência de 1,98 – 1,0 — PR=0,98W — PR=R.i2 — 0,98=R.(330.10-3)2 — R=98.10-2/(33.10-2)2 — R=9,0Ω — R- C
15- Resposta correta — circuito da figura III onde você consegue ligar a lâmpada, independentemente, em qualquer um dos interruptores — observe a seqüência abaixo:
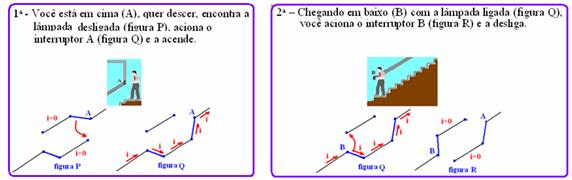
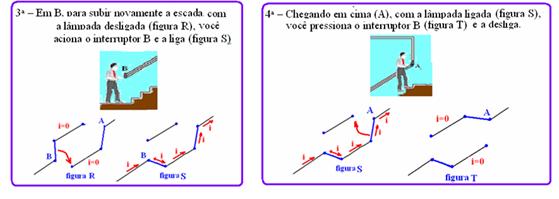
16- R- C — veja exercício anterior
17- Cálculo da corrente elétrica i no circuito que está em série — Req=2 + 5 + 8 + 5 — Req=20Ω — Req=U/i — 20=100/i —
i=5A — potência dissipada por R3 — P=R3.i2=8.(5)2 — P=200W — energia liberada pelo resistor imerso — W=P.Δt —
W=200.Δt (I) — energia necessária para transformar 200g de gelo a 0oC até água a 20oC — Q=mL + mcΔθ=200.80 + 200.1.(20 – 0)=16.000 + 4.000 — Q=20.000cal — 1cal=4J — Q=W=4.20.000 — W=80.000J (II) — igualando II com I —
200Δt=80.000 — Δt=400s — Δt=400s/60=6,7 — Δt=6,7 minutos
18- Observe que RA, RH e RP estão em série — o voltímetro ideal indica URA=10V —
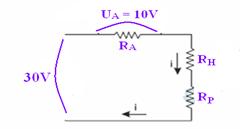
esquematizando o circuito — como estão todos em série, a corrente i é a mesma e vale — UA=RA.i — 10=106.i — i=10/106 — i=10-5A — UP=RP.i — UP=106.10-5 — UP=10V — Utotal=UA + UH + UP — 30=10 + UH + 10 — UH=10V — UH=RH.i — 10=RH.10-5 — RH=10/10‑5 — RH=106Ω — RH=1MΩ —
R- A
19- I- Falsa — quando uma das lâmpadas queima, no circuito em série, a corrente elétrica é interrompido e a outra lâmpada apaga.
II- Falsa — como as lâmpadas são idênticas, cada uma ficará sujeita a uma tensão de 110V e, a potência em cada uma delas ficará 4 vezes menor, ou seja, de 25W.
III- Falsa — como as lâmpadas são idênticas e cada uma delas ficará sujeita a uma tensão de 110V, elas estarão dentro das especificações, funcionando normalmente.
IV- Correta — como são idênticas, cada uma delas ficará com metade da tensão total que é de 220V, ou seja, cada uma ficará sujeita à tensão de 110V.
R- B
20- a)
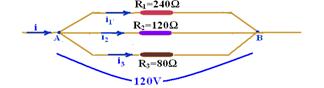
b) entre R1 e R2 — R’eq=240/3=80Ω — entre R’eq=80Ω e 80Ω — Req=80/2 — Req=40Ω — Req=U/i — 40=120/i — i=3A
c) R1=U/i1 — 240=120/i1 — i1=0,5A — R2=U/i2 — 120=120/i1 — i1=1,0A — R3=U/i3 — 80=120/i3 — i3=1,5A
21- Req=8/3Ω — Req=U/i — 8/3=U/3 — U=8V — i1=8/4=2A — i2=8/8=1A — R- D
22- R- A — veja resolução anterior
23- Cálculo da ddp U no resistor de 20Ω — U=R.i=20.4 — U=80V — cálculo de i no resistor de 10Ω — i=U/R=80/10=8A — cálculo de R — R=U/i=80/16=5Ω — R- A
24- Série — R1 + R2=6 — R1=6 – R2 — paralelo — R1.R2/(R1 + R2)=4/3 — (6 – R2).R2=(6 – R2 + R2) — R22 – 6R2 + 8=0 — √Δ=2 — R2=(6 ± 2)/2 — R’2=4Ω — R’’=2Ω — quando um é 2Ω, o outro é 4Ω e vice versa — R- C
25- a) Sim, é ôhmico — a resistência é constante — R=U/i=0,6/0,2=1,8/0,6=3,0/1,0=3,0Ω
b) P=U2/R=(9)2/3 — P=27W — W=P.Δt=27.300 — W=8.100J
c) Req1=R/3 — Req2=3R — como P=U2/Req — Req é inversamente proporcional a P, pois U é a mesma — aquele que aquece mais rapidamente a água é o que tem maior potência e consequentemente menor Req — associação I
26- a) Os aparelhos estão associados em paralelo e submetidos à mesma ddp de U=110V — P=iU — i=P/U — iaquec=2.200/110=20A — iferro=770/110=7A — ilâmpada=100/110=0,91A — ferro e lâmpada
b) n=15/0.91=16,5 — 16 lâmpadas
27- Req1=R1.R2/(R1 + R2) — Req1=U/i — R1.R2/(R1 + R2)=12/1 — R1.R2=12(R1 + R2) (I) — Req2=R2 — Req2=U/i — R2=12/0.4 — R2=30Ω (II) — (II) em (I) — R1.30=12(R1 + 30) — 18R1=360 — R1=20Ω
28- Todos os dispositivos elétricos de uma residência são associados em paralelo para que fiquem sujeitos à mesma diferença de potencial — aquecedor elétrico — W=P.Δt=200.1=200Wh — lâmpada — W=P.Δt=60.24=1.440W — R- E
29- Série — Reqs=10R — Reqs=U/i — 10R=120/0,05 — R=240Ω — paralelo — Reqp=R/10 — R/10=U/i — 240/10=120/i — i=5A — R- A
30- Se a ddp em seus terminais é constante as lâmpadas estão ligadas em paralelo — cálculo da corrente em cada lâmpada — P=iU — 60=i.120 — i=0,5A — n=15/0,5=30 lâmpadas
31- R e a lâmpada estão em paralelo e ambas sob ddp de 12V — lâmpada — P=iU — 6=il.12 — il=0,5A — Rl=U/i=12/0,5 — Rl=24Ω — Req=24R/(24 + R) — Req=U/i — 24R/(24 + R)=12/3 — 20R=96 — R=4,8Ω — R- E
32- Corrente em cada lâmpada — Req=U/i — 330=220/i — i=22/33 A — n=50/(22/33) — n=75 lâmpadas
33- a) P=iU=6/11.110 — P=60W
b) n=14/(6/11) — n=25 lâmpadas
34- O fio superior corresponde à um dos pólos da fonte e o inferior ao outro — observe atentamente as figuras — R- E
35- Observe que os pontos M,N,O,P,Q,R,S e T estão em curto circuito, então os 4 resistores estão em
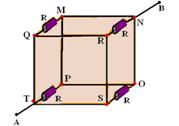
paralelo — Req=U/i — R/4=U/i — i=4U/R
36- corrente na lâmpada — Pl=il.U — 150=il.110 — il=214/15A — corrente no ferro — if=(15 – 214/15) — if=214/15A — Pf=if.U=214/15.110=1.570W — R- B
37- Chuveiro — ic=P/U=3.000/110=27,27A — geladeira — ig=400/110=3,63A — TV — iTV=150/110=1,36A — lâmpada — il=60/110=0,54A — faltam 30 – 27,7=2,3A — R- Lâmpada e TV
38-
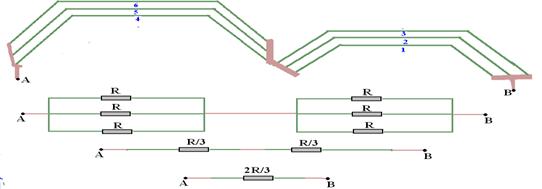
P=U2/Req — P=U2/(2R/3) — P=3U2/2R
39- Corrente total i no disjuntor — Pt=it.U — (1.400 + 920)=it.110 — it=21,1A — para que o disjuntor não desligue, a corrente elétrica mínima deve ser de 25 A — R- D
40- Lâmpada Q — PQ=U2/R — PR=U2/R — PS=(U/2)2/R=U2/4R — R- B
41– Dados — U = 12,4 V — i = 0,8 A — R1 = 0,2 Ω — r = 0,3 Ω — resistência equivalente da associação — U = Req.i — 12,4 = Req 0,8 — Req =12,4/0,8 — Req = 15,5 Ω — os valores das resistências estão em progressão aritmética (P.A.) —
an = a1 + (n – 1) r — Rn = R1 + (n – 1) r — Rn = 0,2 + (n – 1) 0,3 — Rn = 0,3 n – 0,1 — como os resistores estão associados em série, a resistência equivalente é a soma das resistências — soma dos n primeiros termos de uma P.A. — Sn =(a1 + an).n/2 — Req=(R1 + Rn).n/2 — 15,5={0,2 + (0,3n – 1).n}/2 — 31=0,3n2 + 0,1n — 3n2 + n – 310=0 — resolvendo a equação do 2º grau — n= (-1 ±√3.721)/6 — desprezando a resposta negativa — n= (-1 + 61)/6 — n=10 — R- A
42- (01) Correta — a potência elétrica é dado por: P = U2/R, sendo R a resistência elétrica — como a tensão é a mesma para as duas lâmpadas, a de maior potência apresenta menor resistência, ou seja, RA < RB — segunda lei de Ohm — R = ρL/S — nessa expressão, ρ é a resistividade do material; S é a área da secção transversal do filamento e L é o seu comprimento — se ambas forem do mesmo material e de mesmo diâmetro, a resistência será diretamente proporcional ao comprimento — RA < RB e
LA < LB.
(02) Correta — a intensidade luminosa é diretamente proporcional a potência luminosa emitida — potência luminosa de A — P’A= 30% de 100 = 0,3(100) = 30 W — potência luminosa de B P’B = 30% de 40 = 0,3(40) = 12 W — PA’/PB’=30/12=2,5
(04) Correta — a resistividade do filamento aumenta com a temperatura — o brilho de uma lâmpada é devido ao aquecimento de seu filamento a altas temperaturas — assim, quando desligadas, as lâmpadas apresentam menor resistividade, consequentemente, menor resistência.
(08) Falsa — quando estão associadas em série, ambas são percorridas pela mesma corrente elétrica — potência elétrica —
Pd = R i2 — como já concluído, RA < RB — então PA < PB — a intensidade luminosa deA é menor que a de B.
(16) Falsa — Como já justificado, RA < RB.
R- (01+ 02 + 04) = 07
43-


44- I. Correta — em toda associação série a intensidade da corrente elétrica é a mesma.
II. Cálculo da resistência, suposta constante, de cada lâmpada — P1=U2/R1 — 60=14.400/R1 — R1=240Ω — P2=U2/R2 —
100=14.400/R2 — R2=144Ω — resistor equivalente — Req=240 + 144 — Req=384Ω — corrente elétrica em cada resistor —

Req=U/i — 384=120/i — i=120/384 — i=0,3 A — cálculo da potência dissipada em cada lâmpada — P1=R1.i2=240.0,9 — P1=216W — P2=R2.i2=144.0,9 — P2=129,6W — a lâmpada 1 brilha mais, pois P1>P2 — correta
III. Falsa — veja justificativa anterior
45- A afirmativa errada é a C — veja seqüência abaixo — Req=0,72 + 1,44 + 1,44=3,6Ω — Req=U/i — 3,6=6/i — i=1,66 A

R- C
46- I. Falsa – Em uma ligação em série, a corrente elétrica que percorre as lâmpadas é a mesma. Assim, quando uma lâmpada queima, abre-se o circuito.
II. Falsa – Em uma ligação em série, a d.d.p. total é dividida para as duas lâmpadas. Assim, elas terão d.d.p de 110V, não funcionando como especificado no problema.
III. Falsa – A d.d.p. total é de 220V. Se colocarmos duas lâmpadas de 110V em série, funcionarão corretamente.
IV. Verdadeira – Como foi dito na afirmação II, cada lâmpada será submetida à d.d.p. de 110V.
R- B
47- Dados — R1 = R e R2 = 3R — resistência equivalente em série — Rs = R1 + R2= R + 3 R — Rs = 4 R — sendo E a força

eletromotriz da bateria ideal, a potência por ela fornecida nessa associação é — Ps=U2/Rs=E2/Rs — Ps=E2/4R (I) — resistência equivalente em paralelo — quando um é o triplo do outro, divide o maior por 4 — Rp=3R/4 — potência fornecida — Pp=U2/Rp=E2/Rp — Pp=E2/(3R/4) — Pp=4E2/3R (II) — dividindo membro a membro (I) por (II) — Ps/Pp=E2/4Rx3R/4E2 —
Ps/Pp=3/16
48- Os três resistores estão em paralelo, portanto e ddp é a mesma para o três, ou seja, U = 24 V — resistor R3 — P3=U2/R3 —
R3=242/32 — R3=18Ω — cálculo da Rrq — 1/Req=1/3 + 1/9 + 1/18 — Req=2Ω — R- E
49- Req=2.000/2 — Req=1.000Ω — P=U2/R=1002/1.000 — P=10W — R- D
50- P=iU — i=55/36 A — quando ligados a um mesmo fusível, a corrente dobra — I=2.(55/36) — I=3,05 A — para suportar essa corrente elétrica, o menor valor do fusível deve ser de 5 A, ou seja o laranja — R- C
51- A inversão de polaridade da pilha apenas inverte o sentido da corrente não alterando as demais características do circuito — observe na expressão P=U2/R que a potência é inversamente proporcional à resistência da lâmpada — assim, quanto menor a resistência do filamento, maior será a potência e consequentemente maior será o brilho — R- C
52- Os dois resistores estão em paralelo — Req=100/3Ω — Req=U/i=E/i — 100/3=E/1 — E=100/3V — R- B
53-

54- R- C — veja teoria
55)– Cálculo, pelos valores nominais, da corrente que deve circular por cada lâmpada — P=i.U — 6=i.10 — i=0,6 A — na associação paralelo a corrente total do fusível (atualmente disjuntor) de 6 A,
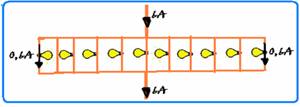
se divide, passando 0,6 A por cada lâmpada — n=6/0,6=10 lâmpadas — R- C.
56- Observe na figura que, como a bateria de 12V está ligada nos pontos A e B, os resistores de 5kΩ
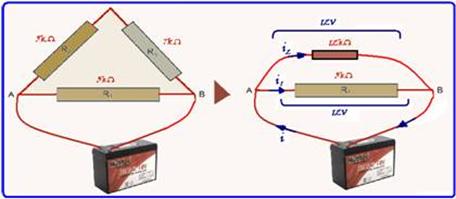
e de 7kΩ estão em série sendo substituídos por um único resistor de 12kΩ — agora os resistores de 12kΩ e de 3kΩ estão em paralelo e submetidos à mesma ddp da bateria de U=12V — i2=U/R=12/12k — i2=1mA — i1=U/R=12/3k — i1=4mA — i=i1 + i2=1 + 4=5mA — R- A
57- Todas devem estar associadas em paralelo, pois devem estar sob a mesma ddp de U=120V — cálculo de cada resistência — 3 lâmpadas — Po=U2/R1 — 300=14.400/R1 — R1=14.400/300 — R1=48Ω — chapa de sanduíche — Po=U2/R2 — 2.000=14.400/R2 — R2=14.400/2.000 — R2=7,2Ω — forno de micro-ondas — Po=U2/R3 — 1.500=14.400/R3 — R3=14.400/1.500 — R2=9,6Ω —
cálculo da resistência equivalente desses três resistores que estão associados em paralelo —
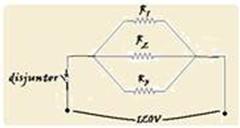
1/Req=1/48 + 1/7,2 + 1/9,6 —
1/Req= (69,12 + 460,8 + 345,6)/3 317,76 — Req≈3,8Ω — Req=U/itotal — 3,8=120/itotal — itotal=31,6 A — qualquer valor menor que 31,6 A desliga o disjuntor — R- E
58- Veja na figura como o circuito deve ser montado numa associação série — nessa associação, para que as lâmpadas
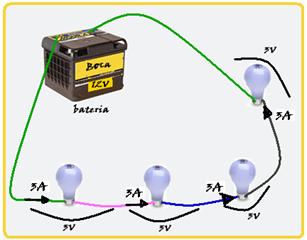
funcionem de maneira plena e eficiente, elas devem ser ligadas dentro das especificações (3V-9W) — assim, cada lâmpada deve ser percorrida por uma corrente de P=i.U — 9=3.i — i=3 A — a tensão total U=12V deve ser igual à soma das tensões de cada lâmpada, então você terá n=12V/3V=4 lâmpadas — resistência de cada lâmpada — R=U/i=3/3=1Ω — resistência equivalente — Req=4×1=4Ω — potência total do circuito — Pt=Ut.i=12.3 — Pt=36W — R- A.
59- Como esses resistores tem intensidades diferentes e são percorridos pela mesma corrente elétrica, eles estão

associados em série — resistência equivalente — Req=4 + 2=6Ω — Req=U/i — 6 = 12/i — i=2 A — R- D.
