Characteristics of series and parallel associations – EN Resolution
CHARACTERISTICS OF SERIES AND PARALLEL ASSOCIATIONS – RESOLUTION
Commented resolution of entrance exam exercises on
Characteristics of series and parallel associations
01- As they are identical, the voltage at the terminals of each of them is equal to half the voltage
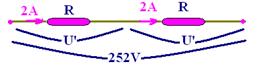
total — U 1 =U 2 =U’=252/2 — U’=126V — R=U’/i=126/2 — R=63Ω
02- R eq =100 + 100 + 200 — R eq =400Ω — R eq =U/I — 400=U/0.5 — U=200V — P=iU=0.5.200 — P=100W — or — P =R eq .i 2 400.0.25=100W — R- E
03 – Calculation of the current i, which is the same in both resistors — R eq = U/i — 110=220/i — i=2nd — in the 10Ω resistor — R=U/i — 10=U/2 — R=20V
04- Equivalent resistance of m resistors of electrical resistance R 1 — Req1 = mR 1 — idem — Req2 = nR 2 — Reqtotal = mR 1 + nR 2 — the current is the same in all resistors (series association) and is worth — Reqtotal = U / i — (mR 1 + nR 2 ) = U / i — i = U / (mR 1 + nR 2 ) — R – A
05- The total voltage is the sum of the voltages of each lamp — U t = nU l — 117 = n.15 — n = 117/15 — n = 7.8 — as the voltage at the terminals of each lamp cannot exceed 15V, 8 lamps must be selected — R- D
06- Closing switch C causes a short circuit in the terminals of lamp A, the current diverts and it goes out. Thus, as the total resistance decreases, the current increases in lamp B, increasing its brightness — R- A
07- lamp — P=iU — 2.25=4.5.i — i=0.5A — as they are in series the current i is also 0.5A in the resistor — in the resistor — U=12 – 4.5=7.5V — R=U/i=7.5/0.5 — R=15 Ω — R- E
08- The lamps will have different electric currents, as they have different nominal values — current in each lamp — i 100W = P/U=100/110=0.91A — i 60W =60/220=0.28A — The current in this series association cannot exceed 0.28A, as it would exceed the power of the lowest power lamp (60W) — when i=0.28A — P=iU — 100=0.28U — U=360V — R- E
09- Current in the lamp — P=iU — 100=i.120 — i=5/6A — resistor — U=240 – 120=120V — P = iU=5/6.120 — 100W — R- B
10- U in each bulb — U=110/20=5.5V — i in each bulb — P=iU — 5=i.5.5 — i=1/1.1A — R=U/i=5.5/(1/1.1) — R- 6.05Ω
11- R eq =(R + 100)=U/i — R + 100=110/0.5 — R=120Ω — R- C
12- U network =U — U R =0.1U — U X =0.9U — i X =0.9U/X — i R =0.1U/R — series — i X =i R — 0.9U/ X=0.1U/R — X=9R — R- C
13- I- Correct – 9 lamps – 90W + 1 5W lamp — P t = 95W — P of each lamp = 95/10 = 9.5W
II- Correct – 9 lamps – 90W + 1 12W lamp — P t = 102W — P of each lamp = 102/10 = 10.2W
A- A
14- Power supplied by the battery — P b =iU=330.10 -3 .6 — P b =1.98W — as the LED consumes a power of 1.0W, there is a power of 1.98 – 1.0 left for the resistor R — P R =0.98W — P R =Ri 2 — 0.98=R.(330.10 -3 ) 2 — R=98.10 -2 /(33.10 -2 ) 2 — R=9.0Ω — R- C
15- Correct answer — circuit in figure III where you can turn on the lamp, independently, with any of the switches — observe the sequence below:
16- R- C — see previous exercise
17- Calculation of the electric current i in the circuit that is in series — R eq = 2 + 5 + 8 + 5 — R eq = 20Ω — R eq = U/i — 20=100/i —
i=5A — power dissipated by R 3 — P=R 3 .i 2 =8.(5) 2 — P=200W — energy released by the immersed resistor — W=P.Δt —
W=200.Δt (I) — energy required to transform 200g of ice at 0 o C into water at 20 o C — Q=mL + mcΔθ=200.80 + 200.1.(20 – 0)=16,000 + 4,000 — Q=20,000cal — 1cal=4J — Q=W=4,20,000 — W=80,000J (II) — equating II with I —
200Δt=80,000 — Δt=400s — Δt=400s/60=6.7 — Δt=6.7 minutes
18- Note that R A , R H and R P are in series — the ideal voltmeter indicates U RA = 10V —
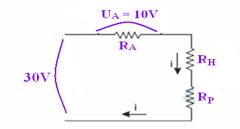
schematizing the circuit — as they are all in series, the current i is the same and is worth — U A = R A . i — 10=10 6 . i — i=10/10 6 — i=10 -5 A — U P =R P . i — U P =10 6 . 10 -5 — U P =10V — U total =U A + U H + U P — 30=10 + U H + 10 — U H =10V — U H =R H . i — 10=R H . 10 -5 — R H =10/10‑5 — R H =10 6 Ω — R H =1MΩ —
A- A
19- I- False — when one of the bulbs burns out, in the series circuit, the electric current is interrupted and the other bulb goes out.
II- False — as the lamps are identical, each one will be subject to a voltage of 110V and the power in each one will be 4 times lower, that is, 25W.
III- False — as the lamps are identical and each of them will be subject to a voltage of 110V, they will be within specifications and functioning normally.
IV- Correct — as they are identical, each of them will have half of the total voltage, which is 220V, that is, each one will be subject to a voltage of 110V.
R-B
20- a)
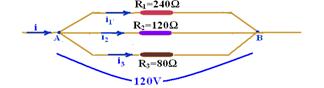
b) between R 1 and R 2 — R’ eq =240/3=80Ω — between R’ eq =80Ω and 80Ω — R eq =80/2 — R eq =40Ω — R eq =U/i — 40=120 /i — i=3A
c) R 1 =U/i 1 — 240=120/i 1 — i 1 =0.5A — R 2 =U/i 2 — 120=120/i 1 — i 1 =1.0A — R 3 =U /i 3 — 80=120/i 3 — i 3 =1.5A
21- R eq =8/3Ω — R eq =U/i — 8/3=U/3 — U=8V — i 1 =8/4= 2A — i 2 =8/8= 1A — R- D
22- R- A — see previous resolution
23- Calculation of ddp U in the 20Ω resistor — U=Ri=20.4 — U=80V — calculation of i in the 10Ω resistor — i=U/R=80/10= 8A — calculation of R — R=U/i =80/16= 5 Ω — R- A
24- Series — R 1 + R 2 =6 — R 1 =6 – R 2 — parallel — R 1 .R 2 /(R 1 + R 2 )=4/3 — (6 – R 2 ).R 2 =(6 – R 2 + R 2 ) — R 2 2 – 6R 2 + 8=0 — √Δ=2 — R 2 =(6 ± 2)/2 — R’ 2 =4Ω — R”=2Ω — when one is 2Ω, the other is 4Ω and vice versa — R- C
25- a) Yes, it is ohmic — the resistance is constant — R=U/i=0.6/0.2=1.8/0.6=3.0/1.0= 3.0Ω
b) P=U 2 /R=(9) 2 /3 — P=27W — W=P.Δt=27,300 — W=8,100J
c) Req1 =R/3 — Req2 = 3R — as P=U2 / Req — Req is inversely proportional to P, since U is the same — the one that heats the water faster is the one with the greatest power and consequently the lowest Req — association I
26- a) The devices are connected in parallel and subjected to the same ddp of U=110V — P=iU — i=P/U — i heater =2,200/110=20A — i iron =770/110=7A — i lamp =100/110=0.91A — iron and lamp
b) n=15/0.91=16.5 — 16 lamps
27- R eq1 =R 1 .R 2 /(R 1 + R 2 ) — R eq1 =U/i — R 1 .R 2 /(R 1 + R 2 )=12/1 — R 1 .R 2 = 12(R 1 + R 2 ) (I) — R eq2 =R 2 — R eq2 =U/i — R 2 =12/0.4 — R 2 =30Ω (II) — (II) in (I) — R 1 .30=12(R 1 + 30) — 18R 1 =360 — R 1 =20Ω
28- All electrical devices in a residence are connected in parallel so that they are subject to the same potential difference — electric heater — W=P.Δt=200.1=200Wh — lamp — W=P.Δt=60.24=1,440W — R- E
29- Series — R eqs =10R — R eqs =U/i — 10R=120/0.05 — R=240Ω — parallel — R eqp =R/10 — R/10=U/i — 240/10=120 /i — i=5A — R- A
30- If the ddp at its terminals is constant, the lamps are connected in parallel — calculation of the current in each lamp — P=iU — 60=i.120 — i=0.5A — n=15/0.5= 30 lamps
31- R and the lamp are in parallel and both under ddp of 12V — lamp — P=iU — 6=i l .12 — i l =0.5A — R l =U/i=12/0.5 — R l =24Ω — R eq =24R/(24 + R) — R eq =U/i — 24R/(24 + R)=12/3 — 20R=96 — R=4.8Ω — R- E
32- Current in each lamp — R eq = U/i — 330=220/i — i=22/33 A — n=50/(22/33) — n=75 lamps
33- a) P=iU=6/11,110 — P=60W
b) n=14/(6/11) — n=25 lamps
34- The upper wire corresponds to one of the poles of the source and the lower one to the other — observe the figures carefully — R- E
35- Note that points M, N, O, P, Q, R, S and T are short-circuited, so the 4 resistors are in
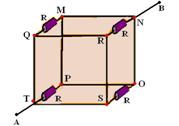
parallel — R eq =U/i — R/4=U/i — i=4U/R
36- current in the lamp — P l =i l .U — 150=i l .110 — i l =214/15A — current in the iron — i f =(15 – 214/15) — i f =214/15A — P f =i f .U=214/15.110=1.570W — R- B
37- Shower — i c =P/U=3,000/110=27.27A — refrigerator — i g =400/110=3.63A — TV — i TV =150/110=1.36A — lamp — i l =60/110=0.54A — 30 missing – 27.7=2.3A — R- Lamp and TV
38-
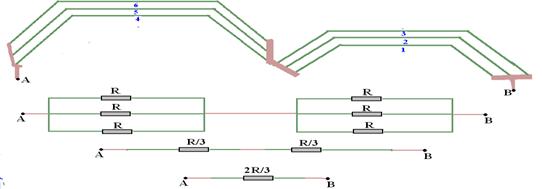
P=U 2 /R eq — P=U 2 /(2R/3) — P=3U 2 /2R
39- Total current i in the circuit breaker — P t =i t. U — (1,400 + 920)=i t .110 — i t =21.1A — for the circuit breaker not to trip, the minimum electric current must be 25 A — R- D
40- Lamp Q — P Q =U 2 /R — P R =U 2 /R — P S =(U/2) 2 /R=U 2 /4R — R- B
41 – Data — U = 12.4 V — i = 0.8 A — R 1 = 0.2 Ω — r = 0.3 Ω — equivalent resistance of the association — U = Req .i — 12.4 = Req 0.8 — Req =12.4/0.8 — Req = 15.5 Ω — the resistance values are in arithmetic progression (AP) —
a n = a 1 + (n – 1) r — R n = R 1 + (n – 1) r — R n = 0.2 + (n – 1) 0.3 — R n = 0.3 n – 0.1 — as the resistors are associated in series, the equivalent resistance is the sum of the resistances — sum of the first n terms of an AP — S n = (a 1 + a n ).n/2 — R eq = (R 1 + R n ).n/2 — 15.5={0.2 + (0.3n – 1).n}/2 — 31=0.3n 2 + 0.1n — 3n 2 + n – 310=0 — solving the second-degree equation — n= (-1 ±√3.721)/6 — disregarding the negative answer — n= (-1 + 61)/6 — n=10 — R- A
42- (01) Correct — the electrical power is given by: P = U 2 /R, where R is the electrical resistance — as the voltage is the same for both bulbs, the one with greater power has less resistance, that is, R A < R B — Ohm’s second law — R = ρL/S — in this expression, ρ is the resistivity of the material; S is the cross-sectional area of the filament and L is its length — if both are made of the same material and have the same diameter, the resistance will be directly proportional to the length — R A < R B and
L A < L B .
(02) Correct — the luminous intensity is directly proportional to the luminous power emitted — luminous power of A — P’ A = 30% of 100 = 0.3(100) = 30 W — luminous power of B P’ B = 30% of 40 = 0.3(40) = 12 W — P A ‘/P B ‘=30/12=2.5
(04) Correct — the resistivity of the filament increases with temperature — the brightness of a lamp is due to the heating of its filament to high temperatures — thus, when turned off, the lamps have lower resistivity, consequently, lower resistance.
(08) False — when they are connected in series, both are traversed by the same electric current — electrical power —
P d = R i 2 — as already concluded, R A < R B — then P A < P B — the luminous intensity of A is less than that of B .
(16) False — As already justified, R A < R B .
R- (01+ 02 + 04) = 07
43-


44- I. Correct — in every series association the intensity of the electric current is the same.
II. Calculation of the resistance, assumed constant, of each lamp — P 1 = U 2 /R 1 — 60=14,400/R 1 — R 1 =240Ω — P 2 = U 2 /R 2 —
100=14,400/R 2 — R 2 =144Ω — equivalent resistor — R eq =240 + 144 — R eq =384Ω — electric current in each resistor —

R eq =U/i — 384=120/i — i=120/384 — i=0.3 A — calculation of the power dissipated in each lamp — P 1 =R 1 .i 2 =240.0.9 — P 1 =216W — P 2 =R 2 .i 2 =144.0.9 — P 2 =129.6W — lamp 1 shines brighter, since P 1 >P 2 — correct
III. False — see previous justification
45- The wrong statement is C — see sequence below — R eq = 0.72 + 1.44 + 1.44=3.6Ω — R eq = U/i — 3.6=6/i — i=1.66 A

R-C
46- I. False – In a series connection, the electric current that runs through the bulbs is the same. Therefore, when a bulb burns out, the circuit opens.
II. False – In a series connection, the total ddp is divided between the two lamps. Therefore, they will have a ddp of 110V, not working as specified in the problem.
III. False – The total voltage is 220V. If we place two 110V bulbs in series, they will work correctly.
IV. True – As stated in statement II, each lamp will be subjected to a 110V ddp.
R-B
47- Data — R 1 = R and R 2 = 3R — equivalent resistance in series — R s = R 1 + R 2 = R + 3 R — R s = 4 R — where E is the force

electromotive force of the ideal battery, the power supplied by it in this association is — Ps=U 2 /R s =E 2 /R s — P s =E 2 /4R (I) — equivalent resistance in parallel — when one is three times the other, divide the larger by 4 — R p =3R/4 — power supplied — P p =U 2 /R p =E 2 /R p — P p =E 2 /(3R/4) — P p =4E 2 /3R (II) — dividing member by member (I) by (II) — Ps/P p =E 2 /4Rx3R/4E 2 —
Ps/P p =3/16
48- The three resistors are in parallel, therefore ddp is the same for all three, that is, U = 24 V — resistor R 3 — P 3 = U 2 /R 3 —
R 3 =24 2 /32 — R 3 =18Ω — calculation of R rq — 1/R eq =1/3 + 1/9 + 1/18 — R eq =2Ω — R- E
49- R eq =2,000/2 — R eq =1,000Ω — P=U 2 /R=100 2 /1,000 — P=10W — R- D
50- P=iU — i=55/36 A — when connected to the same fuse, the current doubles — I=2.(55/36) — I=3.05 A — to support this electric current, the lowest value of the fuse must be 5 A, that is, orange — R- C
51- Reversing the polarity of the battery only reverses the direction of the current without changing the other characteristics of the circuit — note in the expression P=U2 / R that the power is inversely proportional to the resistance of the lamp — thus, the lower the resistance of the filament, the greater the power and consequently the greater the brightness — R-C
52- The two resistors are in parallel — Req=100/3Ω — Req=U/i=E/i — 100/3=E/1 — E=100/3V — R- B
53-

54- R- C — see theory
55) – Calculation, using nominal values, of the current that must flow through each lamp — P=iU — 6=i.10 — i=0.6 A — in the parallel association, the total current of the fuse (currently circuit breaker) of 6 A,
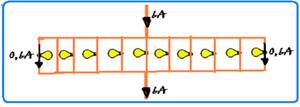
divides, passing 0.6 A through each lamp — n=6/0.6=10 lamps — R- C .
56- Note in the figure that, as the 12V battery is connected to points A and B, the 5kΩ resistors
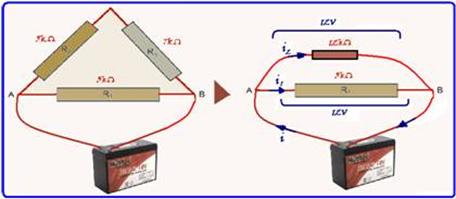
and 7kΩ are in series and replaced by a single 12kΩ resistor — now the 12kΩ and 3kΩ resistors are in parallel and subjected to the same ddp as the battery of U=12V — i 2 =U/R=12/12k — i 2 =1mA — i 1 =U/R=12/3k — i 1 =4mA — i=i 1 + i 2 =1 + 4=5mA — R- A
57- All must be connected in parallel, as they must be under the same ddp of U = 120V — calculation of each resistance — 3 lamps — P o = U 2 / R 1 — 300 = 14,400 / R 1 — R 1 = 14,400 / 300 — R 1 = 48Ω — sandwich plate — P o = U 2 / R 2 — 2,000 = 14,400 / R 2 — R 2 = 14,400 / 2,000 — R 2 = 7.2Ω — microwave oven — P o = U 2 / R 3 — 1,500 = 14,400 / R 3 — R 3 = 14,400 / 1,500 — R 2 = 9.6Ω —
calculation of the equivalent resistance of these three resistors that are connected in parallel —

1/R eq =1/48 + 1/7.2 + 1/9.6 —
1/R eq = (69.12 + 460.8 + 345.6)/3 317.76 — R eq ≈3.8Ω — R eq =U/i total — 3.8=120/i total — i total =31.6 A — any value less than 31.6 A turns off the circuit breaker — R- E
58- See in the figure how the circuit should be assembled in a series association — in this association, so that the lamps
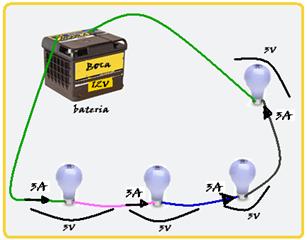
work fully and efficiently, they must be connected within specifications (3V-9W) — so, each lamp must be carried by a current of P=iU — 9=3.i — i=3 A — the total voltage U=12V must be equal to the sum of the voltages of each lamp, so you will have n=12V/3V=4 lamps — resistance of each lamp — R=U/i=3/3=1Ω — equivalent resistance — R eq =4×1=4Ω — total power of the circuit — P t =U t .i=12.3 — P t =36W — R- A .
59- As these resistors have different intensities and are traversed by the same electric current, they are

associated in series — equivalent resistance — R eq =4 + 2=6Ω — R eq =U/i — 6 = 12/i — i=2 A — R- D .
