Segunda lei de Ohm (Resistividade) – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Segunda lei de Ohm (Resistividade)
01- Como são de mesmo material, possuem a mesma resistividade elétrica — R- B
02- A resistência R é inversamente proporcional à espessura (S) — maior espessura, menor R, maior corrente i — brilha mais — R- E
03- Mesmo fio — mesma resistividade ρ — mesma S — L cai pela metade — R é diretamente proporcional a L — R também cai pela metade — R- B
04- R é inversamente proporcional à área de seção reta transversal S — S=πr2 — a nova área ficará 4 vezes maior, pois R está ao quadrado, e a resistência R ficará 4 vezes menor — R é diretamente proporcional ao comprimento L — se L é reduzido à metade, R também será reduzido à metade — R’=R/4.2=R/8 — R- D
05- Reduzindo o comprimento à metade — R fica 2 vezes menor — reduzindo o diâmetro (r/2) à metade — R fica 4 vezes maior — R’=(1/2 x 4)R — R’=2R — R- C
06- (01) Quando a temperatura da maioria dos metais aumenta, há um aumento no movimento vibratório de seus átomos e moléculas, que dificultam a passagem da corrente elétrica diminuindo-a, o que provoca um aumentando de sua resistência elétrica. Como a resistividade é diretamente proporcional à intensidade da corrente elétrica, ela também aumenta — Falsa.
(02) Correta — resistor ôhmico, R constante — U é diretamente proporcional a i.
(04) Falsa — Se a área S dobra, a resistência R cai pela metade.
(08) Falsa — W=Po.Δt=i.U.Δt — i é a intensidade da corrente que independe de seu sentido e, observe na fórmula, depende da tensão U.
(16) Falsa — corrente elétrica é um movimento ordenado de elétrons.
(32) Verdadeira — veja teoria.
R- (02 + 32)=34
07- R1=R — R é inversamente proporcional à S — R2=R/2 — P1=U2/R — P2=U2/(R/2) — P2=2U2/R — P1/P2=U2/R x R/2U2 — P1/P2=1/2 — R- B
08- Sendo o mesmo material, a resistividade ρ é a mesma — quando ele é estirado, como mantém o mesmo volume, o comprimento

passa a 2L e a nova espessura a S1 — V=S.L — V=S1.L1 — S.L=S1.2L — S1=S/2 — R=ρ.L/S (I) — R1=ρ.L1/S1 — R1=ρ.2L/S/2 — R1=4ρ.L/S (II) — comparando (II) com (I) — R1=4R — R- A
09- Maciço — Rmaciço=ρ.L/πR2 — oco — Smaior=π(R)2 — Smenor=π( r )2 — S=π.R2– π.r2 — S=π( R2 – r2) — a expressão da resistência fica — Roco=ρ.L/π(R2 – r2) — Rmaciço/Roco= ρ.L/πR2 x π(R2 – r2)/ρL — Rmaciço/Roco=(R2 – r2)/R2= 1 – r2/R2 — R- B
10- P2=4P1 — m2=4m1 — mesmo material, mesma densidade — d=m1/V1 — d=m2/V2 — m1/V1=4m1/V2 — V2=4V1 — V1=S1.L1=S1.25 — V2=S2.L2=S2.75 — V2=4V1 — 75S2=4.25.S1 — S2=4S1/3 — R1=ρL1/S1 —
4= ρ.25/S1 — ρ=4.S1/25 — R2= ρ.L2/S2=4.S1/25.75/(4S1)/3 — R2=75.3/25 — R2=9Ω
11- I. Entre A e C — maior resistência — menor corrente — menor potência — aquece menos — correta
II. Falsa — veja I.
III. Falsa — quente é entre B e C (menor R, maior potência, aquece mais) e não entre A e C.
R- C
12- RA=ρA.L/π(rA)2=10-6.L/π(0,25)2 — RA=16.10-6L/π — RB=ρB.L/π(rB)2=1,2.10-6.L/π.(0,25)2 — RB=19,2.10-6L/π — RC=ρC.L/π(rC)2=1,5.10-6.L/π.(0,2)2 — RC=37,5.10-6L/π — R- E
13- a) L=3.(4.10-10)=12.10-10m — R=ρ.L/A — R=ρ.L/π.(r)2 = 1,6.10-8.12.10-10/3,2.(2.10-10)2 — R=19,2.10-18/12,8.10-20 — R=1,5.102Ω
b)R=U/i=10-1/8.10-6 — R=0,12.105 — R=1,2.104Ω
14- A resistência por unidade de comprimento=ρ/S — R=ρL/S=5.10-5.6.10-2=30.10-7 — R=3.10-6Ω — R=Ui — 3.10-6=U/103 — U=3.10-3 A — R- C
15- a) R=ρL/S=5,6.10-8.31,4.10-2/π(4/2.10-5)2 — R=175,84.10-10/3,14.4.10-10=175,84.10-10/12,56.10-10 — R=14Ω
b) Po=U2/R — 100=(120)2/R — R=14.400/100 — R=144Ω (observe que, com a lâmpada acesa a temperatura aumenta, aumentando assim o movimento vibratório dos átomos e moléculas do tungstênio.o que dificulta a passagem da corrente elétrica, aumentando portanto a resistência).
16- a) R=ρL/S=1,6.10-8.10/4.10-6=1,6.10-7/4.10-6 — R=0,4.10-1 — R=0,04Ω
b) Corrente que chega à residência — Po=i.U — 3.300=i.110 — i=30 A — da caixa de relógio até a residência existem dois fios — R=2.0,04=8.10-2Ω — Po=R.i2=8.10-2.900 — Po=72W
17- A ponte de Wheatstone é um dispositivo que permite determinar o valor de resistência elétrica desconhecida — Rx=ρL/S — Rx varia de 10Ω até 12Ω — Rx=10Ω — 10=ρ1L/S (I) — Rx=12Ω — 12= ρ2L/S (II) — subtraindo (II) de (I) — 2=( ρ2 – ρ1).L/S — 2=Δρ.L/S — 2=Δρ.10/0,1.10-6 — Δρ=2.10-8Ωm — pelo gráfico — regra de três — Δρ (2.10-8Ωm) – Δt oC — (ρ – ρo) (0,8.10-8Ωm) – 89oC — 0,8.10-8.Δt=160.10-8 — Δt=200oC
18- Rantes=R(6R/¨) — comprimento 6 vezes menor Rdepois=5R/6 — Poantes=U2/R — Podepois=U2/5R/6=6U2/5R — Poantes/Podepois=U2/R x5R/6U2 — Poantes/Podepois=5/6 — R- E
19-RA=2RB — LA=2LB — AS=SB/4 — ρ=R.S/L — ρA=RA.SA/LA — ρA=2RB.(SB/4)/2LB — ρA/ρB= 2RB.(SB/4)/2LB x LB/RB.SB — ρA/ρB=RBSB/2LB x LB/RBSB — ρA/ρB=1/2 — R- B
20- Para que a corrente seja a mesma em cada linha, as duas devem ter a mesma resistência elétrica — R=ρL/S —
S=π( r )2 =π.(d/2 )2 — S=πd2/4 — R1=ρ(72 + 72)/π.(d12/4)=4.144/πd12 — R2=ρ100/π(d22/4)=4.100/ πd22 —
R1=R2 — 4.144/πd12=4.100/ πd22 — (d1/d2)2=144/100 — d1/d2=12/10 — d1/d2=1,2
21- R1=R — R2=0,8R — P1=U2/R — P2=U2/0,8R — P1/P2=U2/R x 0,8R/U2 — P2=P1/0,8 — P2=1,25P1 — P2=125%P1 — R- B
22- W=Po.Δt=(U2/R).Δt — maior potência, menor resistência, consome mais energia — menor resistência – substituindo os valores de cada alternativa na equação R=ρ.L/S, chega-se à resposta — R- C
23- a) R=ρL/S=1,7.10-8.1/3,5.10-6 — R=0,486.10-2 — R=4,86.10-3Ωm
b) R=ρL/S — 2.10-2=1,7.10-8.10/S — S=1,7.10-7/2.10-2=85.10-7m2 — S=8,5mm2 — S=π.r2 — 8,5=3,14.r2 — r=√2,71 — r=1,6mm — d=2.r=2.1,6 — d=3,2mm — calibre 8
24- I- Correta — Po=R.i2 — quanto maior i, maior Po
II- Correta — R=ρL/S — quanto maior ρ, maior R e menor i
III- Falsa — é a razão U/i que é constante e não o produto U.i
IV- Correta — Falsa — depende do tipo de associação (série, paralelo ou mista)
R- D
25- (01) Errada. Resistor é um dispositivo elétrico para CONTROLAR a intensidade da corrente elétrica.
(02) Errada. A resistividade de um material só depende dele próprio e de sua temperatura.
(04) Correta. Quando se acrescentam novas lâmpadas em série, aumenta-se a resistência equivalente do conjunto, diminuindo a corrente. Como P = Ri2, reduz-se também a potência dissipada em cada uma delas, diminuindo as intensidades luminosas.
(08) Correta. De acordo com a Segunda Lei de Ohm, a resistência depende: do material de que é feito o condutor, das dimensões do condutor e da temperatura.
R- (04 + 08) = 12
26- Sendo ρ a resistividade do material, L o comprimento do condutor e A a área de sua secção transversal, a segundo lei da Ohm nos dá que a resistência (R) desse condutor é — R=ρL/A — dobrando o comprimento e reduzindo à metade a área de sua secção transversal, a nova resistência passa a ser — R’=(ρ2L)/A/2=4(ρL/A) — R’=4R — R- B
27- a) Dados — A = 1,6.10-2 mm2 = 1,6.10-8 m2 — L = 2 m — do gráfico — quando a temperatura é T = 3.000 °C, a resistividade é ρ = 8.10-7 Ω.m — segunda lei de Ohm — R= ρL/S=8.10-7.2/1,6.10-8 — R=100Ω
b) Dados — λ = 12.10-6 °C-1 — T’ = 20 °C — T = 3.000 °C — 3.000 °C, o volume inicial é — Vo = S.L = 1,6.10-8. 2 —
Vo= 3,2.10-8 m3 — variação volumétrica — ΔV = Vo.λ.(T’ – T) = 3,2.10-8.12.10-6 (20 – 3.000) — ΔV= – 1,1.10-9 m3=-1,1mm3
— o sinal (–) indica que o material sofreu contração.
28- Dados — D = 2 cm = 2.10-2 m — L = 2.103 m — i = 103 A; — Δt = 1 h = 3,6.103 s.
A resistência da linha é dada pela 2ª lei de Ohm — R=ρL/S — área da secção transversal — S= πr2 =π(D/2)2 — S=πD2/4 —
R=ρL/S=4ρL/(πD2/4)=4(1,57.10-8).(2.103)/3,14.(2.10-2)2 — R=0,1Ω — Po=R.i2 — Po=ΔW/Δt — ΔW=Po.Δt —
ΔW=R.i2.Δt — ΔW=0,1.(103)2.3,6.103 — ΔW=3,6.108J — R- A
R- A
29- Dados — c = 4.200 J — ΔT = (100 – 28) = 72 °C — Q = ΔW = 3,6.108 J — equação do calor sensível — Q = m c ΔT — m = Q/cΔt=3,6.108/4,2.103.72 — m=1,2.103 kg — R- B
30- Baseado nas figuras:
(1) Mantendo-se a secção transversal constante e dobrando-se o comprimento (ℓ) do fi o, a resistência (R) dobra — então, a proporcionalidade entre ℓ e R é direta.
(2) Mantendo-se o comprimento constante e dobrando-se a área da secção transversal (A), a resistência (R) fica dividida por dois — então, a proporcionalidade entre A e R é inversa.
(3) Mantendo-se a resistência constante e dobrando-se o comprimento (ℓ) do fio, a área da secção transversal (A)
dobra. Assim, a proporcionalidade entre ℓ e A é direta.
R- C
31- As figuras 1 e 2 ilustram a situação descrita.
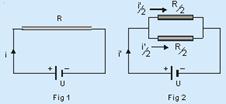
Considere que na Fig 1 a resistência elétrica do fio é R e a corrente é i — sendo U a ddp fornecida pela bateria, aplicando a 1ª lei de Ohm — R=U/i — i=U/R — de acordo com a 2ª lei de Ohm, a resistência elétrica é diretamente proporcional ao comprimento Então, ao se cortar o fio ao meio, a resistência elétrica de cada pedaço é metade da resistência do fio inteiro —
R1=R2=R/2 — colocando-se os dois pedaços em paralelo como na Fig 2, a resistência do circuito é — R’=(R/2)/2 — R’=R/4 — corrente i’ no circuito — U’=U/R’=U/(R/4) — U’=4U/R — U’=4i — correntes nos pedaços — i1=i2=i’/2=4i/2 — i1=i2=2i — R- A
32-

