Resolução comentada dos exercícios de vestibulares sobre Circuitos com geradores

Resolução comentada dos exercícios de vestibulares sobre

Circuitos com geradores

 

01– Os dois resistores estão em série  —  R_eq=(R + 20)  —  R_eq=U/i  —  (R + 20)=6/0,1  —  R + 20=60  —  R=40Ω  —  R- C  

02- a) Com a chave C fechada, L₂ e L₃ estão em paralelo  —  R’=30/2=15Ω  —  R’fica em série com a resistência de R₁=30Ω  —  R_eq=15 + 30  —  R_eq=45Ω  —  R_eq=U/i  —  45=18/i  — 

i=0,4A  —  chave fechada  —  corrente que passa por i_L1==0,4A e por L₂  —  i_L2=0,4/2  —  i_L2=0,2A

b) Chave aberta  —  só passa corrente por L₁ e por L₂, que estão em série  —  R_eq=30 + 30  —  R_eq=60Ω  —  R_eq=U/i  —  60=18/i_L1=  —  i_L1=18/60  —  i_L1=0,3A  —  chave aberta  —  por L₁  passa 0,3A   —  chave fechada  —  por L₁ passa 0,4A —  abrindo-se a chave, porL₁ passa menor corrente e ela brilha menos.

03- a) Chave C aberta   

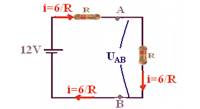
 R_eq=2R  —  R_eq=U/i  —  2R =12/i  —  i=6/R   —  U_AB=R.i  —  U_AB=(6/R).R  —  U_AB=6V

b) Chave C fechada  —  observe a sequência abaixo

R_eq=U/i  —  3R/2=12/i’  —  i’=24/3R  —  i’=8/R  —  U_AB=R.i  —  U_AB=R/2.8/R  — U_AB=4V

04-

Quando R₃=0

 os pontos A e B estão em curto circuito e U_AB=0

Quando R₃=6Ω  —  observe as seqüências abaixo

R_eq=U/i  —  4=1,2/i  —  i=0,3A  —  U_AB=R.i=2.0,3  —  U_AB=0,6V

05- O “fio terra” indica que o potencial no ponto B é nulo (V_B=0­)  —  R_eq=1 + 2 + 4  —  R_eq=7Ω  —  R_eq=U/i  —  7=14/i  —  i=2 A  —  U_AB=R_AB.i  —  V_A – V_B=4.2  —  V_A – 0=8  —

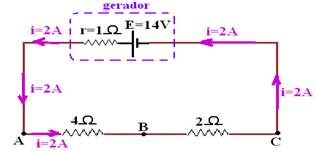
  V_A=8V  —  U_BC=V_B – V_C=R_BC.i  —  0 – V_C=2.2  —  V_C= – 4V  —  R- D  —  Obs: Se a polaridade do gerador fosse invertida, o sentido da corrente também seria invertido e os valores seriam V_A= – 8V e V_C=2V

06- A ligação terra torna o potencial do ponto A nulo  —  (V_A=0)  —  cálculo de i  —  R_eq=U/i  —  12=12/i  —  i=1A  —  chamando o terminal negativo do gerador de C e o positivo de B  —

  U_AC=V_A – V_C=R.i  —  0 – V_C=9.1  —  V_C= – 9V  —  R- C  —  Obs.  —  observe que  —  U_BA=V_B –V_A=R.i  —  V_B – 0=3.1  —  V_B=3V  —  observe ainda que V_B – V_A=3 – (-9)=12V

07- a) No fio neutro o potencial é nulo  —    diferença de potencial (tensão) entre os pontos A e P (quatro lâmpadas de cima) é V_A – V_P=110 – 0=110V, e nas duas lâmpadas de baixo (entre P e B) é V_P – V_B=0 – (-110)=110V  —  R- 110V

b) Se o fio quebrar em P  —  curto circuito  —  refazendo o circuito (figuras abaixo)  —  as 4 lâmpadas de cima estão em paralelo (r/4) e as duas de baixo também estão em paralelo (r/2)  –

—  U_AB=V_A – V_B=110 – (- 110)  —  U_AB=220V  —  R_eq=3r/4  —  R_eq=U/i  —  3r/4=220/i  —  i=4.220/3r  —  i=880/3r  —  tensão (U_PB) na parte de baixo (duas lâmpadas em paralelo R_rq=r/2) vale  —  R_eq=U/i  —  r/2=U_PB/880/3r  —  U_PB=r/2×880/3r  —  U_PB=147V

08- R_eq=0,1 + 1,9 + (18/3) + 2  —  R_eq=10Ω  —  R_eq=U/i  —  10=12/i  —  i=1,2 A  —  veja nas seqüências abaixo que a corrente que flui pelo resistor de 9Ω é i’’=0,8 A  —P=i.U  — 

P=0,8.7,2  —  P=5,76W

09- a) chave fechada  —  R_eq=r + 3,5  —  i=3 A  —  U= ε=12V  —  R_eq=U/i  —  r + 3,5=12/3  — r=0,5Ω

b) equação do gerador (bateria)  —  U=E – r.i  —  U=12 – 0,5.3  —  U=10,5V

c) P_útil=U.i=10,5.3  —  P_útil=31,5W  —  η=U/ ε=10,5/12  —  η=0,875  —  η=87,5%

d) potência liberada (dissipada) pelo resistor  —  P_d=R.i²=3,5.(3)²  —  P_d=31,5W  —  energia dissipada na água em Δt=10min=10.60  — Δ t=600s  —  W=P_d.Δt=31,5.600  — W=18.900J

e) como 1J=0,24cal  —  W=18.900.x0,24  —  W=Q=4.356cal  —  Q=m.c.Δθ  —  4.356=240.1. Δθ  —  Δθ=18,15^oC

10- R_eq=U/i  —  4/3= ε/9  —  ε=12V

11- Cálculo da resistência de cada lâmpada  —  P=U²/R  —  0,5=(1)²/R  —  R=2Ω  —  Chave aberta  —  R_eq=U/i  —  6 + 2r=(1,5 + 1,5)/0,3  —  2r=4  —  r=2Ω  —  chave fechada  — 

R_eq=U/i  —  6 + 2=3/i  —  i=3/8=0,375  —  i=375mA  —  R- B

12- A ddp U que o gerador fornece ao circuito esterno (resistência R=12Ω) vale  —  R=U/i  —  12=U/2  —  U=24V  —  η=80%=0,8  —  η=U/E  —  0,8=24/E  —  E=24/0.8  —  E=30V  — 

Equação do gerador  —  U=E – r.i  —  24=30 – r.2  —  r=3,0Ω  —  R= E

13- Chave aberta  —  como as lâmpadas são idênticas, a tensão V em cada lâmpada é a mesma  —  chave fechada  —  como a tensão em L₂ continua a mesma, a tensão em L₁também será a mesma e as duas lâmpadas continuarão com o mesmo brilho  —  R- E

14- Cálculo da resistência da lâmpada  —  P=U²/R  —  0,6=9/R  —  R=15Ω  —  corrente na lâmpada  —  R=U/i  —  15=2,5/i  —  i=0,1666A  —  equação do gerador  —  U=E_eq – r_eq.i  —

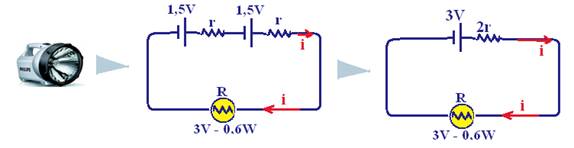
2,5=(1,5 + 1,5) – 2r.0,1666  —  r=0,5/0,333  —  r=1,5Ω  —  R- A

15- As três pilhas em série fornecem uma fem total de E=4,5V  —  como todos os elementos estão em série a tensão total fornecida (E=4,5V0 é igual  à soma das tensões parciais  — 

E= U_M +U_R  —  4,5=4 + U_R  —  0,5=R.i  —  0,5=1.i  —  i=0,5 A  —  potência do motor  —  P=U.i=4.0,5  —  P=2,0W  —–  R- D

16- A resistência equivalente é a de 6 salsichas em paralelo  —  Req=440.000/6Ω  —  Potência empregada pelo sistema  —  P=U2/Req(110)2/(440.000/6)  —  P=0,165W  — 

energia em 20s  —  W=P.Δt=0,165.20  —  W=3,3J  —  R- C

17- a) A potência P_o é dada por  —   P_o = U²/R_o  P —   _o = (120)²/12  —   P_o = 1200 W

b) De acordo com o enunciado P₁ = 2 . P₂  —  U²/R₁=2.U²/R₂  —  R₂=2R₁  —  R₁ + R₂=12  —  R₁ + 2R₁=12  —  R₁=4Ω e R₂=8Ω

c) A potência P é dada por  —  P=P₁ + P₂=U²/R₁ + U²/R₂  —  P_o=U²/R_o  —  P/P_o=(U²/R₁ + U²/R₂)/U²/R_o  —  P/P_o=(1/4 + 1/8)/1/12  —  P/P_o=4,5

18- a) Como a tensão entre X e Y é U_XY=16V, a corrente no resistor de 8Ω será  —  R=U_XY/i   —  8=16/i  —  i=2 A  —  a tensão entre os pontos M e N, onde i=2 A vale U_MN=R’.i=(8 + 7).2

—  U_MN=30V  —  no resistor de 30Ω a tensão também é U_MN=30V  —  R=U_MN/i’  —  30=30/i’  —  i’=1 A  —  i_total=2 + 1  —  i_total=3 A  —   R_eq=15 paralelo com 30(10Ω) + 30  —  R_eq=40Ω  —  R_eq=U/i  —  40=E/3  —  E=120V

b) E=240V  —  R_eq=40Ω  —  R_eq=U/i_t  —  40=240/i_t  —  i_t=6 A  —  como uma resistência é o dobro da outra, as correntes nos ramos de 30Ω e (7Ω e 8Ω) serão o dobro uma da outra de

 maneira que sua soma seja 6 A  —  i=4 A e i’= 2 A  —  U_XY=R.i=8.4  —  U_XY=32V

19- Cálculo da tensão U em L₃ onde i₃=500mA=0,5 A  —  P₃=i₃.U  —  2=0,5.U  —  U=4V  —  esta tensão (U=4V) é a mesma para as três lâmpadas (estão em paralelo)  —  L₂  —  P₂=i₂.U  —  2=i₂.4  —  i₂=0,5 A  —  L₁  —  P₁=i₁.U  —  1=i₁.4  —  i₁=0,25 A  —  i=i₁ + i₂ + i₃=0,5 + 0,5 + 0,25  —  i=1,25 A  —  equação do gerador  —  U=E – r.i  —  4=E – 0,2.1,25  —  E=4,25V  —  R- E

20- Do enunciado  —  U=E/3  —  E=3U  —  U=R.i  —  U=6i  —  E=3.U  —  E=3.6i=18i  —  equação do gerador  —  U=E – r.i  —   6i= 18i – r.i  —  r=12Ω  —  R- E

21- R_eq=3R paralelo com 3R  —  R_eq=1,5R  —  R_eq=U/i  —  1,5R= ε/i  —  i= ε/1,5R  —  em cada ramo de resistências iguais (3R) a corrente i= ε/1,5R se divide pela metade  —   i₁= ε/3R e

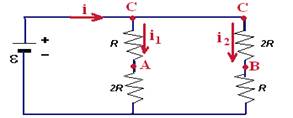
i₂=ε/3R  — V_C – V_A=R.i₁  —  V_C – V_A=R. ε/3R  —  V_C – V_A= ε/3 ( I )  —  V_C – V_B=2R.i₂  —  V_C – V_B=2R. ε/3R  —  V_C – V_B= 2ε/3 ( II )  —  subtraindo (II) de (I)  — 

V_C – V_B – (V_C – V_A)= 2ε/3 – ε/3  —  V_A – V_B=ε/3

22- a) Falsa  —  L₁ é percorrida por corrente maior que a de L₂ e de L₃ e brilha coma maior intensidade  (i₁=i₂ + i₃)

b) Correta  —  sendo as lâmpadas idênticas  —   i₂=i₃=i  —  i₁=i₂ + i₃  —  i₁=i + i  —  i₁=2i e i₂=i

c) Falsa  —  são iguais

d) Falsa  —  apenas L₂ e L₃ estão submetidas ao mesmo potencial

e) Falsa  —  a potência dissipada por L₁ é maior que a dissipada por L₂, pois L₁ é percorrida por maior corrente

R- B

23- 01. Falsa  —  lâmpadas idênticas em série  —  percorridas pela mesma corrente  —  brilham por igual

02. Correta  —  veja 01

04. Falsa  —  brilham por igual  —  mesma ddp e mesma corrente

08. Correta  —  é percorrida por maior corrente, pois tem menor resistência

16. Falsa  —  a lâmpada B apaga, entra em curto circuito

Corretas  —  02 e 08

24- a) Colocando os valores e construindo o gráfico

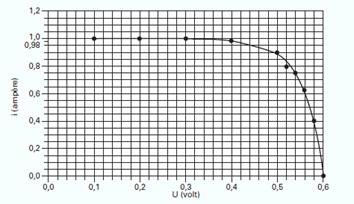
25-

 

26- Observe que, como a corrente total é 1,0A e se, por R_A passa 0,5 A pelo resistor de 0,5Ω passará também 0,5 A  —  por R_B

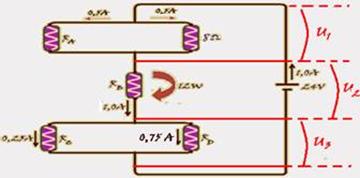
passará 1,0 A e por R_D=0,75ª  —  como R_A e 8Ω estão em paralelo eles estão submetidos à mesma diferença de potencial U₁, tal que  —  R=U₁/i  —  8=U₁/0,5  —  U₁=4V  —  em B  —  P_B=i_B.U₂  —  12=1.U₂  —  U₂=12V  —  U₁ + U₂ + U₃ = U_total=24V  — 

4 + 12 + U₃=24  —  U₃=8V  —  a potência elétrica dissipada no resistor R_D vale  —  P_D=i_D.U₃=0,75.8  —  P_D=6W  —  R- C

27- Modo A  —  chave C  ligada no ponto A  —  como as lâmpadas estão ligadas em série, cada uma delas ficará sob ddp de 60V , dissipando uma potência de 60W —  cálculo da resistência elétrica R de cada uma  —  P=U²/R  —  60=60²/R  —  R=60Ω  —

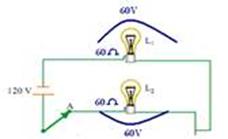
R_eq=60 + 60=120Ω  —  potência total dissipada  —  P_total=U²/R_eq=120²/120  —  P_total=120W  —  energia elétrica consumida em 4h  —  P_total=W/∆t  —  120=W/4  —  W=480Wh=0,48kWh

Modo B  —  chave C ligada ao ponto B  —  L₂ fica apagada (não passa corrente por ela)  —  para que a lâmpada L₁  de

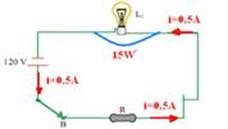
resistência R_L=60Ω dissipe uma potência de 15W, a corrente através dela deve ser  —  P_L2=R_l.i²  —  15=60.i²  —  i=√(0,25)  —

i=0,5 A (é a mesma corrente que passa por R, R e 60Ω estão em série)  —  R_eq=(R + 60)  —  U=120V  —  R_eq=U/i  —  R + 60 = 120/0,5  —  R + 60=240  —  R=180Ω

28-

  a) Aquecedor  —  P_aq=990W  —  ∆t=3h  —  P_aq=W_aq/∆t_aq  —  990=W_aq/3  —  W_aq=2.970 Wh  —  ferro  —  P_fe=980W  —  ∆t=3h  —  P_fe=W_fe/∆t_fe  —  980=W_fe/3  —  W_fe=2.940 Wh  —  2 lâmpadas  —  P_L=2.60=120W  — ∆t=3h  —  P_L=W_L/∆t_L  —  120=W_L/3  —  W_L=360 Wh  —  chuveiro  —  P_ch=4.400W  —  ∆t=12min=12/60=0,2h  —  P_ch=W_ch/∆t_ch  —  4.400=W_ch/0,2  —  W_ch=880 Wh   —  energia total  —  W_total=2.970 + 2.940 + 360 + 880  —  W_total=7.150Wh  —  W_total=7,15kWh.

b) Cálculo da intensidade de corrente elétrica em cada aparelho  —  aquecedor  —  P_aq=i_aq.U_aq  —  990=i_aq.110  —  i_aq=9 A  —  ferro  —  P_fe=i_fe.U_fe  —  980=i_fe.110  —  i_fe=98/11 A  —  cada lâmpada  —  P_L=i_L.U_L  —  60=i_L.110  —  i_L=6/11 A  —  chuveiro  —  P_ch=i_ch.U_ch  —  4.400=i_ch.220  —  i_ch=20,0 A  —  observe atentamente o esquema da figura e o circuito abaixo onde foi tirado o fio terra, já que por

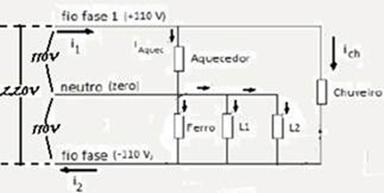
ele não passa corrente elétrica  — a corrente i₁ no fio fase 1 se divide nas correntes que passam pelo aquecedor e pelo chuveiro, ou seja, i₁=i_aq + i_ch= 9 + 20=29,0 A  — a corrente i₂ no fio fase 2 recebe as correntes que passam pelo ferro,  pelas duas lâmpadas e pelo chuveiro, ou seja, i₂= 6/11 + 6/11 + 98/11 + 20  —  i₂=29,98  —  i₂≈30 A.

c) Observe nas figuras abaixo que no ponto P chegam as correntes do fio neutro i_n e do aquecedor i_aq e e sai a corrente i’ que corresponde

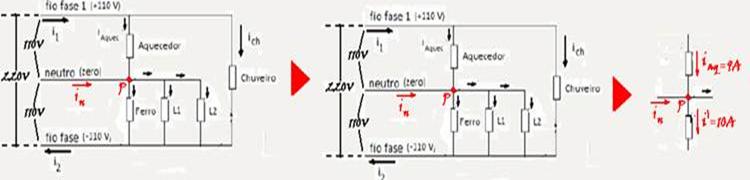
às somas das correntes que passam pelo ferro e pelas lâmpadas  —  i_n+i_aq = i’  —  i’=98/11 + 6/11 + 6/11=10 A  —  i_n + 9=10  —  i_n=1 A.

 

Voltar para os exercícios