Primeira lei de Ohm – Resolução EN
OHM’S FIRST LAW – RESOLUTION
Commented resolution of entrance exam exercises on
Resistors – Ohm’s First Law – Electrical Power of a Resistor
01 – RA – see theory
02- For i=2 A — U=5.i 2 =5.2 2 =5.4 — U=20V — R=U/i=20/2 — R=5 Ω — R- A
03 – In every electrical circuit there must be a generator (battery), electrical wires conducting the electrical current and a conductor (lamp) — R- A .
04- R=U/i — 1,500=220/i — i=220/1,500 — i=0.1466 A — i=146.6mA — R- D
05- a) Since the relationship between voltage (U) and current (i) is constant, the resistor is ohmic. Applying Ohm’s law — when t=10s — U=0.5V and i=1.0A — R=U/i=0.5/1.0 — R=0.5Ω
b) The electrical power in the resistor is defined by the product Ui The area represents the dissipated energy.
06- R=U/i — 10 3 =220/i — i=220/10 3 — i=0.220 — R- D
07- U=10,000V, i=300mA=0.3a — calculation of the total resistance so that the person does not die — R=U/i=10,000/0.3 — R=3.33.10 5 Ω — being the resistance of the person’s body R p =2,000Ω, the electrical resistance of the air must complete this value — R=R p + R air —
3.33.10 5 =2,000 + R air — R air =3.31.10 5 Ω
08- Each wire is traversed by an electric current of i=0.75/150 — i=0.005 A and subjected to a ddp of U=220V — R=U/i=220/0.005 — R=44,000Ω=44kΩ
09- (01) False – only conductor III is ohmic
(02) True
(04) False – see calculations below
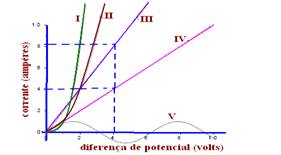
R III =U/i=4/8=0.5Ω — R IV =U/i=4/4=1Ω
(08) False – conductor V is not ohmic
(16) False – above 1V, the resistance of I is the smallest of all ohmic resistances
R- sum – (02)
10- Since R is constant, the ohmic resistor — either b or e — R=U/i — 2=10/5 — R- E
11- Since the resistor is ohmic, the ddp U is directly proportional to the electric current i — rule of three — 20V – 4 A – xV – 3 A — x=60/4 — i=15V
12- a) P=iU — 60=i.120 — i=0.5 A
b) R=U/i=120/0.5 — R=240Ω
13- Since U is constant — P o = U 2 /R — P o and R are inversely proportional — the 25W one has less resistance, as it has greater power.
14- When we close the tap a little, we are reducing the water flow and, consequently, reducing the mass of water that needs to be heated — R- C
15- P SC =P SP — U SC 2 /R SC = U P 2 /R P — U SC =2U P — (2U P ) 2 / R SC = U P 2 / R P — 4 U P 2 / R S = U P 2 /R P — R P =R SC /4 — R- C
16- Warm water – medium power – medium resistance — R- A
17- As P o = U 2 /R and U being constant, P o is inversely related to R — greater resistance (20.0Ω) – lower power – greater savings
18- R=U/i — 3=9/i — i=3.0A — P o =iU=3.9 — P o =27.0V — R- C
19- As the power is the same, the electric current will decrease and the shower circuit wiring can be thinner, providing savings — R- D
20- P o =U 2 /R — R=U 2 /P — substituting each alternative — R- C
21- It must be 4 times smaller — see theory — R= 8/4=2Ω — R- D
22- (01) Correct – lower power (less hot, lukewarm water), higher resistance
(02) Smallest R – largest i — R=U/i — 3=120/i — i= 40 A — correct
(04) P o =Ri 2 =8.15 2 =8.225=1.800W — correct
(08) Correct – see theory
(16) R=U/i — 3=120/i — i=40 A — false
R- (01 + 02 + 04 + 08) = 15
23- Ohmic resistor — same resistance — R=20Ω — R=U/i — 20=100/i — i=100/20=5 A — Po==iU=5.100=500W — R- E
24- 1 kW/m 2 = 1000 W/10000 cm 2 = 10 W/100 cm 2 — the cell receives 10 W. Since the efficiency is 12% this means that 1.2 W of solar energy are converted into electrical energy.
P o = Ui — 1.2 = 1.6.i — i = 1.2/1.6 = 0.75 — i=0.75A
25- R- C — see theory
26- Same power – same consumption – current i drops by half – see theory – R- B
27- a) being the same device — the resistance R is the same — P 220 =(U 220 ) 2 /R=220 2 /R — P 110 =(U 110 ) 2 /R=1100 2 /R — Z 1 =P 220 /P 110 — Z 1 =4
b) the dissipated energies are equal – W = P. Δt — W 110 = W 220 — P 110 . Δt 110 = P 220 . Δt 220 — Δt 110 = (P 220 / P 110 ). Δt 220 — note in the graph that the duration of a 220V cycle is 0.2s — Δt 110 = 4.0.2 — Δt 110 = 0.8s — but the duration of a continuous 110V cycle is 0.2 + Δt — 0.8 = 0.2 + Δt — Δt = 0.6s
c) the average current can be the constant current that provides the same average power — P m =RI m 2 — P m220 =P m110 — in the 0.8s cycle the dissipated energy is the same in both cases — R.(Im220)2= R.(Im110)2 — Z 2 =I m220 /I m110 =1 —
Z 2 = 1
28- Since the showers, operating with equal flow rates at the voltages indicated by the manufacturers, heat the water equally, the powers dissipated by R 1 and R 2 (with the showers operating according to the manufacturer’s specifications) are equal, that is, 110 2 /R 1 = 220 2 /R 2 . Consequently, we have R 2 = 4R 1 and, therefore, P 2 = (110V) 2 /R 2 = (110V) 2 /(4R 1 ), that is, P 1 /P 2 = 4. Since P 2 is smaller than P 1 , we see that changing the resistance had the desired effect, since with the resistance R 2 operating at 110V the power dissipated is four times smaller, heating the water less.
29- R is the same — P o =U 2 /R — 1200=(120) 2 /R — R=12Ω — P o1 =U 1 2 /R=(96) 2 /12 — P o1 =768W — R- B
30- P o =U 2 /R=(110) 2 /70 — P o =173W — R- D
31 – a) P o =U 2 /R=(120) 2 /12 — P o =1,200W
b) P 1 =2P 2 — U 2 /R 1 =2U 2 /R 2 — R 2 =2R 1 — R 1 + R 2 =12 — R 1 + 2R 1 =12 — R 1 =4.0Ω — R 2 =8.0Ω
32 – a) i=Q/Δt — 300,000=Q/0.5 — Q=150,000C — f=Q/Q total =150,000/600.00 — f=1/4
b) P o =Ui=5.10 6 .3.10 5 — P o =15.10 11 W — W=P o .Δt=15.10 11 .0.5 — W=7.5.10 11 J — 1kWh – 3.6.10 6 J — x kWh – 7.5.10 11 J — x=7.5.10 11 /3.6.10 6 — W=2.1.10 5 kWh
33- a) No — this relationship presents the definition of electrical resistance.
b) Yes — this relationship allows you to determine the electrical resistance of any resistor , whether it is ohmic or not.
c) Yes — the resistance R 1 = U/i is constant and equal to 2.2Ω.
34- Data — U = 600 V — R 1 = 2 kΩ = 2.10 3 Ω — R 2 = 16 kΩ = 16.10 3 Ω — when holding the ends of the fish, the person and the fish associate as resistors in series — applying Ohm’s 1st law — U = (R 1 + R 2 ) i — 600 = 18 .10 3 i — i = 600/18.10 3 — i=33.3. 10 -3 A — i=33.3mA — 19 mA < i < 100 mA — R- D
35- Observe the graph below where two points A and B were chosen:
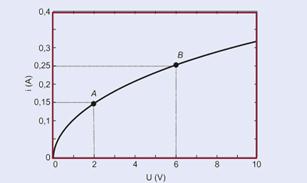
I. False — when resistance is constant, voltage and current are directly proportional, so the graph is a straight line through the origin.
II. False — Calculating the resistance for the points, A and B, highlighted in the figure — R A = U A /i A = 2/0.15 — R A = 13.3Ω — R B = U B /i B — R B = 6/0.25 — R B = 24Ω — the resistance increases with the increase in current.
III. Correct — dissipated powers for the values of the highlighted points — P A = U A . i A = 2.(0.15) = 0.3 W — P B =U B .i B —
P B =6.0.24=1.5W — P B > P A — the power dissipated in the filament increases with the increase in the applied voltage.
R-C
36- P 1 =U 2 /R — 20=24 2 /R — R=576/20 — R=28.8 Ω (assumed constant) — P 2 =U 2 /R=12 2 /28.8 — P 2 =144/28.8 — P 2 =5W — R= E
37- Note from the expression Po = U 2 /R that the dissipated power is inversely proportional to the resistance — therefore, to heat the bath water more quickly the resistance must be reduced, reducing the length of the resistor and consequently its resistance — R- C
38- 01) Correct — the dissipated power is — P d = R i 2 = 75 (2) 2 — P d = 300 W.
02) Correct — ΔE = P d .Δ t = 300 (1.4×60) — ΔE = 25,200 J.
04) Correct — addp (U) at the terminals is given by Ohm’s 1st law — U = R i = 75 (2) — U = 150 V.
08) Correct — calculating the mass of ice that melts, transforming into water — ΔE = Q = m L f — 25,200 = m (80 x 4.2) — m = 75 g — as the initial mass of ice is 0.2 kg = 200 g, 125 g of ice remains.
16) Correct — as in the end there is a mixture of water and ice, the equilibrium temperature is 0 °C.
R- (01 + 02 + 04 + 08 + 16) = 31
39-

40- I. Incorrect. If the batteries are in series, the equivalent voltage is the sum of the voltages, therefore the voltage across the flashlight bulbs will be: U = 4 +1.5 = 6 volts.
II. Correct. The energy consumed by an appliance is given by the product of the power and the operating time — flashlight — P L = 20 W — Δt L = (2.24) + 2 — Δt L = 50 h — shower — P c = 4,000 W — Δt c = 15 min = 1/4 h — W c = P c . Δt c = 4,000×1/4 —
W c = 1,000Wh = 1kWh
III. Correct.
IV. Incorrect. The compass is affected by the magnetic field created by the electric current that powers the flashlight bulbs.
R-C
41- Energy consumed — Δε = P ⋅ Δt — equating the energy consumed by the lamp with the energy consumed by the shower — Δε L = Δε C — P L ⋅ Δt L = P C ⋅ Δt C — 60 ⋅ Δt L = 6800 ⋅ 1/3 — Δt L ≈ 37.7 h — R- D
(UEPB-PB)
Read the text below to answer questions 42 and 43.
The British physicist Jaines Prescon Joule (1818-1889), who discovered the principle that bears his name, explained the relationship between electricity and heat, and brought many benefits to mankind. Many devices that we use in our daily lives work based on the Joule effect. This principle is widely used in everyday life, for example, in heating equipment such as electric irons, electric showers, straighteners, electric ovens, incandescent light bulbs, etc.
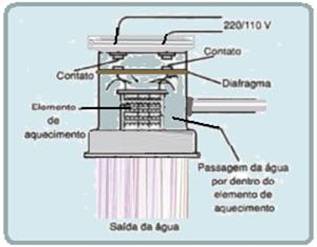
The electric shower is made up of two resistors , made up of a spiral metal wire that allows for quick and practical heating, one with high power and the other with low heating power, and a rubber diaphragm. The resistors are fixed to the inside of the shower. To select the type of shower you want to take, there is a selector switch on the outside that is capable of changing the type of resistance, increasing or decreasing the shower power and, consequently, the temperature of the shower. As the water circulates through the shower, it presses the rubber diaphragm, which in turn brings the energized contacts located in the head of the device closer together. Thus, the water heats up as it passes through the terminals of the hot resistor , making the shower nice and warm.
(Adapted from <http:/Jwwsv.newtoncbraga.com.br/index.phpieletncadomiciliar’2936-c 1033.hunl p’
To select the type of shower you want to take, the electric shower has a selector switch that can be set to the WINTER AND SUMMER positions.
42- Analyze the following theory:
In an electric shower, normally with a 220V voltage (kept constant), the winter (hot) and summer (lukewarm) positions correspond to different powers. When you change the shower cursor, for example, from summer to

In winter, you are decreasing the electrical resistance inside the shower and, consequently, increasing the power, making it hotter, of course keeping the flow constant. The opposite occurs when you change the shower cursor from winter to summer. This happens because, for the same voltage, the power is inversely proportional to the resistance, since, P=U 2 /R, with constant U.
A- A .
43- Shower power — P=6500W6.5kW — operating time — ∆t=10min=10/60=1/6hx4x30=20h — P=W/∆t — 6.5kW=W/20h — W=130kWh — R- A.
44- I- True — according to Ohm’s second law (R=ρ.ℓ/s) the electrical resistance of the filament of lamp A, which has a greater thickness S, is lower than the resistance of lamp B — the lower the resistance, the greater the brightness.
II- False — each one, after being connected in series, will be under a voltage of 220/2=110V — under a voltage of 120V they would dissipate a power of 100W, but as they are under a voltage of 110V, they will dissipate a power lower than 100W, will be traversed by a lower current, will shine less than normal, but will not burn out.
III- False — P=iU — 60=i.120 — i = 0.5 A.
R- C .
45- Amount of sensible heat used to heat m=300g of water from 20 o C to 100 o C — Q 1 =mc(t – t o )=300.1.0.(100 – 20) —
Q 1 =300.1.0.80 — Q 1 =24,000cal — amount of latent heat used to vaporize m/3=100g of water at 100 o C — Q 2 =mL V — Q 2 =100,540 — Q 2 =54,000cal — amount of total heat absorbed by the water — Q total =Q 1 + Q 2 =78,000cal —
by the statement all electrical energy is transformed into thermal energy — electrical energy (W) — 1cal — 4.2J — 78,000cal — WJ — W=327,600J — electrical power of the vaporizer — P o =Ri 2 =12.10 2 — P o =1,200W — P o =W/∆t — 1,200=327,600/∆t — ∆t=273s/60=4min 33s — R- B
46- (ENEM-MEC)
From the statement, the two showers are operating at the same power — P A = P B = 4400W — Shower A — P A = 4,400W — U A = 127V — P A = U A 2 / R A — 4400 = 127 2 / R A — R A = 16129/4400=3.665Ω — Shower B — P B = 4,400W — U B = 127V — P B = U B 2 / R B — 4400=220 2 / R B — R B = 48400/4400=11Ω — the exercise asks for R A / R B = 3.665/11=0.33 — R- A .
