Resistor equivalente – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Resistor equivalente

 01- a) Veja figura abaixo, onde os resistores de 2 Ω, 4 Ω e 4 Ω estão associados em paralelo  —  4 com 4=4/2=2 Ω  —  2 com

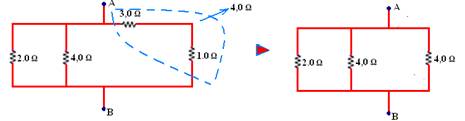
2=2/2=1 Ω  —  R_eq=1 Ω

b)

c)

 

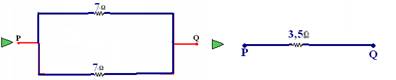
d)

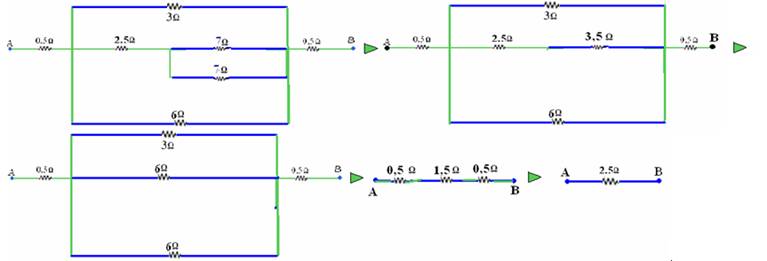
e)

f)

g)

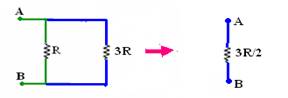
h)

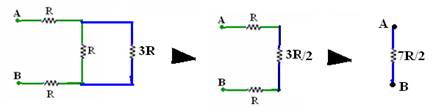
i)

j)

 

 

l)

 

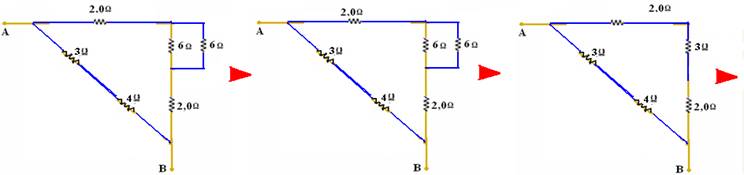
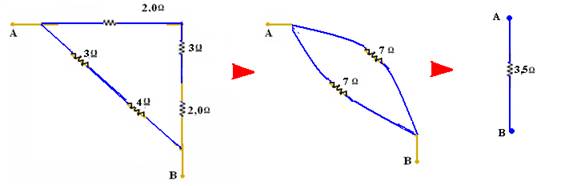
02-

03-

R- B

04- R- A  —  R/5

05- Correta  —  R₂ paralelo com R₃  — R’=20/5=4Ω  —  R’ série com R₁  —  R_eq1=20 + 4=24Ω  —  errada  —  R₂ paralelo com R₃ =20/2=10Ω —  10Ω em série com R₁  —  R_eq2=10 + 5=15Ω  —  diferença  —  R=24 – 15=9Ω  —  R-B

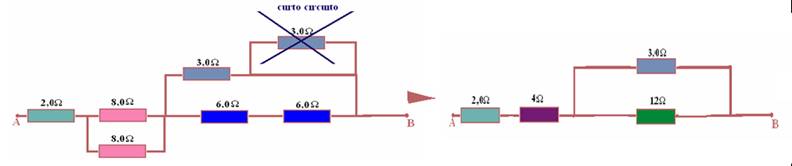
06- Observe as resoluções nas figuras abaixo:

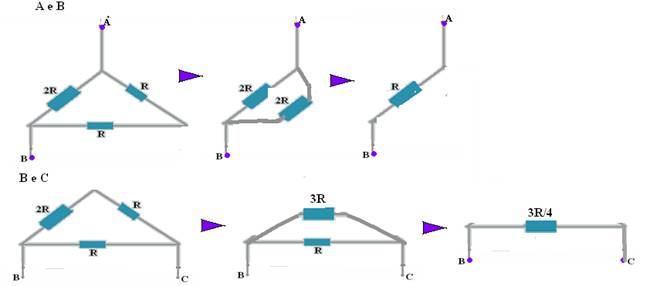
 R_AB/R_BC=R/1 x 4/3R=4/3  —  R- A

07- a)

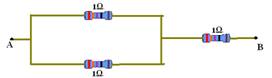
b) Como o número de resistores não foi especificado, existem várias associações cuja resistência equivalente é 1,5Ω  —  uma delas está no esquema abaixo

08- A) Sim, é ôhmico, pois o gráfico Uxi é uma reta inclinada a partir da origem, ou seja , U é  proporcional a i de modo que R seja constante  —  R=U/i=0,6/0,2=1.2/0,4=3,0/1,0=3Ω

B) R=U/i  —  3=9/i  —  i=3A   —  P_o=i.U=3.9=27W  —  W=P_o..Δt=27.300  — W=8.100J=8,1kJ

C) È a associação I onde a resistência equivalente é menor (R/2), dissipando assim, maior potência.

09- (5 + R) paralelo com 4Ω  —  R_eq=produto pela soma  —  3=(5 + R).4/5 + R + 4  —  3=(20 + 4R)/9 + R  —  27 + 3R=20 + 4R  —  R=7Ω  —  R- E

10- série  —  R_eq=R₁ + R₂  —  6=R₁ + R₂  —  R₁=6 – R₂ (I)  —  paralelo  —  R_eq=R₁.R₂/(R₁ + R₂)  —  4/3=R₁.R₂/(R₁ + R₂)  —  3R₁R₂=4R₁ + 4R₂ (II)  — (I) em (II)  —  3.(6 – R₂).R₂=4(6 – R₂) + 4R₂  —  3R₂² – 18R₂ + 24=0  —  resolvendo essa equação, obtém-se 2Ω e 4Ω  —  R- C

11- R- B  —  veja teoria

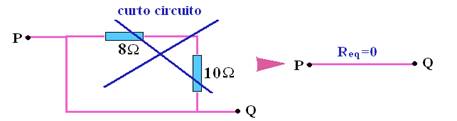
12- R_eq=30/3=10 Ω  —  R- A

13-

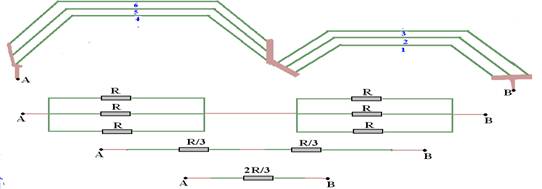
14- Observe nas figuras abaixo a seqüência de operações:

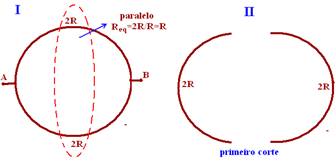
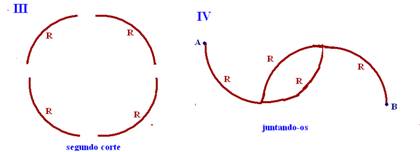
Os dois que estão em paralelo  —  R’=R/2  —  R’ fica em série com R e R  —  R_eq=R + R/2 + R  —  R_eq=5R/2  —  R- E

15- O sistema que aquece mais rapidamente a água é aquele que possui menor resistência equivalente  —  R_eq=0,5Ω  —  R- B

16- a) chave fechada  —  todos os resistores são percorridos por corrente e participam do circuito  —  R paralelo com R – R/2  —  R/2 em série com R  —  R_eq=3R/2=1,5R  — R_eq=U/i  —  1,5R=U/i  —  i=U/1,5R  —  chave aberta  —  passa corrente apenas pelos dois resistores que estão em série  —  R’_eq=2R  —  R’_eq=U/i’  —  2R=U/i’  —  i’=U/2R  —  i’/i=U/2R x 1,5R/U=1,5/2  —  i’/i=0,75.

b) Com a chave fechada onde a resistência equivalente é menor, dissipando maior potência e aquecendo mais a água.

17- Como o resistor maior é o A e ele vai ser somado com o R_eq dos outros dois, a alternativa correta é a D  —  R- D

18- R- C  —  R_eq=R/3

19- R₂ é a menor resistência, tem o maior   —  série  —  R₁ + R₂=R (I)  —  paralelo  —  R₁.R₂/(R₁ + R₂)=3R/16  —   R₁.R₂/R=3R/16  —  R₁.R₂=3R²/16 (II)  —  resolvendo o sistema composto por (I) e (II)  —  R₁=R/4 e R₂=3R/4

20- Para que a potência dissipada seja a menor possível, a resistência equivalente deve ser a maior possível, o que ocorrerá quando eles forem ligados em série  —  R_eq=1 + 2=3  —  R_eq=3 Ω  —  P_o=U²/R_eq=4/3W  —  R- A

21- Maior corrente implica em maior potência e consequentemente em menor resistência  — R- D

22- a) menor potência implica em maior resistência equivalente, no caso, em série  —  R_eq=2 + 6=8Ω  —  potência dissipada  —  P_o=U²/R_eq=144/8  —  P_o=18W

b)

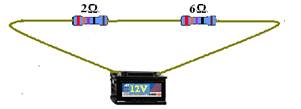
c) Sendo P_o=U²/R_eq  —  U² é diretamente proporcional a P_o  —  para que a potência fique 4 vezes maior, a tensão U deve ser dobrada  —  U=2.12  —  U=24V

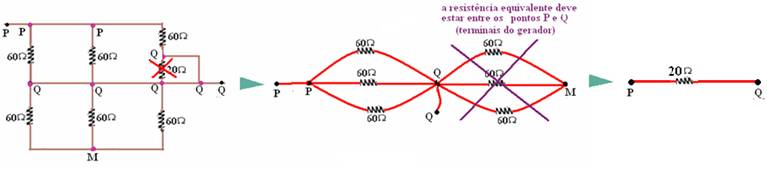
23- Refazendo o circuito e chamando de P e Q na figura abaixo os pontos de interseção de fios:

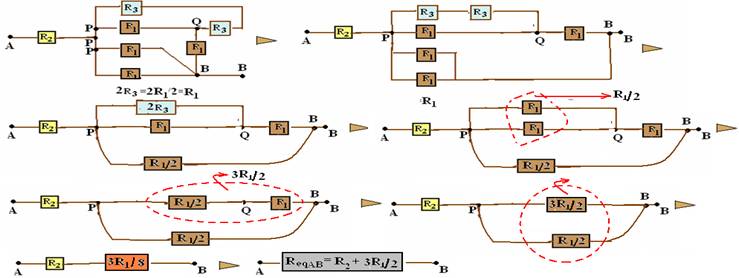
Como R_eqAB=2R₂  —  2R₂=R₂ + 3R₁/9  —  R₂=3R₁/8  —  R₂/R₁=3/8  —  R- A

24- Chamando de r a resistência equivalente dos infinitos resistores que estão a direita dos pontos P e Q (região delimitada em

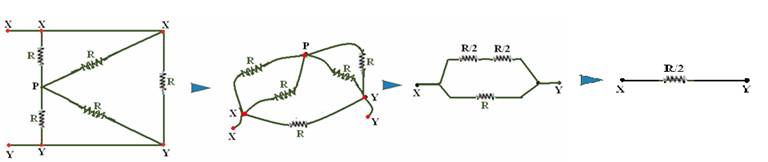
vermelho)  —  lembre-se que,se a seqüência é infinita, a resistência da seqüência situada à direita dos pontos P e Q também é r, e então pode-se fazer —  r = r paralelo com R (r’) + r’ em série com 2R  —  r= r.R/(r + R) + 2R  —  r(r + R) = rR + (r + R).2R  —  r² + rR = rR + 2Rr + 2R²  —  r² – 2Rr – 2R²=0  —  Δ=B² – 4.A.C=4R² – 4.1.(-2R²)  — 

Δ=4R² + 8R²=12R²  —  √Δ=2√3R  —  r₁= (2R  + 2√3R)/2  —  r₁=R(1 + √3) e r₂=R(1 – √3)  —  r₂ não satisfaz por ser negativa  —

R- E

25- lado oeste  —   cada km tem 13Ω de resistência  —  13x + R + 13x=60  —  26x + R=60  —  R=60 – 26x (I)  —  lado leste  — 

13.(10 – x) + R + 13.(10 – x)=216  —  130 – 13x + R + 130 – 13x=216  —  -26x + R=-44 (II)  —  (I) em (II)  —  -26x + (60 – 26x)=-44  —  -52x=-104  —  x=2km  —  R- A

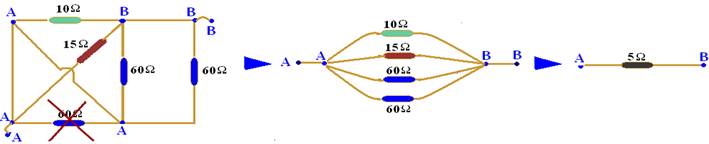
26- Observe que os dois resistores estão entre os pontos P e Q  —  paralelos  —  R_eq=20/3=6,66Ω  —  R- B

27- Cálculo da resistência de cada lâmpada  —  P_o=U²/R  —  40=(120)²/R  —  R=360Ω  —  cálculo do valor da resistência equivalente das 4 lâmpadas associadas em paralelo  —  R_eq=360/4  —  R_eq=90Ω  —  cálculo da potência total fornecida por essas 4 lâmpadas em paralelo (uma chocadeira)  —  P_ot=U²/R_eq=(120)²/90  —  P_ot=160W  —  cálculo da energia consumida por essa chocadeira em um dia  —  W=P_ot.Δt=160W.1dia  —  W=160W por dia ou W=0,16kW por dia  —  hidrelétrica fornece 24kW por dia  —  chocadeira consome 0,16kW por dia  —  número de chocadeiras  —  n=24/0,16  —  n=150 chocadeiras por dia  —  R- A

28- a)

b)

c)

29-

R- C

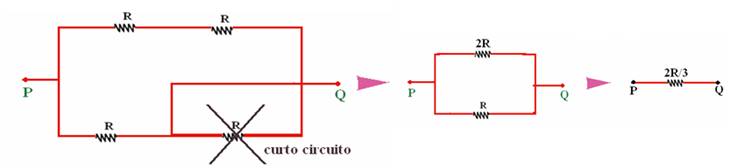
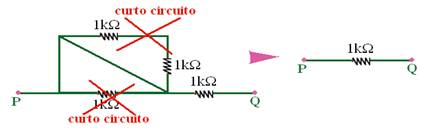
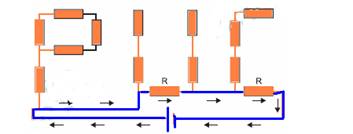
30- Só são iluminados os trechos percorridos por corrente  —  os trechos que estão em curo circuito foram eliminados nas figuras abaixo

R- E

31-

 

32– Observe na figura abaixo que todos os pontos B estão em curto circuito, ou seja, são coincidentes e o mesmo ocorre com todos

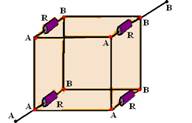
os pontos A  —  então os 4 resistores estão em paralelo  —  R_eq=R/4  —  R_eq=U/i  —  R/4=U/i  —  i=4U/R  —  R- A

33- Marcando os nós e colocando letras:

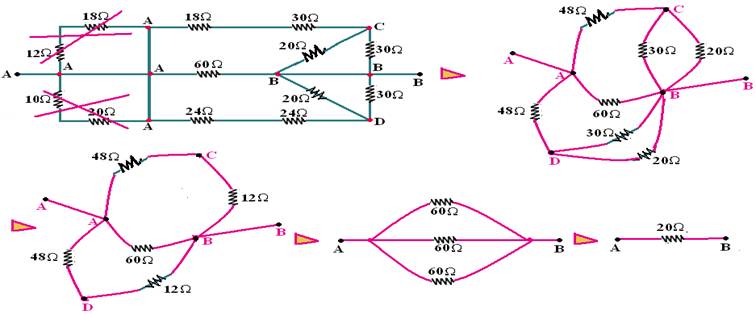
R- B

34- a)

 

b)

c)

35-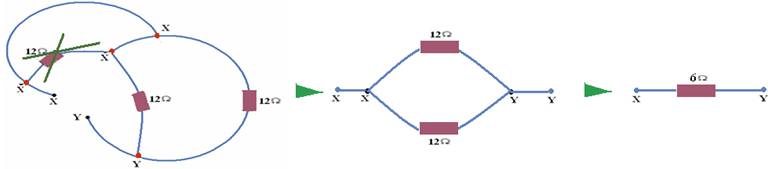 

36-

37-

R- B

38-

 

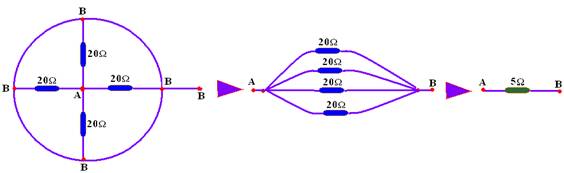
39- Observe que, por simetria, os três pontos da reta vertical tem o mesmo potencial  — 

40- Observe que existe um curto circuito e que a corrente passará somente pelos dois resistores de baixo  —  R_eq=R + R=2R

R_eq=2R

41-

R- A

42- Resistência equivalente R dos três resistores de resistências a, b e c, associados em paralelo  —  1/R=1/a + 1/b + 1/c  —  esses valores estão em progressão geométrica  —  b/a=c/b=1/2  —  a=2b  —  c=b/2  — do enunciado  —  R=2Ω  —  ½=1/2b + 1/b +1/(b/2)  —  1/2=1/b(1/2 + 1 + 2)=7/2b  —  b=7Ω  —  a=2b=2.7=14Ω  —  c=b/2=7/2=3,5Ω  —  (a + b + c)=(7 + 14 + 3,5)=24,5Ω
R- D

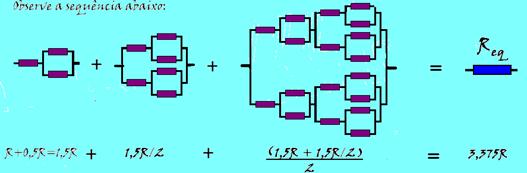
43- Veja a seqüência abaixo:

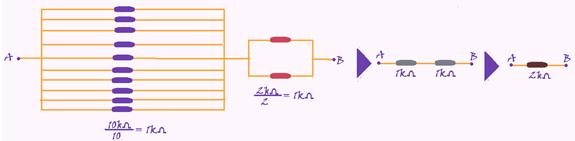
R- B

44- A resistência entre A e B corresponde à soma de R com a associação em paralelo entre R e R_eq (restante do circuito)  —

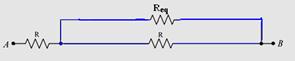
R_AB= R + R,R_eq/(R + R_eq)  —  R_AB=R_eq já que o padrão do circuito se repete ao infinito e os dois são tão grandes que podem ser igualados  —  R_AB= R + R. R_AB/(R + R_AB)  — 

R²_AB – R. R_AB – R²=0  —  R_AB=(R + R√5)/2  —  R_AB=(R – R√5)/2 (excluído, pois R_AB deve ser positivo)  —  R_AB=R( 1 + √5)/2  —

R- D

45- Refazendo o circuito:

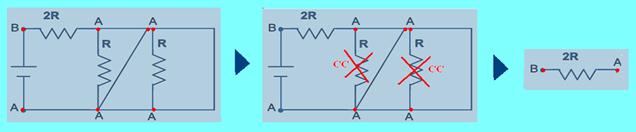
R- B

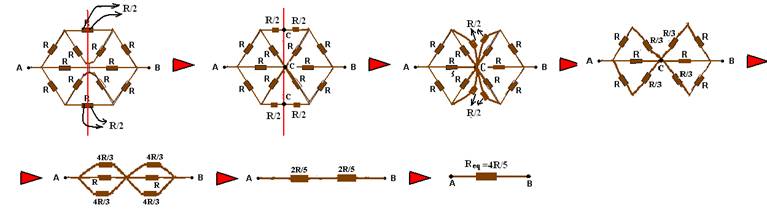
46- Observe a sequência abaixo:

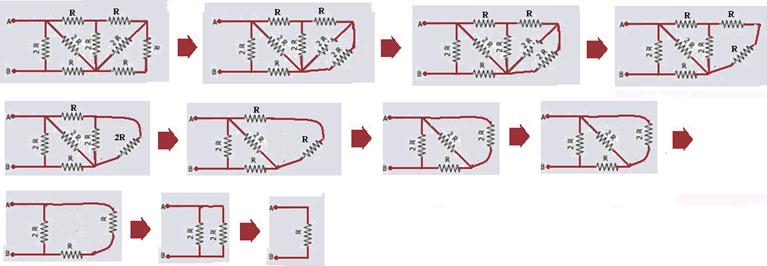
R- B

47- Observe a  sequência de figuras abaixo:

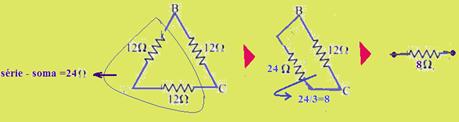
R- B

48- Observe a seqüência abaixo:

R- B

 

Voltar para os exercícios