Resistor equivalente

 

 Resistor equivalente

Resistor equivalente (R_eq)  Muitas vezes você deve substituir um resistor de determinado valor nominal, num circuito elétrico, mas não o possui.

No entanto você pode substituí-lo por uma associação de resistores que possua o mesmo valor nominal. Essa associação recebe o nome de resistor equivalente (R_eq) da associação, que é aquele que, submetido à mesma diferença de potencial da associação, é percorrido pela mesma corrente, não alterando as características do circuito.

 

Resistor equivalente na associação série

Uma  associação série é aquela em que os resistores estão associados um em seguida do outro de modo que a corrente em cada um seja a mesma.

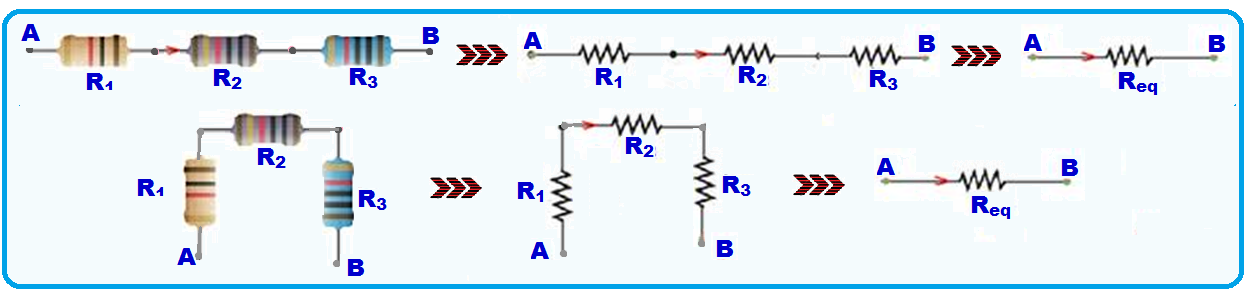
Cálculo da resistência (R_eq) do resistor equivalente na associação série a  resistência do resistor equivalente entre A e B é fornecida pela soma das resistências de cada resistor.

Exemplos numéricos:

Resistor equivalente na associação paralelo

A associação paralelo é aquela em que  os resistores são associados pelos seus terminais, ou seja, todos saem do mesmo ponto (A) e todos chegam ao mesmo ponto (B).

Cálculo da resistência (R_eq) do resistor equivalente na associação paralelo:

Três processos:

3^o – Regra prática:

 quando um é o dobro do outro, você pega o maior e divide por três;

  quando um é o triplo do outro, você pega o maior e divide por quatro, e assim por diante.

 dois resistores iguais, você divide o valor de um deles por dois;

   três resistores iguais, você divide o valor de um deles por três, e assim por diante. 

Em alguns casos essa regra prática, quando o número não der exato, pode ser substituída por uma das duas acima.

Exemplo numérico:

1^o processo:

Se você invertesse a ordem, o resultado seria o mesmo:

Resistor equivalente na associação mista

 Associação Mista  consta de uma combinação das associações série e paralelo, cujo cálculo você deve fazer por partes até chegar a um único resistor equivalente R_eq.

Para isso deve-se ir substituindo cada associação parcial, série ou paralelo, por um único resistor e ir diminuindo aos poucos o esquema da associação.

Analise detalhadamente esses exemplos:

Em cada caso abaixo, calcule a resistência equivalente entre os pontos P e Q.

01-

02-

   

 

03- Veja bem, os três últimos estão em série, comece por eles:

 Quer se aprofundar mais? Veja, com as respectivas resoluções os exercícios 01 (d, e, i, j e l); 06; 13 e 33.

O que você deve saber, informações e dicas

Cálculo da resistência (R_eq) do resistor equivalente na associação paralelo:

Três processos:

3^o – Regra prática:

 quando um é o dobro do outro, você pega o maior e divide por três;

  quando um é o triplo do outro, você pega o maior e divide por quatro, e assim por diante.

 dois resistores iguais, você divide o valor de um deles por dois;

   três resistores iguais, você divide o valor de um deles por três, e assim por diante. 

Em alguns casos essa regra prática, quando o número não der exato, pode ser substituída por uma das duas acima.

 Quanto menor for a resistência equivalente de uma associação de resistores, maior será a potência dissipada por ela de modo que sua eficiência seja maior   justificativa  P_o=U²/R_eq    observe que a potência é inversamente proporcional à resistência equivalente.

Disjuntores

 Disjuntores  A função do disjuntor é interromper automaticamente a passagem da corrente elétrica por um dos pontos (cômodos) da residência, quando suaintensidade excede determinado valor (a chave desliga).

Se a chave do disjuntor, com o excesso de corrente elétrica não desligasse, os fios do circuito seriam muito aquecidos podendo fundir, causando incêndios.

Junto aos disjuntores, na caixa de luz, existe um quadro identificador dos cômodos ou pontos atendidos por cada disjuntor, como por exemplo, iluminação, tomadas, chuveiros, etc..

Reostatos

 Reostatos são resistores variáveis cuja finalidade é adaptar a intensidade da corrente elétrica a valores desejados.

Tipos de reostatos:

Os principais tipos de reostatos são    reostato de cursor  variando o cursor você está

variando a resistência (figura 1)    reostato de pontos em cada posição da chave aresistência elétrica tem um determinado valor (figura 2).

Curto circuito (CC)

 

 Quando se liga (une) dois pontos de um circuito elétrico por um condutor (fio) de resistência desprezível (fio ideal, fio sem resistência), diz-se que esses dois pontos ficam em curto circuito (CC).

Considere um resistor R sendo percorrido por uma corrente elétrica i e submetido a uma diferença de potencial U_AB = V_A – V_B.

Ligando-se, em paralelo, entre os pontos A e B desse resistor, um condutor de resistência desprezível (fio ideal), provoca-se um curto circuito entre A e B e verifica-se que toda a corrente elétrica se desviará, passando pelo fio ideal, no qual, aplicando-se a lei de Ohm ter-se-á    V_A – V_B = U_AB = R.i    comoR = 0 (fio ideal), tem-se    V_A – V_B = R.i    V_A – V_B = 0.i    V_A – V_B = 0    V_A = V_B.

Assim, o circuito se comporta como se o resistor não existisse e pode-se redesenhar o circuito, tornando os pontos A e B coincidentes.

Exemplos de cálculo do valor da resistência (R_eq) do resistor equivalente, com curto-circuito (CC)

Calcule, em cada caso, a resistência do resistor equivalente entre os pontos A e B:

a)

b)

        

c)

 

 

Cálculo do resistor equivalente em casos mais complexos de curto-circuito

 Em alguns casos de curto circuito mais complexos, não é possível visualizar a situação (os pontos em curto-circuito) e é preciso refazer o circuito, procedendo da seguinte maneira prática:

1^o  Marcar todos os nós da associação (nó – ponto de cruzamento de 3 ou mais fios ).

2^o  Colocar letras em cada nó, lembrando que os pontos unidos por fio ideal (nós) estão em curto circuito e devem ser nomeados a mesma letra, pois possuem o mesmo potencial.

3^o  Refazer o circuito

 

Exemplos de cálculo do valor da resistência (R_eq) do resistor equivalente, com curto-circuito (CC), refazendo o circuito

Determine, em cada caso, entre os pontos P e Q, a resistência equivalente de cada associação:

a)

Etapas: Preste muita atenção nas etapas da resolução.

 Refazendo o circuito

Os resistores entre os pontos P e P, unidos pela mesma letra, estão em curto circuito não colocar os resistores de 5Ω e 30 Ω    entre P e B tem um de 30 Ω e um de 8 Ω    entre B e Q tem

um de 10Ω    veja esquema e seqüência acima.

c)

Observação: Se você quiser aprofundar mais, analise os exercícios 26; 28(c); 29; 30; 34(c) e 35, com as respectivas resoluções.

 

Confira os exercícios com resolução comentada