EN equivalent resistor
EQUIVALENT RESISTOR
Equivalent resistor
Equivalent resistor ( Req ) Many times you need to replace a resistor of a certain nominal value in an electrical circuit, but you don’t have it. 
However, you can replace it with an association of resistors that has the same nominal value. This association is called the equivalent resistor (Req ) of the association, which is the one that, subjected to the same potential difference as the association, is traversed by the same current, without altering the characteristics of the circuit.
Equivalent resistor in series association
A series association is one in which resistors are associated one after the other so that the current in each is the same.
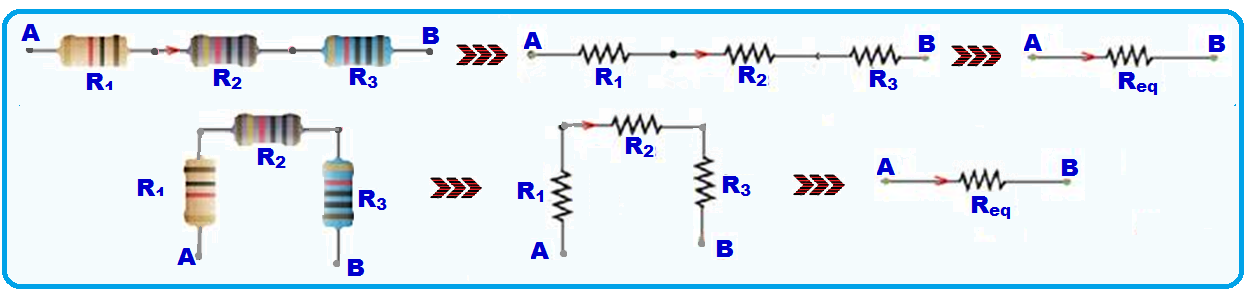
Calculation of the resistance (R eq ) of the equivalent resistor in the series association the resistance of the equivalent resistor between A and B is given by the sum of the resistances of each resistor.
Numerical examples:
Equivalent resistor in parallel association
Parallel association is one in which the resistors are associated by their terminals , that is, they all leave from the same point (A) and all arrive at the same point (B).
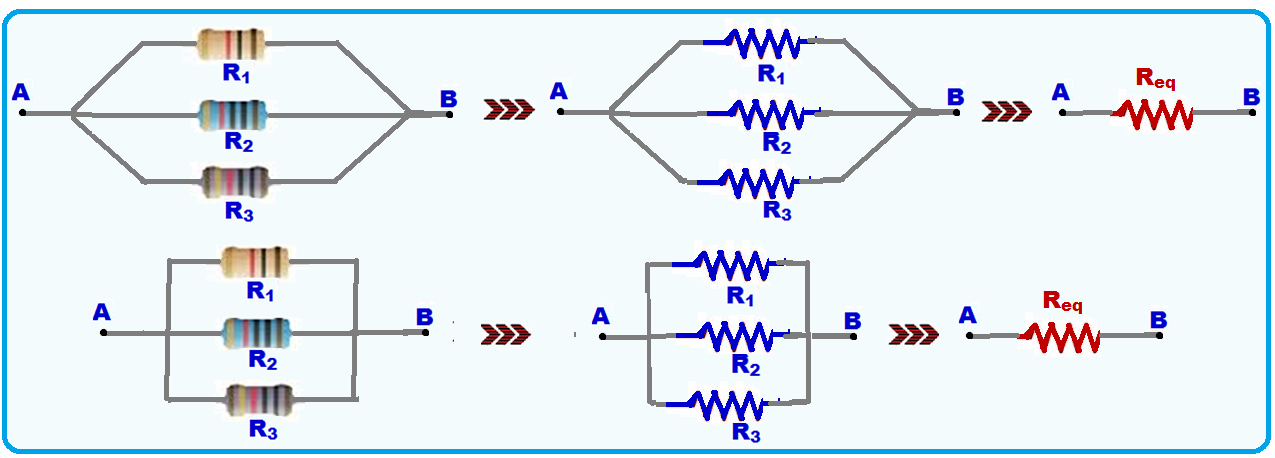
Calculation of the resistance (R eq ) of the equivalent resistor in parallel association:
Three processes:
3rd – Practical rule :
when one is twice the other, you take the larger one and divide it by three;
when one is three times the other, you take the larger one and divide it by four, and so on.
two equal resistors , you divide the value of one of them by two;
three equal resistors , you divide the value of one of them by three, and so on.
In some cases this rule of thumb, when the number is not exact , can be replaced by one of the two above.
Numerical example:
1st process :
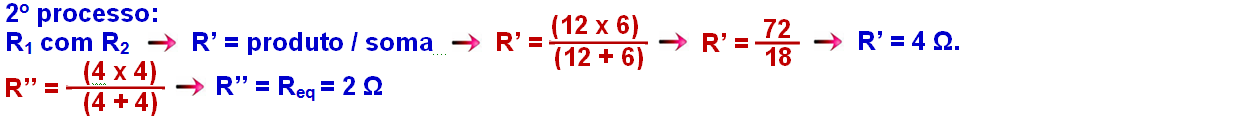
If you reversed the order, the result would be the same:
Equivalent resistor in mixed combination
Mixed Association consists of a combination of series and parallel associations, which you must calculate in parts until you reach a single equivalent resistor R eq .
To do this, you must replace each partial association, series or parallel , with a single resistor and gradually reduce the association scheme.
Analyze these examples in detail:
In each case below, calculate the equivalent resistance between points P and Q.
01-
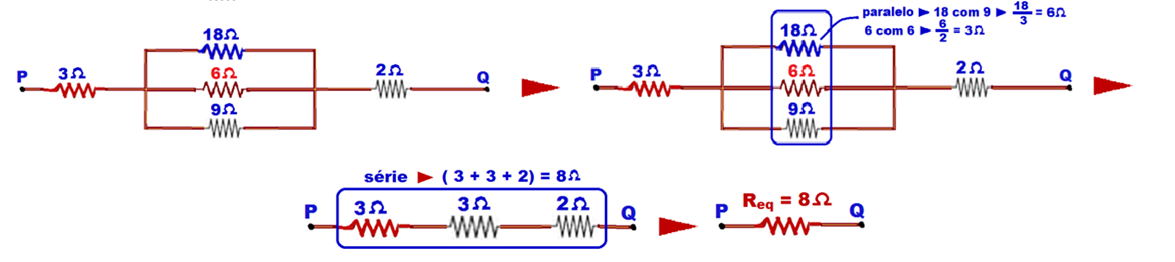
02-
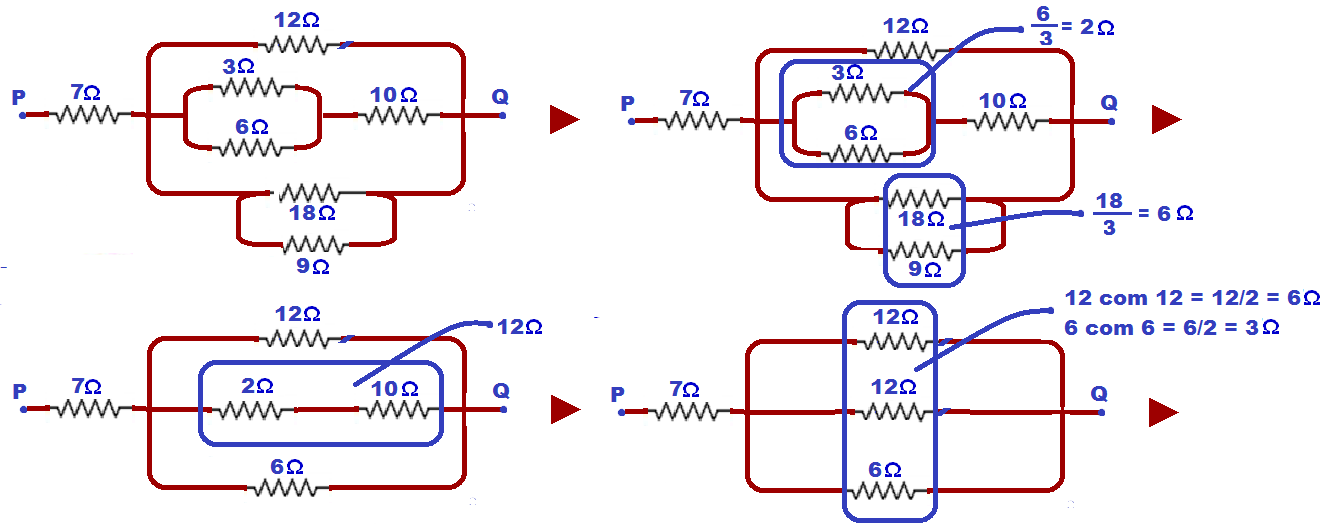
03- Look, the last three are in series, start with them:
Want to learn more? See exercises 01 (d, e, i, jel); 06; 13 and 33 with their respective solutions.
What you should know, information and tips
Calculation of the resistance (R eq ) of the equivalent resistor in parallel association:
Three processes:
3rd – Practical rule :
when one is twice the other, you take the larger one and divide it by three;
when one is three times the other, you take the larger one and divide it by four, and so on.
two equal resistors , you divide the value of one of them by two;
three equal resistors , you divide the value of one of them by three, and so on.
In some cases this rule of thumb, when the number is not exact , can be replaced by one of the two above.
The lower the equivalent resistance of a resistor association, the greater the power dissipated by it, so that its efficiency is greater. Justification P o = U 2 /R eq Note that the power is inversely proportional to the equivalent resistance. 
Circuit breakers
Circuit breakers The function of the circuit breaker is to automatically interrupt the passage of electrical current through one of the points (rooms) of the residence , when its intensity exceeds a certain value (the switch turns off).
If the circuit breaker switch did not turn off due to the excess electrical current , the circuit wires would become very hot and could melt, causing fires.
Next to the circuit breakers, in the electrical box, there is a panel identifying the rooms or points served by each circuit breaker, such as lighting, sockets, showers, etc.
Rheostats
Rheostats are variable resistors whose purpose is to adapt the intensity of the electric current to desired values.
Types of rheostats:
The main types of rheostats are cursor rheostat varying the cursor you are 
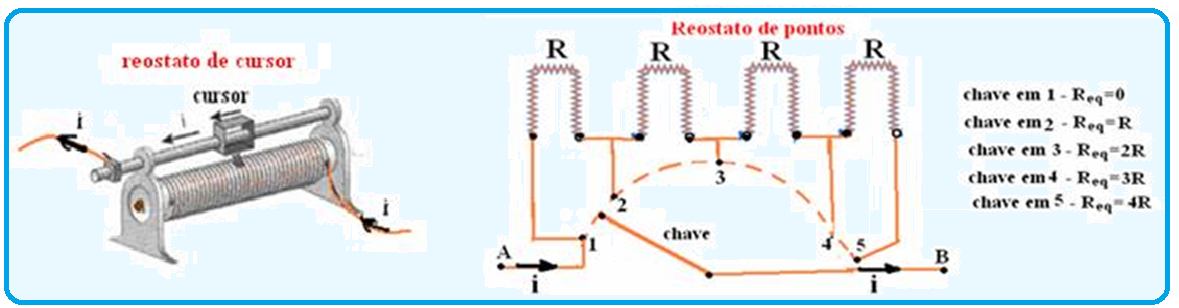varying the resistance (figure 1) point rheostat in each position of the switch the electrical resistance has a certain value (figure 2).
Short circuit (DC)
When two points of an electrical circuit are connected (joined) by a conductor (wire) of negligible resistance (ideal wire, wire without resistance), these two points are said to be in a short circuit (CC).
Consider a resistor R being traversed by an electric current ie subjected to a potential difference U AB = V A – V B.
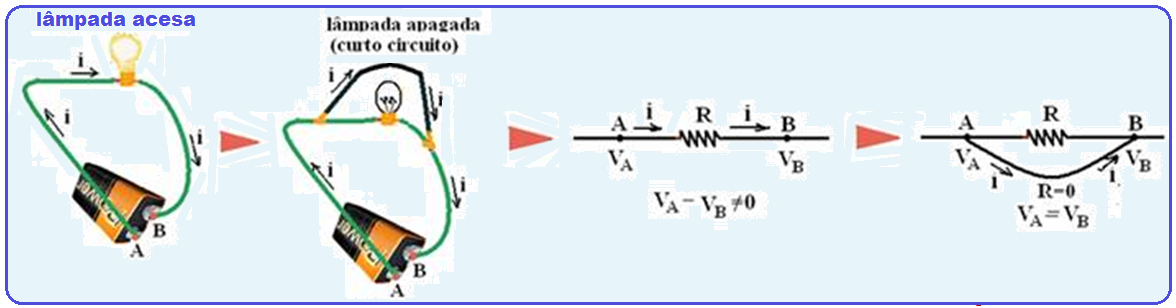
By connecting, in parallel, between points A and B of this resistor , a conductor of negligible resistance (ideal wire), a short circuit is caused between A and B and it is verified that all the electric current will be diverted, passing through the ideal wire , in which, applying Ohm’s law, we will have V A – V B = U AB = Ri as R = 0 (ideal wire), we have V A – V B = Ri V A – V B = 0.i V A – V B = 0 V A = V B.
Thus, the circuit behaves as if the resistor did not exist and the circuit can be redesigned, making points A and B coincident.
Examples of calculating the resistance value (R eq) of the equivalent resistor, with short circuit (CC)
Calculate, in each case, the resistance of the equivalent resistor between points A and B:
the)
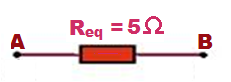
b)
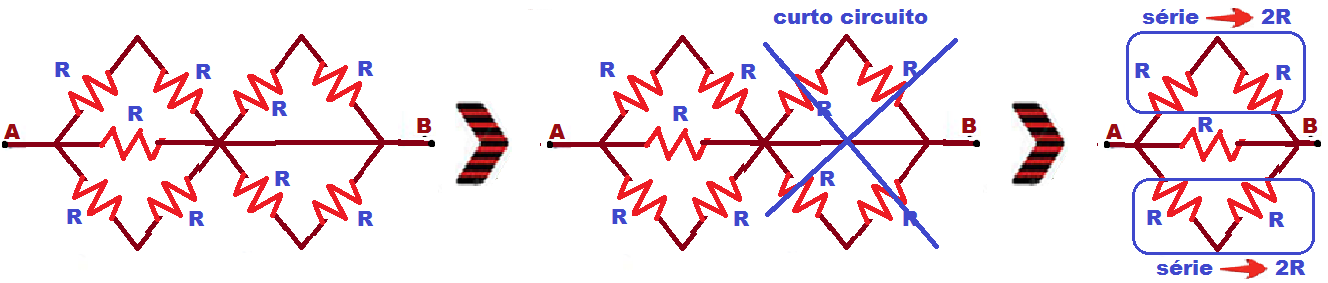
w)
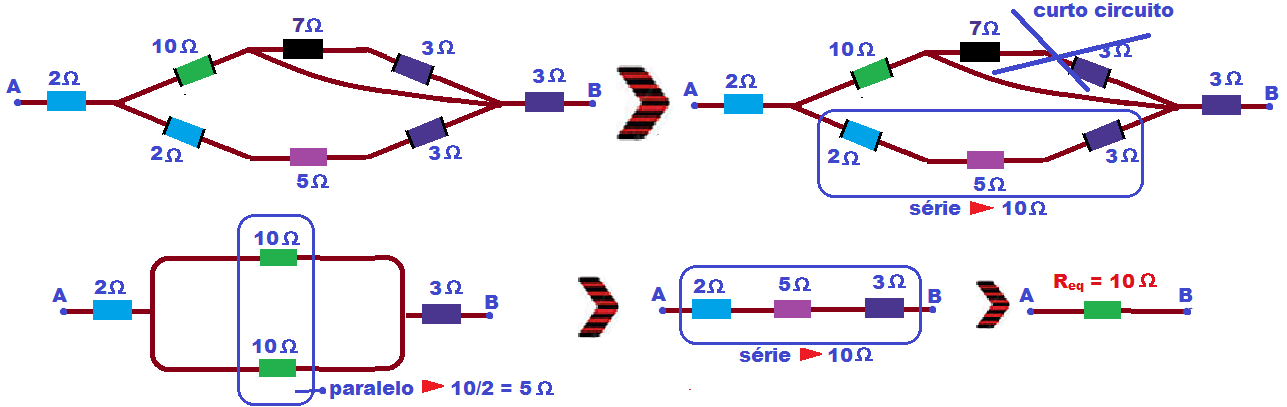
Calculation of the equivalent resistor in more complex short-circuit cases
In some more complex short-circuit cases , it is not possible to visualize the situation (the short-circuited points) and it is necessary to redo the circuit , proceeding in the following practical manner:
1st Mark all the nodes of the association (node – crossing point of 3 or more wires) . 
2. Place letters on each node, remembering that the points joined by an ideal wire (nodes) are in a short circuit and must be named with the same letter , as they have the same potential. 
3. Redo the circuit
Examples of calculating the resistance value (R eq) of the equivalent resistor, with short circuit (CC), redoing the circuit
Determine, in each case , between points P and Q, the equivalent resistance of each association:
the)
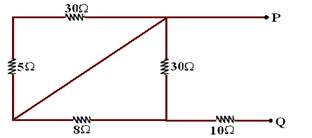
Steps: Pay close attention to the steps of the resolution.
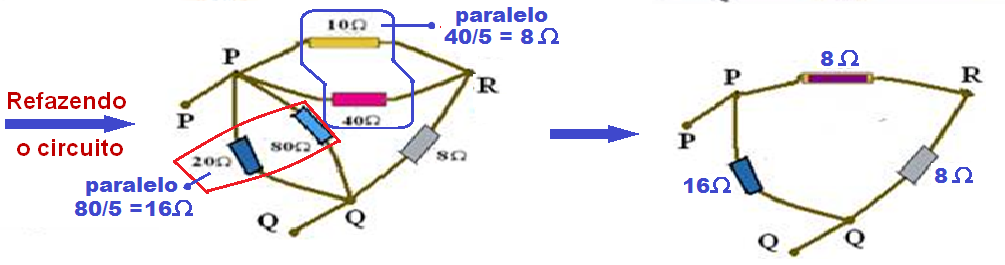
Remaking the circuit
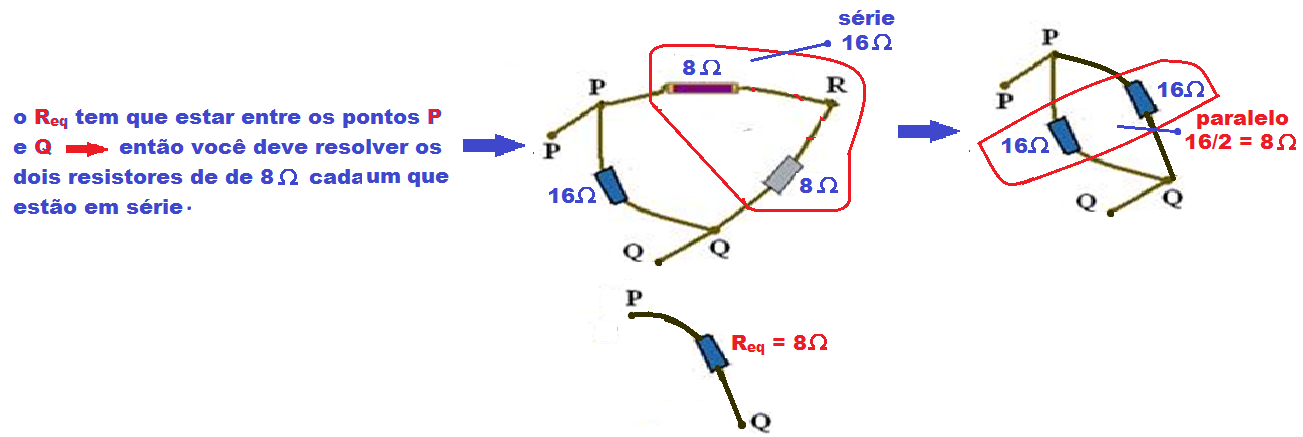
The resistors between points P and P , joined by the same letter, are in short circuit. Do not place the 5Ω and 30Ω resistors between P and B. There is one of 30Ω and one of 8Ω between B and Q. 
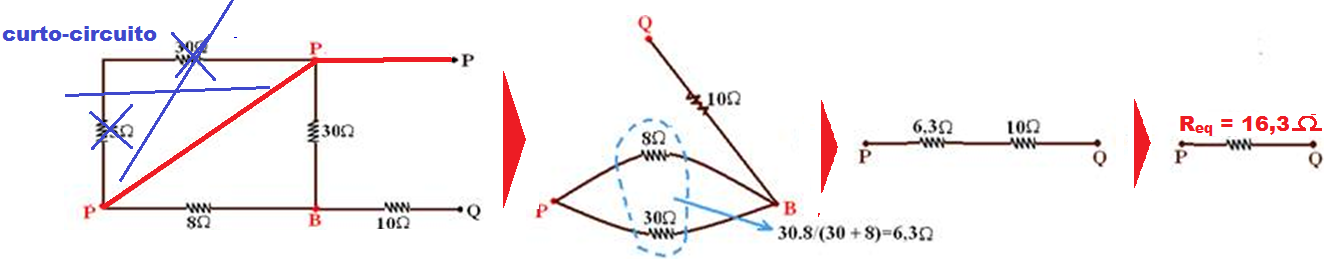
one of 10Ω see diagram and sequence above.
w)
Note: If you want to go deeper , analyze exercises 26; 28(c); 29; 30; 34(c) and 35, with their respective solutions.