Receptores – Associação de geradores com receptores – Lei de Pouillet – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Receptores – Associação de geradores com receptores – Lei de Pouillet

01- j Quando i=2A — U=22V — U=E’ + r’.i — 22=E’ + r’.2 (I) — quando i=5 A — U=25V — U=E’ + r’.i — 25=E’ + r’.5 (II) — resolvendo o sistema composto por (I) e (II) — R- C

02- a) Cálculo da corrente elétrica no receptor — P_t=i.U — 1.600=i.200 — i=8A — P_d=r’.i²=10.(8)² — P_d=640W

b) Potência útil — P_t=P_d + P_u — 1.600=640 + P_u — P_u=960W — P_u=E’.i — 960=E’.8 — E’=120V

c) η=E’/U=120/200=0,6 — η=60%

03- a) Equação do receptor — U=E’ + r’.i — 50=E’+1.2,5 — E’=47,5V

b) O voltímetro indica o valor da força contra-eletromotriz do receptor — U=50V

04- Equação do receptor — U=E’ + r’.i — 440=E’ + 25.0,4 — E’=440 – 10 — E’=430V — R- D

05- O gráfico do gerador é o da reta descendente — icc=20A — icc=E/r — 20=E/r — E=20r —

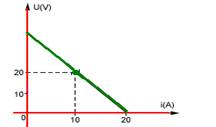
Equação do gerador — quando i=10A – U=20V — U=E – r.i — 20=E – r.10 — 20=20r – 10r — r=2Ω — E=20r=20.2 — E=40V

O gráfico do receptor é o da reta ascendente — observe que E’=10V — quando 1=10A – U=20V — equação do receptor —

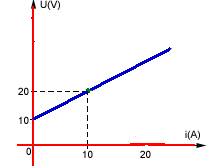
U=E’ + r’.i — 20=10 +r’.10 — r’=10/10 — r’=1Ω — R- D

06- Chave aberta — se você ligar um voltímetro ideal (resistência interna infinita) nos terminais de um gerador ele indicará sua força eletromotriz (no caso E=20V), pois ele funciona como se estivesse em circuito aberto — se você ligar um voltímetro nos terminais de um receptor desligado (chave k aberta) como por exemplo de um liquidificador, ferro elétrico, etc., ele indicará zero Chave fechada — circulará corrente de valor — i=(∑E – ∑E’)/∑R=(20 – 15)//(3 + 2) — i=1A — cálculo de U_AB pelo gerador — U_AB=E – r.i=20 – 3.1 — U_AB=17V — U_AB=E’ + r’.i=15 + 2.1 — U_AB=17V — R- B

07- a) i=(3 – 1,5)/((10 + 20) — i=0.05A

b) pelo gerador — U=E – r.i=3 – 20.0,05 — U=2V — ou, pelo receptor — U=E’ + r’+.i=1,5 + 1=.0,05 — U=2V

c) Haverá desgaste da pilha de maior fem, que é a de 3V — Observação — esse tipo de ligação é inconveniente, pois sempre haverá corrente entre elas com a de 3V funcionando como gerador e fornecendo corrente para a de 1,5V que funciona como receptor. Então, o desgaste é inevitável.

08- Resolvendo R₂ paralelo com R₃paralelo com R₄ para chegar à uma malha única — R’=2Ω — i=(4 – 2)/(2 + 0,5 + 0,5 + 2) — i=2/5 — i=0,4 A — U=R’.i=2.0,4 — U=0,8V

09- Deixando uma malha única — 20 Ω paralelo com (10 Ω + R) — R’=20.(10 + R)/20 + 10 + R — R’=(200 + 20R)/(30 + R) — i=(55 – 5)/(200 + 20R)/(30 + R) + 10 — 2=50/(500 + 30R)/(30 + R) — 1.000 + 60R=1.500 + 50R — R=50Ω

10- Observe que o sentido da corrente é no horário — i=(+6 +6 -2)/(4 + 2 +4) — i=10/10 — i=1A — R=U/i — 2=U/1 — U=2V

11- i=(12 – 6)/(4 + 2) — i=1A — pelo gerador (E=12V e r=2Ω) — U_AB=E – r.i=12 – 2.1 — U=10V — ou, pelo receptor (E’=6V e r’=4Ω) — U=E’ + r’.i=6 + 4.1 — U=10V — observe que V_B é maior que V_A — V_B – V_A=10 — 15 – V_A=10 — V_A=5V

12- entre A e B — U_AB=V_A– V_B — U_AB=R.i=2.2 — U_AB=4V — V_A – V_B=4 — 4 – V_B= 4 — V_B=0 — gerador — V_C > V_B — U_CB=E₁ – r₁.i=10 – 0,5.2 — U_CB=9V — V_C – V_B=9 — V_C – 0 = 9 — V_C=9V — receptor — V_C > V_D — U_CD=V_C – V_D — U_CD=E₂ + r₂.i=3 + 1.2 — U_CD=5V — U_CD= V_C – V_D — 5=9 – V_D — V_D=4V — R- A — Observe que V_A=V_D (unidos por fio ideal)

13- Substituindo os dois geradores de 3V que estão em paralelo, o circuito fica com malha única e

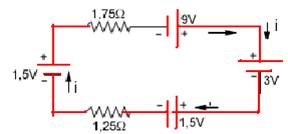
conforme a figura abaixo —i=((1,5+9) – (3+1,5))/(1,75 + 1,25)= 6/3 — i=2 A — R- D

14- Como eles estão associados em série, a tensão nos terminais das pilhas (U_g=4,5V) é igual à soma das tensões nos terminais da resistência R (U’) e do motor (U_m=4V) — 4,5=U’ + 4 — U’=0,5V — R=U’/i — 1=0,5/i — i=0,5 A — P_motor=i.U=0,5.4 — R- D

15- Receptor — figura 1 — reta ascendente — E’=5V — i=2 A – U=9V — U=E’ + r’.i — 9=5 + r’.2 — r’=2Ω — gerador — reta descendente — figura 2 — E=10V — i_cc=E/r — 20=10/r — r=0,5Ω — i=(10 – 5)/((0,5 + 2) — i=5/2,5 — i=2 A

R- A

16- I — receptor — E’=20V — i=5A – U=40V — U=E’ + r’.i — 40=20 + r’.5 — r’=4Ω — II — resistor — R=U/i=40/5 — R=8Ω — III — gerador — E=40V — i=5A — i_cc=E/r — 5=40/r —

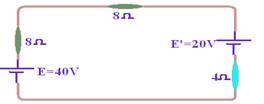
r=8Ω — montando o circuito — i=(40 – 20)/(8 + 8 + 4) —i=20/20 — i=1A — R- A

17- Equação do gerador — U=E – r.i — U_g=40 – 8i (I) — equação do receptor — U_r=E’ + r’.i —

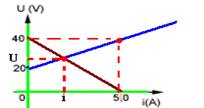
U=20 + 4.i (II) — na intersecção — U_g=U_r — substituindo (I) em (II) — 40 – 8i=20 + 4i — 20=12i — i=20/12 — i=5/3 A — U=20 + 4.5/3 — U=80/3V — R- C

18-

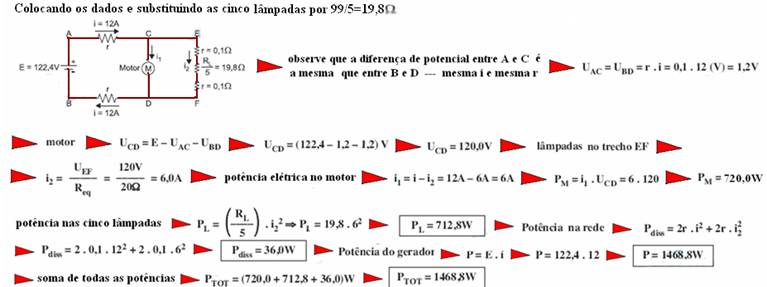
19- Gerador — reta descendente — E=100V — i=4 A — U=20V — equação do gerador — U=E – r.i — 20=100 – r.4 — r=20Ω — receptor — E’=40V — i=2 A — U=60V — equação do receptor — U=E’ + r’.i — 60=40 + r’.2 — r’=10Ω — cálculo da corrente i pela lei de Pouillet — i=(100 – 40)/(20 + 10) — i=2 A — observe que para essa corrente U é comum ao gerador e ao receptor — rendimento do gerador — η=U/E=60/100 — η_gerador=0,6=60% — η_receptor=E’/U=40/60 — η_receptor=0,67=67%

20- a) O circuito está esquematizado abaixo onde estão indicados os sentidos de percurso e da

corrente — + 11 + 0,1i + 0,1i – 12=0 — i=1/0,2 — i=5 A

b) Pela parte superior — V_A – V_B=+ 12 – 0,10.5 — V_A – V_B=11,5V — ou pela parte inferior — V_A – V_B=+ 11 + 0,10.5 — V_A – V_B=11,5V

21- Observe o esquema abaixo — figura a — U=2V — R_eq=R/2 — i’=i/2 — i=2i’ — R_eq=U/i — R/2=2V/i — i=4V/R — 2i’=4V/R — i’=2V/R — figura b — U=V — R_eq=2R — R_eq=U/i’’ — 2R=V/i’’ — i’’=V/2R — i’/i’’=2V/R x 2R/V — I’/i’’=4 — R- E

22- a) O gráfico 1 refere-se a um gerador e, portanto, representa a bateria — o gráfico 2 representa um receptor e, portanto, é o ventilador — gráfico 3 representa um resistor e, portanto, é o chuveiro.

b) O rendimento do receptor, ou seja, do ventilador — U = 10 + 2i — para i = 2 A — U = 14 V — rendimento — η = 10/14 — η = 71,4%

23- Equação do receptor — U=E’+ r’.i — 100=E’ + 2.5 — E’=90V — P=U.i=100.5 — P=500W — R- C

24- R- E — veja teoria

25- 01. Correta — se i=0, ou seja, se o gerador estiver em circuito aberto, tem-se:

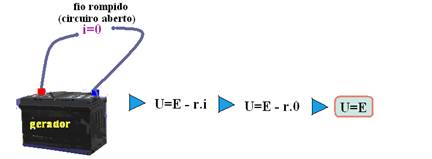
02. Correta — se o gerador estiver ligado a uma associação de resistores de resistência equivalente R_eq a potência máxima fornecida à essa

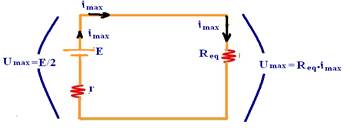
associação será — U_máx=Req.i_máx — E/2=R_eq.(E/2r) — r=R_eq

04. Falsa — veja teoria

08. Falsa — o rendimento elétrico de um receptor é definido pela razão entre sua potência útil e sua potência consumida — η=P_u/P_c — η=E.i/U.i — η=E/U
16- Correta — veja teoria
R- (01 + 02 + 16)=19

26-

27- 01. Percorrendo i circuito no sentido horário e supondo a corrente também no sentido horário — i – 15 + 3i + 4i + 5 + i + i=0 — i=1 A — Falsa

02- V_D – V_C=3.1=3V — V_D – V_C=3V — V_D > V_C — Falsa

04. U=E – ri=15 – 1.1 — U=14V — P=i.u=1.14 — P=14W — Verdadeira

08. P=R.i²=4.1² — P=4W — Falsa

R- 4

28- Potências de um receptor:

Potência total (Pt) – corresponde à energia total recebida pelo receptor da fonte externa (gerador) por unidade de tempo:

Potência dissipada (Pd) – refere-se à potência consumida (perdida, dissipada, sob forma térmica) pela resistência interna r’ do receptor e fornecida por:

Potência útil (Pu) –potência aproveitada pelo receptor para seu funcionamento normal, sob forma não térmica.Exemplo: num ventilador é a parcela da energia total que é transformada em energia exclusivamente mecânica.

Rendimento (η) de um receptor – definido como sendo a razão entre sua potência útil (Pu) e sua potência total Pt):

P_u=E’.i — 2000=E’.10 — E’= 200V — P_t=U.i=220.10=2200W — P_t=P_u + P_d — 2200=2000 + r’.i² — 200=r’.100 — r’=2Ω — η=P_u/P_t=2000/2200 — 0,909 — R- B.

29- O processo de resolução está explicado em fisicaevestibular.com.br (eletricidade-eletrodinâmica-circuitos compostos)

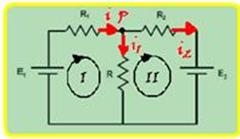
(I) partindo de P e percorrendo a malha no sentido horário — 1.i₁ – 14 + 1i=0 — i₁ + i = 14 (a) — (II) partindo de P e percorrendo a malha no sentido horário — 3i₂ + 14 – i₁=0 — 3i₂ – i₁ = -14 (b) — i=i₁ + i₂ (c) — resolvendo o sistema formado por (a), (b) e (c) — i₂=-2 A (sentido correto-anti-horário) — i₁=8 A sentido correto-horário) —

i=6 A (sentido correto-horário) — P_R2=R₂.i₂²=3.4=12W — R- E.

Receptores – Associação de geradores com receptores – Lei de Pouillet – Resolução

Voltar para os exercícios