Energia elétrica – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Potência elétrica – Energia elétrica
01- a) A lâmpada de menor potência – 40W
b) O de maior potência – caminhão
c) Lâmpada de 40W, lâmpada de 100W, ferro elétrico, fusca e caminhão
02- Quanto maior o número de equipamentos elétricos, maior o consumo de energia (III) — observe na expressão W=Po.Δt que o consumo de energia W depende também da potência do equipamento Po (I) e do tempo Δt de funcionamento (II) — R- E
03- Observe que em cada uma das recomendações você tentando diminuir o efeito Joule, ou seja, a transformação de energia elétrica em térmica — R- C
04- A energia elétrica é expressa por W=Po.Δt, medida em megawatts.hora MW.h) e não megawatts por hora (MW/h) — R- D
05- a) O disjuntor desliga quando a potência total for superior a Pot=i.U=15.110 — Pot=1.650W — o ferro elétrico e a lâmpada.
b) n=1.650W/100W — n=16,5 — n=16 lâmpadas
06- Po=i.U=0,2.10 — Po=2,0W
07- Po=i.U=2.600 — Po=1.200W — Po=W/Δt — 1.200=W/3.10-3 — W=3,6J — R- C
08- Po1=i1.U1=i1.110 — Po2=i2.U2=i2.110 — Po1=Po2 — 110.i1=220.i2 —i1=2i2 — a corrente que percorre o primeiro é 2 vezes maior que a corrente que percorre o segundo, mas o consumo de energia é o mesmo, pois a potência é a mesma — R- B
09- R- E — veja teoria
10- a) TENSÃO DE ALIMENTAÇÃO; 24V
POTÊNCIA CONSUMIDA: 150W
b) Po=i.U — 150=i.24 — i=6,25A
11- W=Po.Δt=30(1,5.8 + 3,3.1/3 + 0,2.10 + 0,36.10 + 0,1.6)=30.(12 + 1,1 + 2,0 + 3,5 + 0,6)=30.(19,4) — W=582Wh — regra de três — 1kWh – 0,40 — 1.362kWh – x — x=232,8 — R- E
12- a) Pot=4.000×60 + 600×200 — Pot=240.000 + 120.000 — Pot=360.000W — Pot=i.U — 360.000=120.i — i=3.000A
b) Wt=Pot.Δt=360.000×120=43.200.000Wh=43.200kWh — R$=43.200×0,40 — R$=17.280,00
13- W=Po.Δt=12.8800 — W=105.600Wh — W=105,6kWh — R$=105,6.0,5=52,80 — R- D
14- Po=i.U=2.105.2,5.107 — Po=5,0.1012W — W=Po.Δt=5.1012.10-3 — W=5.109J — regra de três — 1kWh – 3,6.106J — xkWh – 5,0.109J — x=5.109/3,6.106=1,39.103 — W=1.390kWh — C$=0,38.1390 — R$=530,00 — R- C
15- a) Cálculo da carga elétrica total Q pela soma das áreas dos 4 retângulos do gráfico acima — Q=(10.100 + 20.100 + 30.100 + 10.100) — Q=7.000A.min=7.000.60 — Q=420.000C — W=Q.U-420.000.120 — W=50.400.000J —
regra de três — 1kWh – 3,6.106J — xkWh – 50,4.106J — x=W=14kWh — custo=14.0,20 — C$2,80
b) Observe no gráfico que nos primeiros 42 minutos a corrente é de 10ª — Po=i.U=10.120 — Po=1.200W — W=Po.Δt=1.200.(42.60) — W=3.024.000J — apenas 1/3 dessa energia foi utilizada para aquecer a água — Wcalor=3.024.000/3 — Wcalor=1.008.000J — equação fundamental da calorimetria — Wcalor=m.c.Δθ — 1.008.000=10.4,2.103. Δθ — Δθ=1.008.103/42.103 — Δθ=24oC
16- Cálculo da corrente na lâmpada — Pl=i.U — 6=i.12 — i=0,5A (C/s) — carga na bateria — Q=45/2A.h=22,5.3.600 — Q=81.000C — i=Q/Δt — 0,5=81.000/Δt — Δt=162.000s=162.000/3.600 — Δt=45h — R- C
17- Campo Grande — anual — P0=700W — área 1m2 — Δt=365diasx6h — Δt=2.190h — Po=W/Δt — 700W=W/2.190h — W=2.190.700=1.533.000W.h — WCampo Grande=1.533kWh — energia coletada em Campo Grande, por m2 de área durante um ano, 6h ao dia — equipamento de captação — We=1.533kWh x 0,6(60%) x 4(área de captação 4 vezes maior) — We=3.679,2kWh — economiza 3.679,2 x 0,60 — C$=2.207,00 — R- A
18- Televisão de 29 polegadas — Po=W/Δt — 70=W/6.30 — W=12.600Wh=12,6kWh — televisão de 42 polegadas — Po=W/Δt — 220=W/180 — W=39.600Wh=39,6kWh — diferença — Wd=39,6 – 12,6 — Wd=27kWh — R- B
19- Decodificador — Wd=Pod.Δt=6.30,24 — Wd=4.320W.h — lâmpada — Wl=Pol.Δt — Wl=Wd=4.320=60.Δt —
Δt=4.320/60 — Δt=72h — R- E
20- no Equador — We=792.106J — aquecedor — Wa=Po.Δt=i.U.Δt=20.220. Δt=4.400.Δt — We=Wa — 792.106=4.400.Δt — Δt=792.106/44.102 — Δt=180.000s/3.300=50h — R- C
21- a) V=λf — 3.108=λ830.106 — λ=0,36m
b) Q=0,8Ah=0,8C/s.1h=0,8C/s.3600s — Q=2.880C
c) i=Q/Δt=2.880/110.60 — i=0,44 A — W=Q.U=2.880.6 — W=17.280J — Po=W/Δt=17.280/110.60=17.280/6.600 — Po=2,62W
22- Comparando, em termos de porcentagem, 60lm/W com 15lm/W, você verifica que, ao substituir uma lâmpada de 15lm/W por outra de 60lm/W, o rendimento será de 75% — como cada lâmpada tem 100W e são 10 lâmpadas, a economia de potência será P =10.0,75.100= 750 W, que fornece, em um mês (30 dias), uma economia de energia (W) que,funcionando 6h por dia — W=Po.Δt=750.30.6 — W=135.000Wh — W=135kWh — economia=135.0,30 —
C$=40,50 — R- C
23- W=Po.Δt=200.60 — W=12.000J — 1cal – 4J — Qcal – 12.000J — 4Q=12.000 — Q=3.000cal — Q=m.c.Δθ —
3.000=100.1. .Δθ — .Δθ=30oC — R- E
24- Decodificador — Wd=Pod.Δt=6.30,24 — Wd=4.320W.h — lâmpada — Wl=Pol.Δt — Wl=Wd=4.320=60.Δt —
Δt=4.320/60 — Δt=72h — R- E
25- a)Energia de Itaipu — WI=87.600GWh=87.600.109Wh — energia captada pela área S em 1 ano — WS=0,2.Po.Δt — WS=0,2.170.W/m2.S.360.24=293.760S — WS=WI — 293.760S=87.600.109 — S=87.600.109/293.760 — S=0,3.109 — S=3.108m2 — S=3.108.10-6 — S=3.102km2
b) Porcentual médio — P=87.600.109Wh/14.000.106.24.360=87.600.109/14.24.360.109 — P=0,724 — P=72,4%
26- Comparando, em termos de porcentagem, 60lm/W com 15lm/W, você verifica que, ao substituir uma lâmpada de 15lm/W por outra de 60lm/W, o rendimento será de 75% — como cada lâmpada tem 100W e são 10 lâmpadas, a economia de potência será P =10.0,75.100= 750 W, que fornece, em um mês (30 dias), uma economia de energia (W) que,funcionando 6h por dia — W=Po.Δt=750.30.6 — W=135.000Wh — W=135kWh — economia=135.0,30 —
C$=40,50 — R- C
27- Po=i.U=400.12 — Po=4.800W — R- C
28- Gráfico que fornece a quantidade de energia na forma de luz visível pode ser calculado como sendo aproximadamente a
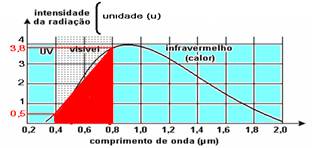
área do trapézio da figura — S1=(B + b).h/2=(3,8 + 0,5).0,4/2 — S1=0,86 — S2 – área do gráfico que
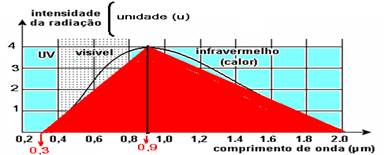
fornece quantidade total de energia gasta para o funcionamento da lâmpada – área do triângulo — S2=b.h/2=1,7.4/2 — S2=3,4 — eficiência — e=S1/S2=0,86/3,4=0,252 x 100=25,2% — R- C
29- Excluindo as lâmpadas, em cada cômodo da casa existe um aparelho elétrico citado na primeira tabela — soma de suas potências — P1=120 + 3.000 + 500 + 200 + 200 + 50=4.070 — P1=4.070W — cada lâmpada — na sala – área=3.3=9m2 – 100W — no banheiro – área=1,5 x 2,1=3,1m2 – 60W — no corredor – área=0,9 x 1,5=1,3m2 – 60W — no quarto – área=2,8 x 3=8,4m2 – 100W — potência das lâmpadas – Pl=100 + 60 + 60 + 100=320W — potência total instalada na casa — Pt=P1 + Pl=4.070 + 320 — Pt=4.390W — R- D
30- Energia elétrica consumida em um mês funcionando 10h por dia — W=Po.Δt=180.30.10=54.000Wh=54kWh — regra de três — 54kWh – 50% — x – 100% — x=54.100/25=216kWh — R- E
31- As lâmpadas fluorescentes produzem maior luminosidade utilizando a mesma potência e materiais com melhores características condutoras reduzem a perda de energia por calor (efeito Joule) — R- E
32- U=1,1V — m=63,5μg=63,5.10-6g — Δt=193s
![]()
Po=i.U=1,0.10-3.1,1=1,1.10-3W=1,1mW — R- A
33- Cálculo da corrente elétrica fornecida pela bateria — P=iU — 60=i.12 — i=5 A — a carga Q fornecida permanecerá a mesma, fornecendo 5 A de corrente durante — i=Q/Δt — 5= 60/Δt — Δt=60/5 — Δt=12h — R- C
34- R- A — veja teoria
35-
![]()
36- a) P=iU — 7.200=i.120 — i=60 A
b) Wtotal=4kW.2h + 6kW.2h + 2kW.2h — Wtotal=24kWh
c) W=24.30=720kWh — preço — p=720.0,5 — p=R$ 360,00
37- Aplicando a 1ª Lei de Ohm a esse resistor, temos — U = R I — 120 = R (8) — R = 15 Ω — P=U2/R=1502/15 P=1.500W
R- B
38- Dados: P = 4.500 W — U = 110 V.
P = i U — i = P/U=4.500/110=40,9 A — portanto o disjuntor escolhido deverá ser o de 45 A, que é o valor mais próximo do acima do calculado — R- C
39- Sendo N a quantidade de dispositivos, P a potência elétrica e Δt, o tempo efetivo de uso diário, e C (R$ 0,50) o custo do kWh, o gasto diário dos dispositivos é — G = N x P x Δt x C — aplicando essa expressão, você obtém a tabela
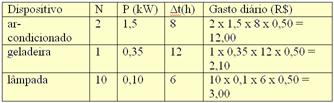
— gasto mensal (30 dias) — Gmensal = 30.( 12,00 + 2,10 + 3,00) = 30 (17,10) — Gmensal = R$ 513,00 —
R- B
40- Dados — V = 120 L — m = 120 kg — ΔT = 30°C — c = 1 cal.g-1.°C-1 = 4.200 J.kg-1.°C-1 — quantidade de calor gasta diariamente — Q = m c ΔT = 120 x 4.200 x 30 = 15,12.106 J — equivalência entre quilowatt hora e joule —
1 kWh = (103 W) x (3.600 s) = 3,6 x 1066W.s = 3,6 x 106 J — regra de três — 3,6.106J – 1 kWh — 15,12.106J – Q — Q=15,12.106/3,6.106 — Q=4,2kWh — gasto total com esse dispositivo em 30 dias — Gtotal = 30 x 4,2 x 0,50 — Gtotal = R$ 63,00 — R- B
41- Po=i.U=2.10-6.5.104=10.10-2 — Po=0,1W — R- A
42- Δt=45/60hx30 — Δt=22,5h — Po=W/Δt — 5.000=W/22,5 — W=11.250Wh=11,25kWh — gasto — g=11,25×0,20=22,40
R- C
43- Recebe – Por=50J/s — libera – Pol=20J/s — ganha continuamente Pog=(50 – 20)=30J/s — ao atingira 1.000J ele derrete e para que isso ocorra ele deve receber W=(1.000 – 550)=450J de energia — Po=W/t — 30=450/t — t=15s
R- D
44- Po1=W1 /Δt — 5.000=W1/Δt — Δt=W1/5.000 (I) — Po2=W2/Δt — 4.000=W2/Δt — Δt=W2/4.000 (II) — igualando I com II — W1/5.000=W2/4.000 — W2=0,8W1 — o novo chuveiro utiliza 80% da potência do anterior e economiza 20% — economizará — 0,2×40=8,00 — R- B
45- O relógio indicou um consumo de 2.563 kwh no mês anterior e de 2.783 kwh na última leitura — a diferença entre essas duas medidas determina um consumo de 220 kwh no período de um mês — regra de três — 1 kwh – R$ 0,20 — 220 kwh – C — C=0,20×220 — C= R$ 44,00 — R- E
46- A tensão alternada produzida pelos geradores na usina hidrelétrica é relativamente baixa. Assim, para que se possa abastecer diferentes centros utilizando linhas de transmissão, essa tensão é aumentada até centenas ou milhares de kV por meio de transformadores. Ao atingir os centros de consumo, a tensão é reduzida, por exemplo, a algumas dezenas de kV, pelos transformadores das subestações e distribuída para o público. A tensão de transmissão é elevada e a corrente diminuída porque assim se podem utilizar fios condutores mais finos (mais leves, mais baratos) já que, para que a potência seja a mesma (P=Ui) se você aumentar a tensão (U) você deve diminuir a corrente i.
R- E
47– Po=U.i=ε.i=12.100=1.300W — Po=W/Δt — 1.200=W/60 — W=1.200×60=7.200W — W=7,2.104W — R- D
48–

R- A
49-(UFPA-PA)
Po=W/∆t — W=Po.∆t — lâmpadas — W1=0,1.10=1kWh — televisão — W2=0,1.8=0,8kWh — geladeira — W3=0,3.24=7,2kWh — ventilador — W4=0,125.8=1,0kWh — Wtotal=1,0 + 0,8 + 7,2 + 1,0=10,0kWh — 1 painel – 0,5kWh — n painéis – 10,0kWh — N=20 painéis — R- D
50-(ENEM-MEC)
– Os biocombustiveis de primeira geração são produzidos a partir da fermentação alcoólica dos açúcares vegetais da biomassa que contenha amido ou sacarose, como por exemplo o milho, o trigo, o sorgo, o amendoim, a soja, a beterraba, a batata doce, o girassol e a cana-de-açúcar, não utilizando a celulose — porém, para evitar que se atinja o limite da oferta ou venha a ocorrer a competição pelo uso da terra para a produção de biocombustíveis e de alimentos, é necessário investir no desenvolvimento de tecnologias de segunda geração para produção de etanol com o aproveitamento eficiente da celulose — estimativa é de que o aproveitamento do bagaço e parte das palhas e pontas da cana-de-açúcar eleve a produção de álcool em 30% a 40%, para uma mesma área plantada — demais matérias-primas para as quais se buscam tecnologias de processamento da celulose, tais como capim-elefante, braquiárias, panicuns e árvores de crescimento rápido podem representar alternativas competitivas e eficientes para locais onde não se cultiva ou cultivará cana-de-açúcar, podendo gerar novos empregos — R- A.
Voltar para os exercícios
