Wheatstone Bridge EN
WHEATSTONE BRIDGE
Galvanometer as Ammeter and as Voltmeter – Wheatstone Bridge
Galvanometer
The galvanometer is a device that measures low-intensity currents and is composed, in a very simple way, of many straight conductors running an electric current, the same principle used in the construction of electric motors.
Symbol of a galvanometer
Galvanometer adapted for ammeter
When you want the galvanometer to measure currents greater than its full scale (functioning as an ammeter) you must associate, in parallel to it, a resistor (R S ) called a shunt (in English, deviation).
The whole set , galvanometer with resistance R G and the shunt resistance parallel to it constitutes the ammeter, which becomes a large-scale galvanometer.
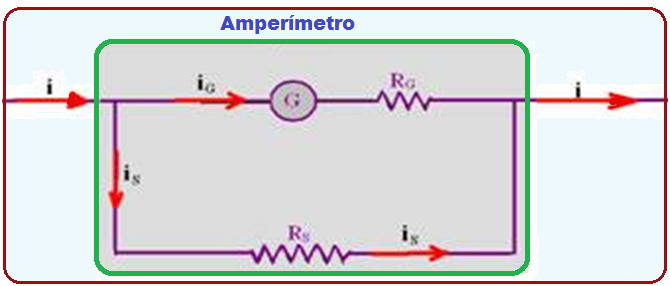
i 
full scale total current you want to measure
i G full-scale current of the galvanometer
i S current that is shunted to the shunt resistance (R S )
R G internal resistance of galvanometer
Carefully analyze this numerical example :
You have a galvanometer with internal resistance R G = 100 Ω and full-scale current i G = 10 mA.
To measure currents up to i = 1 A (when the full-scale current of the galvanometer is marking 10 mA , it should actually be marking 1 A ), you must transform it into an ammeter, placing a resistance of (100/99) Ω in parallel.
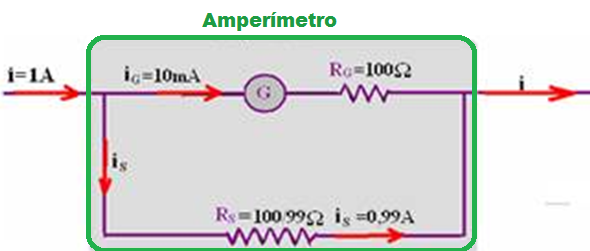
Thus, the current that makes the galvanometer pointer go to the full scale is i = 1A when 0.01 A is passing through the galvanometer and the part that diverts to the shunt is i S = 0.99 A.
Thus, if the galvanometer were marking 5 mA (half of the scale), in reality the measured current would be 0.5 A (half of 1 A).
Note that the multiplication factor is n = (1 + R G /R S )= 1 + 100/(100/99 ) =100 n = 100 (when it should mark 0.01 A it will be marking 100×0.01 = 1 A ).
Galvanometer adapted for voltmeter
When you want the galvanometer to measure voltages (voltages or ddps) greater than its full scale, you must associate, in series with it, a resistance (R M ) called a multiplier resistance.
The entire set, galvanometer with resistance R G and the multiplier resistance in series with it constitutes the voltmeter , which becomes a large-scale galvanometer.
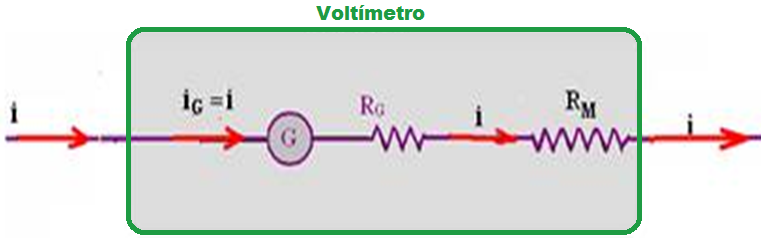
Note that the current i is the same in both the galvanometer and the multiplier resistance R M and that the total voltage (U) which is the full-scale voltage indicated by the voltmeter is the sum of the full-scale voltage in the galvanometer (U G ) and the voltage in the multiplier resistance (U M ).
U = U G + U M U M = R M .i U G = R G .i i = U G /R G U = U G + R M .U G /R G U = U G ( 1 + R M /R G ) U = mU G the expression m = (1 + R M /R G ) is called the multiplication factor.
Carefully analyze this numerical example :
You have a galvanometer with internal resistance R G = 100Ω and full-scale current i G = 10mA.
To measure voltages up to 3V (when the full-scale current of the galvanometer is marking 10mA, it will actually be marking 3V ), you must connect a 200Ω multiplier resistance in series so that it becomes a voltmeter that indicates between 0 and 3V — proving U=R G .i + R M.i =100.0.01 + 200.0.01 U=3V.
Wheatstone Bridge
It is a combination of three fixed resistors and one variable resistor (rheostat), as shown in the figure.
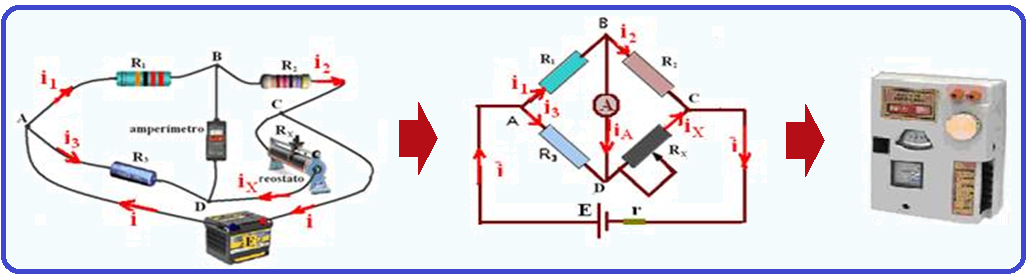
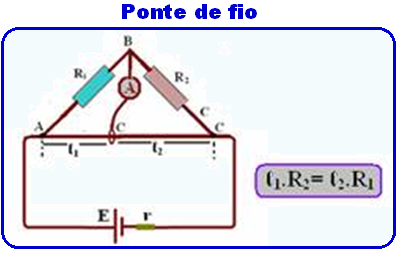
It serves, among other things , to determine the resistance of a resistor. Knowing, for example, R 1 , R 2 and R 4 , one can determine R 3 , as follows:
A very sensitive ammeter (galvanometer) is connected between B and D.
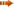The rheostat (variable resistance) R X is varied until the current intensity i A in the ammeter becomes zero (i A = 0).
In this situation, the bridge is said to be in equilibrium . Since the current in the ammeter is zero, there is no potential difference between points B and D.
Wire bridge
What you should know, information and tips
If the bridge is in balance, that is, if R 1 . R X = R 2 . R 3 , you can touch points B and D with your hands and not get a shock and also any electrical device placed between B and D will not work, since V B = V D and no electrical current passes through this section.
