Associação de geradores – Resolução

Resolução comentada dos exercícios de vestibulares sobre

Geradores – Associação de geradores

 

01- R- D  —  veja teoria

02- Quando i=50 A  —  P=0,6kW=600W  —  P=E.i —  600=E.50  —  E=12V   

03– R- C  —  veja teoria

04– Veja a figura abaixo

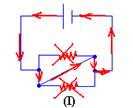
R-  A

05– Do gráfico  —  E=12V  —  i_cc=E/r  —  4=12/r  —  r=3 Ω  —  R- C

06- E=12V  —  i_cc=E/r  —  4=12/r  —  r=3Ω  —  R- D

07- R- A  —  veja teoria

08- E=10V  —  pelo gráfico  —  i=2A  —  U=9V  —  U=E – r.i  —  9=10 – r.2  —  r=0,5Ω  —   R_eq=0,5 + 3,5=4,0Ω  —  R_eq=U/i=E/i 

—  4=10/i  —  i=2,5A  —  R- A

09- O tamanho da pilha ou da bateria está diretamente relacionado com a intensidade de corrente elétrica que ela deve

fornecer a um circuito  —  R- E

10– i=Q/Δt  —  Q=i.Δt=30A.1h  —  Q=30Ah  —  Q=30A.3.600s  —  Q=108.000C  — Q=108kC  —  W=Q.U  —  W=108.000.12  —  W=1.296.000J=(W.s)  —  W=1.296.000/3.600=360Wh  —  W=0,36kWh  —  R- C

11– E=1V (circuito em aberto)  —  i_cc=E/r  —  20A=1/r  —  r=0,05Ω

12– a) Do gráfico  —  fem  —  é a tensão U quando i=0  —  U=E – r.i  —  U=E – r.0  —  U= E=15V  — corrente de curto circuito  —  ocorre quando U=0  —  U=E – r.i  —  0=E – r.i_cc  —   i_cc=E/r  —  60=15/r  —  r=0,25Ω

b) P_t= P_d + P_u  —  P_u=P_t – P_d  —  P_u=E.i – r.i²  —  esta expressão fornece o gráfico abaixo, com suas principais características  — 

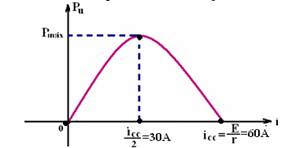
P_máx=E.i_máx – r.i_máx²=15.30 – 0,25.(30)²=450 – 225  —  P_máx=225W

13– a) Quando P_máx=50A, i_máx=5A  —  P_máx=U_máx.i_max  —  50=U_máx.5  —  U_máx=10V  —  U_máx=E – r.i_máx  —  10=E – r.5  —

r=(E – 10)/5  —  i_cc=E/r  —  10=E/(E – 10)/5  —  5E=100  —  E=20V  —  verdadeira

b) Correta  —  veja teoria

c) i_cc=E/r  —  10=20/r  —  r=2Ω  —  verdadeira

d) correta  —  quando P é máxima  —  R_eq=r=2Ω

e) Falsa  —  a potência é máxima quando i=5A
R-= E

14- P_máx=E.i  — 300=E.20  —  E=15V

15- Corrente elétrica que ela fornece ao circuito externo  —  P_u=U.i  —  1,8=3,6.i  —  i=0,5A  —  i=Q/Δt  —  0,5 A=0,6 A.h/Δt  —  Δt=0,6A.h/0,5A  —  Δt=1,2h  —  R- B

16- Como no gerador a corrente elétrica entra pelo pólo negativo e sai pelo positivo, sobram as alternativas a), b) e e)  —   a maior transferência ocorre com a alternativa que fornecer maior potência útil  —  a) U_a= E – r.i=15 – 0.1=15V – P_a=U.i=15.1=15W  — 

b) U_b=E – r.i=12 – 0.1=12V  — P_b=U.i=12.1=12W  —  e) U_e=E – r.i=10 – 1.2=8V  —  P_e=U.i=8.2=16W  —  R- E

17- I- Correta  —

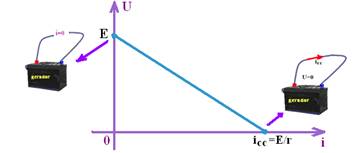
II- Quando r.i=E  —  U=E – r.i  —U=E – E  —  U=0  —  ele não submete nenhuma d.d.p. ao circuito externo  —  se U=0  —  i=0  —  correta

III- Correta  —  real tem resistência externa, ou seja, tem r.i  —  U=E – r.i=E – U’  —  U é menor que E.

R- E

18- Situação II  —  U=E – r.i  —  V_A=ε – R_o.i_gerador  —  V_o= ε  —  situação II  —  i_geradoe=i_lâmpada=i  —  na lâmpada  —  V_A=4.i  —  i=V_A/4=( ε/1,2)/4   —  i= ε/4,8  —  V_A= ε – R_o.i  —  ε/1,2= ε – R_o.(ε/4,8)  —  4=4,8 – R_o  —  R_o=0,8Ω  —  R- A

19- a) Do gráfico  —  E=1,5V  —  quando i=1A  —  U=1,2V  —  U=E – r.i  —  1,2=1,5 – r.1  —  r=0,3Ω

b) R_eq=0,3 + 1,7  —  R_eq=2Ω  —  R_eq=E/i  —  2=1,5/i  —  i=0,75A

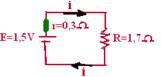
R- i=0,75A

20- Quando R=5,8Ω  —  U’=11,6V  —  R=U’/i’  —  5,8=11,6/i’  —  i’=11,6/5,8  —  i’=2A  —  quando R=3,8Ω  —  U’’=11,4V  —  R=U’’/i’’  —  3,8=11,4/i’’  —  i’’=3A  —  U’=E – r.i’  —  11,6=E – r.2 (I)  —  U’’=E – r.i’’  —  11,4=E – r.3 (II)  —  resolvendo I com II  —  r=0,2Ω e E=12V  —  acrescentando o resistor de 11,8Ω  —  R_eq=U/i=E/i  —  (11,8 + 0,2)=12/i  —  i=1 A  — potência elétrica dissipada no resistor de 11,8Ω  —  P=R.i² 11,8.(1)²  —  P=11,8W  —  energia dissipada em 10s  —  W=P.Δt=11,8.10  — W=118J

21– A transferência de energia será máxima quando r=50Ω=R_eq

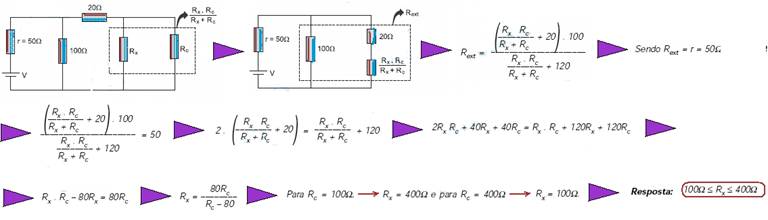
22-

23- R- B  —  observe que as pilhas estão associadas em oposição de fase.

24- R- B  —  veja teoria

25- Veja figuras abaixo:

 E_eq=5E  —  r_eq=5r  —  com R=10Ω e com i=5A  —  R_eq=U/i  —  10 + 5r=5E/5  —  5E=25r + 50 ( I )  —  com R=28Ω e com i=2A  —  R_eq=U/i  —  28 + 5r=5E/2  —  10r + 56=5E ( II )  —  igualando I com II  —  25r + 50=10r + 56  —  r=6/15  —  r=0,4Ω  —  E=12V  —  R- A

26- O tamanho da pilha ou da bateria está diretamente relacionado com a intensidade de corrente elétrica que ela deve

fornecer a um circuito  —  observe na figura acima que as lâmpadas possuem a mesma força eletromotriz e, assim, como a maior fornece maior corrente, consequentemente ela deve fornecer maior potência (P=U.i) e possuir menor resistência interna  —  R- E

27- Observe que as pilhas estão em paralelo e a ddp fornecida a R=30Ω é de E_eq=U=1,5V  —  R=U/i  —  30=1,5/i  —  i=0.05A   —   R- A

28- R- C  —   E_eq=6,0V

29– R- A  —  veja teoria

30- Cálculo da resistência da lâmpada  —  P=U²/R  —  9=12²/R  —  R=16Ω  —  corrente na lâmpada que está submetida à tensão fornecida pelas 4 pilhas em série e que é de E_eq=U=1,5.4=6V  —  R=U/i  —  16=6/i  —  i=0,375 A  —  P=R.i²=16.(0,375)²=16.0,140625  —  P=2,25W  —  R- E

31– Observe que estão em paralelo  —  E_eq=1,2V e r=1,2/3=0,4Ω  —  R- A

32– Quanto maior a corrente através de cada lâmpada, maior será seu brilho  —  resistência da lâmpada R  —  figura 1  — R=E/i₁  —  i₁=E/R  —  a) R_eq=3E/i_P  —  i_P=3E/2R=1,5E/R  —  b) R_eq=3E/i_Q  — i_Q=3E/3R=E/R  —  c) R_eq=2E/i_S  —  i_S=2R/2R=E/R  —  d) R_eq=2E/i_T  —  i_T=2E/3R/2=4E/3R=1,3E/R  —  R_eq=3E/i_’U—  i’_U=3E/(R/3)=9E/R  —  i_U=i’_U/3  —  i’_U=3i_U  — 

3i_U=9E/R  —  i_U=3E/R  —  maiores que E/R são P,T e U  —  R- C   

33– a) Duas pilhas estão em oposição de fase e sua força eletromotrizes se anulam  —  E_equ=1,5V  —  r_eq=3.r=3.2/3=2Ω  —  R_eq=U/i  —  2 + 3=1,5/i  —  i=1,5/5  —  i=0,3A

b) na lâmpada  —  P=R.i²=3.(0,3)²=3.0,09  —  P=0,27W

c) Pilha invertida  —  P=0,27W  —  pilhas corretas  —  R_eq=U/i’  —  2 + 3=4,5/i’  —  i’=0,9 A  —  P_o=R.(i’)²=3.(0,9)²  —  P_o=2,43W  —  F=P/P_o=0,27/2,43  —  F=1/9

34– Maior corrente i  —  maior brilho  —  i_L=E/R  —  i_P=3E/2R=1,5E/R  —  i_Q=3E/3R=E/R  —  i_R=E/2R=0,5E/R  —  i_S=2E/(3R/2)=4E/3R=1,3E/r  —  i_T=i_S/2=0,7E/R  —  i’_U=3E/(R/3)=9E/R  —  i_U=i’_U/3  —  i_U=3E/R  —  R- E

35-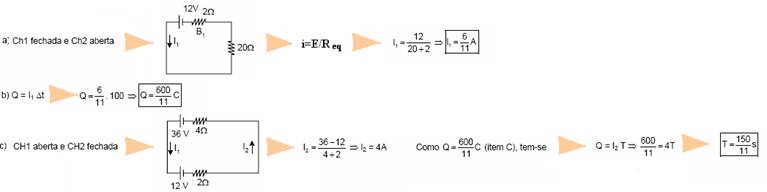 

36-

R- A

 

37– Como estão associadas em paralelo a diferença de potencial U é a mesma para cada ramo e para o aparelho e vale U=2V  — no aparelho  — R_eq=U/i  —  R=2V/i  —  i=2V/R  —  R- B

38- Cálculo do gerador equivalente  —  série  —  E_eq=5.000×0,15  —  E_eq=750V  —  r_eq=5.000×0,25  —  r_eq=1.250Ω  —  têm-se 140 geradores de E_eq=750V e r_eq=1.250Ω associados em

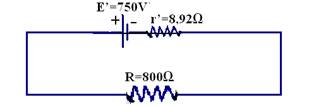
 paralelo onde a fem equivalente é E’=750V e a resistência interna equivalente é r’=1250/140  —  r’=8,92Ω  —  R_eq=U/i  —  (8,92 + 800)=750/i  —  i=750/808,92  —  i=0,927A  —  R- C

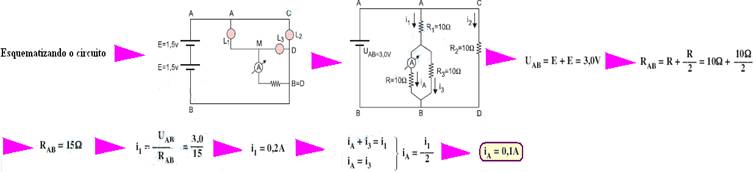
39- a) calculando a força eletromotriz e a resistência interna do gerador equivalente  —  as três pilhas em paralelo  —–  E’=1,5V e r’=0,3/3  —  r’=0,1Ω  —  essa pilha equivalente está em série

com a quarta pilha  —  E_eq=1,5 + 1,5  —  E_eq=3,0V  —  r_eq=0,1 + 0,3  —  r_eq=0,4Ω  —  R_eq=U/i  —  (0,4 + 13,6)=3/i  —  i=3/14  —  i=0,21A  —  P=R.i²=13,6.(0,21)²  —  P=0,6W

b) i_cc=E_eq/r_eq=3/0,4  —  i_cc=7,5A

40– Para que a lâmpada brilhe normalmente (dentro das especificações), a corrente i através dela deve ser de  —  P=i.U  —  6=18.i  —  i=1/3=0,33A  — resistência da lâmpada  —  P=U²/R  —  6=(18)²/R  —  R=54Ω  —   na seqüência abaixo está todo processo do cálculo do gerador equivalente  —  E_eq=18V  —  r_eq=0,55Ω  —  cálculo da corrente i’ no circuito  — R_eq=U/i’  —

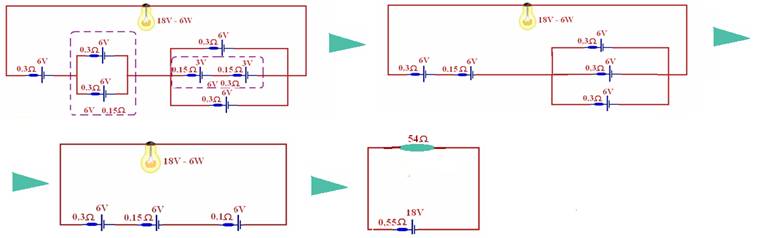
54 + 0,55=18/i’  —  i’=18/54,55  —  i’=0,33A  —  i=i’=0,33 A  —  a lâmpada brilhará normalmente

41- R- C  —  veja teoria

42- R- E  —  veja teoria

43- A bateria é um gerador eletroquímico. A bobina acoplada ao motor produz corrente alternada,

 que é, no alternador,transformada em corrente contínua, fornecendo energia para recarregar a bateria que, por sua vez, fornece energia para acender os faróis, alimentar o rádio, as lâmpadas do painel etc. 

R- E

44- R- D  —  veja teoria

 

45- Curva característica do gerador – é representada por um gráfico que relaciona a intensidade de corrente elétrica i no gerador com a diferença de potencial (tensão) U em seus terminais.

 Se i=0, ou seja, se o gerador estiver em                         Se U=0, ou seja, se o gerador estiver em curto circuito, tem-se

circuito aberto, tem-se:

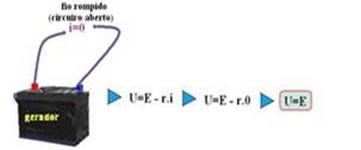
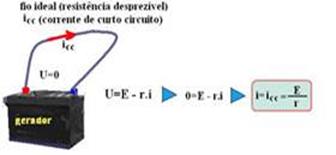
 Os pares de valores U=E e icc=E/r determinam dois pontos no gráfico Uxi, que unidos por um segmento de reta (função do primeiro grau) fornece a curva característica de um gerador  —  como as grandezas são proporcionais, completando o gráfico  —  i_cc=24 A  —  E=12V 

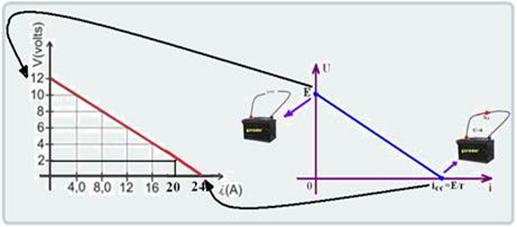
i_cc=24 A  —  E=12V —  i_cc=E/r  —  24= 12/r  —  r=0,5Ω  —  R- C

46-

 a) Período da roda (tempo que ela demora para efetuar uma volta completa)  —  T_R=0,5s  —  velocidade angular da roda de raio R=50cm=0,5m  —  W_R=2.π/T_R=2.3/0,5  —  W_R=12 rad/s  —  como a roda de raio R=50 cm e o dínamo de raio r=0,8 cm estão acoplados, todos os pontos da superfície externa de cada uma tem a mesma velocidade linear (escalar)  —  V_R = V_D­  —  W_R.R = W_D.r  —  12.0,5 =

W_D.0,8   —  W_D= 750rad/s. 

b) período T_D do dínamo  —  W_D=2.π/T_D  —  750=2.3/T_D  —  T_D=8,0.10^-3s

c) Cálculo da força eletromotriz ε =U  —  P=U²/R  —  24=ε²/6  —  ε=12V.

47- Para você acender a lâmpada ela deve ser submetida a uma diferença de potencial (tensão, voltagem) e, consequentemente percorrida por corrente elétrica  —  os dois polos da lâmpada são a

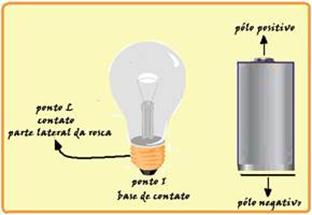
parte inferior da rosca (ponto I) e a parte lateral da lâmpada (ponto L)  —  os dois pólos da pilha estão indicados na figura  —  para que a lâmpada acenda o ponto L deve estar ligados a um dos polos da pilha e o ponto I da lâmpada ao outro pólo da pilha, o que ocorre nas situações 1, 3 e 7  —  R- D.

Voltar para os exercícios