Capacitores – Resolução
Resolução comentada dos exercícios de vestibulares sobre
Capacitores
01- C=Q/U — como a capacitância C é constante para cada capacitor — se dobrar Q, U também deverá dobrar — R- C
02- Como as pilhas estão associadas em série — E=U=1,5 + 1,5 — U=3,0V — C=Q/U — 6,0.10-5=Q/3,0 — Q=18.10-5C — Q=1,8.10-4C — R- D
03- C=Q/U — 10-3.10-3=Q/102 — Q=10-6.102 — Q=10-4=10-1.10-3=0,1.10-3C — Q=0,1μC — R- C
04- Energia liberada pelo capacitor ao se descarregar — W=C.U2/2=22.10-3.(25)2/2 — W=6,875J — essa energia foi utilizada para elevar o tijolo de massa 0,5kg a uma altura h e vale — W=mgh — 6,875=0,5.10.h — h=6,875/5 — h=1,375m — R- C
05- Como a capacitância C é uma constante característica de cada capacitor, as variações entre Q e U são proporcionais — C=ΔQ/ΔU — C=6.10-5/(60 – 50) — C=6.10-6F — R- C
06- energia armazenada — W=C.U2/2=1,2.10-6.(3.103)2/2 — W=1,2.10-6.9.106 /2 — W=5,4J — R- B
07- A capacitância é constante e vale — C=Q/U=60.10-6/3=180.10-6/9 — C=20μF — quando U=20V — C=Q/U — 20.10-6 = Q/20 — Q=400μC
08- Energia liberada pelo capacitor ao se descarregar — W=C.U2/2=10-2.(16)2/2 — W=1,28J — essa energia é utilizada para elevar o bloco de h — W=m.g.h — 1,28=0,10.10.h — h=1,28m —
R- C
09- O televisor deixa de funcionar no início dos 5 minutos quando a tensão é de 80V — a capacidade é constante e vale — C=Q/U=10/1.000 — C=10-2F — C=Q/U — 10-2=Q/80 — Q=80.
10-2 — Q=0,8C — R- D
10- R- D — veja teoria
11- C= Q/U — 8,85.10-12=Q/102 — Q=8,85.10-10C — R- A
12- C= Kεo.A/d — como o dielétrico é o ar — K=1 — A=200cm2=2.102.10-4=2.10-2m2 — C= Kεo.A/d — 8,85.10-12= 1.8,85.10-12.2.10-2/d — d=2.10-2m — R- E
13- dobrando a área, a capacitância C também dobra — dobrando d, a capacitância C fica reduzida à metade — R- A
14- a) C=Q/U — 40.10-6=Q/40 — Q=1.600.10-6 — Q=1,6.10-3C
b) W=C.U2/2=40.10-6.(40)2/2 — W=3,2.10-2J
c) dobrando d, a capacitância C cai pela metade — C=40μF/2 — C=20μF
15- a) d=150m — E=3.106V/m — U=E.d=3.106.150 — U=450.106V — C=Q/U — 1,6.10-8=Q/450.106 — Q=720.10-2 — Q=7,2C
b) energia fornecida pela descarga — W=C.U2/2=1,6.10-8.(450.106)2/2 — W=1,62.109J — P=W/Δt=1,62.109/3.600 — P=45.104W — 1 lâmpada – 60W — n lâmpadas – 45.104W — n=45.104/60=0,75.104 — n=7.500 lâmpadas
16- a) i=Q/Δt — 50.103=Q/10-3 — Q=50C
b) C= εo.A/d=9.10-12.200.106/2.103 — C=9,0.10-7F
c) C=Q/U — 9.10-7=50/U — U=50/9.107 — U=5,6.107V
17- 
R- B
18- Quanto mais dielétrico, maior será C e consequentemente maior U e maior Q, pois como C é constante, Q e U são diretamente proporcionais — R- C
19- 1. Verdadeira — o potencial da placa A (positiva) é maior que o da placa B (negativa).
2. Falsa — o sentido do campo elétrico no interior das placas é das cargas positivas para as negativas.
3. Falsa — C=Q/U — 10-6=Q/100 — Q=10-4C=100μC
4. Verdadeira — cargas de mesmo sinal se repelem e cargas de sinais opostos se atraem.
5. Verdadeira — a capacitância é inversamente proporciona à distância entre as placas
6. Verdadeira — essa é a principal característica dos capacitores
R- 1.V; 2.F; 3.F; 4.V; 5.V; 6.V
20– a) Como a capacitância C é diretamente proporcional à constante dielétrica, C ficará também 5 vezes maior — C=Q/U — como Q é a mesma, para C ficar 5 vezes maior, U deverá ficar 5 vezes menor — U=200/5 — U=40V
b) U=8.105V — d=0,5mm=5.10-4m — U=E.d=8.105.5.10-4 — U=40.101 — U=400V
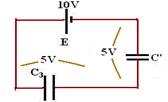
21- A ddp U é a mesma, pois a fonte é sempre a mesma — antes — E=U/d — E=12/d — depois — E’=12/2d — E’=E/2 — o campo elétrico cai pela metade — C=εA/d — Q.U= εA/d — Q= εA/d.U — observe nessa expressão que a única grandeza variável é d e que é inversamente proporcional a Q, ou seja, se d dobrar, Q ficará reduzida à metade — R- D
22- A capacitância C é diretamente proporcional à à constante dielétrica K — como ela é triplicada C fica 3 vezes maior — U permanece constante — W=C.U2/2 — assim a nova energia armazenada ficará 3 vezes maior — R- C
23- C=Q/U — 8.10-11=Q/12 — Q=96.10-11C — regra de três — 1 e – 1,6.10-19C — n e – 96.10-11C — n=6,0.109 eletrons — R- C
24-

25- R- E — veja teoria
26- Veja sequência abaixo:
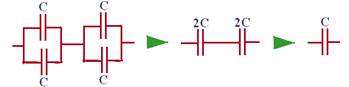
R- D
27- Os dois últimos capacitores estão em circuito aberto e não participam — observe a seqüência abaixo —

R- C
28- Observe a seqüência abaixo:

R- B
29–
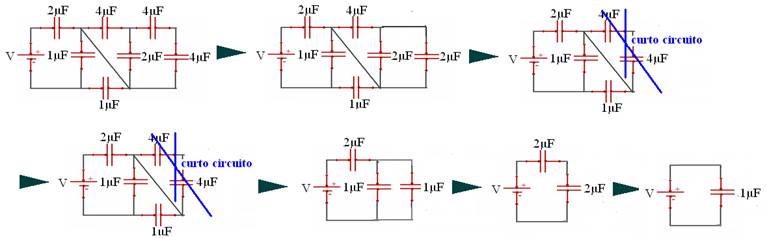
R- C
30- Os capacitores C2 e C3 estão ligados em paralelo e a capacitância equivalente dos dois é Ceq = 2C. Portanto a diferença de potencial no capacitor C1=C será o dobro. Ficamos então com 60 V no capacitor C1 — R- 60V
31- O capacitor equivalente de área A e distância entre as placas d’ que está em paralelo com os três capacitores C de área A e distância d vale Ceq=3C — εA/d’=3εA/d — d’=d/3 — R- A
32- a)Como estão em paralelo — Ceq=1.400.10-6 + 1.400.10-6 — Ceq=2,800.10-6F — Ceq=Q/U — 2.800.10-6=Q/170 — Q=0,476C
b) W=C.U2/2=2.800.10-6.(170)2/2 — W=40.460.000.10-6 — W=40,46J
33- C1 e C2 estão em paralelo — C’=2,0μF — C’ está em série com C3=3μF — veja figura abaixo —
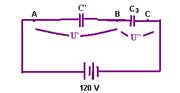
como C’ está em série com C3, eles possuem a mesma carga Q — C’=Q/U’ — U’=Q/2.10-6 — U’’=Q/3.10-6 — U’ + U’’=120 — Q/2.10-6 +
Q/3.10-6=120 (I) — C’=Q/U’ — Q=2.10-6U’ (II) — (II) em (I) — 2.10-6U’2.10-6 + 2.10-6U’=120 — U’ + 2/3U’=120 — 3U’+ 2U’=360 — U’=360/5 — U’=72V — U’’=120 – 72 — U’’=48V
34-  R- A
R- A
35- Observe na seqüência abaixo o cálculo da capacitância do capacitor equivalente —
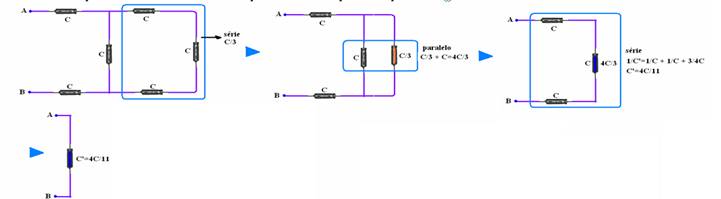
C’=Ceq=4C/11=4.11.10-6/11 — Ceq=4.10-6F — Ceq=Q/U — 4.10-6=Q/10 — Q=4.10-5C — R- B
36- Todas estão corretas — veja teoria
37- A capacitância de um capacitor é dada por C = q/U de onde vem => U = q/C
No circuito em série — ε = U1 + U2 — ε = (q/C1) + (q/C2) => ε/q = (1/C1) + (1/C2) — ε/q=(C1 + C2)/(C1 .C2)
No circuito em paralelo — ε = U1 — ε = q1/C1 => q1 = ε.C1 — ε = U2 — ε = q2/C2 => q2 = ε.C2 — q1 + q2 = ε.C1 + ε.C2 = ε.(C1 +C2) = 4q — (C1 +C2) = 4q/ε => C1 = 4q/ ε – C2 — então — ε/q = (C1 + C2)/(C1 .C2) — ε/q = (4q/ε)/(C1 .C2) => C1 .C2 = 4q2/ε
C1 .C2 = 4q2/ε — (4q/ε – C2) .C2 = 4q2/ε — C22 – (4q/ε).C2 + (4q2/ε2) = 0 — C2 = 2q/ε — e ainda — C1 = 4q/ε – C2 = 4q/ε – 2q/ε — C1 = 2q/ε
38- C1 e C2 estão em paralelo — C’=(2 + 3).10-6 — C’=5.10-6F — observe a figura abaixo e note que, como as capacitâncias de C3
e de C’ são iguais, eles estão sob mesma ddp U=5V — C’=Q/U — 5.10-6=Q/5 — Q=25.10-6C — C1=Q1/U — 2.10-6=Q1/5 — Q1=10.10-6C — Q2=C2.U=3.10-6.5 — Q2=15.10-6C — Q3=C3.U=5.10-6.5 — Q3=25.10-6C — 1/Ceq=C’ série com C3=5/2.10-6C — Ceq=2,5.10-6C — Ceq=Q/U — 2,5.10-6=Q/5 — Q=12,5.10-6C — R- C
39- Associados em série — Ceq=2.3/(2 + 3)μC — Ceq=1,2.10-6C — Ceq=Q/U — 1,2.10-6=Q/100 — Q=120.10-6C — Q= 120μC — como estão em série essa carga é a mesma para os dois capacitores — R- C
40- Depois que o capacitor está carregado, não passa mais corrente por ele e o circuito fica conforme esquema abaixo:
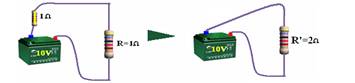
R’=U/i — 2=10/i — i=5 A — cálculo da ddp nos terminais do capacitor — R=U/i — 1-U/5 — U=5V — W=C.U2/2 —
W=4.10-6.(5)2/2 — W=50μJ
41- 01- Falsa — o capacitor fica com ddp de 6V
02- Falsa — a lâmpada ficará acesa até que o capacitor fique carregado
03- Falsa — não há curto circuito, existe a lâmpada
04- Falsa — C=Q/U — 2.10-6=Q/6 — Q=12.10-6C
05- Correta — W=C.U2/2=2.10-6.36/2 — W=3,6.10-5J
R- a correta é a 05
42- Refazendo o circuito:
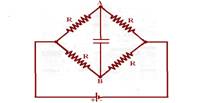
Observe que se trata de uma ponte de Wheatstone em equilíbrio, pois o produto das resistências opostas é nulo e, nessas condições o potencial em A é igual ao potencial em B — UAB=0 — R- A
43-

R- B
44- I. Correta — o capacitor carregado interrompe a corrente no ramo do circuito onde está inserido o capacitor e o amperímetro.
II. Correta — i=10/5 — i=2 A — R=U/i — 4=U/2 — U=8V — C=Q/U — 2.10-6=Q/8 — Q=16μC.
III. Falsa — é 8V — veja II.
VI. Falsa — é 2 A — veja II.
R- B
45- a) Chave aberta — observe na seqüência abaixo que a tensão nos terminais do capacitor com a chave aberta é U=30V —

C=Q/U — 3.10-6=Q/30 — Q=90μC
b) Chave fechada —
Req=U/i — 20=30/i — i=1,5 A — o capacitor está no ramo onde tem o resistor de 10Ω e a tensão em seus terminais vale —
R=U/i — 10=U/1,5 — U=15V — C=Q/U — 3.10-6=Q/15 — Q=45μC
46- A corrente de curto circuito num gerador é fornecida por icc=E/r — 6=E/2 — E=U=12V — C=Q/U=2,4.10-11/12 —
C=2.10-12C — C=2pF — R- E
47- Tirando o capacitor e aplicando a lei de Pouillet — 200i + 300i -20 +10=0 — i=1/50 A — cálculo da tensão U nos terminais do capacitor — U=E – r.i=20 – 300.1/50 — U=14V — Q=C.U=2.10-6.14=28.10-6C —– Q=28μC — P=R.i2=500.(1/50)2 — P=0,2W — R- B
48- a) Como o capacitor perde 87,5% da sua carga em 3 ms, significa 3ms correspondem a 3τ (τ = R.C), então τ = 1 ms:
τ = R . C — 1 x 10-3 = 50 . C >>> C = 2 x 10-5 F — Q = C . U >>> Q = 2 x 20-5 x 5 x 103 = 0,1 C — Im = ΔQ/Δt = (0,875 x 0,1) / (3 x 10-3) = 29,2 A
b) A energia armazenada no capacitor é dada por E = (C . U2) / 2
E = [2 x 10-5 x (5 x 103)2] / 2 — E = 250 J
49- a) Cálculo da capacitância C da membrana de área 5,0.10-5cm2, se cada cm2 de área tem capacitância de 0,8.10-6F — regra de três — 1 cm2– 0,8.10-6F — C=5.10-5.0,8.10-6 — C=4.10-11 F — seja (n) a quantidade de íons, cada um com carga e=1,6.10-19C, então a quantidade de carga total (Q) que atravessará a membrana vale — Q=n.e=n.1,6.10-19 — Q=1,6.10-19.n — definição de capacitância — C=Q/U — 4.10-11 = 1,6.10-19.n/80.10-3 — n=2,0.107 íons.
b) Potência elétrica entregue ao conjunto de íons para despolarizar a membrana — P=i.U=(Q/∆t).U=(n./∆t).e.U — P=5.108.1,6.10-19.20.10-3— P=1,6.10-12 W.
50- a) Cargas negativas (íons negativos – Cl–) deslocam-se para pontos de maior potencial, do interior para o exterior da célula — cargas positivas (íons positivos – Ca2+) deslocam-se para pontos de menor potencial, do exterior para o interior da célula.
b) No interior da membrana (interior do capacitor), pelo gráfico a ddp U=(64.10-3 – 0)=64.10-3m — U=E.d — 64.10-3=E.8.10-9 — E=8,0.106V/m ou N/C.
c) Força elétrica sobre os íons Cl– — FCl=|q|.E=1.1,6.10-19.8.106 — FCl=1,28.10-12N — força elétrica sobre os íons Ca2+ — FCa=|q|.E=2.1,6.10-19.8.106 — FCl=2,56.10-12N.
d) Pela definição de capacitância, sendo Q a carga elétrica na superfície externa da membrana — C=Q/U — 12.10-12=Q/64.10-3 — Q=7,68.10-13C.
51- Observe que, da maneira como eles estão ligados você pode considerá-los como associados em série — a expressão matemática da capacitância de um capacitor é C=ε.S/D — no caso,
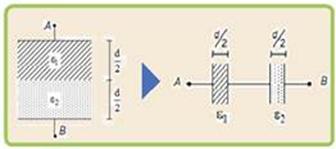
C1=ε1.S/(d/2) e C2=ε2.S/(d/2) — na associação série de capacitores a capacidade do capacitor equivalente é dada por — Ceq=produto/soma=C1.C2/(C1 + C2) — Ceq= [ε1.S/(d/2). ε2.S/(d/2)]/[ε1.S/(d/2) + ε2.S/(d/2)] —Ceq=2.ε1.ε2.S/d(ε1 + ε2) — Q=Ceq.U — Q=2.ε1.ε2.S/d(ε1 + ε2).U — R- C
