|
|
RESOLUÇÕES
01- A força resultante na direção do movimento é a força de atrito, constante, contrária ao mesmo que produz uma aceleração de retardamento também constante de intensidade FR=Fat=ma --- V=Vo - at --- função de primeiro grau (reta decrescente), velocidade diminuindo até parar, quando V=0.
R- B
02- Pelo enunciado as temperaturas final e inicial são iguais, portanto trata-se de uma transformação isotérmica (mesma temperatura T) onde P.V=constante. Observe nessa expressão que, depois de aberta a válvula o gás dobra seu volume e, para que o produto PxV seja constante a pressão anterior P1 deve cair pela metade.
R- A
03- Define-se momento (ou torque) de uma força de intensidade F aplicada num ponto P de uma barra, que pode girar livremente em torno de um ponto O (denominado polo) ao produto da intensidade dessa força F pela distância d do ponto de aplicação da força até o ponto O. Essa distância d é denominada de braço da força.
![]()
Equilíbrio de rotação --- A soma algébrica dos momentos das forças que agem sobre o sistema, em relação à qualquer ponto (polo O),deve ser nula.
Considere a seguinte situação esquematizada na figura abaixo:

Momento da força peso da pedra --- Mp= - F.d= - P.d1 --- momento da força F plicada pelo trabalhador --- MF= + F.d= + F.d2.
Equilíbrio de rotação --- A soma algébrica dos momentos das forças que agem sobre o sistema, em relação à qualquer ponto (polo O),deve ser nula --- - P.d1 + F.d2 = 0 --- F.d2 = P.d1 --- F = P.(d1/d2) ---
Observe nessa expressão que, como a força peso é a mesma (mesma pedra) a força F é diretamente proporcional a (d1/d2) --- assim, quanto menor d1 e maior d2 menor será a razão (d1/d2) e, consequentemente menor será a intensidade da força F aplicada pelo trabalhador.
R- A
04- Cálculo das resistências --- R1=V1/i1=8/2=2Ω --- R2=V2/i2=4/2=2Ω --- R3=V3/i3=4/2=2Ω --- R1=R2=R3.
Cálculo das potências --- P1=i1.V1=4.8=32W --- P2=i2.V2=2.4=8W --- P3=i3.V3=2.4=8W --- P1 > P23
R- D
05- Pelo teorema de Stevin a pressão no fundo de cada recipiente depende apenas de P=Patmosférica + dágua.g.hcoluna líquida --- como todos esses elementos são iguais em (I) e em (II), PI = PII.
R- C
06- a) Observe na figura abaixo onde foi considerada a onda representada pela linha cheia que o

comprimento de onda λ que corresponde à distância percorrida pela onda até começar a repetição vale λ=4m.
b) Período T é o tempo que a onda demora para percorrer 1λ (até começar a repetição) que,

observado na figura 2 acima nos fornece T=8s
c) Observe na figura 1 que a onda com curva tracejada está deslocada de um quarto de comprimento

de onda em relação à onda com curva cheia. Portanto a segunda foto (instante t1) foi tirada ( ao menos) um quarto de período depois, ou seja 8/4=2s. Os valores possíveis de t1 são (0 + 2=2s), (8 + 2=10s), (16 + 2=18s), etc. O valor mínimo é 2s
07- a) Pelo enunciado, um minuto (t=60s) após a ultrapassagem o veículo 1 tinha percorrido V1=S1/t --- (60/3,6)=S1/60 --- S1=3600/3,6 --- S1=1000m e, no mesmo instante (t=60s) o veículo 1 que estava a
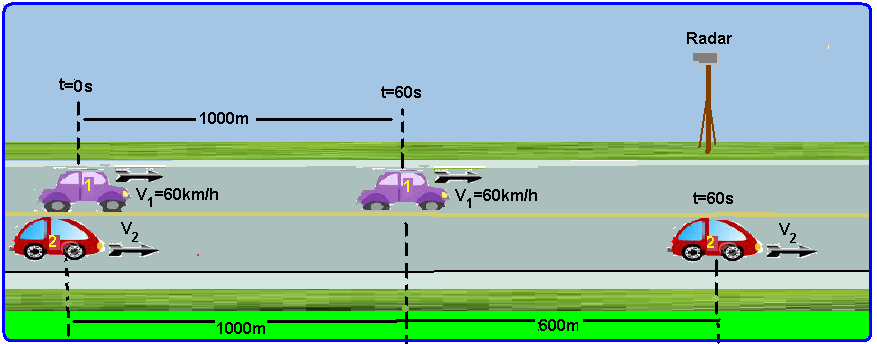
600m do radar e que já havia percorrido 1000m, viu o veiculo 2 passar pelo radar --- assim, após t=60s o carro 2 tinha percorrido a distância S2=1000 + 600=1600m com velocidade V2=S2/t=(1600/60)x
3,6=96km/h --- V2=96km/h.
Como eles se movem no mesmo sentido a velocidade relativa entre eles é a diferença entre as velocidades de cada um --- VR=96 – 60 --- VR=36km/h
b) O segundo veículo não ultrassou a velocidade de 100km/h, teve velocidade de 96km/h conforme ítem (a).
08- a) Energia mecânica no ponto I --- EmI=mgh + mV2/2= mgh + m02/2 --- EmI=mgh
Energia mecânica no ponto II --- EmII= mgh + mV2/2= mg0 + mV2/2 --- EmII=mV2/2
Pelo teorema da conservação da energia mecânica --- EmI=EmII --- mgh=mV2/2 --- V=√(2gh)
b) No ponto II as forças que agem sobre o corpo são seu peso (vertical e para baixo) e força de tração no fio (vertical e para cima) --- em todo corpo em movimento circular surge uma força
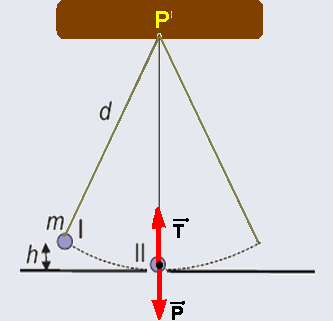
resultante centrípeta de direção radial, dirigida para o centro da circunferência (no caso, para cima) e de intensidade Fc=mV2/R=mV2/d --- mas, Fc=T – P --- mV2/d = T – mg --- m.(√(2gh)2 /d = T – mg ---
m.2gh/d = T – mg --- T=mg + 2mgh/d --- T=mg(1 + 2h/d)
