Assista a resolução em vídeo aula!

RESOLUÇÕES

 

01- a) Em todo lançamento oblíquo o movimento na direção horizontal é retilíneo e uniforme, com velocidade  horizontal , valendo  ---  V_x=V_ox=V_ocos45^o  ---  V_ox=V_o.√2/2  ---  V_ox=1,4V_o/2  ---  V_ox=(√2/2)V_o  ---  equação do movimento na horizontal  ---  x=x_o + V_oxt  ---  para percorrer os x=80m na horizontal ele demora certo tempo t  ---  80=0 + (√2/2)V_ot  ---  t= 80√2/V_o (I)  ---  na direção vertical quando a bola chega ao solo, no instante t, ela ocupa a

ordenada y=-0,5m sendo lançada com velocidade inicial vertical V_oy=V_osen45^o  ---  V_oy=(√2/2).V_o  ---  equação de um lançamento vertical  ---

y=y_o + V_oyt – gt²/2  ---  - 0,5 = 0 + (√2/2).V_o.80√2/V_o – 5.t²  ---  -0,5 = 80 - 5t²  ---  t²=80,5/5=16,1  ---  t≈4s (tempo que demora para percorrer 8om na horizontal, que é o mesmo tempo que demora para subir, descer e chegar ao solo)  ---  substituindo t=4s em (I)  ---   t= 80√2/V_o  ---  4= 80√2/V_o  ---  V_o = 80√2/4=28m/s  ---  V_o=28m/s ou V_o=20√2m/s.

b) Na altura máxima a componente vertical da velocidade é nula (V_y=0)  ---  equação de Torricelli  ---  V_y² = V_oy² – 2.g.h_max  ---  0² = [V_o. (√2/2)]² – 2.10.h_max  ---   0² = [20√2.(√2/2)]² – 2.10.h_max  ---  0²=400 – 20h_max  ---  h_max=20m (em relação ao ponto de lançamento)  ---  em relação ao solo a altura máxima atingida será  ---  H_max=20,0 + 0,5  ---  H_max=20,5m.

02- a) Área da base de cada cilindro A₁=A₂=A=π.R²=3.1²  ---  A=3cm²  ---  volume do cilindro 1  ---  V=A.h₁=3.5  ---  V₁=15cm³  ---  volume do cilindro 2  ---  V=A.h₂=3.0,5  ---  V₁=1,5cm³  ---  massa do cilindro 1  ---  d₁=m₁/V₁  ---

 

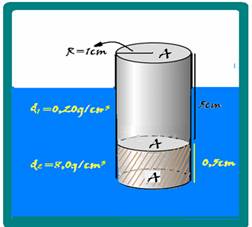
0,2=m₁/15  ---  m₁=3g  ---  massa do cilindro 2  ---  d₂=m₂/V₂  ---   8=m₂/1,5  ---  m₂=12g  ---   massa total  ---  m=3 + 12=15g  ---  m=15g ou m=15.10^-3kg.

b) Peso do cilindro  ---  P=m.g=15.10^-3.10  ---  P=15.10^-2N  ---  cálculo do empuxo sobre o cilindro com volume imerso V_i  ---  E=d_água.V_i.g=10³.V_i.10  ---  E=10⁴V_i   ---  como o está em equilíbrio o peso deve anular o empuxo  ---  P=E  ---

15.10^-2 = 10⁴V_i  ---  V_i=15.10^-6m³  ---  V_i=15cm³  ---  altura (h_i) da parte imersa  ---  V_i=S.h_i  ---  15=3.h_i    ---  h_i=5cm.

03- a) Observe pelo gráfico que no estado sólido, enquanto a temperatura do corpo sobe de O^oC até 4^oC o corpo absorve a quantidade de calor de Q₁=400cal  ---  calor específico no estado sólido (c_s)  ---  Q₁=m.c_s.(θ – θ_o)  ---  400 =

100.c_s.(40 – 0)  ---  c_s=400/4000  ---  c_s=0,1caç/g^oC  ---  na fase líquida enquanto a temperatura do corpo sobe de 40⁰C para 60^oC são absorvidas Q₂=(1200 – 800)=400cal  ---  Q₂=m.c_l. (θ – θ_o)  ---  400=100.c_l.(60 – 40)  ---  c_l=400/2000  ---  c_l=0,2cal/g^oC.

b) A fusão ocorre quando a substância passa de sólido a 40^oC para líquido a 40^oC , assim sua temperatura de fusão é

40^oC  ---  para se fundir ela recebe Q₃=800 – 400=400cal  ---  calor latente de fusão  ---  Q₃=mL_f  ---  400=100L_f  ---

L_f=4cal/g.   

04- a) Estando esses aparelhos funcionando normalmente, todos eles estão submetidos à mesma ddp (tensão) que é de U-110V e, para que isso ocorra, todos esses aparelhos devem estar associados em paralelo.

Como todos os aparelhos estão funcionando dentro das especificações comerciais, a potência total dissipada é a soma da potência de cada um desses aparelhos  ---  P_total=40 + 40 + 20 + 120=220W  ---  P_total=i_total..U  ---  220= i_total.110  ---

i_total=2 A.

b) Tempo de funcionamento  ---  ∆t=30diasx4h=120h  ---  P_total=W/∆t  ---  220W=W/120h  ---  W=26400W=26,4kWh  ---  custo  ---  C$=26,4x0,30=7,92  ---  C$=7,92 reais.

05- a) Pelo enunciado  ---  razão focal da objetiva=distância focal da objetiva (f_ob)/diâmetro da objetiva  ---  19=f_ob/102  ---  f_ob=19x102  ---  f_obj=1938cm=19,38m  ---  observe que a distância focal da objetiva (f_ob=19,38m) é maior que o

comprimento do telescópio (L=19,20m) o que inviabiliza o exercício  ---  ou, como  a soma das distâncias focais da objetiva e da ocular é igual ao comprimento L do telescópio, você tem  ---  f_ob + f_oc =L  ---  19,38 + f_oc=19,20  ---

f_oc= - 0,18cm (esse resultado é impossível, pois o enunciado afirma que a lente ocular é convergente e obrigatoriamente sua distância focal deveria ser positiva).

b)O aumento visual, ou ampliação angular (aumento angular) é fornecido por  ---  G=f_ob/f_oc, mas, como os dados estão incorretos, não continuaremos a resolução.

06- a) É dado C=35cm e que a razão C/L^2/3 é próxima (aproximadamente igual) a 7/1  ---  C/L^2/3 =7/1  ---  35/L^2/3 =7/1  ---  L^2/3=35/7  ---  L^2/3=5  ---  L=√(5³)  ---  L=√125  ---  L=5.√5=5x2,2  ---  L=11cm (se L>11cm, ele não poderá se manter em pé).

b) Pelo enunciado C/L^2/3 =5,8/1 e L=135cm  ---  C/(135)^2/3 = 5,8/1  ---  C=5,8x(135)^2/3  ---  C=5,8x(27.5)^2/3  ---  C =

5,8x27^2/3x3^2/3=5,8x3²x1,7²  ---  C=150,86cm.

 

 

 

Exercícios