RESOLUÇÕES

 

01- a) Entre 1 e 2 trata-se de uma transformação isotérmica cujas características são fornecidas a seguir: 

 Nela, durante todo o processo, a temperatura permanece constante (isso=igual; thermos=temperatura)  ---  o cientista Robert Boyle comprovou que, quando a temperatura é constante, a pressão (P) exercida por certa massa gasosa é inversamente proporcional ao volume (V) por ela ocupado  ---  ou  ---  P.V=constante  ---  ou ainda  ---  P_o.V­_o=P.V  ---  P e V_o representam a pressão e o volume num estado de equilíbrio inicial  ---  P e V representam a pressão e o volume num estado de equilíbrio final.

 Sendo P = k / V, se V tende a zero P cresce indefinidamente e se V cresce indefinidamente p tende a zero e, se você representar graficamente P x V você obterá uma curva de nome isoterma que é um ramo de uma hipérbole eqüilátera.

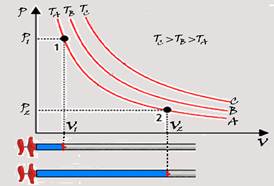
Cada ponto da curva (isoterma) A tem a mesma temperatura (T_A); Cada ponto da curva (isoterma) B tem a mesma temperatura (T_B) e cada ponto da curva (isoterma) C tem a mesma temperatura (T_C).

Pelo gráfico são fornecidos  ---  P₁=5.10⁵Pa, V₁=3.10^-5m³, P₂=3.10⁵Pa e V₂=?  ---  P₁.V₁=P₂.V₂  ---  5.10⁵.3.10^-5=3.10⁵.

V₂  ---  V₂=15.10^-5/3  ---  V₂=5.10^-5m³.

b) No trecho compreendido entre 2 e 3 ocorre uma transformação adiabática cuja expressão matemática é  P.V^γ=constante, ou seja, P₂.V₂^γ =P₃.V₃^γ  ---  P₃=P₂.V₂^γ /V₃^γ   ---  substituindo os respectivos valores  ---  P₃=3.10⁵.

(5.10^-5/6.10^-5) ^3/2 = 3.10⁵.√5³/6³)  ---  P₃=3.10⁵.√0,58=3.10⁵.0,77  ---  P₃≈2,3.10⁵Pa.

02- a) Observe na seqüência abaixo o cálculo da resistência do resistor equivalente (R_eq)  ---  R_eq=U/i  ---  4,5.10³=12/i   

---  i=12/4,5.10³  ---  i=2,7.10^-3A=2,7mA.

b) Observe na figura abaixo os valores das correntes devidamente distribuídas  ---  entre os pontos B e C, R=1kΩ e

i=1,35.10^{-3 A  ---  R=U/i  ---  1.103}=U/1,35.10^-3  ---  U=1,35.10^-3.10³  ---  U=1,35V.

03- a) As forças que agem sobre um corpo apoiado sobre um plano inclinado são seu peso, vertical e para baixo e a força normal , perpendicular à superfície de contato entre o bloco e o plano (figura abaixo).

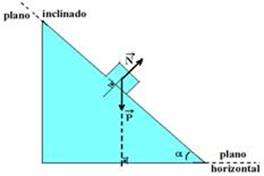
α é o ângulo de inclinação do plano. Como  e  não tem a mesma direção, vamos decompor o peso  em duas parcelas:

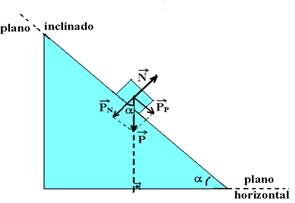
 parcela do peso paralela à superfície do plano inclinado (responsável pela tentativa de descida do bloco).

 parcela do peso perpendicular à superfície do plano inclinado (força que comprime o bloco contra o plano)

senα=cateto oposto/hipotenusa  ---  senα=P_p/P  ---  P_p=P.sena

cosα=cateto adjacente/hipotenusa  ---  cosα=P_N/P  ---  P_N=P.cosa

      

 

As duas forças acima substituem o peso e podemos tirá-lo:

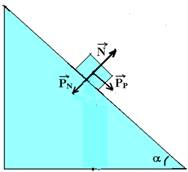
A componente normal do peso  anula a reação normal do apoio , assim temos:

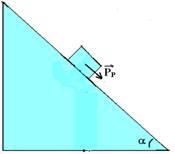
Como não existe atrito, o bloco desce com aceleração de intensidade a, tal que F_R=m.a  ---   P_p=m.a  ---  mgsenα=ma  ---  a=gsenα.

Como o bloco está em equilíbrio na direção perpendicular à superfície do plano inclinado  ---  N=P_N=Pcos30^o=10.√3/2  ---  N≈5.1,7≈8,5N.

b) Veja em (a) que ele desce com aceleração a=gsen30⁰=10.1/2  ---  a=5m/s²  ---  aplicando Torricelli  ---  V²=V_o² +

2.a.∆S  ---  10²=0² + 2.5.d  ---  d=100/10  ---  d=10m.

c) Como não existe atrito o bloco 1 atinge o bloco 2 com velocidade de V₁=10m/s  ---  antes do choque  ---  V₁=10m/s  ---  V₂=0  ---  quantidade de movimento do sistema antes do choque  ---  Q_sa=m₁V₁ + m₂V₂=1.10 + 3.0  ---  Q_sa=10kg.

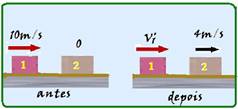
m/s  ---   depois do choque  ---  V’₁=?  ---  V₂=4m/s  ---  quantidade de movimento do sistema depois do choque  ---  Q_sd=m₁V’₁ + m₂V₂=1.V₁’ + 3.4  ---  Q_sd= V₁’ + 12  ---  pelo princípio da conservação da quantidade de movimento  --- 

Q_sa=Q_sd  ---  10 = V₁’ + 12  ---  V₁’= - 2m/s  (o sinal negativo significa que o bloco 1 retornou após o choque).

d) Cálculo da energia mecânica do bloco 2 no ponto A de altura zero e onde V=4m/s  ---  E_mA=mV²/2 + mgh=3.4²/2 +

0  ---  E_mA=24J  ---  E_mB=mV_B²2 + m.g.R=3.V_B²/2 + 3.10.0,6  ---  V_B=√4=2m/s  ---  no ponto mais alto B, a força resultante sobre o bloco é a centrípeta, vertical e dirigida para o centro da circunferência (baixo), de intensidade  ---

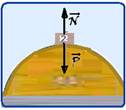
F_c=mV_B²/R  ---  P – N = 3.2²/0,6  ---  30 – N = 20  ---  N=10N.

04- O peso do corpo em Marte é o produto de sua massa que é a mesma em qualquer lugar ou planeta pela aceleração da gravidade na superfície do planeta Marte  ---  P=m.g=3,10x3,69=11,439N  ---  com três algarismos significativos  --- 

P=11,4N  ---  R- D.

05- I. Falsa  ---  O índice de refração de um meio representa a razão (comparação) entre a velocidade da luz no vácuo e  a velocidade da luz no meio, ou seja:

Veja nessa expressão que a velocidade da luz no meio V depende apenas da velocidade da luz no vácuo (c) e do índice de refração do meio(n).

II. Falsa  ---  quando um feixe de luz passa de um meio a outro sofrendo refração a única grandeza que não varia é a frequência que é a mesma da fonte emissora do feixe de luz.

III. Correta.

R- C.

06- Considerando os dois blocos como um único de massa M=(4 + 1)=5kg e sob ação da força de F=10N eles se movem com a mesma aceleração de F=Ma  ---  10=5.a  ---  a=2m/s² (aceleração de cada bloco)  ---  sobre o bloco 2 agem as forças de intensidades F=10N (horizontal e para a direita) e a força de atrito F_at (horizontal e para a esquerda)  

--- força resultante sobre o bloco 2  ---  F_R=F – F_at=10 - F_at  ---  F_R=m₂.a  ---  10 – F_at=1.2  ---  F_at=8N  ---  R- E.

07- Trata-se apenas de uma mudança de estado (fusão a 0^oC)  ---  Q=m.L_F=3.10.80=2400=2,4.10³cal  ---  R- E.

08- Dado  ---  q₂=2q₁ ---  d₂=(1 – q₁)  ---  E₁=kq₁/d₁²  ---  E₂=k2q₁/(1 – d₁)²  ---  campo elétrico resultante nulo  ---  E₁ =

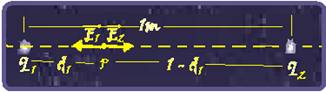
 E₂ ---  E₁=kq₁/d₁² = k2q₁/(1 – d₁)²  ---  1/d₁² = 2/(1 – d₁)²  ---  (1 – d₁)²/d₁²=2  ---  {(1 – d₁)/d₁}²=2  ---   {(1 – d₁)/d₁}=√2  ---  (1 – d₁)/d₁=1,4  ---  1,4d₁ = 1 – d₁  ---  d₁=1/2,4  ---  d₁=0,4m  ---  R- B.

09- Peso do chumbo quadrado  ---  P=m.g=0,030x10=0,3N  ---  peso dos triângulos de chumbo  ---  P=m.9=0,010x10=0,1N  ---  colocando as forças na haste maior e considerando o ponto O como pólo (figura)  ---  equilíbrio de rotação  ---  a soma dos momentos de cada força em relação ao pólo O deve ser nula  ---  M_0,3N= - F,d = -

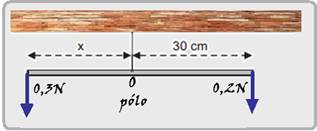
0,3.x  ---  M_0,2N = + F.d=+0,2.30 =6N.cm  ---  M_0,3N + M_0,2N=0  ---  - 0,3x + 6=0  ---  x=6/0,3  ---  x=20cm  ---    R- C.

10- V_m=∆S/∆t=(S – S_o)/(t – t_o)=(50 – 0)/(40 – 0)  ---  V_m=1,25m/s  ---  R- B.

11- Lei de Ohm  ---  resistor ôhmico, v é proporcional a i de modo que R seja constante  ---  R=V/i=6/3.10^-3=12/6.10^-3  ---  R=2.10³Ω=2kΩ  ---  R- D.

12- Os triângulos ABC e DEC são semelhante  ---  AB/DE = BC/EC  ---  4/1,6 = 6/S  ---  4S = 6x1,6  --- 

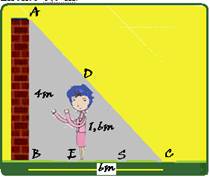
S=9,6/4=2,4m  ---  S=2,4m  ---  a distância pedida é do muro até a senhora  ---  d=6 – 2,4=3,6m  ---  R- D.

13- Ano luz  ---  d_a=v.t=3.10⁸.3,2.10⁷  ---   d_a=9,6.10¹⁵m  ---  nanômetro  ---  d_n=1.10⁹m  ---  ano luz em nanômetro=9,6.10¹⁵/1.10⁹=9,6.10²⁴nm  ---  R- A.

14- Dados  ---  R=380 000km  ---  T=28diasx24hx3600s=2 419 200s  ---  π=3  ---  V=2πR/T=2X3X380 000km/2 419 200s  ---  V=0,94km/s  ---  R- E.

15- Observe na sequência abaixo o cálculo da resistência do resistor equivalente  ---  R_eq=U/i  ---  1,5=3/i  ---  i=2A  ---

 

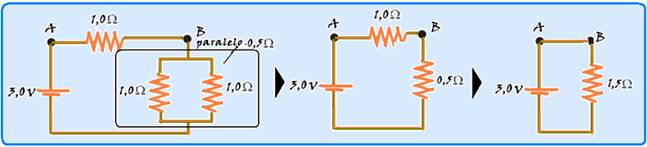
entre os pontos A e B flui uma corrente i=2A na resistência de R=1Ω  ---  R=U_AB/i  ---  U_AB=1.2=2V  ---  R- C.

16- Segundo a vertical, a componente da velocidade inicial vale V_oy=V_o.sen30^o=20.1/2  ---  V_oy=10m/s e a aceleração é a da gravidade g=10m/s²  ---  estudando o movimento na vertical você verifica que trata-se de um lançamento vertical para cima  ---  colocando a origem no ponto de lançamento, orientando a trajetória para cima e aplicando a equação de

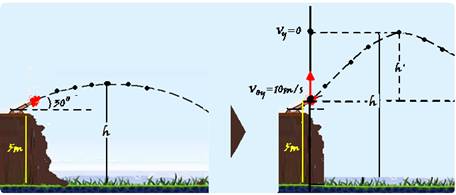
Torricelli lembrando que na altura máxima h’ a velocidade vertical é nula, V_y=0  ---  V_y² = V_oy² – 2.g.h’  ---  0² = 10² –

2.10.h’  ---  h’=100/20=5m  ---  como a altura pedida é em relação ao solo  ---  h=5 + 5=10m  ---  R- B.

17- O índice de refração de um meio representa a razão (comparação) entre a velocidade da luz no vácuo e  a velocidade da luz no meio, ou seja:

n=c/V  ---  1,5=3.10⁸/V  ---  V=3.10⁸/1,5  ---  V=2,0.10⁸m/s  ---  R- C.

18- Água  ---  V_a=0,01m³=0,01.10³dm³  ---  V_a=10L  ---  d_a=1g/cm³=10³kg/m³=10³kg/10³L  ---  d_a=1kg/L  ---  d_a=m_a/V_a  ---  1=m_a/10  ---  m_a=10L  ---  óleo  ---  V_o=2000cm³=2000.10^-3dm³  ---  V_o=2L  ---  d_o=0,9g/cm³=0,9.10³kg/m³=0,9.10³kg/10³L  ---  d_o=0,9kg/L  ---  d_o=m_o/V_o  ---  0,9=m_o/2  ---  m_o=1,8kg  ---  a massa da mistura vale  m=10 + 1,8=11,8kg  ---  R- A.

19- Intensidade da força magnética  sobre a carga  é proporcional a q, V, B e ao senθ, obedecendo à equação:

Pelo enunciado o ângulo entre o campo magnético e a trajetória da carga é 90^o (perpendiculares)  ---  F_m=q.V.B.sen90^o

---  F_m=q,V.B.1=1,6.10^-19.3.10⁸.8=38,4.10^-11N≈3,8.10^-10N  ---  R- A.

20- A distância entre dois nós consecutivos vale meio comprimento de onda (γ/2)  ---  γ/2=0,5  ---  γ=1,0m  --- 

R- C.

21- Utilizando o princípio da conservação da quantidade de movimento  ---  quantidade de movimento do sistema antes da colisão  ---  Q_sa=m_m.V_m + m_b.V_b=0,3.5 + 2,7.0  ---  Q_sa=1,5kgm/s  ---  quantidade de movimento do sistema depois

colisão, onde estão unidos, com velocidade V  ---  Q_sd=m_m.V_m + m_b.V_b=0,3.V + 2,7.V  ---  Q_sd=3V ---  Q_sa=Q_sd  --- 

da 1,5 = 3V  ---  V=0,5m/s  ---  R- D.

22- O torque, momento em relação ao pólo colocado em 0 (veja figura) é relativo à força P’=Psen30^o=mgsen30^o=4.10.1/2

  ---  P’=20N  ---  M=F,d=P’.d=20.0,2  ---  M=4N.m  ---  R- B.

 

 

Exercícios