|
|
RESOLUÇÕES
01- Movimento na vertical --- velocidade inicial vertical Voy=Vo.sen45o=30.√(2)/2=30.1,4/2=21m/s --- quando ele atinge a altura máxima h’ em relação ao ponto de lançamento --- Vy=0 --- trata-se de um lançamento vertical para cima com a=-g=-10m/s2 --- equação de Torricelli --- Vy2 = Voy2 + 2.(-g).h’ --- 02 = (21)2 – 2.10.h’ --- h’ = 441/20 --- h’=22,05m --- como ele foi lançado da altura de 12m, a altura máxima será --- hmax=12 + 22,05 --- hmax=34,05m
Ainda na vertical, quando ele atinge a base da coluna sua posição vertical vale y=-12m --- tempo que ele demora para
subir, atingir a altura máxima e chegar, na vertical, até a localização y=-12m --- Y = Yo + voyt – gt2/2 --- -12 = 0 +
21t – 10t2/2 --- 5t2 – 21t – 12 = 0 --- ∆=B2 – 4.A.C=(21)2 – 4.5.(-12) --- ∆=681 --- √∆=√681=26,1 --- t1=[-(-21) +
26,1]/10 --- t1=4,71s --- t2 fornece valor negativo e não é utilizável --- esse tempo t1=4,71s é o tempo que ele demora para percorrer o máximo alcance horizontal com velocidade constante Vox=Vo.cos450=30.1,4/2=21m/s --- Vox=Xmax/t1 --- 21=Xmax/4,71 --- Xmax=98,91m --- R- B.
02- As forças que agem sobre a caixa durante a descida com a=4m/s2 são --- parcela do peso responsável pela descida --- Pp=P.sen45o=m.g.√2/2=m.10.1,4/2 --- Pp=7m --- a força de atrito, contrária ao deslocamento é fornecida por ---
Fat= µ.N=µ.PN=µ.P.cos45o=µ.m.g.√2/2=µ.m.10.1,4/2 --- Fat=7µm --- a intensidade da força resultante sobre a caixa é
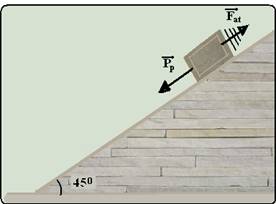
fornecida pela segunda lei de Newton --- FR=m.a --- FR=m.4 --- FR=Pp – Fat --- 4.m=7m – 7µm --- 4=7 – 7µ ---
µ=3/7=0,42 --- R- D.
03- Intensidade da quantidade de movimento (momento linear) da bola antes do choque com a parede --- Qa=m.V=0,3.6
Qa=1,8kg.m/s (N.s) --- Intensidade da
quantidade de movimento (momento linear) da bola depois do choque com a parede
--- Qd=m.V=0,3.6 --- Qd=1,8kg.m/s (N.s) --- teorema
do impulso ---
--- essa subtração é vetorial (veja
figura abaixo) --- observe nessa figura que o triângulo é eqüilátero e,
portanto o vetor
tem
também intensidade I=1,8N.s (kg.m/s) --- a intensidade do impulso também é fornecida por I=F.∆t --- 1,8=F.10-2 ---
F=1,8/10-2 --- F=180N --- R- B.
04- Observe a figura abaixo onde está representado o modo de vibração da frequência fundamental:
R- E.
05- O rendimento de uma máquina térmica é fornecido por uma das expressões abaixo:
Q1=4000J --- Q=5000J --- η=1 – 4000/5000=1 – 4/5=(5 – 4)/5=0,2 --- η=20% --- R- D.
06- Veja as informações abaixo:
Campo e potencial elétrico de um condutor esférico:
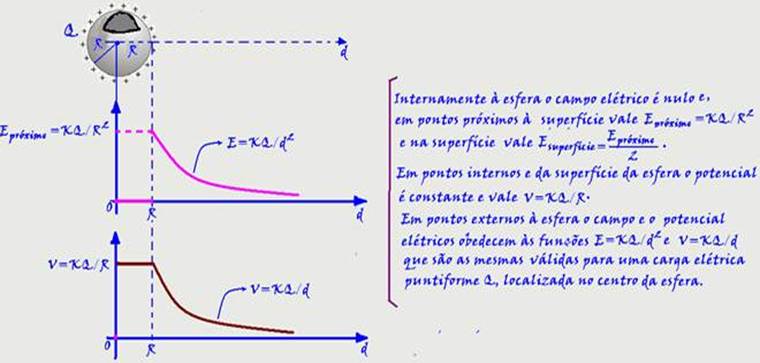
E=K.Q/d2=9.109.8.10-6/(3.10-1)2 --- E=72.103/9.10-2 --- E=8,0.105N/C --- R- C.
07- O fluxo magnético no interior de uma espira é fornecido por:
é o vetor normal ao plano que
contém a espira e α o ângulo que o vetor indução magnética
forma com.
Φ=B.S.cosα=2.10-5.(πR2).cos0o=2.10-5.3,14.(4.10-2)2.1 --- Φ=6,28.10-5.16.10-4 --- Φ=100,48.10-9Wb --- para 20 espiras --- Φ=20.100,48.10-9=2009,6.10-9=2,009.10-6Wb --- R- D.