Resoluções

01-Veja na figura abaixo a regra da mão esquerda colocada no ponto de entradadas carga e que é válida para carga

positiva,onde a força magnética está desviando a carga para a esquerda  ---  para a carga negativa a força tem mesma direção mas sentido contrário (para a direita) e a partícula neutra não sofre desvio.  R- E.

02- Carga elétrica q lançada com velocidade  lançada perpendicularmente às linhas de indução de um campo magnético uniforme   ---  observe que, neste caso o ângulo entre e é 90^o e que sen90^o=1.

Na figura abaixo uma carga positiva q penetra com velocidade   numa região em que existe um campo magnético uniforme  saindo da folha. Observe que e  são perpendiculares e, como a velocidade  é sempre tangente à trajetória em cada ponto, a força magnética , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma

circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é F_m=q.V.B.senθ=q.V.B.1  ---  F_m=q.V.B  ---  lembrando que a força magnética F_m é responsável pelo movimento circular é a força resultante centrípeta de intensidade F_c=m.V²/R  ---  F_m=F_c  ---  q.V.B=m.V²/R  --- observe na figura acima que R=x/2 --- q.B=m.V/x/2 ---  qBx/2=mV --- m=qBx/2V.

R- E

03- Você está no eixo Z observando o sistema de eixos cartesianos de cima para baixo e verá a situação conforme a figura 1 --- nela a corrente elétrica i no fio 1 está entrando na folha (plano XY) e a corrente no fio 2 saindo da mesma --- utilizando a regra da mão direita, onde você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida você fecha a mão

para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor (terceira figura). Observe na terceira figura que  é sempre tangente às linhas de indução em cada ponto --- observe no fio 1 que utilizando a regra da mão direita as circunferências terão o sentido horário e no ponto P o vetor B₁ originado pelo fio 1, que é tangente no ponto terá a direção e sentido indicados e no fio 2 que utilizando a regra da mão direita as circunferências terão o sentido anti horário e no ponto P o vetor B₂ originado pelo fio 2, que é tangente no ponto terá a direção e sentido indicados e --- a figura 2 mostra o vetor campo magnético

resultante em P e a o vetor velocidade da carga q aí lançada --- observe que B₁=B₂=B por simetria --- B_R=B₁cos a + B₂cosa ---

B_R=2Bcosa --- B=µi/2πd --- B_R=2.µi/2πd.cosa --- cosa=(L/2)/d --- cosa=L/2d --- B_R= B_R=2.µi/2πd.(L/2d) --- B_R= µiL/2πd² (I) --- força magnética que age sobre a carga q com velocidade V, perpendicular a B_R --- F_m=q.V.B_R.sen90^o=q.V.B_R.1 --- F_m=qVB_R (II) --- substituindo (I) em (II) --- F_m=q.V. (µiL/2πd²) --- F_m= µiLqV/2πd² --- R- C

04-Força elétrica --- quando uma carga elétrica q é colocada no interior de um campo elétrico uniforme surge sobre ela uma força elétrica com as seguintes características:

Sendo as cargas elétricas que penetram no campo elétrico uniforme positivas a força elétrica que

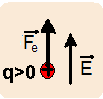
surgirásobre elas terá a mesma direção e sentido do campo, ou seja, vertical e para cima.

Força magnética --- quando uma carga elétrica positiva q é colocada no interior de um campo magnético uniforme surge sobre ela uma força magnética com as seguintes características:

 Direção e sentido de  - fornecidos pela regra da mão esquerda conforme mostrado na figura abaixo.

Observe na figura da direita que  é perpendicular a  e a , o que impõe a condição de que  e devem pertencer a um mesmo plano. Observe também que θ é o ângulo entre e 

 Intensidade de  - é proporcional a q, V, B e ao senθ, obedecendo à equação:

Pela regra da mão esquerda aplicada nas cargas ao penetrarem no campo magnético , a força magnética

que agirá sobre elas terá direção vertical e sentido para baixo (figura) e, sendo, pelo enunciado e

perpendiculares, o ângulo θ entre eles será de 90^o e a intensidade de será F_m=q.V.B.sen90^o --- F_m=q.V.B.

Análise de cada grupo, onde foram colocadas as forças elétrica e magnética :

Conclusão: V₁< V₃< V₂ e V₃=E/B --- R- E

05- Conforme o enunciado, existem dois dispositivos trabalhando no acionamento do atuador A, a lâmina bimetálica e o eletroímã:

Lâmina bimetálica – se surgir uma corrente elétrica de elevada intensidade percorrendo o disjuntor, a resistência R sofrerá um aquecimento, que será transmitido para o bimetal fazendo com que a temperatura do mesmo aumente e, pelo enunciado ele deverá tocar no atuador A, curvando-se para a direita --- para

que isso ocorra o metal x deverá se ditar mais que o metal y, ou seja, ΔL_x > ΔL_y e, nessas condições α_x > α_y

pois, a expressão ΔL=L_o.α.Δө mostra que o coeficiente de dilatação α é diretamente proporcional à dilatação ΔL).

Eletroimã E – observe na figura (1) fornecida pelo enunciado que a corrente elétrica está circulando no

eletroímã no sentido indicado na figura (2) --- quando o solenoide (eletroímã) é percorrido por corrente elétrica, a configuração de suas linhas de indução é obtida pela reunião das configurações de cada espira o que equivale à configuração das linhas de indução de um imã natural.

O sentido das linhas de indução, que indicam o sentido do campo magnético no interior do solenoide (eletroímã) é fornecido pela regra da mão direita (polegar no sentido da corrente e o sentido do campo magnético ou das linhas de indução magnética é no sentido da “fechada” da mão) aplicada em uma de suas

espiras (veja figuras acima) e em seu interior o campo magnético é praticamente uniforme e fora são linhas que saem do polo norte e chegam ao polo sul. Veja que o sentido do campo magnético criado ao longo do eixo do eletroímã apontará para a direta --- R- C

06-Carga elétrica q lançada com velocidade _o  perpendicularmente às linhas de indução de um campo magnético uniforme   ---  observe que, neste caso o ângulo entre e  é 90^o e que sen90^o=1.

Na figura abaixo uma carga positiva q penetra com velocidade  no ponto A numa região em que existe um campo magnético uniforme  penetrando na folha. Observe que e  são perpendiculares e, como a velocidade  é sempre tangente à trajetória em cada ponto, a força magnética , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de uma circunferência de raio R.

Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é F_m=q.V.B.senθ=q.V.B.(1)  ---  F_m=q.V.B  ---  lembrando que a força magnética F_m é responsável pelo movimento circular é a força resultante centrípeta de intensidade F_c=m.V²/R  ---  F_m=F_c  ---  q.V.B=m.V²/R  ---

   

 

R=m.V/q.B (I)  ---  o período T (tempo que a carga q demora para efetuar uma volta completa) é fornecido por  ---  V=ΔS/Δt  ---  numa volta completa  ---  ΔS=2πR e Δt=T  ---  V=2πR/T (II)  ---  substituindo II em I  ---R=m. (2πR/T)/q.B  ---  T=2πm/q.B (III) (tempo que o próton demora a efetuar uma volta completa)  

Utilizando os dados fornecidos na equação (I):

R- B

07- Carga elétrica q lançada com velocidade  lançada perpendicularmente às linhas de indução de um campo magnético uniforme   ---  observe que, neste caso o ângulo entre e é 90^o e que sen90^o=1.Na figura abaixo uma carga positiva q penetra com velocidade no ponto A numa região em que existe um campo magnético uniforme  penetrando na folha. Observe que e são perpendiculares e, como a velocidade  é sempre tangente à trajetória em cada ponto, a força magnética , obtida pela regra da mão esquerda e indicada na figura é sempre dirigida para o centro de

 uma circunferência de raio R. Assim, a carga q realizará um movimento circular uniforme com velocidade de intensidade constante .

A expressão matemática dessa força magnética é F_m=q.V.B.senθ=q.V.B.1  ---  F_m=q.V.B  ---  lembrando que a força magnética F_m é responsável pelo movimento circular é a força resultante centrípeta de

 intensidade F_c=m.V²/R  ---  F_m=F_c  ---  q.V.B=m.V²/R  --- B=mV/qR --- são dados --- m=5.10^-18 kg, q=8.10^-6C, V=4.10⁶m/s e R=5.10³cm=50m --- B=5.10^-18x4.10⁶/8.10^-6.50=(20/400).10^-6=0,05.10^-6 ---

B=5,0.10^-8 T --- R- D

08- Cargas elétricas em repouso não produzem campo magnético --- R- E

09- Utilizando a regra da mão esquerda, indicador (campo magnético) penetrando na folha, médio (velocidade) vertical e para cima, o polegar indicará a força sobre o próton (carga positiva) para a esquerda (1 ou 2).

Sendo o elétron carga negativa a força sobre ele estará em sentido contrário ao do próton e será para a direita (4 ou 5).

Quando a radiação gama passa por um campo magnético ela não sofre desvio, pois não são partículas eletrizadas, mas sim radiações eletromagnéticas --- assim essa radiação colide na posição 3.

Como o próton e o elétron penetram com a mesma velocidade e a massa do próton é muito maior que a massa do elétron, o próton sofre menor desvio atingindo a posição 1 e o elétron de menor massa, é mais desviado e atingre a posição 5.

R- E.

10- (V) Observe na figura abaixo a regra da mão esquerda com a força desviando a carga positiva

para a direita e a carga negativa para a esquerda.

(V) As partículas possuem cargas de sinais contrários já que a força magnética as desvia em sentidos opostos  ---  Partículas com a mesma velocidade e a mesma carga elétrica ao penetrarem num campo magnético uniforme com  perpendicular adescrevem trajetórias circulares de raios diferentes, pois na expressão R=m.V/q.B apenas R e m são variáveis, sendo os outros parâmetros constantes. Observe na expressão que R e m são diretamente proporcionais. Maior massa, maior o raio da curva.  ---  maior massa, menor valor q/m, pois q é a mesma para as duas cargas.

(F) na expressão R=m.V/q.B apenas R e q são variáveis, sendo os outros parâmetros constantes. Observe na expressão que R e q são inversamente proporcionais. Maior carga, menor o raio da curva e vice versa.. 

(F) Isolando o campo magnético B na expressão R=m.V/q.B, você obtém B=mV/qR onde B é inversamente proporcional a R, ou seja, quando um aumenta o outro diminui.

R- D

Exercícios