MOVIMENTO CIRCULAR UNIFORME (MCU)
MOVIMENTO CIRCULAR UNIFORME (MCU)
FORMULÁRIO
![]() Período e frequência
Período e frequência
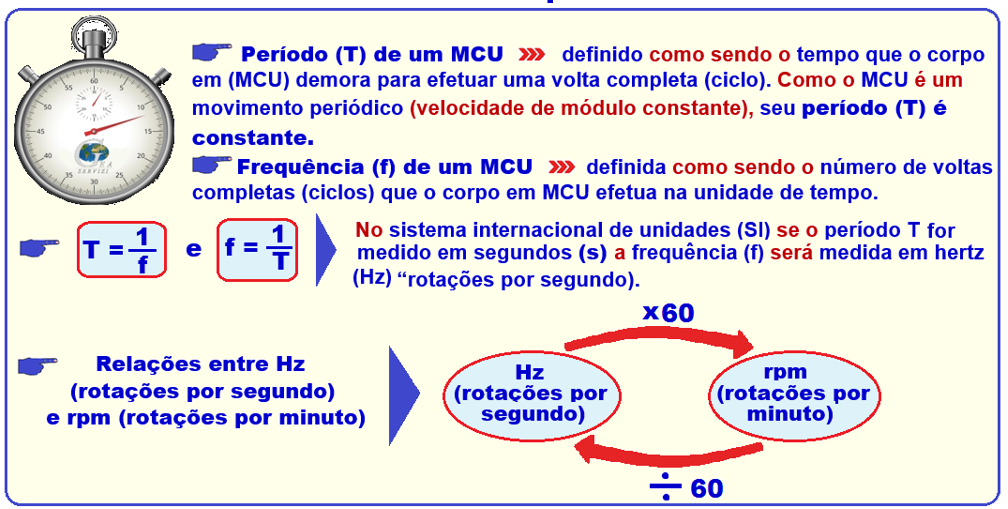
![]() Velocidade escalar (linear) V de um MCU
Velocidade escalar (linear) V de um MCU
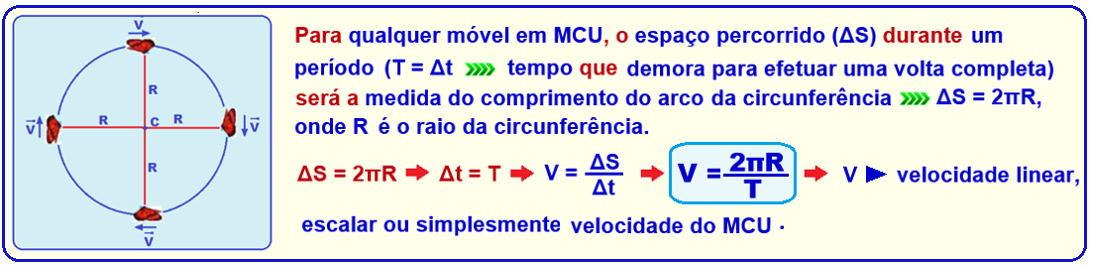
![]() Velocidade angular (W) de um MCU
Velocidade angular (W) de um MCU
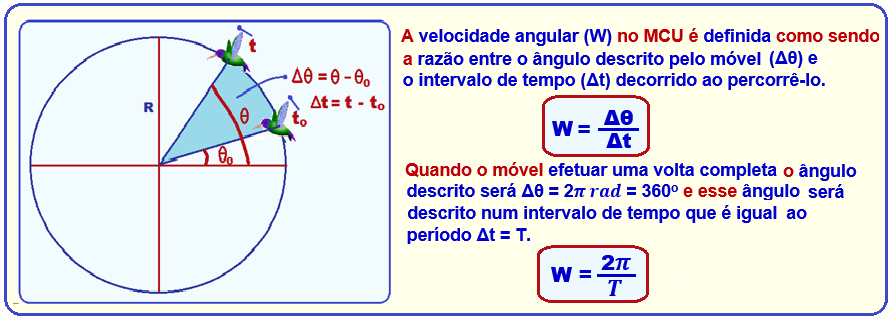
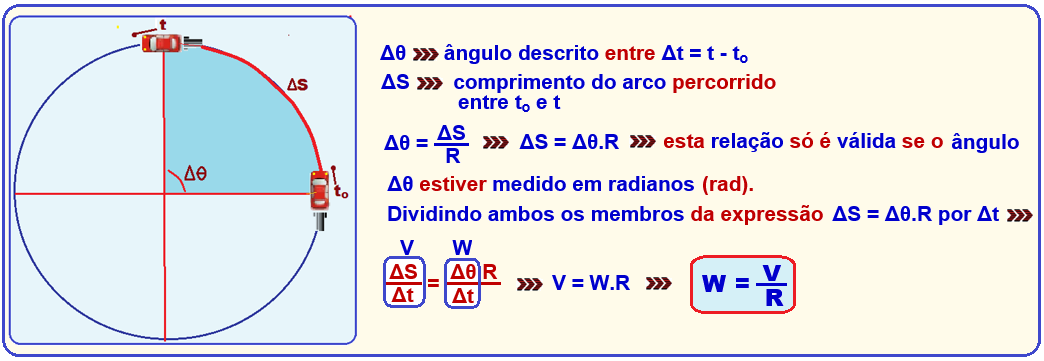
![]() Relação entre velocidade escalar (V) e velocidade angular (W)
Relação entre velocidade escalar (V) e velocidade angular (W)
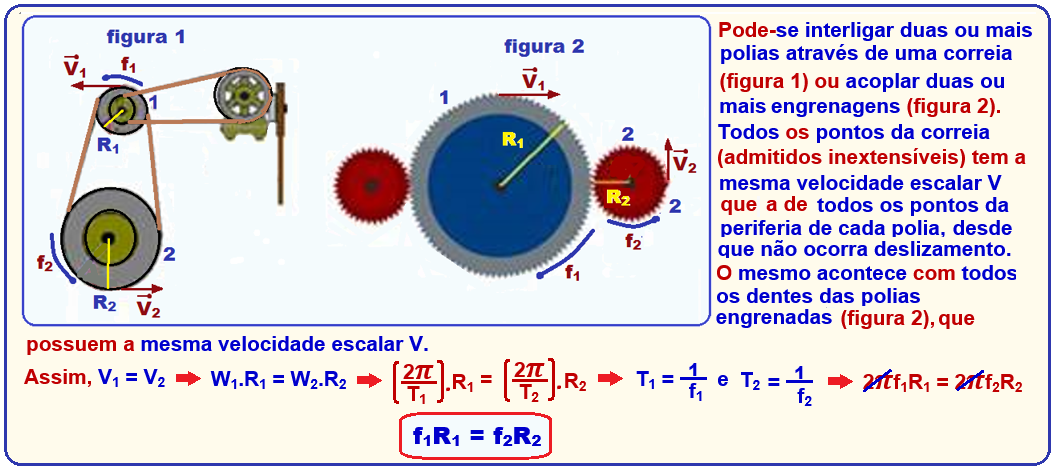
![]() Acoplamento de polias e engrenagens
Acoplamento de polias e engrenagens
Exercícios de vestibulares com resoluções comentadas sobre
Movimento Circular Uniforme
01-(UNESP-SP)

Quem está na Terra vê sempre a mesma face da lua. Isto ocorre porque:

a) a Lua não efetua rotação e nem translação.
b) a Lua não efetua rotação, apenas translação.
c) os períodos de rotação e translação da Lua são iguais.
d) as oportunidades para se observar a face oculta coincidem com o período diurno da Terra.
e) enquanto a Lua dá uma volta em torno da Terra, esta dá uma volta em torno do seu eixo.
02-(UFSM-RS)

Um trator tem as rodas traseiras maiores do que as dianteiras e desloca-se com velocidade constante.
Pode-se afirmar que, do ponto de vista do tratorista, os módulos das velocidades lineares de qualquer ponto das bandas de rodagem das rodas da frente (vf) e de trás (vt) e os módulos das velocidades angulares das rodas da frente (Wf) e de trás (Wt) são
a) vf > vt e Wf > Wt
b) vf > vt e Wf < Wt
c) vf < vt e Wf = Wt
d) vf = vt e Wf > Wt
e) vf = vt e Wf = Wt
03-(UNIFESP-SP)

Mãe e filho passeiam de bicicleta e andam lado a lado com a mesma velocidade.

Sabe-se que o diâmetro das rodas da bicicleta da mãe é o dobro do diâmetro das rodas da bicicleta do filho. Pode-se afirmar que as rodas da bicicleta da mãe giram com
a) a metade da freqüência e da velocidade angular com que giram as rodas da bicicleta do filho.
b) a mesma freqüência e velocidade angular com que giram as rodas da bicicleta do filho.
c) o dobro da freqüência e da velocidade angular com que giram as rodas da bicicleta do filho.
d) a mesma freqüência das rodas da bicicleta do filho, mas com metade da velocidade angular.
e) a mesma freqüência das rodas da bicicleta do filho, mas com o dobro da velocidade angular.
04-(UNICAMP-SP)

O quadro (a), abaixo, refere-se à imagem de televisão de um carro parado, em que podemos distinguir claramente a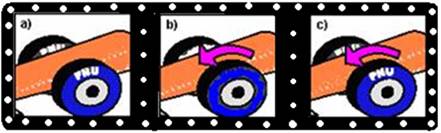
marca do pneu (“PNU”).
Quando o carro está em movimento, a imagem da marca aparece como um borrão em volta de toda a roda, como ilustrado em (b).
A marca do pneu volta a ser nítida, mesmo com o carro em movimento, quando este atinge uma determinada velocidade.
Essa ilusão de movimento na imagem gravada é devido à freqüência de gravação de 30 quadros por segundo (30 Hz).
Considerando que o diâmetro do pneu é igual a 0,6 m e π = 3,0, responda:
a) Quantas voltas o pneu completa em um segundo, quando a marca filmada pela câmara aparece parada na imagem, mesmo estando o carro em movimento?
b) Qual a menor freqüência angular W do pneu em movimento, quando a marca aparece parada?
c) Qual a menor velocidade linear (em m/s) que o carro pode ter na figura (c)?
05-(UFJF-MG)

Um velocímetro comum de carro mede, na realidade, a velocidade angular do eixo da roda, e indica

um valor que corresponde à velocidade do carro.
O velocímetro para um determinado carro sai da fábrica calibrado para uma roda de 20 polegadas de diâmetro (isso inclui o pneu).
Um motorista resolve trocar as rodas do carro para 22 polegadas de diâmetro. Assim, quando o velocímetro indica 100km/h, a velocidade real do carro é:
![]()
06-(FUVEST-SP)


A figura ilustra uma roda d’agua constituída de 16 cubas.
Cada cuba recebe 5L de água de uma bica cuja vazão é 160L/min. A roda gira em movimento uniforme.
a) Qual é o período de rotação da roda?
b) Qual é a quantidade de água utilizada em 1 hora de funcionamento do sistema?
07-(FUVEST-SP)

A Estação Espacial Internacional mantém atualmente uma órbita circular em torno da Terra, de tal forma que permanece sempre em um plano, normal a uma direção fixa no espaço.
Esse plano contém o centro da Terra e faz um ângulo de 40° com o eixo de rotação da Terra.
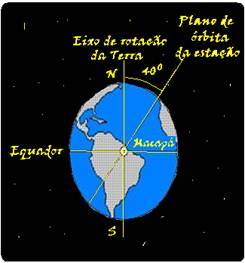
Em um certo momento, a Estação passa sobre Macapá, que se encontra na linha do Equador.
Depois de uma volta completa em sua órbita, a Estação passará novamente sobre o Equador em um ponto que está a uma distância de Macapá de, aproximadamente,

![]()
08-(UFU-MG)


Um relógio com mecanismo defeituoso atrasa 10 minutos a cada hora. A velocidade angular média do ponteiro maior desse relógio, quando calculada com o uso de um relógio sem defeitos, vale, em rad/s,
a) π/2160
b) π /2100
c) π /3600
d) π /1500
09-(UNESP-SP)

Satélites de órbita polar giram numa órbita que passa sobre os pólos terrestres e que permanece sempre em um plano fixo em relação às estrelas.
Pesquisadores de estações oceanográficas, preocupados com os efeitos do aquecimento global, utilizam satélites desse tipo para detectar regularmente pequenas variações de temperatura e medir o espectro da radiação térmica de diferentes regiões do planeta.
Considere o satélite a 5298 km acima da superfície da Terra, deslocando-se com velocidade de 5849 m/s em uma órbita circular.
Estime quantas passagens o satélite fará pela linha do equador em cada período de 24 horas.
Utilize a aproximação π = 3,0 e suponha a Terra esférica, com raio de 6400 km.
10-(UNESP-SP)

Um cilindro oco de 3,0 m de comprimento, cujas bases são tampadas com papel fino, gira rapidamente em torno de seu eixo com velocidade angular constante. 
Uma bala disparada com velocidade de 600 m/s, paralelamente ao eixo do cilindro, perfura suas bases em dois pontos, P na primeira base e Q na segunda.
Os efeitos da gravidade e da resistência do ar podem ser desprezados.
a) Quanto tempo a bala levou para atravessar o cilindro?
b) Examinando as duas bases de papel, verifica-se que entre P e Q há um deslocamento angular de 9°.
Qual é a freqüência de rotação do cilindro, em hertz, sabendo que não houve mais do que uma rotação do cilindro durante o tempo que a bala levou para atravessá-lo?
11-(UNESP-SP)

Um disco horizontal, de raio R = 0,50m, gira em torno de seu eixo com velocidade angular W = 2π
rad/s.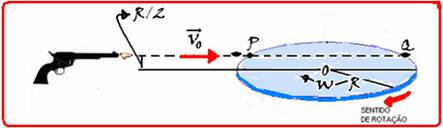
Um projétil é lançado de fora no mesmo plano do disco e rasante a ele, sem tocá-lo, com velocidade Vo (figura), passando sobre o ponto P.
O projétil sai do disco pelo ponto Q, no instante em que o ponto P está passando por aí pela primeira vez. Qual é a velocidade Vo?
12-(UNIFESP-SP)

Três corpos estão em repouso em relação ao solo, situados em três cidades: Macapá, localizada na linha do Equador, São Paulo, no trópico de Capricórnio, e Salekhard, na Rússia, localizada no círculo Polar Ártico.
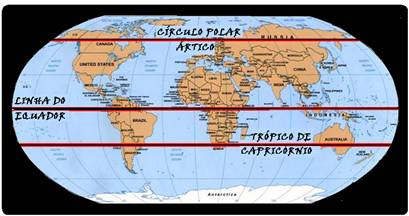
Pode-se afirmar que esses três corpos giram em torno do eixo da Terra descrevendo movimentos circulares uniformes, com
A) as mesmas freqüência e velocidade angular, mas o corpo localizado em Macapá tem a maior velocidade tangencial.
B) as mesmas freqüência e velocidade angular, mas o corpo localizado em São Paulo tem a maior velocidade tangencial.
C) as mesmas freqüência e velocidade angular, mas o corpo localizado em Selekhard tem a maior velocidade tangencial.
D) as mesmas freqüência, velocidade angular e velocidade tangencial, em qualquer cidade.
E) freqüência, velocidade angular e velocidade tangencial diferentes entre si, em cada cidade.
13-(FATEC-SP)

As rodas dentadas A, B e C têm, respectivamente, 32, 64 e 96 dentes, como mostra a figura.
Sabendo que C, de raio 12cm, tem velocidade angular de 6 rad/s, a velocidade linear de um ponto da periferia da roda B e a velocidade angular da roda A são, respectivamente:
a) 72 cm/s e 9,0 rad/s
b) 36 cm/s e 9,0 rad/s
c) 72 cm/s e 18 rad/s
d) 36 cm/s e 18 rad/s
e) 18 cm/s e 36 rad/s
14-(UFJF-MG)

No ato de manobrar seu carro para estacionar, uma motorista deixa um dos pneus raspar no meio fio. Com isso, uma

pequena mancha branca fica no pneu.
À noite, o carro está passando em frente a uma casa noturna iluminada por uma lâmpada estroboscópica com freqüência de 5Hz.
Nessa situação, uma pessoa olha e tem a impressão de que o pneu com a mancha branca está girando como se o carro estivesse se movendo para trás, embora ele esteja deslocando-se para frente.
Uma possível razão para isto é que a freqüência de rotação do pneu é
a) maior que 5 Hz e menor que 6 Hz.
b) maior que 4 Hz e menor que 5 Hz.
c) exatamente igual a 5 Hz.
d) maior que 10 Hz e menor que 11 Hz.
e) certamente maior que 5 Hz.
15-(UFRJ-RJ)

O olho humano retém durante 1/24 de segundo as imagens que se formam na retina.
Essa memória visual permitiu a invenção do cinema. A filmadora bate 24 fotografias (fotogramas) por segundo.
Uma vez revelado, o filme é projetado à razão de 24 fotogramas por segundo. Assim, o fotograma seguinte é projetado no exato instante em que o fotograma anterior está desaparecendo de nossa memória visual, o que nos dá a sensação de continuidade.
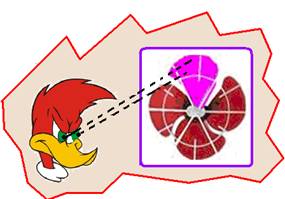
Filma-se um ventilador cujas pás estão girando no sentido horário. Este ventilador possui quatro pás simetricamente dispostas, uma das quais pintadas de cor diferente.
Ao projetarmos o filme, os fotogramas aparecem na tela numa sequência que nos dá a sensação de que as pás estão girando em sentido anti- horário.

Desta forma, o número mínimo de rotações por segundo que as pás devem estar efetuando, para que isto ocorra, é de:
![]()
16-(FATEC-SP)

Em um estádio esportivo, uma pista circular tem raio igual a 12,0 m.
Dois atletas A e B percorrem a pista no mesmo sentido com velocidades constantes VA = 8 m/s e VB = 6m/s. Ambos passam por um mesmo ponto na data zero.
O corredor mais veloz estará com uma volta de vantagem sobre o outro na data: (considere π = 3)
a) 35 s
b) 15 s
c) 20 s
d) 60 s
e) 36 s
17-(CEFET-CE)

Duas partículas percorrem uma mesma trajetória em movimentos circulares uniformes, uma no sentido horário e a outra no sentido anti-horário.
A primeira efetua 1/3 rpm e a segunda 1/4 rpm. Sabendo que partiram do mesmo ponto, em uma hora, quantas vezes se encontrarão?
18-(FGV-SP)

Uma grande manivela, quatro engrenagens pequenas de 10 dentes e outra de 24 dentes, tudo associado a três cilindros de 8 cm de diâmetro, constituem este pequeno moedor manual de cana.
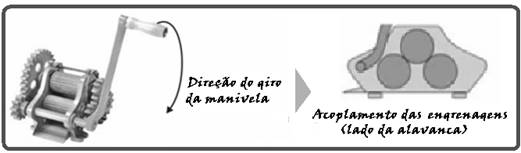
Ao produzir caldo de cana, uma pessoa gira a manivela fazendo-a completar uma volta a cada meio minuto.
Supondo que a vara de cana colocada entre os cilindros seja esmagada sem escorregamento, a velocidade escalar com que a máquina puxa a cana para seu interior, em cm/s, é, aproximadamente,
Dado: Se necessário use π = 3.
![]()
19-(UEL-PR) O cavalo anda nas pontas dos cascos.
Nenhum animal se parece tanto com uma estrela do corpo de balé quanto um puro sangue em perfeito equilíbrio, que a mão de quem o monta parece manter suspenso.
Degas pintou-o e procurou concentrar todos os aspectos e funções do cavalo de corrida: treinamento, velocidade, apostas e fraudes, beleza, elegância suprema.

Ele foi um dos primeiros a estudar as verdadeiras figuras do nobre animal em movimento, por meio dos instantâneos do grande Muybridge. De resto, amava e apreciava a fotografia, em uma época em que os artistas a desdenhavam ou não ousavam confessar que a utilizavam.
Suponha que a sequência de imagens apresentada na figura da esquerda foi obtida com o auxílio de câmeras fotográficas dispostas a cada 1,5 m ao longo da trajetória do cavalo.
Sabendo que a frequência do movimento foi de 0,5 Hz, a velocidade média do cavalo é:
![]()
20-(UERJ-RJ)

Um ciclista pedala uma bicicleta em trajetória circular de modo que as direções dos deslocamentos das rodas mantêm sempre um ângulo de 60o.
O diâmetro da roda traseira dessa bicicleta é igual à metade do diâmetro de sua roda dianteira.
O esquema mostra a bicicleta vista de cima em um dado instante do percurso.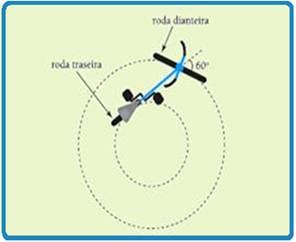
Admita que, para uma volta completa da bicicleta, N1 é o número de voltas dadas pela roda traseira e N2 o número de voltas dadas pela roda dianteira em torno de seus respectivos eixos de rotação.
A razão N1/N2 é igual a:
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
21-(PASUSP)

Uma bicicleta tem a roda dianteira com raio 27 cm e a roda traseira com raio 33 cm.
Estando a bicicleta parada, dois pontos A e B são marcados, nas rodas dianteira e traseira, nos respectivos pontos de contato com o solo, conforme a figura.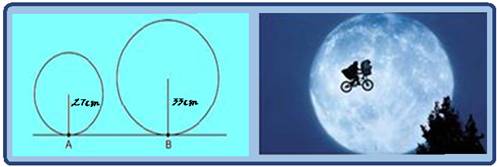
Depois de a bicicleta percorrer uma distância d, os pontos A e B voltam a ficar, simultaneamente, em contato com o solo.
Assumindo que não há escorregamento das rodas da bicicleta, o menor valor de d, em metros, para o qual essa situação acontece, é
![]()
22-(MACKENZIE-SP)

Num relógio convencional, às 3h pontualmente, vemos que o ângulo formado entre o ponteiro dos minutos e o das horas mede 90°. 
A partir desse instante, o menor intervalo de tempo, necessário para que esses ponteiros fiquem exatamente um sobre o outro, é
(A) 15 minutos.
(B) 16 minutos
(C) 180/11 minutos.
(D) 360/21 minutos.
(E) 17,5 minutos.
23-(ITA-SP)

Entre duas superposições consecutivas dos ponteiros das horas e dos minutos de um relógio, o ponteiro dos minutos varre um ângulo cuja medida, em radianos, é igual a
![]()
24- (UFJF-MG)

Na figura abaixo, quando o ponteiro dos segundos do relógio está apontando para B, uma formiga parte do ponto A e se desloca com velocidade angular constante W = 2π rad/min, no sentido anti-horário.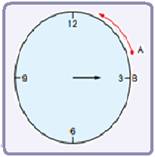
Ao completar uma volta, quantas vezes a formiga terá cruzado com o ponteiro dos segundos?
a) zero
b) uma
c) duas
d) três
e) π
25-(FUVEST-SP)

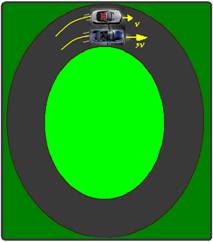
Dois carros percorrem uma pista circular, de raio R, no mesmo sentido, com velocidades de módulos constantes e iguais a v e 3v. O tempo decorrido entre dois encontros sucessivos vale:
a) π R/3v.
b) 2π R/3v.
c) π R/v.
d) 2π R/v.
e) 3π R/v.
26-(OBF)


Beto e Pedro são dois malabaristas em monociclos onde os pedais acionam diretamente os eixos das rodas.
Para que se mantenham lado a lado, em movimento uniforme, Beto dá 3 pedaladas completas por segundo enquanto Pedro dá apenas 2.
O monociclo de Beto tem raio de 30 cm.
a) qual o raio do monociclo de Pedro?
b) num determinado instante, qual a velocidade do ponto de contato da roda com a pista, admitindo que não ocorra deslizamento? E de um ponto diametralmente oposto ao ponto de contato?
27-(UFC-CE)

Um automóvel se desloca em uma estrada horizontal com velocidade constante de modo tal que os 
seus pneus rolam sem qualquer deslizamento na pista.
Cada pneu tem diâmetro D = 0,50 m e um medidor colocado em um deles registra uma freqüência de 840 rpm.
A velocidade do automóvel é, aproximadamente, de: (considere π = 3).
a) 32,4km/h
b) 43,2km/h
c) 54,0km/h
d) 64,8km/h
e) 75,6km/h
28-(UEM-PR)

Um modelo padrão para dar movimento a uma bicicleta consiste em duas polias conectadas por uma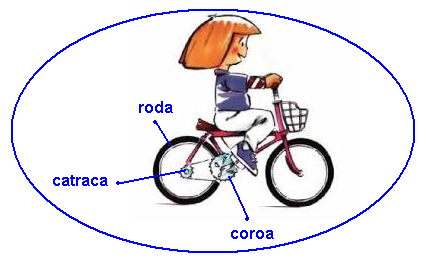
corrente.
Uma das polias, chamada de coroa, fica conectada aos pedais, enquanto a outra polia, chamada de catraca, fica acoplada à roda traseira da bicicleta.
Cada pedalada, isto é, cada giro completo dos pedais, corresponde a um giro completo da coroa, enquanto cada volta completa da catraca corresponde a uma volta completa da roda à qual está acoplada.
Sabe-se, ainda, que o número de voltas da catraca é proporcional ao número de voltas da coroa, com razão de proporção igual à razão entre os raios da coroa (R) e da catraca (r).
Considerando que a bicicleta, a partir do modelo apresentado, desloca-se em linha reta em uma superfície plana e que não haja deslizamento entre as rodas da bicicleta e a superfície, assinale o que for correto.
01) Se os raios da coroa e da catraca são, respectivamente, R e r, então cada volta completa da
coroa corresponde a R/r voltas da catraca.
02) Para um dado R fixo, quanto menor for o raio da catraca, maior será o deslocamento da bicicleta por pedalada realizada.
04) As velocidades angulares da coroa e da catraca são sempre iguais, independentemente do valor de seus raios.
08) Se a coroa de uma bicicleta tem raio igual a 15 cm, e a catraca tem raio igual a 1/5 do raio da roda e 1/4 do raio da coroa, então cada pedalada corresponde a um deslocamento de 1,5 m.
16) Se as rodas de uma bicicleta têm raio igual a 50 cm e se o raio da coroa é o dobro do raio da catraca, então um ciclista que realiza duas pedaladas por segundo nessa bicicleta movimenta-se a 4πm/s.
29-(UERJ-RJ)

Uma máquina possui duas engrenagens circulares, sendo a distância entre seus centros A e B igual
a 11 cm, como mostra o esquema: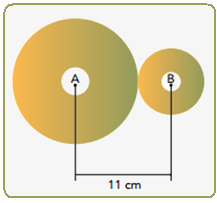
Sabe-se que a engrenagem menor dá 1000 voltas no mesmo tempo em que a maior dá 375 voltas, e que os comprimentos dos dentes de ambas têm valores desprezíveis.
A medida, em centímetros, do raio da engrenagem menor equivale a:
(A) 2,5
(B) 3,0
(C) 3,5
(D) 4,0
