Resolução do Movimento uniforme e encontro de móveis em MU

Movimento uniforme e encontro de móveis em MU

Resoluções

01- Colocando a origem da trajetória em Florianópolis e orientando a trajetória para a direita — equação horária — S = S_o + Vt — S= 0 + 60t — quando ele chega em Laguna
S=100km — 100=60t — t=5/3h=1h +2/3h=1h e 40min (tempo do percurso)

Chegou em Laguna às 13h e 30min + 1h e 40min — t=15h e 10min — R- A

02–

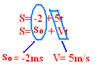
A velocidade escalar é positiva e portanto, o movimento é progressivo — R- C

03- a) O cronômetro foi acionado (t=0) quando ele passava pela posição (marco, espaço) 30m — S_o=30m — o movimento é retrógrado (move-se em sentido contrário ao dos marcos crescentes)

— V= – 5m/s

— S= S_o + Vt

— S=30 +(-5)t

— S=30 – 5t

b) Quando ele passa pela origem dos espaços,

S=0

— 0=30
– 5t — t=6s

04- a) S=10 – 2.6=10 – 12 — S= -2m

b) t=1s

— S₁=10 – 2.1 — S₁=8m

— t=4s

— S₄=10 – 2.4

— S₄=2m

— ΔS= S₄ – S₁=2 – 8= -6m

— ΔS= -6m

c) Origem – S=0 — 0=10 – 2t — t=5s

05-

a) V_m=(S₄ – S₂)/(t₄– t₂) = (1500 – 500)/(71,9 – 24,2)=1.000/47,7 — V_m=21m/s

b) Não, observe que ele percorre mesma distância 500m em intervalos de tempo diferentes.

06- S=S_o + Vt — 0=560 – 70t — t=8h

07- Fixando um ponto P no final do trem onde coloca-se a origem da trajetória que é orientada para a direita — na situação inicial

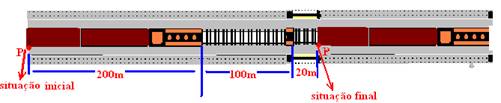
deduz-se a equação horária do ponto P e na situação final
S=320m

— inicial
– S=S_o + Vt
— S= 0 + 10t
— S= 10t

—final
– S=320m — 320=10t — t=32s — R- A

08- a) Como o tempo para o sinal ir de R até B é menor, o receptor R está mais próximo de B

Colocando a origem em R e orientando a trajetória de A para B

— equação do sinal RB

— S_RB=S_o + Vt= 0 + 3.10⁵.64,8.10^-3
— S_RB=205,5.10²km (distância de R até B)
— equação do sinal RA
— S_RA= S_o + Vt
— S_RA= 0 +(-3.10⁵.65,8.10^-3)

— S_RA=-194.10²km (distância de R até A, em módulo)
— S_RA + S_RB=2d
— 205,5.10² + 194.10²=2d
— d=399,90.10²/2
— d=200.10²km

b) d= x + S_RB
— 200.10²=x + 205,5.10²
— x=5,5.10²km=550km

c)

09- Para não haver colisão, a traseira do trem de cargas (ponto C) deve estar saindo do desvio quando a parte dianteira do trem de passageiros (ponto P) deve estar chegando ao desvio. Colocando a origem da trajetória no ponto P e orientando-a para a direita,

tem-se equação de P
— S_p=S_o + vt
— S_p=vt
— equação de C
— S_c=S_o + V_ct
— S_c= 650 – 10t

— tempo que C demora para chegar ao desvio, onde S_C=400m

— S_C=650 – 10t
— 400-650 – 10t
— t=25s
— Esse tempo deve ser o mesmo que P demora para chegar também ao desvio, ou seja, S_P=400m

— S_P=Vt
— 400=V.25
— V=16m/s

10- Colocando a origem da trajetória no ponto de onde a flecha é lançada e orientando-a para a direita

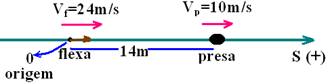
— equação da flexa
— S_f=S_o+ v_f.t
— S_f= 0 + 24t — S_f=24t

— equação da presa
— S_p=S_o + v_p.t
— S_p= 14 + 10t

— no encontro S_f=Sp
— 24t=14 + 10t
— 10=10t
— t=1s
— R- B

11- S_A=S_o + V_A.t
— S_A=0 + 74.t — S_B=S_o + V_B.t
— S_B=1.300 – 56.t — no encontro S_A = S_B
— 74t=1.300 – 56t — 130t=1.300 — t=10h — S_A =74t=74.10=740km
— R- B

12- Quando o carro de João chegou ao ponto P com velocidade de V_J=80km/h=80/60=4/3km/min, já fazia 4 minutos que o carro de seu amigo estava se movendo com V_a=60km/h=60/60km/min=1km/min e percorrido V_a=ΔS/ Δt — 1= ΔS/4 —
ΔS=4km —

Esta é a situação inicial, a partir da qual deduz-se a
equação horária de cada móvel

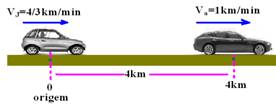
S_j=0 + 4/3t
— As=4 + 1.t — no encontro
— S_J= S_A
— 4/3t = 4 + t
— t=12min — R- C

13- 2 saltos do cão (s_c) equivalem a 5 saltos da lebre (s_l)
— 2.s_c=5.s_l
— s_c=2,5s_l
— velocidade do cão
— V_c=3s_c
— velocidade da lebre
— V_l=7s_l
— colocando a origem no cão e orientando a trajetória para a direita
— equação do cão
— S_c=0 + 3s_c.t

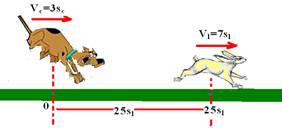
— equação da lebre
— S_l=25s_l + 7s_l.t
— no encontro
— S_c=S_l — 3s_c.t=25s_l + 7s_l.t
— t=50s_l
— substituindo t=50s_l em S_l=25s_l + 7s_l.t
— S_l=25s_l + 7s_l.(50s_l)
— S_l=375s_l (até o encontro a lebre deu 375 saltos) e o cão dará 375/2,5=150saltos
— R-E

14- Quando Pedro partiu, Alberto já estava na posição
— V_a = ΔS/ Δt
— 54 = ΔS/(i/60)
— ΔS=0,9km

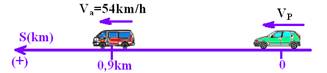
— situação inicial
— S_P=0 + V_P.t
— S_A= 0,9 + 54t
— no encontro S_A= S_P e t=3min=3/60=1/20h
— V_P.t= 0,9 + 54t
— V_P.1/20 = 0,9 + 54.1/20
— V_P=18 + 54
— V_P=72km/h
— R-C

15-
Quando o táxi saiu o ônibus estava na posição — 60=d/5/60 — d=5km

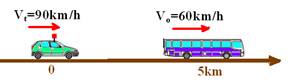
— situação inicial
— S_t=0 + 90t
— S_o=5 + 60t
— no encontro S_t = S_o
— 90t=5 + 60t
— t=5/30=1/6hX60=10min
— R – A

16- S_A=3 + 4t
— S_B=7 + 2t
— S_A=S_B
— 3 + 4t=7 + 2t
— t=2s
— S_A=3 + 4.2
— S_A=11cm
— R- C

17- Esquematizando a situação inicial

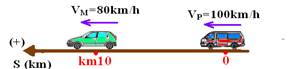
S_P= 0 + 100t
— S_M= 10 + 80t
— no encontro
— S_P = S_M
— 100t=10 + 80t
— t=0,5h
— S_P=100t=100.0,5=50km
— R- D

18- Considere P o ponto de encontro desses dois automóveis, e observe que do instante mostrado até o encontro, que ocorreu no ponto P, passaram-se 30 min ou 0,5 h, a distância percorrida pelo automóvel M vale — d_M=V_m.t=60×0,5 — d_M=30km — veja
figura

— nesse mesmo intervalo de tempo, o automóvel N percorreu
— d_N=50 – 30
— d_N=20km
— V_N=d_N/t=20/0,5
— V_N=40km/h
— R- A

19- A velocidade do foguete (v_f) é 4 vezes a velocidade do avião (v_a) — v_f = 4 v_a
— equacionando os dois movimentos uniformes,

uniformes, e colocando a origem no ponto onde está o foguete (instante t₁)
— S_f = v_f.t
— S_f = 4 v_a.t
— S_a = 4 + v_a.t
— no encontro eles ocupam a mesma posição no instante t₂
— S_f=S_a
— 4V_at₂=4 + V_at₂
— t₂=4/3V_a
— substituindo em S_f — S_f=4V_a.(4/3V_a)
— S_f=5,3km
— R- B

20- Do movimento uniforme — ΔS = v.Δt, sendo v é a velocidade da luz
— v = c
— ΔX=c.Δt

— antena 1
— X – X₁ = c(t – t₁)
— X = X₁ + c(t – t₁) (I)

— antena 2
— X – X₂ = -c(t – t₂)
— X = X₂– c(t – t₂) (II)

— somando I com II
— (I + II)
—X + X= [X₁ + c(t – t₁)] + [ X₂ – c(t – t₂)]
— 2X = X₁ + X₂ + c(t – t₁ – t + t₂)
— X = (X₁ + X₂ + c(t₂ – t₁))/2
— X=(X₁ + X₂)/2 + c(t₂ – t₁)/2

— subtraindo essas equações (I – II)
— X – X = [X₁ + c(t – t₁)] – [X₂ – c(t – t₂)]
— 0 = X₁ – X₂ + c(t – t₁ + t – t₂)
— 0 = X₁ – X₂ + 2ct + c(-t₁ – t₂)

— da figura dada
— X₁ = X₂ – L
— 0 = X₂ – L – X₂ + 2ct – c(t₁ + t₂)
— L + c(t₁ + t₂) = 2ct
— t=L/2c + (t₁ + t₂)/2

b) Para t₁ = T e t₂ = 2T, basta substituir esses valores nas equações encontradas para X e t
— X=(X₁ + X₂)/2 + c.(t₂ – t₁)/2
— X₂=X₁ + L
— X=(X₁ + X₂ + L)/2 + c.(T – 2T)/2
— X=X₁ + (L – cT)/2
— t=L/2c + (t₁ + t₂)/2
— t=L/2c + 3T/2

21- Observe que as fotos assinaladas são iguais.

Entre a primeira e a última foram tiradas 10 fotos (cuidado: a primeira não conta. Ela á o referencial)

— f=0,5Hz
— f=1/T
— 0,5=1/T
— T=Δt=2,0s
— V=ΔS/Δt=1,5.10/2
— V=7,5m/s
— R- B

22-Veja na figura a distância inicial entre eles
— d= 100 – 20=80m
— S_A = 20 + 3.t
— S_oA=20m
— V_A=3m/s (progressivo)

— S_B = 100 – 5.t
— S_oB=100m
— V_oB= – 5m/s (retrógrado)

— no encontro S_A = S_B
— 20 + 3t = 100 – 5t
— 8t = 80
— t=10s

— S_A = 20 + 3t=20 + 3.10=50m=S_B
— R- C.

 

Voltar para os Exercícios