Espelhos esféricos – Construção geométrica de imagens
Espelhos esféricos – Construção geométrica de imagens
Espelho esférico 
superfície esférica (calota) onde uma de suas superfícies é refletora.
Espelho esférico côncavo a superfície refletora é interna.
Espelho esférico convexo a superfície refletora é externa.
Representação simbólica dos espelhos esféricos
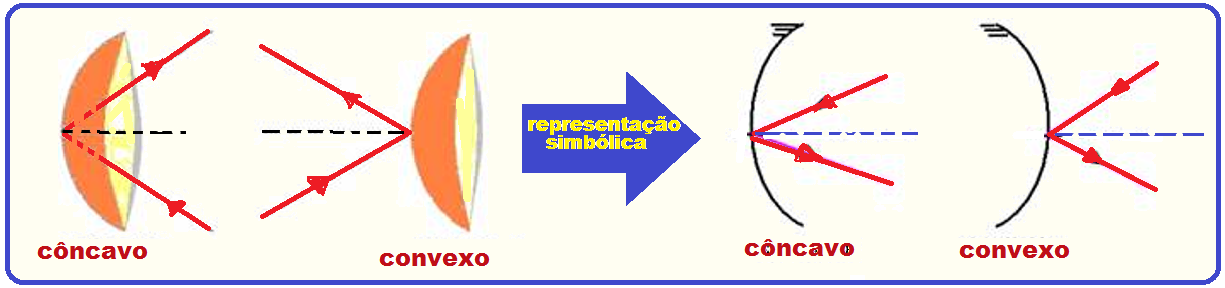
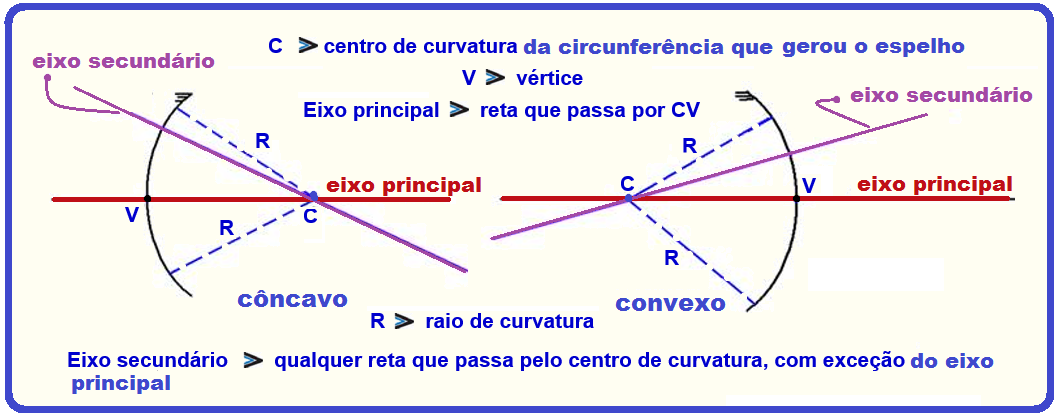
Elementos de um espelho esférico
Localizando o foco f de um espelho esférico
Para se localizar o foco F dos espelho deve-se considerar raios que incidam no espelho provenientes de um objeto situado no infinito, que incidem paralelamente ao eixo principal.
Estes raios são paralelos e, após se refletirem no espelho, retornam passando pelo foco.
Observe nas figuras abaixo, que o foco para espelho esférico côncavo é real, pois é obtido na
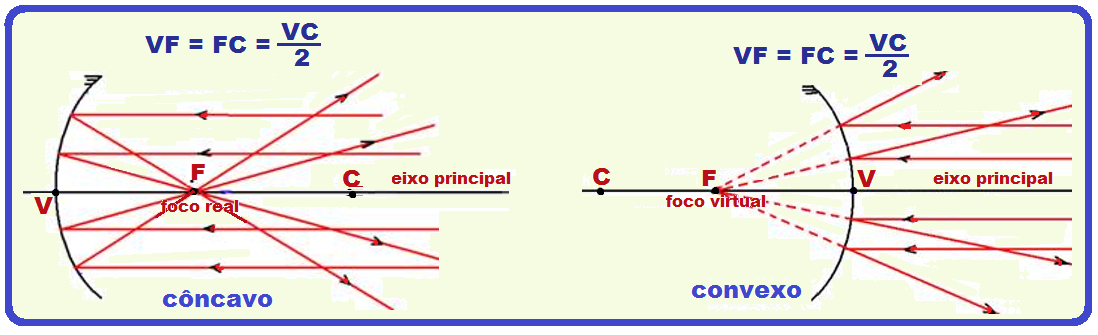
intersecção dos próprios raios luminosos refletidos sobre o eixo principal e, para o convexo é obtido na intersecção dos prolongamentos dos raios refletidos com o eixo principal, sendo, portanto, virtual.
Fisicamente o foco seria onde estaria localizada a imagem de um objeto situado no infinito.
A distância do foco principal F ao vértice V é chamada de distância focal f e f = R/2 ou R = 2f onde R é o raio de curvatura do espelho.
Condições de nitidez de Gauss
Condições de nitidez de Gauss para obtermos imagens aproximadamente perfeitas, isto é, nítidas, temos que verificar as condições de nitidez de Gauss que afirma: se os raios que incidirem nos espelhos esféricos não forem paralelos, pouco inclinados e próximos ao eixo principal, as imagens formadas não serão nítidas e é essa parte útil dos espelhos que será utilizada em todos nossos estudos.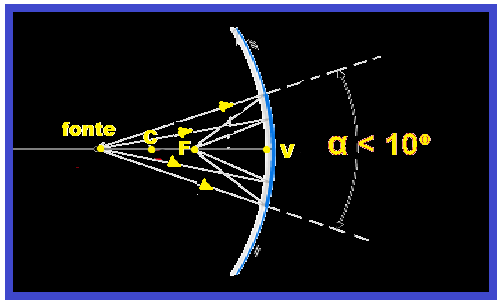
Essa parte realmente útil no espelho esférico de Gauss é uma pequena região da calota esférica em torno do vértice, ou seja, um espelho esférico de abertura bastante reduzida (a < 10o).
Raios notáveis
Podemos determinar a posição e o tamanho das imagens formadas pelos espelhos esféricos a partir do comportamento dos raios que saem do objeto e incidem o espelho.
Você deve memoriza-los pois serão úteis para a determinação das características das imagens formadas:
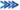Todo raio de luz que incide paralelamente ao eixo principal se reflete passando pelo foco
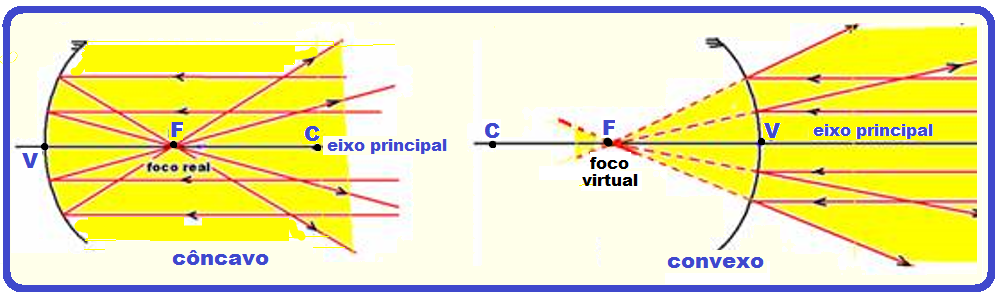
(espelho côncavo) ou de maneira que o prolongamento do raio refletido passa pelo foco (espelho convexo).
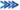Todo raio de luz que incide passando pelo foco (côncavo) ou de maneira que seu
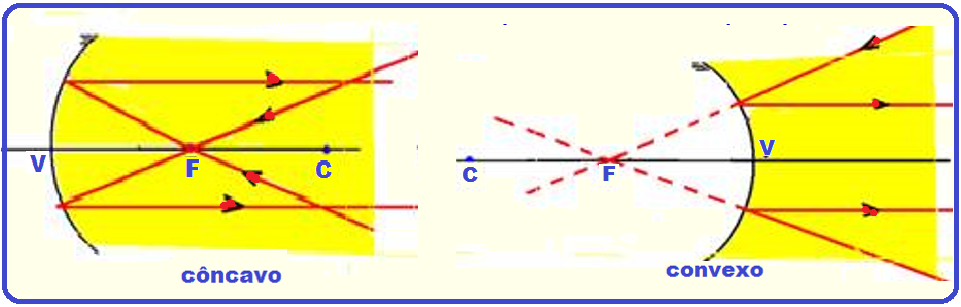
prolongamento passa pelo foco (convexo), se reflete paralelamente ao eixo principal.
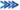Todo raio de luz que incide passando pelo centro de curvatura (côncavo) ou de maneira que seu
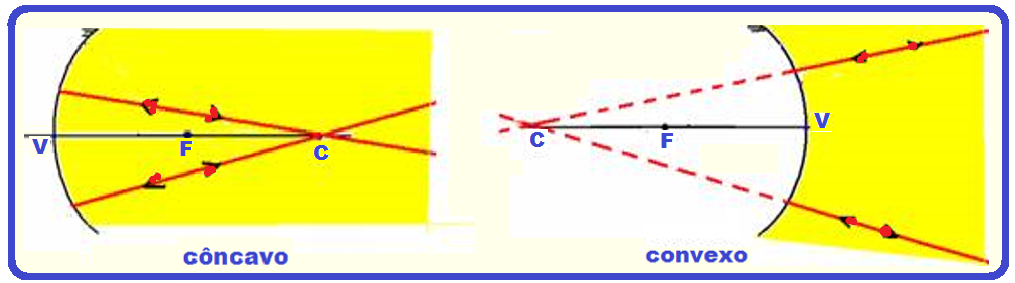
prolongamento passa pelo centro de curvatura (convexo) se reflete sobre ele mesmo.
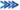Todo raio de luz que incide sobre o vértice V do espelho se reflete formando o mesmo ângulo
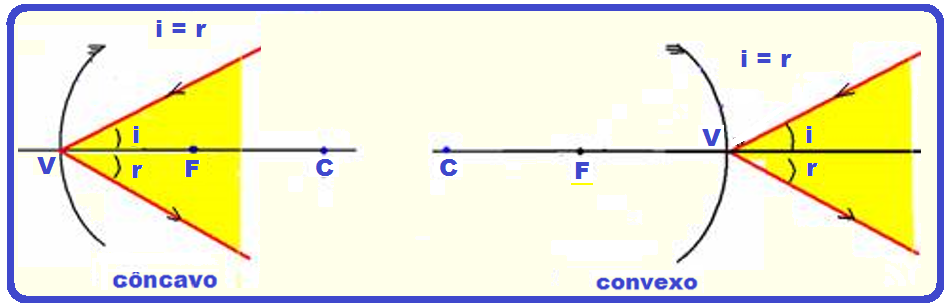
com o eixo principal
Construção geométrica de imagens nos espelhos esféricos côncavos
Espelho côncavo são 5 casos (em todos os casos estamos sempre utilizando o primeiro e o último dos raios notáveis acima).
1o caso Objeto antes do centro de curvatura C
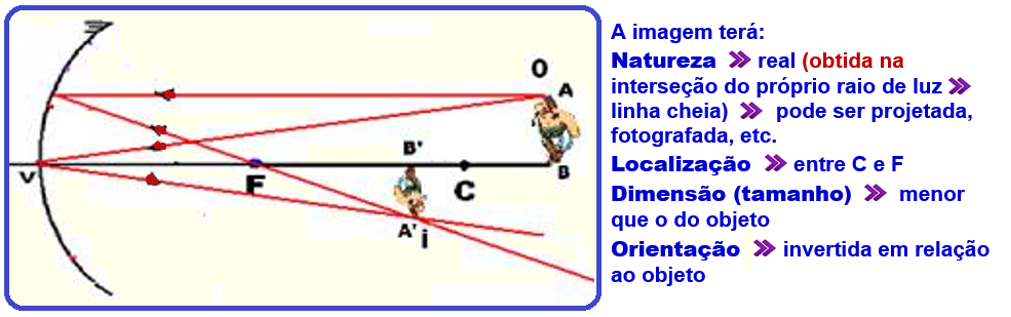
2o caso Objeto sobre o centro de curvatura C
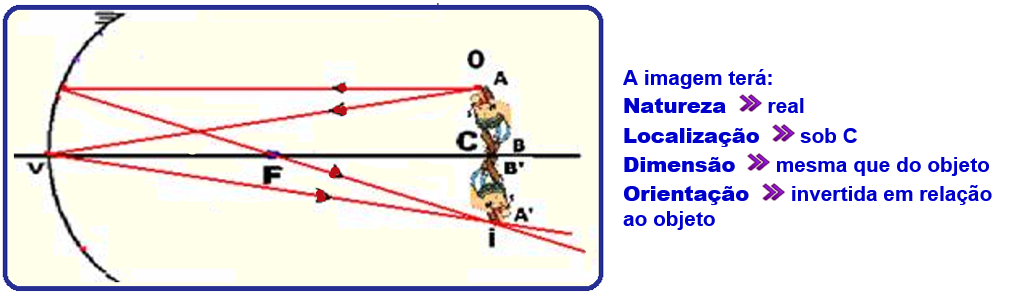
3o caso Objeto entre C e F
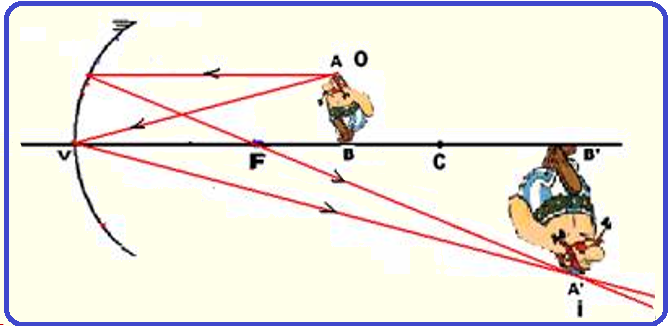
A imagem terá:
Natureza 
real
Localização antes de C
Tamanho maior que o do objeto
Orientação invertida em relação ao objeto
4o caso Objeto sobre o foco F
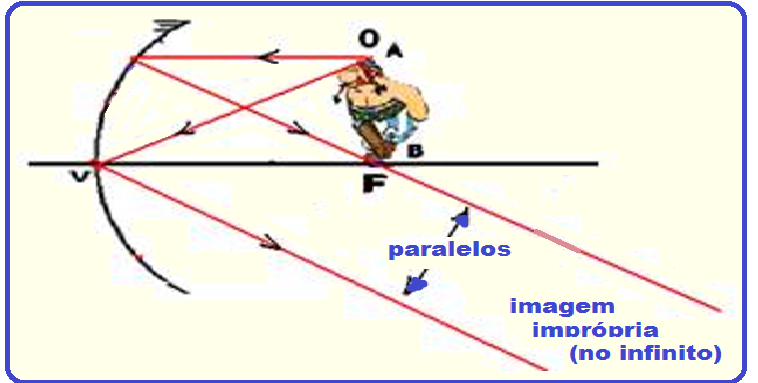
Fisicamente a imagem do objeto estaria localizada no infinito.
5o caso Objeto entre o foco F e o vértice V ou entre o foco F e o espelho
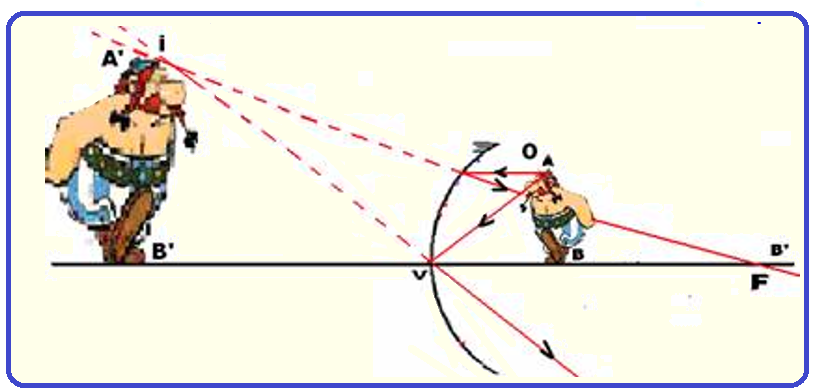
A imagem terá:
Natureza virtual (obtida na interseção do prolongamento dos raios de luz ) não pode ser projetada, fotografada, etc., atrás do espelho.
Localização atrás do espelho
Tamanho maior que o do objeto
Orientação direita em relação ao objeto
Utilidades: são empregados com freqüência quando se deseja obter uma imagem virtual e ampliada de um objeto, como é o caso dos espelhos de barbear, toalete, de dentista, espelho de otorrinolaringologia, etc.
Construção geométrica de imagens nos espelhos esféricos convexos
Espelho convexo Para qualquer localização do objeto
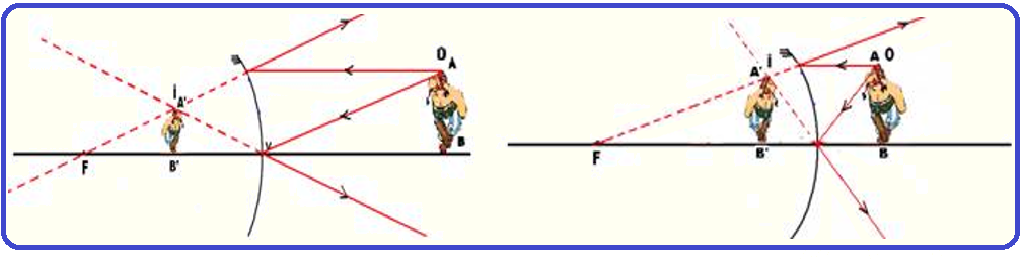
Independentemente da posição do objeto, a imagem terá sempre:
Natureza virtual
Localização atrás do espelho e entre V e F e observe nas figuras acima que à medida que o objeto se aproxima do espelho, a imagem também se aproxima e aumenta de tamanho, mas está sempre entre V e F.
Tamanho menor que o do objeto
Orientação direita em relação ao objeto
Utilidades: Os espelhos convexos são empregados como retrovisores em veículos, cabines de segurança, elevadores, etc.
Sua vantagem sobre o espelho plano, nesse particular, é ter maior campo visual. Têm, entretanto, o inconveniente de não darem noção da distância.
O que você deve saber, informações e dicas
Somente imagens reais podem ser projetadas em telas, fotografadas, filmadas etc.
Toda imagem virtual é direita e está localizada atrás do espelho.
Toda imagem real é invertida.
A imagem formada por espelho esférico convexo, para qualquer posição do objeto, é sempre virtual, direita, menor e está localizada atrás do espelho e entre V e F.
Os espelhos convexos são empregados como retrovisores em veículos, cabines de segurança, elevadores, etc. Sua vantagem sobre o espelho plano, nesse particular, é ter maior campo visual. Têm, entretanto, o inconveniente de não darem noção de distância porque diminuem o tamanho do objeto.
Os espelhos côncavos, quando o objeto está entre o foco e o espelho, são utilizados quando se deseja obter uma imagem direita e ampliada do objeto como nos espelhos de dentistas, de barbear, toalete, espelho de otorrinolaringologia, etc.
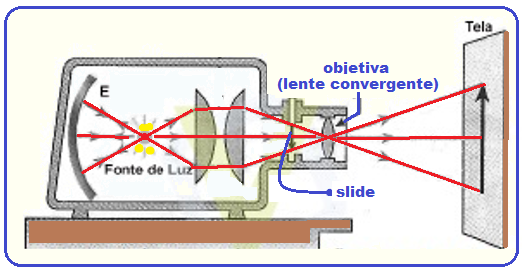
Nos projetores de slides utilizam-se espelhos côncavos esféricos. O filamento da lâmpada é colocado no centro de curvatura do espelho, formando-se na mesma posição uma imagem real do filamento antes do slide objeto; com isso, duplica-se a potência de iluminação propiciada pelo projetor, formando uma imagem projetada mais nítida na tela.
Como proceder para localizar o espelho esférico, seu foco e seu centro de curvatura sendo fornecidos o eixo principal e os tamanhos do objeto e da imagem
Baseado na figura abaixo onde são fornecidos o eixo principal (ep), os tamanhos e posições do objeto (O) e da respectiva imagem (i), pede-se localizar o espelho e seu tipo (côncavo ou convexo).
Observe que o espelho é côncavo porque espelhos convexos fornecem apenas imagens direitas.
Etapas:
Obter o ponto A’, simétrico a A e abaixo dele (mesmo tamanho da extremidade do objeto em relação ao eixo principal ep).
Unir A’ à extremidade de i e prolongar esta reta até ela interceptar o ep onde está o ponto que
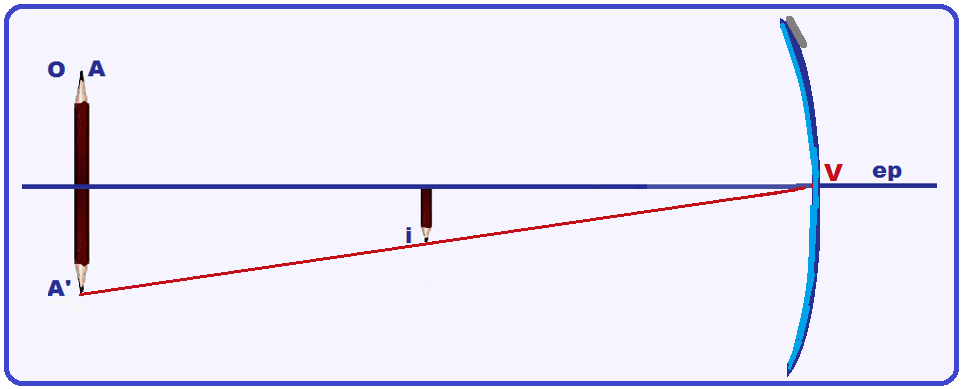
indica o vértice V do espelho que, como já vimos é côncavo e desenhá-lo.
Observe que esse procedimento foi baseado no seguinte raio notável: “Todo raio de luz que incide sobre o vértice V do espelho se reflete formando o mesmo ângulo com o eixo principal”.
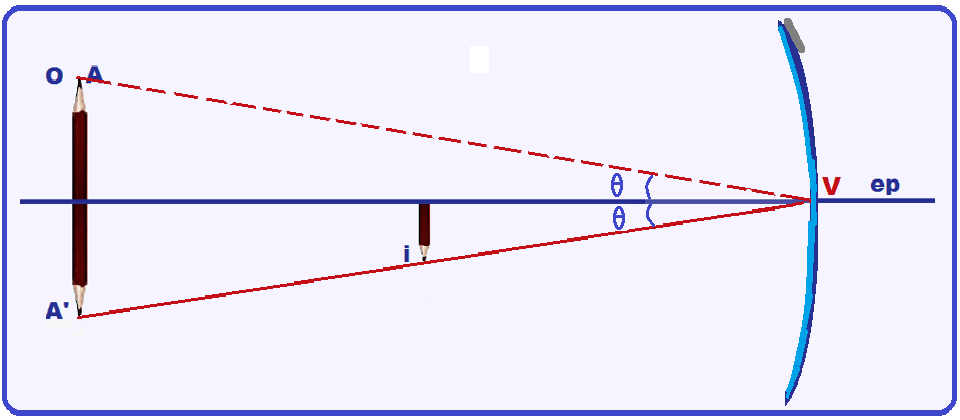
Assim, foi possível localizar o espelho conforme você pode observar na figura acima com a linha pontilhada.
Para localizar o foco você deve traçar um raio de luz que, partindo de A, incida no espelho
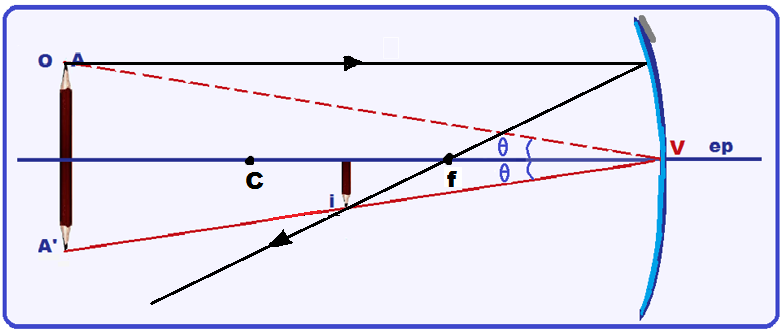
paralelamente ao eixo principal e retorne passando pelo foco F e que deve coincidir com a parte inferior da imagem i e, para localizar o centro de curvatura C você deve dobrar a distância FV.
Observe que este é o primeiro caso de espelho côncavo (objeto antes de C) que fornece imagem real, invertida, menor que a do objeto e localizada entre C e f.
Este processo é válido para qualquer tipo de espelho.
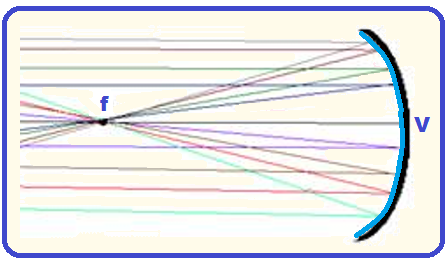
Quando espelhos côncavos recebem raios solares que chegam paralelos devido à enorme distância do Sol, o feixe, depois de refletido, se concentra no foco onde, por exemplo, podemos acender um cigarro.
A tocha olímpica é acesa por esse processo.
Localização da imagem de um objeto extenso no caso um triângulo Observe o objeto ABC da figura abaixo.
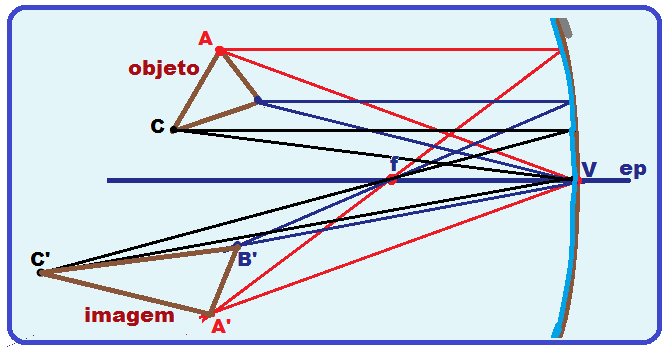
Sua imagem é obtida localizando a imagem por meio dois raios notáveis dos pontos A’, B’ e C’ e unindo-os.
Um holofote é constituído por dois espelhos côncavos E’ e E’’ de modo que que a quase totalidade da luz emitida por uma lâmpada L, seja projetada pelo espelho maior E’, formando um feixe de raios quase paralelos.
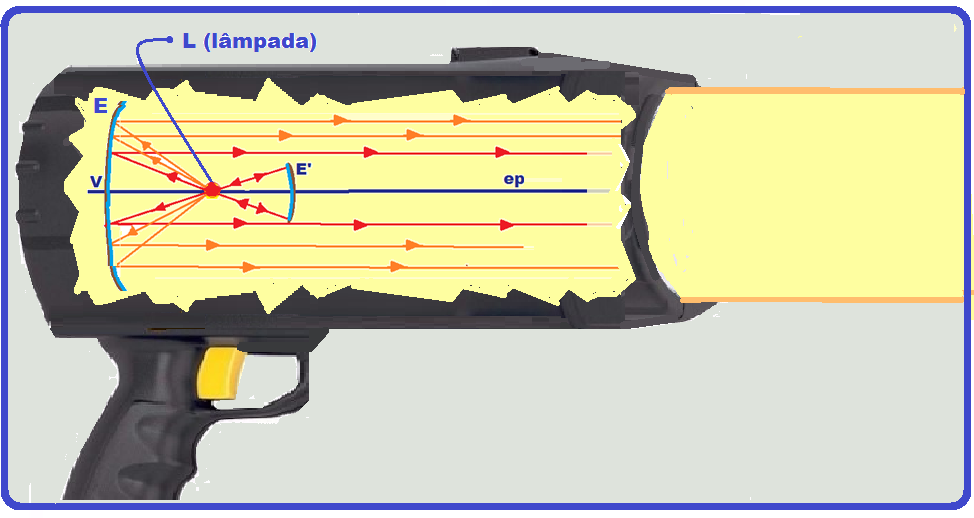
Para que os raios retornem paralelos a lâmpada L deve estar no foco de E’ (todo raio de luz que incide passando pelo foco retorna paralelamente ao eixo principal) e no centro de curvatura de E’’ ( todo raio de luz que incide passando pelo centro de curvatura retorna sobre ele mesmo).
Assim, todo raio de luz que emerge à esquerda de L e incide sobre E’’ retorna sobre si mesmo, passa pelo foco de E’ e retorna novamente de forma paralela.