Associação de Espelhos Planos
Associação de Espelhos Planos
Espelhos planos angulares
Vamos tomar dois espelhos planos E1 e E2 que formam entre si um angulo α para o qual estão voltadas as suas superfícies refletoras e colocar no interior desses espelhos um ponto objeto real P, luminoso ou iluminado.
Os raios de luz provenientes desse ponto sofrem reflexão regular, tanto no espelhos E1 como no E2, formando as respectivas imagens virtuais O1 e O2.
Por sua vez, os raios que se refletem em um dos espelhos, incidem no outro, cada ponto imagem funcionando como ponto objeto e, com isso, formando novas imagens virtuais.
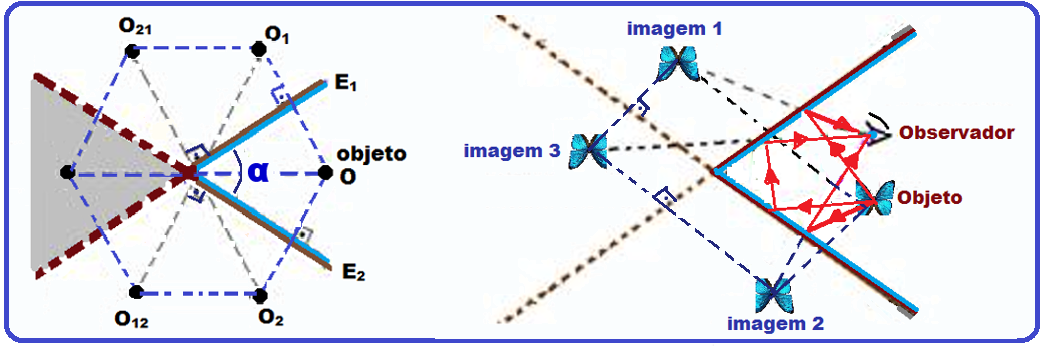
Essas várias reflexões ocorrem até que as imagens se formem atrás de ambas as superfícies refletoras e que não podem mais servir de objeto para os espelhos (parte hachurada da figura da esquerda acima).
Portanto, para cada ângulo a existe um número determinado de imagens.
Observe na figura da direita acima que, qualquer que seja a posição do observador e do objeto (ambos entre os espelhos) o observador sempre enxergará as imagens (neste exemplo 3 imagens, ângulo de 90o).
As imagens estão situadas numa mesma circunferência com centro no encontro dos dois espelhos.
Sendo n o número de imagens e α o ângulo entre os dois espelhos, a relação entre eles é fornecida pela expressão:
Esta equação só é válida em duas situações:
Se 360/α for par 
para qualquer posição do objeto entre os espelhos.
Se 360/α for ímpar o objeto deve estar exatamente no plano bissetor do ângulo formado entre os dois espelhos
O que você deve saber, informações e dicas
n corresponde à imagem de um único objeto
Se α = 90o 
n = (360/90) -1 = 3 imagens. Observe atentamente as figuras abaixo:
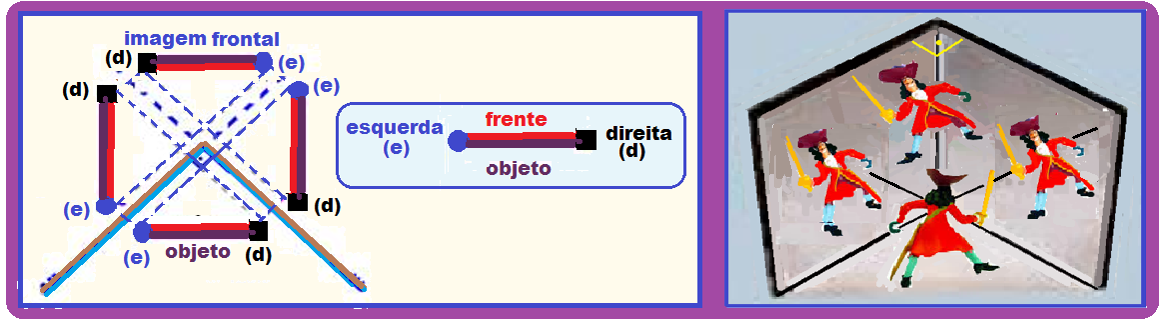
A imagem atrás do espelho corresponde à imagem das duas imagens.
Observe que a imagem frontal aos dois espelhos está de frente para o objeto e que objeto e imagem frontal não são reversos ou revertidos, ou seja, não trocam direita pela esquerda mas são direitos e não invertidos.
Assim, se o objeto for BOCA, a imagem frontal também será BOCA.
Observe também nas figuras abaixo que, dependendo da maneira como os espelhos formam ângulos
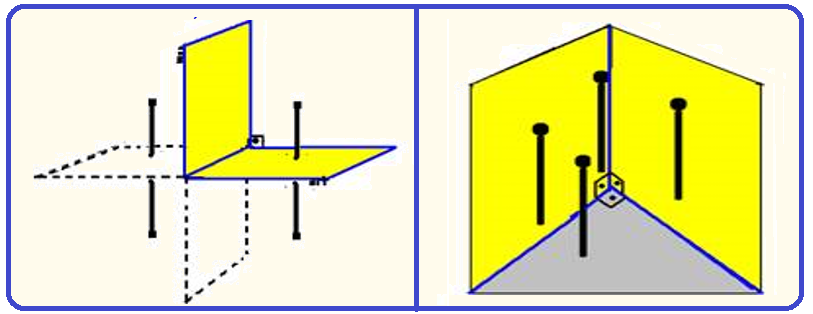
de 90o entre si, obtém-se imagens diferentes
Se α =180o, teremos 1 imagem (um único espelho).
Se α = 60o, teremos n = 360/60 – 1 n = 5 imagens (figuras abaixo).
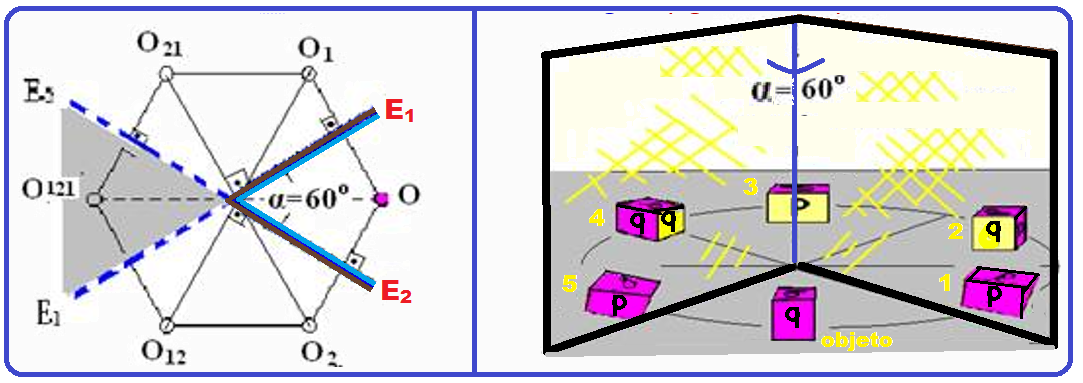
Na figura da direita acima todas as faces do cubo tem o símbolo
e a face que está voltada para o espelho tem cor amarela.
Observe que, das 5 imagens formadas, apenas nas 2, 3 e 4 aparecem a face voltada para o espelho e apenas nas 2 e 4 o símbolo está escrito corretamente.
Periscópio
Equipamento óptico, que permite observar um objeto ou conjunto de objetos por cima de obstáculos que impedem sua visão direta.
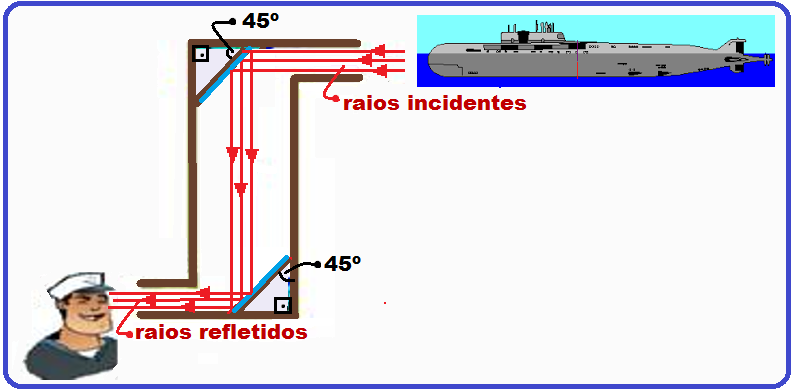
O raio de luz emitido pelo objeto reflete no 1o espelho, atinge o 2o e, após se refletir nele atinge o olho do observador, fazendo com que ele enxergue objetos que não estão ao nível de seu olho.
Esses dois espelhos planos que constituem o periscópio fornecem, a partir da luz proveniente de um objeto real, uma imagem final P’’ virtual, do mesmo tamanho do objeto e não reversa (não troca direita pela esquerda) e nem invertida (não troca cima por baixo).
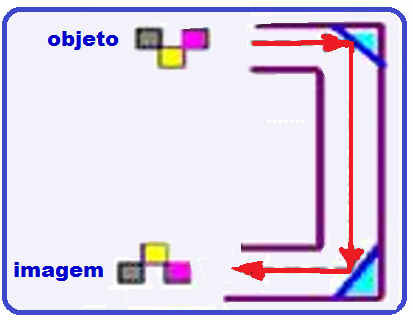
Já no sistema óptico ao lado, não se trata de um periscópio e a imagem final conjugada é invertida
(troca cima por baixo) e reversa (troca direita pela esquerda), mas mantém as mesmas dimensões do objeto.
Espelhos planos paralelos
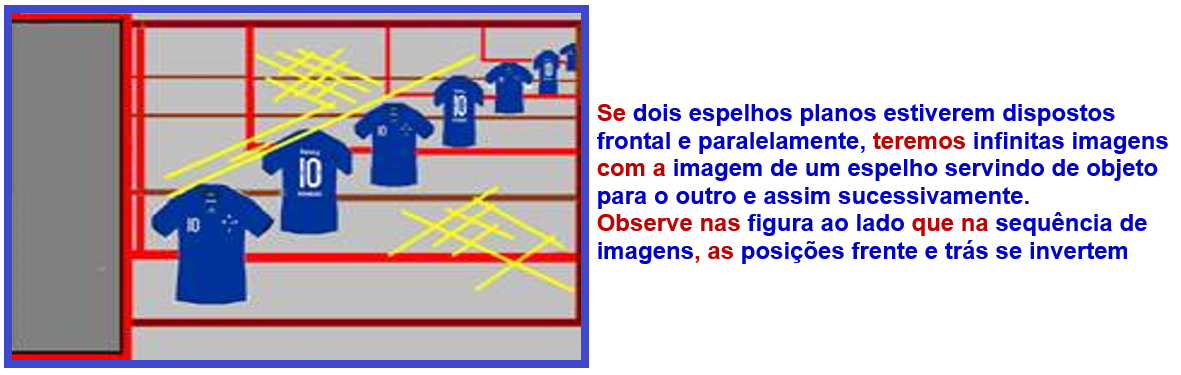
Observe atentamente a sequência de imagens da figura baixo e analise, procurando entender as
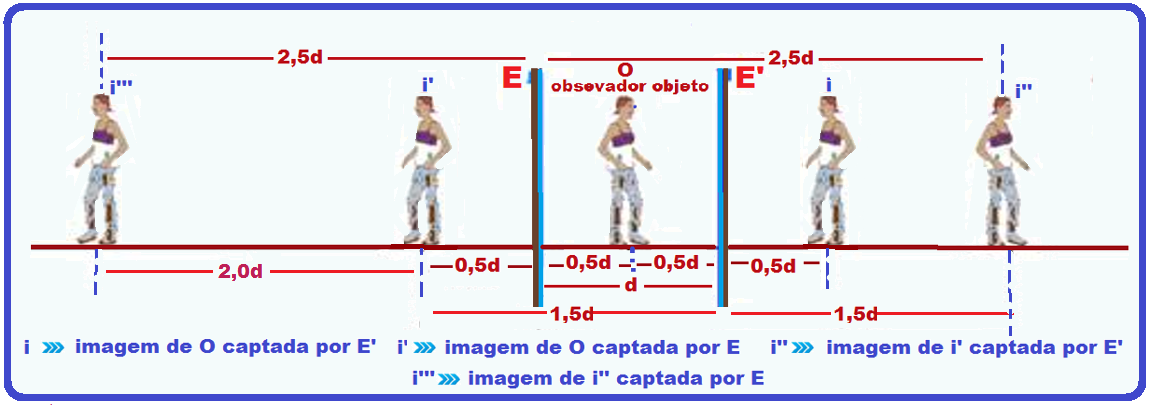
distâncias fornecidas entre os espelhos e as respectivas imagens.
Lembre-se de que o observador objeto enxerga apenas as imagens que estão à sua direita (sentido de seus olhos)
Quando uma foto de um casal é tirada entre dois espelhos planos verticais que formam um ângulo de 60o entre si, a quantidade de indivíduos que aparecem na chapa é de 12 pessoas.
Isso ocorre porque a expressão n = 360/α – 1 só é válida para um objeto.
Assim, para um objeto o número de imagens será n=360/60 – 1 n = 5 imagens de um único objeto.
Como temos 2 indivíduos aparecerão 10 imagens + os 2 objetos na foto aparecem 12 indivíduos.
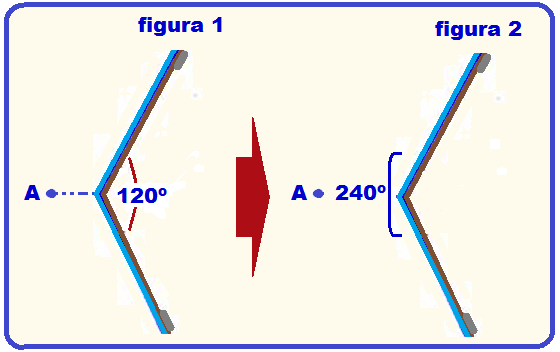
Se dois espelhos planos verticais formam um ângulo de 120o entre as duas superfícies não espelhadas conforme a figura (1) e um observador se encontrar no ponto A, quantas imagens completas de si mesmo ele verá?
Observe que o ângulo entre os dois espelhos planos é α = 360 – 120 = 240o e que o ponto A está no plano bissetor (figura 2) n = 360/α – 1 n = 360/240 – 1 = 1,5 – 1 = 0,5, ou seja, nenhuma imagem.
Ou ainda, observe nas figuras abaixo que o observador que está no ponto A está fora de seu campo
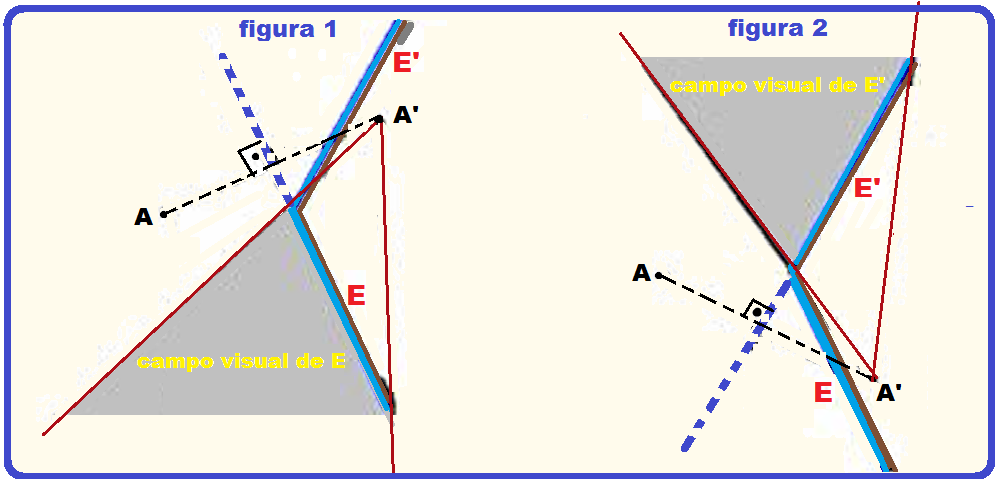
visual no espelho E’ (figura 1) e também no espelho E (figura 2).
Localização geométrica da imagem de um objeto vista através de um periscópio
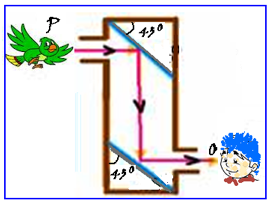
Uma criança observa um passarinho com um periscópio composto de dois espelhos planos E, paralelos e inclinados de 45o (figura).
O representa o olho da criança e o ponto P, o passarinho.
Localize a imagem do passarinho vista pela criança por meio desse periscópio.
Observe as figuras abaixo onde a primeira imagem P’ (conjugada pelo espelho E) funciona como objeto para o espelho E’, originando a imagem P’’, que é vista pelo observador (figura da esquerda) e
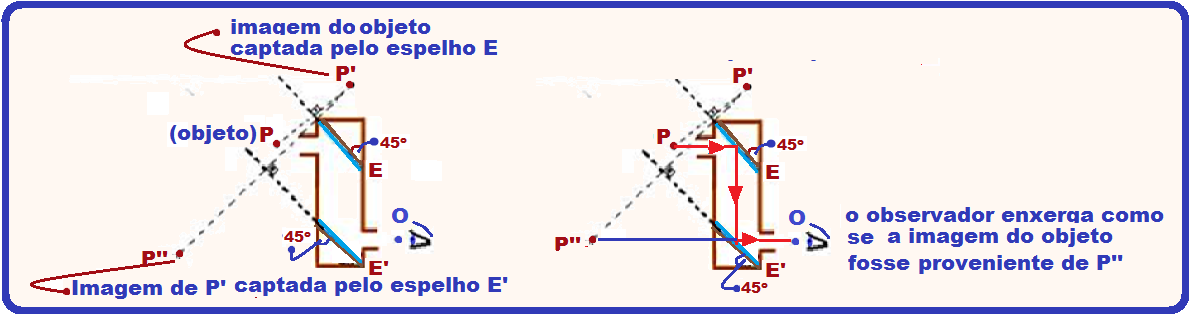
os raios de luz que possibilitam essa visualização estão na figura da direita.
Esses dois espelhos planos que constituem o periscópio fornecem, a partir da luz proveniente de um objeto real (no caso, o passarinho), uma imagem final P’’ virtual, do mesmo tamanho do objeto e não reversa (não troca direita pela esquerda).
Questão interessante:
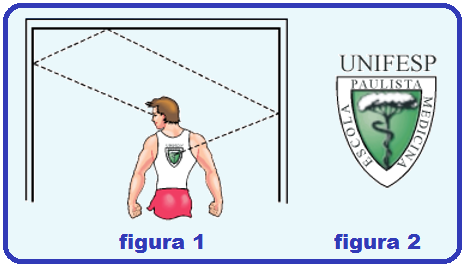
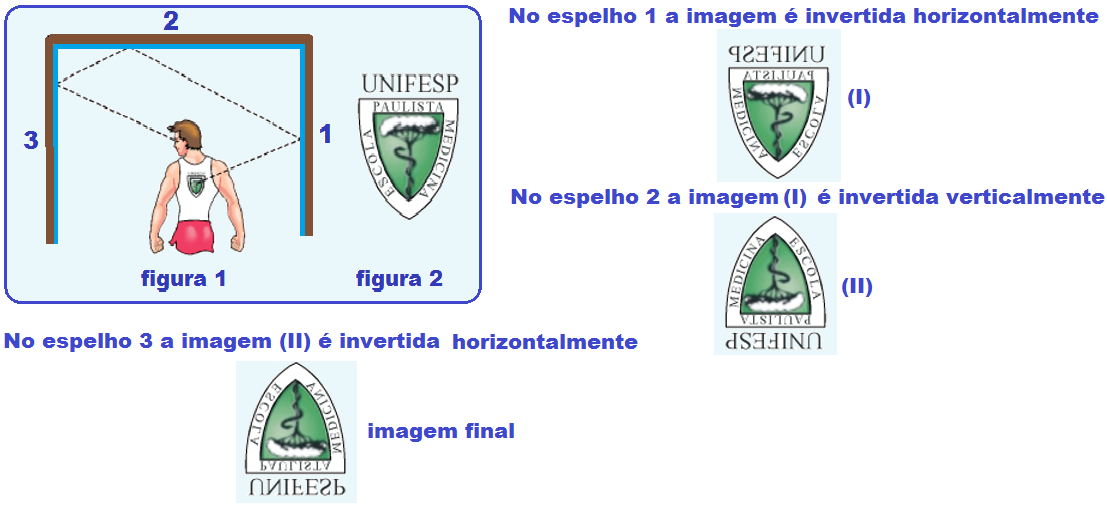
Numa sala, onde foram colocados espelhos planos em duas paredes opostas e no teto, um rapaz observa a imagem do desenho impresso nas costas da sua camisa.
A figura 1 mostra a trajetória seguida por um raio de luz, do desenho ao rapaz, e a figura 2, o desenho impresso nas costas da camiseta.
Explique como será a imagem vista pelo rapaz.
Lembre-se de que os espelhos planos produzem imagens reversas ou seja, trocam direita pela esquerda em espelhos verticais (inversão horizontal) e trocam cima por baixo em espelhos horizontais (inversão vertical).
Assim, veja a sequência abaixo:
