Instrumentos Ópticos
Instrumentos Ópticos
Instrumentos de projeção
São aqueles cuja imagem formada é real, pois pode ser projetada sobre um filme, uma tela, um anteparo, etc.
I – Câmera fotográfica ou máquina fotográfica 
dispositivo utilizado para capturar imagens. Consiste básicamente de uma caixa com orifício no qual se encontram uma ou mais lentes convergentes (objetiva), por onde entram os raios de luz provenientes dos objetos que queremos
fotografar ou filmar e que produzem uma imagem real, menor e invertida sobre o filme (câmera comum) ou sobre um censor que armazena as imagens em cartões de memória (câmera digital).
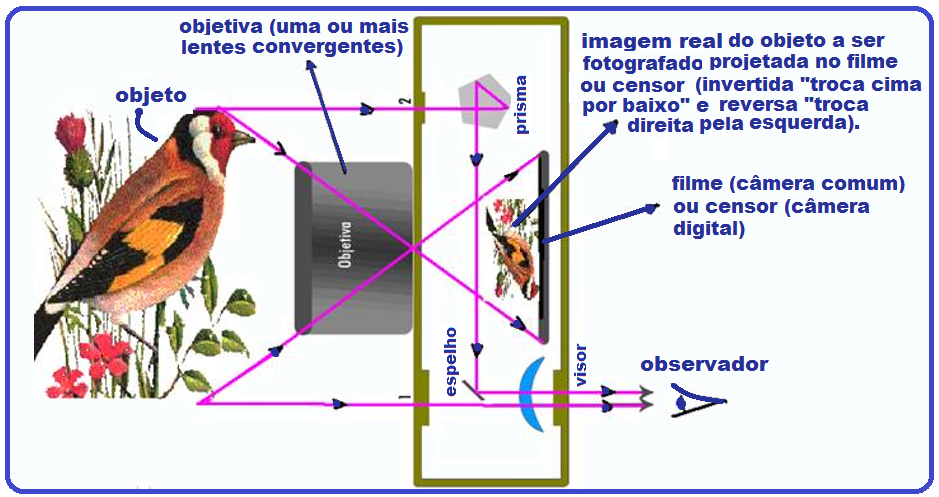Quando queremos focalizar a imagem devemos variar a distância lente-filme ou seja, variar a imagem P’ pois P e o foco são constantes.
Assim, quando o objeto se aproxima devemos afastar a lente para que a imagem seja projetada novamente sobrfe o filme.
II- Projetor consta de uma fonte de luz que, através de uma intensa iluminação e de uma lente convergente (ou um sistema de lentes), projeta a imagem de um objeto (filme, slide, transparência) em uma tela.
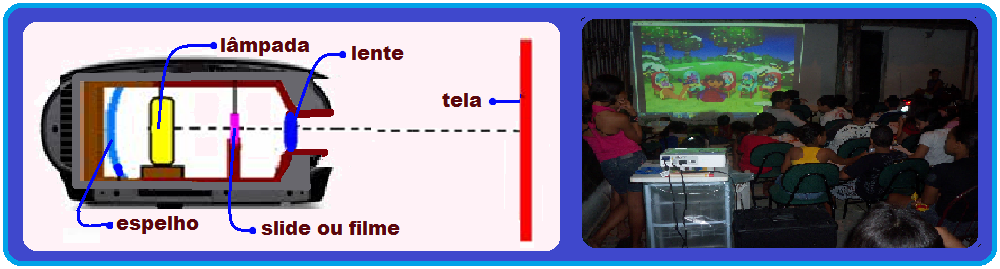
Essa imagem é real, invertida e maior, desde que o objeto esteja entre o centro de curvatura da lente e o foco objeto.
Instrumentos de observação
A imagem é observada diretamente pelo observador e é virtual e direita.
I-Lupa Também chamada de lente de aumento é uma simples lente convergente que fornece de um objeto colocado entre seu foco F e seu centro óptico O uma imagem virtual, direita e maior que o objeto observado.
Observe no esquema abaixo a formação da imagem A’B’ de um objeto AB em uma lupa, onde o objeto a ser observado tem que estar entre o foco objeto fo e a lente.
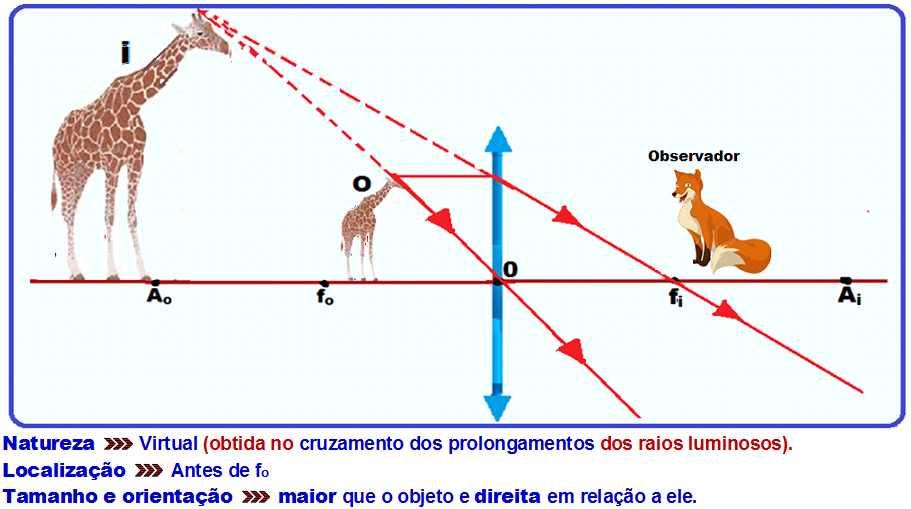
Sendo a imagem formada virtual, nas equações 1/f = 1/P + 1/P’, i/o = -P’/P e A = i/o = -P’/P, P’ deve e ser substituída com sinal negativo, pois P’< 0.
II- Microscópio composto Utilizado na observação de regiões de dimensões microscópicas que o olho humano não consegue perceber, como por exemplo, na histologia, anatomia, mineralogia, etc.
Consta de duas lentes convergentes (geralmente compostas) de pequenas distâncias focais que são: a objetiva (sistema de lentes bastante sofisticado) que está próxima ao objeto observado e a ocular (com no mínimo duas lentes) com a qual observamos a imagem fornecida pela objetiva.
Veja o esquema simplificado do microscópio composto.
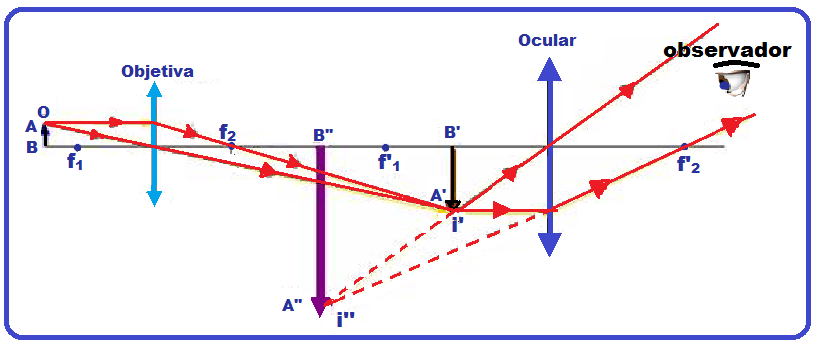
A distância focal da objetiva é muito pequena (milímetros). A objetiva forma do objeto AB uma imagem A’B’ real, invertida e maior que o objeto e essa imagem serve como objeto para a ocular (de distância focal da ordem de centímetros) que fornece uma imagem final A’’B’’, virtual, maior e direita em relação a A’B’.
Observe que A’’B’’ é direita em relação a A’B’ e invertida em relação ao objeto AB.
O aumento linear transversal do microscópio é fornecido pela expressão:
Amicroscópio = Aobjetiva . Aocular
O aumento produzido por esse microscópio chega até a 2000 vezes. Atualmente existem microscópios eletrônicos que produzem ampliações de até cem mil vezes.
III- Luneta astronômica utilizada na observação de astros ou de objetos distantes.
Consta de 2 lentes convergentes, a objetiva e a ocular. Ao contrário do microscópio composto, a distância focal da objetiva é muito grande (da ordem de metros). A ocular tem pequena distância focal.
Devido ao fato de o objeto estar muito afastado, a imagem (i1) formada pela objetiva está praticamente sobre seu foco (fobjetiva) e é real e invertida (veja figura).
Essa imagem (i1) vai servir como objeto para a ocular resultando numa imagem final (i2), virtual e invertida em relação ao objeto.
Observe que os focos da ocular (focular) e da objetiva (fobjetiva) estão muito próximos, praticamente coincidindo.
O aumento desta luneta é dado por A =fobj / foc. Observe por essa expressão que, para que o aumento seja bem grande, a distância focal da ocular deve ser bem menor que a da objetiva, ou seja, foc < fob.
No caso de uma luneta terrestre, onde a imagem final não é invertida devemos trocar a lente ocular convergente por uma lente divergente que tem distância focal negativa.
Como o aumento é dado por A = fobj / foc, é claro que maior será o aumento quanto maior o módulo da objetiva for maior que o módulo da ocular.
O que você deve saber, informações e dicas
Entender o funcionamento de todos os dispositivos descritos acima.
Se você quiser aprofundar mais, analise as resoluções dos exercícios a seguir:
01- Uma pequena luneta consiste em uma lente objetiva convergente de distância focal fob = 35 cm e de uma lente ocular divergente de distância focal foc = – 5,0 cm.
As duas lentes estão separadas por uma distância d = 30 cm, como ilustrado na figura 1.
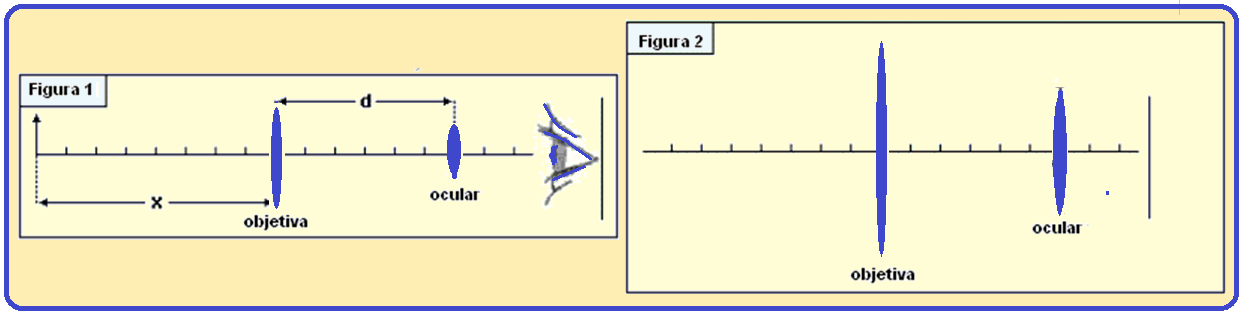
Um objeto é colocado sobre o eixo óptico da luneta, à esquerda da objetiva, distando x da mesma.
a) Calcule a posição da imagem final desse objeto, medida em relação ao centro da lente ocular, quando x = 40 cm.
b) Considere um feixe de raios paralelos de luz incidente na objetiva.
Complete o diagrama de raios, na figura 2, representando suas trajetórias no interior da luneta e indicando claramente a direção em que emergem da ocular (a figura foi ampliada na direção transversal ao eixo óptico da luneta para facilitar seu desenho)
Resolução:
a) Localizando a imagem P’ formada pela objetiva com o objeto P colocado à 40 cm da mesma tal que P = 4 0cm, sendo fornecida a distância focal da objetiva fobjetiva = 35 cm.
Aplicando a equação dos pontos conjugados P = 40 cm f = 35 cm 1/f = 1/P + 1/P’
1/35 = 1/40 + 1/P’ 1/35 – 1/40 = 1/P’ 1/P’ = (8 – 7)/280 P’ = 280cm (distância da objetiva até i1 conforme a figura abaixo com i1 localizada através dos dois raios notáveis traçados).
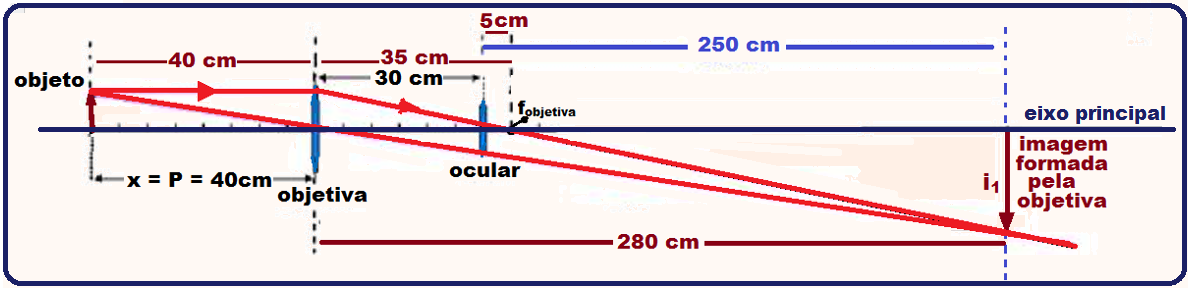
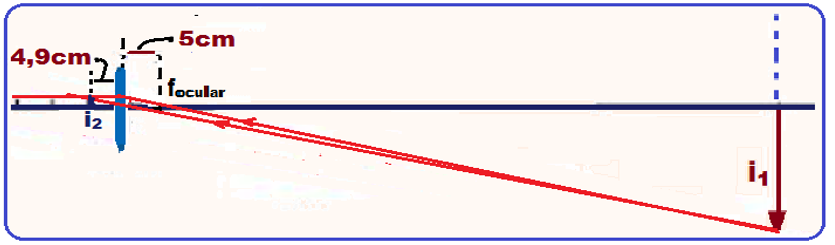
Localização da imagem i2 de i1, que funciona como objeto para a ocular sendo dados:
P = 250cm (distância do objeto i1 até a ocular) focular = – 5cm (divergente) equação dos pontos conjugados de Gauss 1/f = 1/P + 1/P’ 1/-5 = 1/250 + 1/P’ 1/P’ = – 1/5 – 1/250 1/P’ = (- 50 – 1)/250 P’= – 4,9cm (distância pedida de i2 até a ocular conforme a figura abaixo localizado por dois raios notáveis)
b) os raios que incidem paralelamente ao eixo da lente objetiva, emergem desta, em direção ao foco
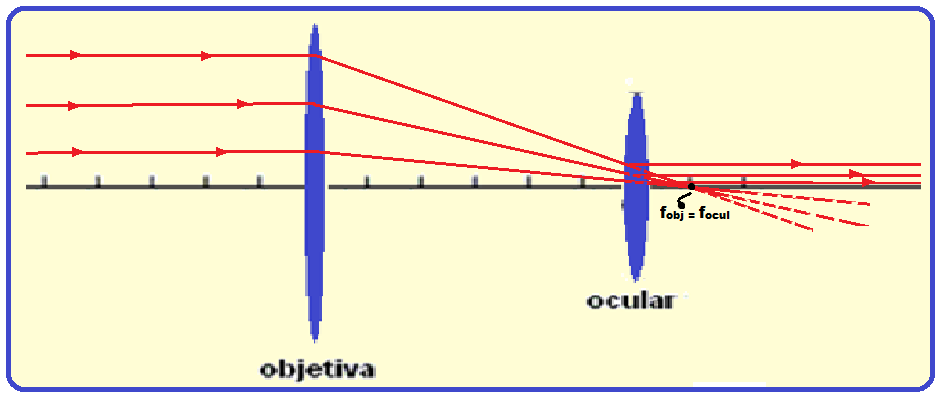
da lente ocular, emergindo da ocular, paralelamente ao eixo principal das lentes.
02- A figura a seguir é a representação esquemática de um sistema óptico formado por duas lentes convergentes, separadas por 50 cm.
As distâncias focais das lentes 1 e 2 são, respectivamente, 10 cm e 15 cm.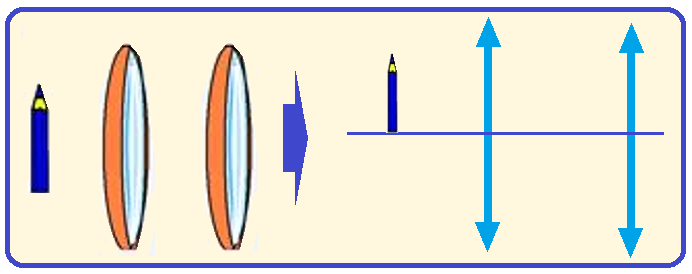
Utiliza-se um lápis com 4 cm de comprimento como objeto, o qual é posicionado a 15 cm da lente 1. Com base nesses dados:
a) Determine a posição da imagem formada pelo sistema de lentes.
b) Determine o tamanho da imagem formada pelo sistema. Ela é direita ou invertida, em relação ao objeto? Justifique sua resposta.
c) Empregando a representação de raios, faça um desenho em escala, mostrando a localização e o tamanho da imagem formada pelo sistema. Utilize a escala 10 para 1, ou seja, cada 10 cm no sistema real correspondem a 1 cm no seu desenho. (Cada quadrícula tem 0,5 cm de lado).
Resolução:
a) Dados distância focal da lente 1 (f1 = 10 cm) distância focal da lente 2 (f2 = 15 cm) distância entre as duas lentes (d = 50 cm) distância do objeto (lápis) à lente 1 (p1 = 15 cm).
Cálculo da distância (P1’) da primeira imagem à Lente 1 aplicando a equação dos pontos conjugados de Gauss 1/f = 1/P + 1/P’ 1/10 = 1/15 + 1/P1’ P1’= + 30cm (a primeira imagem é real e forma-se 30 cm à direita da Lente 1).
Essa primeira imagem funciona como objeto para a segunda lente sendo a distância entre as lentes é d = 50 cm, a distância (p2) da primeira imagem à lente 2 é p2 = d – P1’= 50 – 30 p2 =20 cm (distância da primeira imagem, agora objeto, para a lente 2).
Cálculo da distância (P2’) da imagem final à lente 2 de distância focal f2 = 15 cm 1/f2 = 1/P2 + 1/P’2
1/15 = 1/20 + 1/ P2’ P2’= + 60cm (a imagem final é real e se forma 60 cm à direita da lente 2 ou 110 cm à direita da Lente 1).
b) O aumento fornecido pelo sistema é o produto dos aumentos A = A1 x A2 A= P1’/P1 x P2’/P2 A = 30/15 x 60/20 A= +6 (a imagem final é direita e 6 vezes maior que o objeto).
Altura h’2 da imagem final em relação à altura h = 4 cm do objeto A=h’2/h 6 = h’2/4 h’2 = 24cm (a imagem final é real, tem comprimento 24 cm e é direita em relação ao objeto, pois o aumento linear transversal é positivo).
c) Escala dada [10 cm : 1 cm : 2 quadrículas] [5 cm : 1 cm : 1 quadrícula] observe que
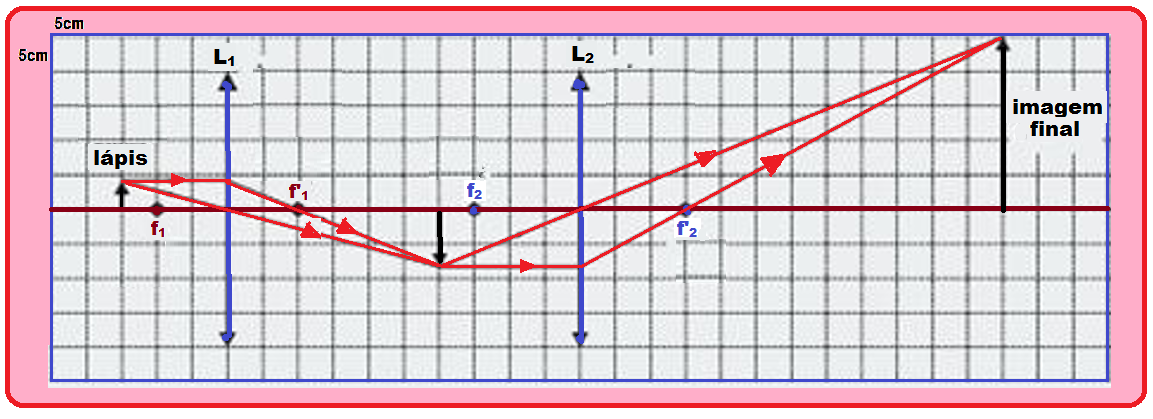
na figura acima, o lado de cada quadrícula representa 5 cm nas medidas dadas no enunciado.
03- Um microscópio composto é formado por duas lentes convergentes. A lente que fica mais próxima do objeto é a objetiva e aquela através da qual se observa a imagem é a ocular.
A imagem I1, formada pela objetiva, funciona como um objeto para a ocular (figura)
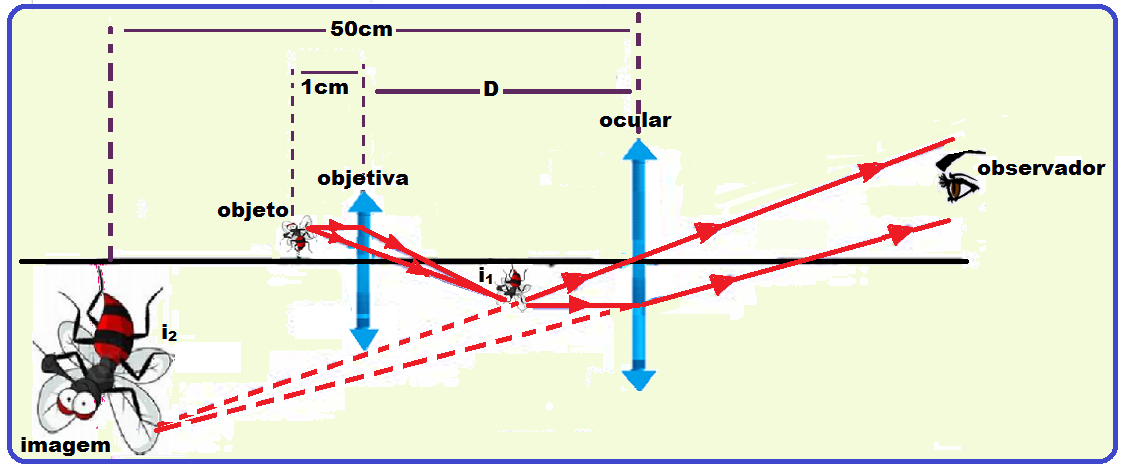
Quando o objeto é colocado a 1cm da objetiva a imagem final que se observa é 100 vezes maior que o objeto e se encontra a 50cm da lente ocular.
Se a ampliação devido à lente objetiva é 20 vezes, determine a distância D, em centímetros.
Resolução:
O aumento fornecido pela objetiva vale Aobjetiva = – 20 (negativo, a imagem é invertida).
Distância do objeto à objetiva P = 1 cm Aobjetiva = – P’/P -20 = – P’/1 P’ = 20 cm (distância da objetiva até a imagem por ela formada que é i1).
Afinal = Aobjetiva.Aocular -100 = – 20.Aocular Aoc = 5 (aumento fornecido pela ocular, positivo pois i2 é direita em relação à i1).
Imagem fornecida pela ocular dista 50cm da mesma e P’ é negativa pois a imagem é virtual) P’ = – 50cm Aocular = – P’/P 5 = – (- 50)/P P = 10cm (distância da ocular até i1).
A distância D pedida vale D = 20 + 10 D = 30cm.