Estudo Analítico das Lentes Esféricas
Estudo Analítico das Lentes Esféricas
Introdução
As lentes possuem dois focos, sendo, um ofoco principal objeto (fo) e o outro ofoco principal imagem (fi).
Ambos são simétricos e estão localizados sobre o eixo principal.
As posições e as alturas de objetos colocados diante de uma lente esférica são determinadas através das mesmas equações estudadas nos espelhos esféricos.
Seus sinais são fornecidos pelo referencial de Gauss.
Referencial de Gauss – Convenção de sinais
O sistema de eixo ortogonaistem origem no centro óptico da lente.
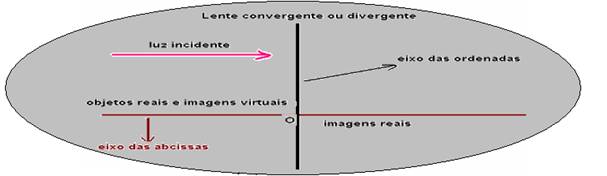
A origem do referencial está no centro óptico da lente.
O eixo das abscissas coincide com o eixo principal e tem sentido contrário ao da luz incidente para os objetos e a favor da luz incidente para as imagens.
Assim, observe na figura acima que imagens reais (à direita da lente) e objetos reais (à esquerda da lente) têm abscissas positivas e que imagens virtuais (à esquerda da lente) tem abscissas negativas.
O eixo das ordenadas é orientado para cima. Assim, a imagemie oobjeto O tem mesmo sinal se a imagem for direita em relação ao objeto e sinais opostos se a imagem for invertida em relação ao objeto.
Observe que a distância focal fé positiva para lentes convergentes e negativa para lentes divergentes.
Equação de Gauss
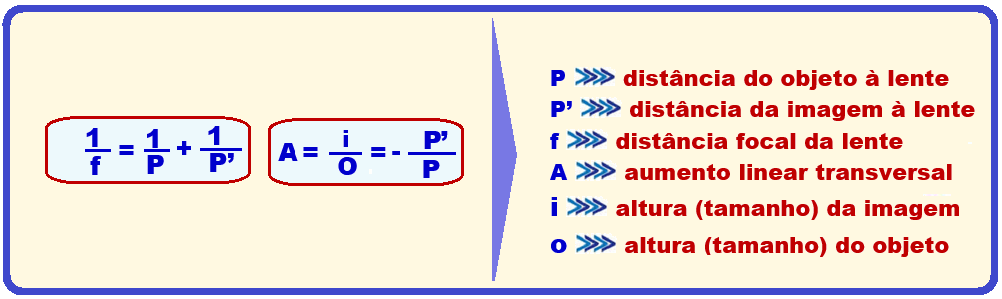
Vergência C de uma lente esférica
O que você deve saber, informações e dicas
Observe na expressão C=1/f que f e C são inversamente proporcionais, ou seja, lentes de pequenas distâncias focais, que provocam maiores alterações nas imagens dos objetos, têm maior vergência, na linguagem cotidiana “maior grau”.
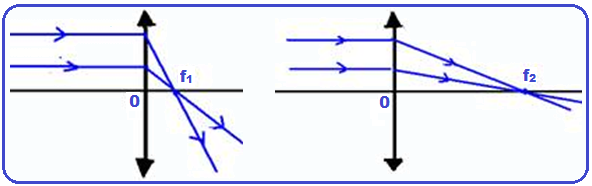
Note nas figuras que a vergência (grau) da lente da esquerda é maior que a da direita.
Questões interessantes nas quais você deve analisar atentamente os processos de resoluções:
01-(ITA-SP)
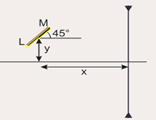
A figura mostra uma barra LM de 10√2cm de comprimento, formando um ângulo de 45° com a horizontal, tendo o seu centro situado a x = 30,0 cm de uma lente divergente, com distância focal igual a 20,0 cm, e a y = 10,0 cm acima do eixo ótico da mesma.
Determine o comprimento da imagem da barra e faça um desenho esquemático para mostrar a orientação da imagem.
Resolução:
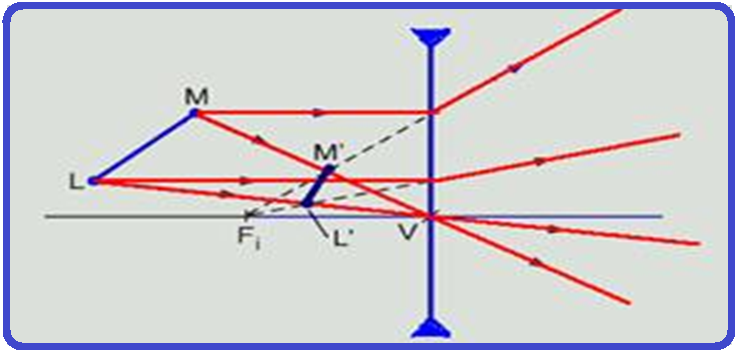
Determinação gráfica da imagem 
utilizando os dois raios notáveis da figura localizamos a imagem M’ do ponto M e a imagem L’ do ponto L unindo-os achamos a imagem L’M’ do objeto LM.
A figura mostra as coordenadas X e Y dos pontos M e L M(25;15) L(5;35):
Cálculo da coordenada P’ das imagens M’ e L’ pela equação dos pontos conjugados: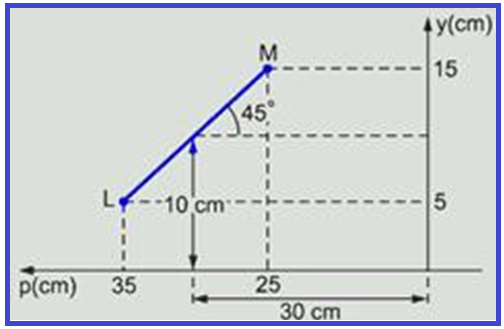
Coordenada da imagem de M 1/f = 1/PM + 1/ P’M 1/-20 = 1/25 + 1/P’M P’M = – 100/9 cm = – 11,1 cm (o sinal negativo significa que a imagem é virtual) em módulo P’M =11,1cm
M’x = 11,1 cm.
Coordenada da imagem de L 1/f = 1/PL + 1/ P’L 1/-20 = 1/35 + 1/P’L P’L= – 140/11 cm = – 12,7 cm em módulo P’L = L’x = 12,7 cm.
cálculo da coordenada Y’ das imagens M’ e L’ pela equação do aumento linear transversal
Y’L / YL= – P’L / PL Y’L/5= – ( – 140/11)/35 Y’L = 20/11 cm Y’L = 1,8 cm.
Y’M/YM= – P’M/PM Y’M/15 = – ( – 100/9)/25 Y’M = 20/3 cm = 6,7 cm.
coordenadas M’x e M’y do ponto M’(11,1;6,7)
coordenadas L’x e L’y do ponto L’(12,7;1,8)
Comprimento c da imagem da barra c2 = (P’M – P’L)2 + (Y’M – Y’L)2 c2 = { – 100/9 – ( – 140/11)}2 + (20/3 – 20/11)2 c2 ≈ 256.000/9.800 c2 ≈ 26 c ≈ 5,1cm.
02- Um objeto luminoso e uma tela de projeção estão separados pela distância D = 80 cm.
Existem duas posições em que uma lente convergente de distância focal f = 15 cm, colocada entre o objeto e a tela, produz uma imagem real na tela.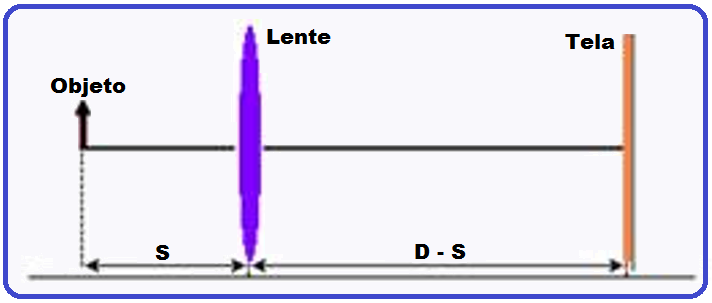 
Calcule a distância, em cm, entre estas duas posições.
Resoluções:
Observe a figura abaixo:
1/15 = 1/S + 1/ 80 – S) 1/15 = (80 – S) + S / S.(80 – S) 1200 = 80S – S2 S2 – 80S + 1200 = 0 Δ = B2– 4.A.C Δ = 40 S = – B ±√(Δ)/2.A S1 = (80 + 40)/2 S1 = 60 cm e P1’= 80 – 60 = 20cm S2 = (80 – 40)/2 S2 = 20cm e P2’ = 80 – 20 = 60cm.
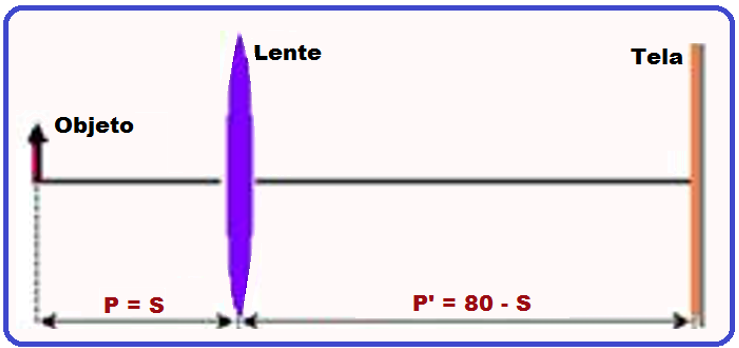
Portanto, para que a imagem seja real e nítida sobre a tela existe duas posições, uma a 20cm da lente e a outra a 40 cm da lente.
03- O sistema de imagens street view disponível na internet permite a visualização de vários lugares do mundo através de fotografias de alta definição, tomadas em 360 graus, no nível da rua.
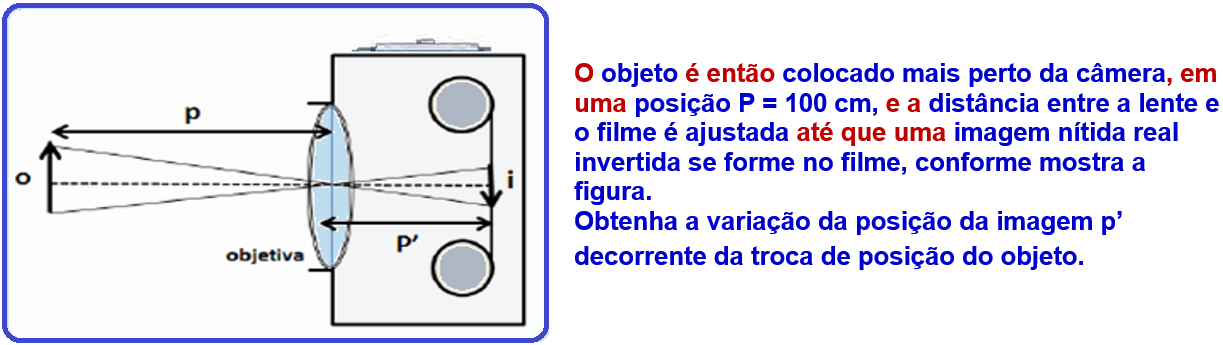
Em uma câmera fotográfica tradicional, a imagem é gravada em um filme fotográfico para posterior revelação.
A posição da lente é ajustada de modo a produzir a imagem no filme colocado na parte posterior da câmera.
Considere uma câmera para a qual um objeto muito distante fornece
uma imagem pontual no filme em uma posição P’ = 5 cm.
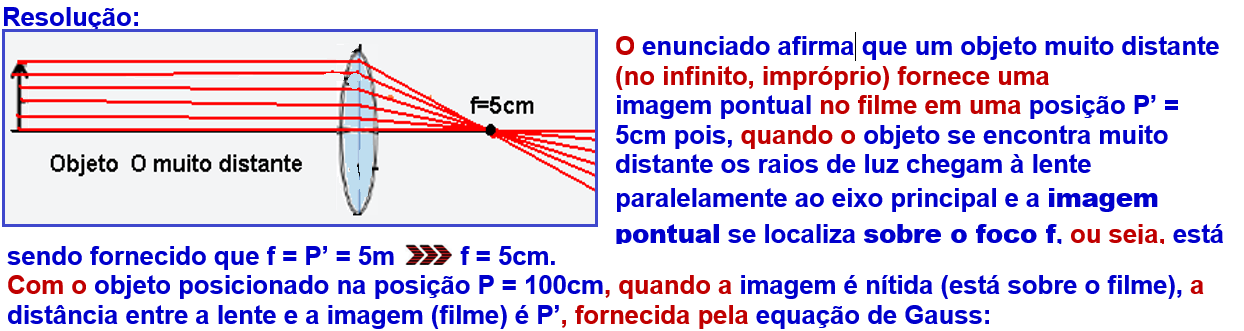
A variação da posição da imagem pedida devido à troca da posição do objeto vale ΔP’ = 5,26 – 5,0 ΔP’= 0,26cm.