Prismas

Prismas

Prisma óptico

Um prisma óptico corresponde a um conjunto formado por três meios homogêneos e transparentes

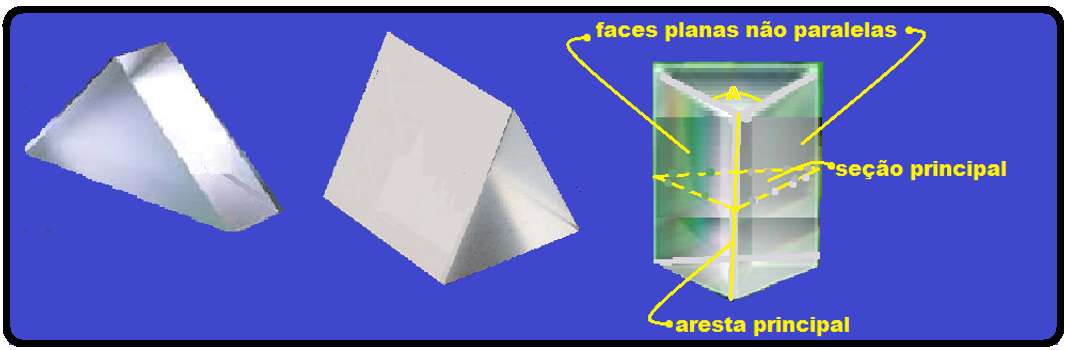
ou por dois dioptros planos, em que as superfícies planas não são paralelas (faces do prisma) que se interceptam em retas que são as arestas.

      

Tipos de prismas

Prismas dispersivos decompõem (dispersam) a luz policromática branca em suas infinitas

componentes monocromáticas (cores) que compõem o espectro luminoso.

   

Prismas refletivos (de reflexão total) substituem os espelhos, com melhor rendimento, na

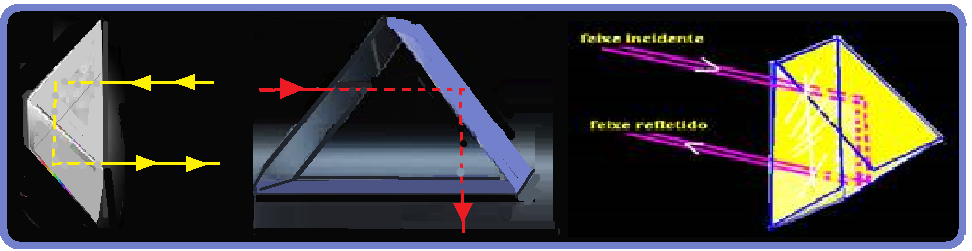
reflexão da luz.

Cálculo do desvio total ou desvio total angular (d)

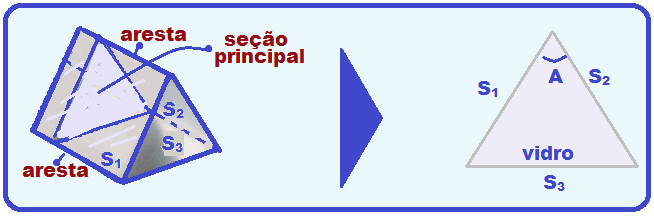
As superfícies S₁, S₂ e S₃ são as faces do prisma. A interseção das faces S₁ e S₂ determinam o ângulo A que é chamado de ângulo de refringência. 

A superfície S₃ que geralmente é opaca é utilizada apenas como apoio.

Considere o prisma da figura feito de material de índice de refração n₂ e imerso num meio de índice de refração n₁.

Um raio de luz monocromático incide na face da esquerda com ângulo de incidência i e se refrata no interior do prisma com ângulo de refração r.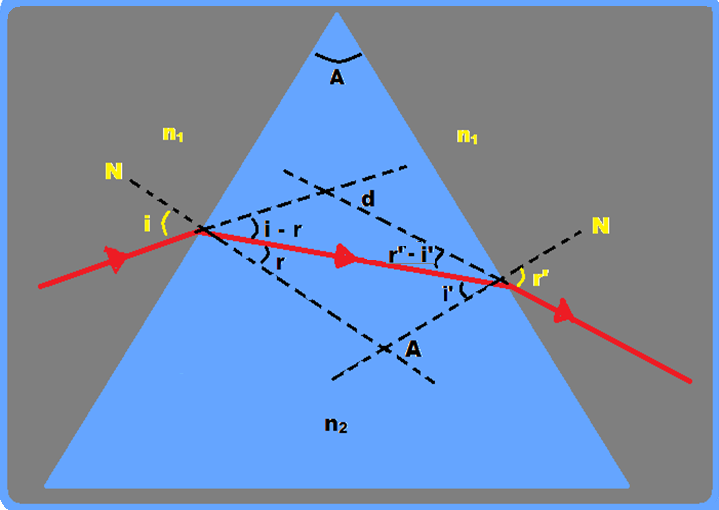

Aplicando a lei de Snell-Descartes na face da esquerda  n₁.sen i = n₂.sen r.

Esse raio incide na outra face com ângulo de incidência i’ e se refrata novamente para o meio 1 com ângulo de refração r’, tal que    n₂.sen i’ = n₁.sen r’.

O desvio total ou desvio angular (d) é definido como sendo o ângulo entre os prolongamentos dos raios incidente na 1^a face e emergente na 2^a face.

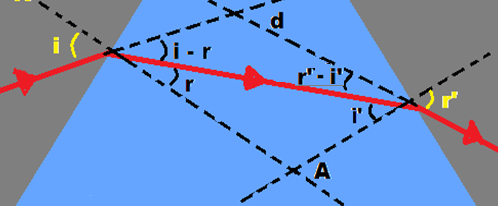
Observe na figura ao lado que o desvio angular na 1^a face (ângulo entre o prolongamento do raio

incidente e o do raio refratado) 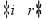, somado ao desvio angular na 2^a face ( ângulo entre o prolongamento do raio emergente e o raio incidente) 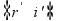nos fornece o desvio total d, ou seja, d = (i – r) + (r’- i’)  (I)

Observe ainda na mesma figura que o ângulo de refringência (A) do prisma é fornecido pela expressão A = r + i’    r = A – i’ (II)

Substituindo II em I obtemos a fórmula do desvio total:

 

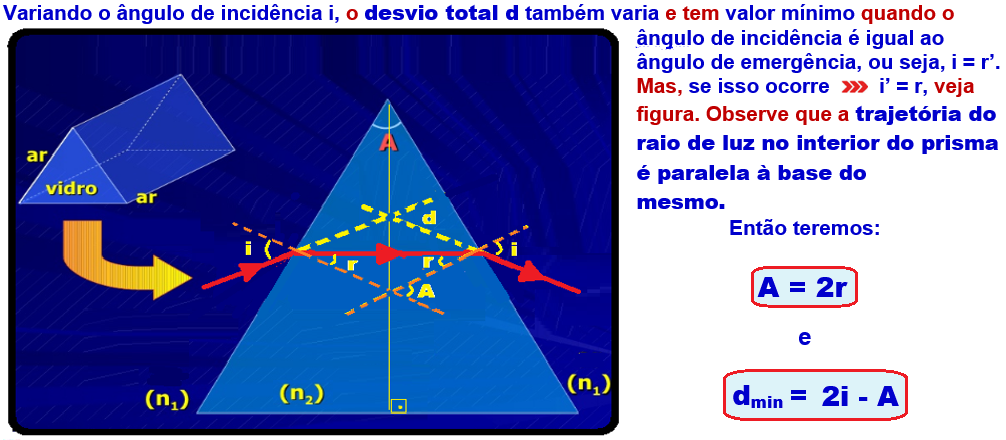
Desvio mínimo

Prismas de reflexão total

 Prismas de reflexão total  Quando a luz incide perpendicularmente à uma das faces de um prisma, ele pode sofrer refração sem sofrer desvio nesta face, reflexão total na segunda face e emergir na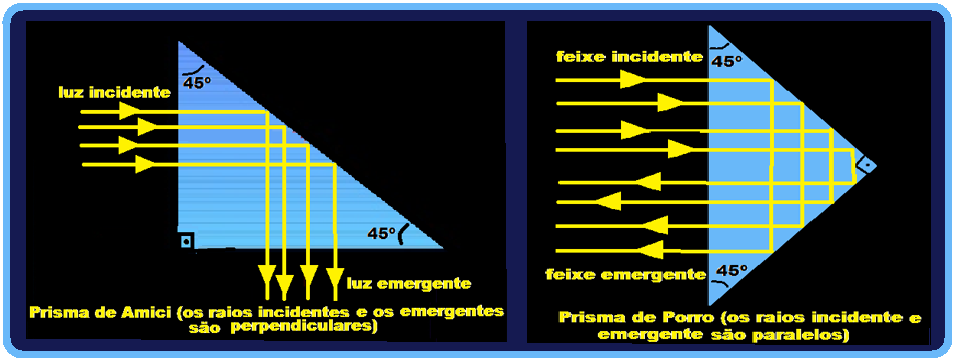

terceira face, também sem sofrer desvio.

Os prismas de reflexão total mais usados são constituídos de um triângulo retângulo isósceles, que recebem a luz em posições diferentes.

Normalmente são de vidro e imersos no ar, substituindo os espelhos planos com melhor rendimento.

 

O que você deve saber, informações e dicas

 

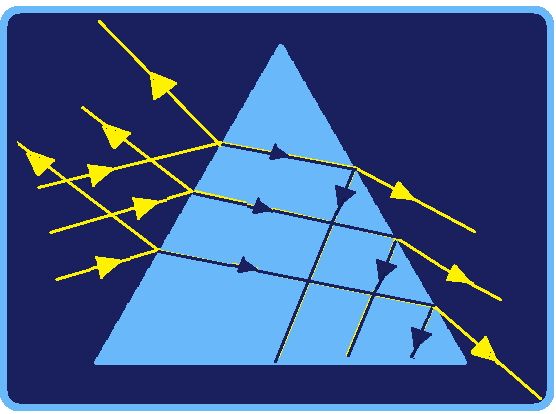
 Embora a refração seja predominante, ocorre também absorção e reflexão em ambas as faces do prisma.

As trajetórias dos raios incidente, do refratado no interior do prisma e do emergente se deslocam como se você estivesse girando um “saca-rolhas” no sentido horário, ou seja, o raio incidente sobe,

e os outros dois descem conforme a sequência das figuras acima.

Incidência normal na primeira face do prisma

 

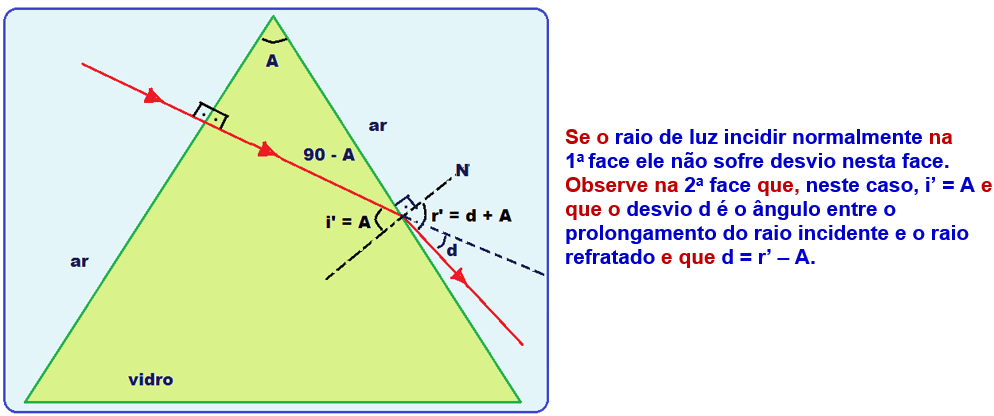
Ainda neste caso, se o raio emergir rasante, teremos que o ângulo de incidência i’ é igual ao ângulo

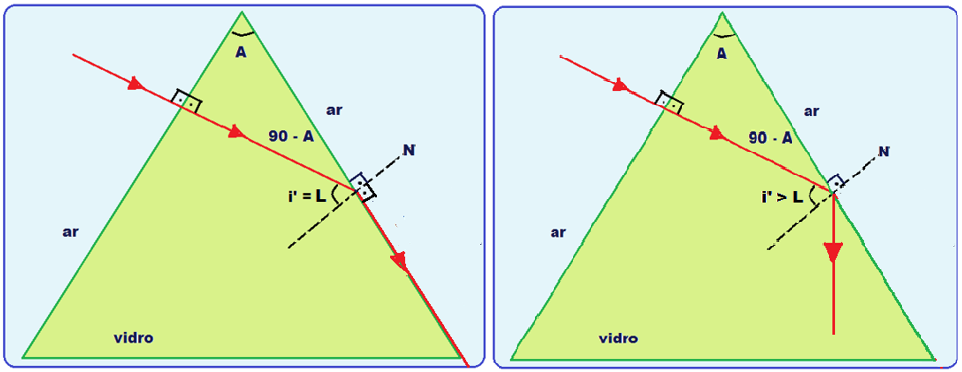
limite L, fornecido pela expressão senL = n_menor /n_maior    senL =n_ar/n   senL = 1/n.

Como i’ = L   sen i’ = sen L   sen i’ = 1/n . 

Portanto se sen i’ for igual a 1/n, o raio de luz emerge rasante e se, i’ for maior que L, o raio de luz sofre reflexão total pois neste caso sen L > 1/n .

 

 Se qualquer um dos dois prismas de reflexão total abaixo tiver índice de refração absoluto (n) e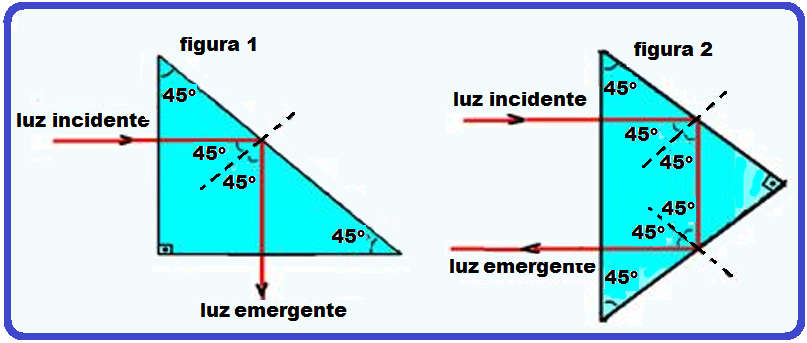

estiver imerso no ar (n_ar = 1), o valor do índice de refração n do prisma para que ocorra reflexão total na face interna (figura 1) ou faces internas (figura 2) deve incidir com ângulo superior ao ângulo limite, ou seja i > L, ou ainda seni > senL    sen 45^o > senL    √2/2 > 1/n   

n > √2 > 1,4.

Experiência de Newton na dispersão da luz policromática branca

Veja como Isaac Newton descreveu a proposta do experimento que lhe permitiu descartar a influência do vidro do prisma como causa da dispersão da luz branca.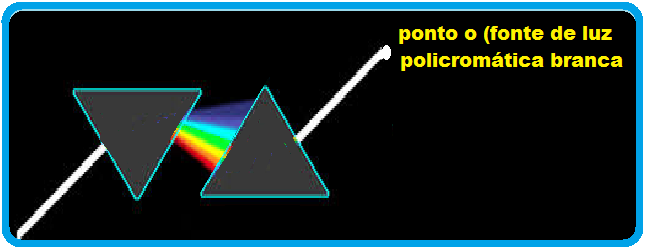

Considerando que a fonte de luz era o orifício O da janela do quarto de Newton, veja a descrição e o desenho da montagem executada por ele experiência:

“Eu peguei outro prisma igual ao primeiro e o coloquei de maneira que a luz fosse refratada de modos opostos ao passar através de ambos e, assim, ao final, voltaria a ser como era antes do primeiro prisma tê-la dispersado.”

Exercícios interessantes:

01-

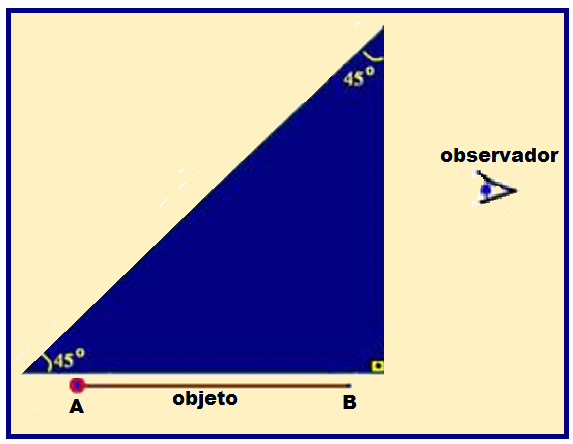
Na figura ao lado, estão representados um prisma retangular, cujos ângulos da base são iguais a 45^o, um objeto AB e o olho de um observador.

Devido ao fenômeno da reflexão total, os raios de luz provenientes do objeto são refletidos na base do prisma, que funciona como um espelho plano.

Esquematize a imagem A’B’ do objeto AB visto pelo observador:

 

Resolução:

Na figura o raio de luz vertical e para cima que sai de A penetra no prisma sem sofrer desvio, sofre

reflexão total na face interna inclinada e sai horizontalmente do prisma sem sofrer desvio e atinge os olhos do observador que vê a imagem A’ de A.

O mesmo processo é realizado pelo raio de luz que sai de B e atinge os olhos do observador que vê B’.

Unindo A’ com B’ você localiza a imagem A’B’ de AB vista pelo observador. 

02- Um tipo de sinalização utilizado em estradas e avenidas é o chamado olho-de-gato, o qual consiste na justaposição de vários prismas retos feitos de plásticos que refletem a luz incidente dos faróis dos automóveis.

a) Reproduza o prisma ABC representado na figura abaixo e desenhe a trajetória de um raio de luz que incide perpendicularmente sobre a face OG e sofre reflexões totais nas superfícies AC e BC.

Resolução:

a)

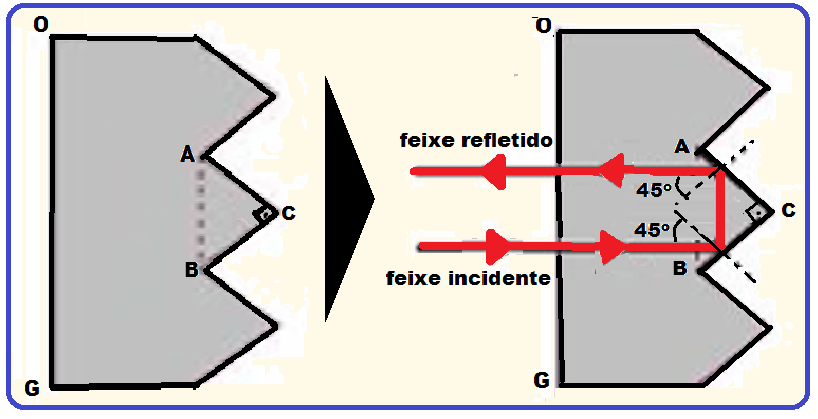
b) Determine o mínimo valor do índice de refração do plástico acima do qual o prisma funciona como um refletor perfeito de luz (toda luz que incide perpendicularmente à superfície OG é refletida). Considere o prisma no ar, onde o índice de refração vale 1,0.

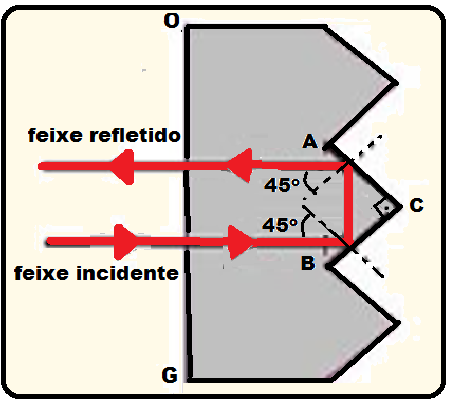
Para que haja reflexão total    i > L   seni > senL    sen45^o > senL    √2/2 > 1/n    n > √2.

03- Um raio monocromático de luz incide no ponto A de uma das faces de um prisma feito de vidro e imerso no ar.

A figura 1 representa apenas o raio incidente i e o raio refratado r num plano normal às faces do prisma, cujas arestas são representadas pelos pontos P, S e T, formando um triângulo eqüilátero.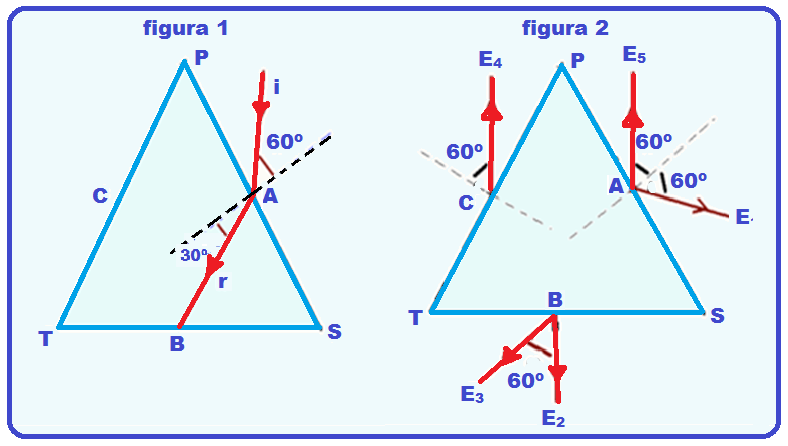

Os pontos A, B e C também formam um triângulo equilátero e são, respectivamente, equidistantes de P e S, S e T, e T e P. Considere os raios E₁, E₂, E₃, E₄ e E₅, que se afastam do prisma, representados na figura 2.

Podemos afirmar que os raios compatíveis com as reflexões e refrações sofridas pelo raio incidente, no prisma, são:

Resolução:

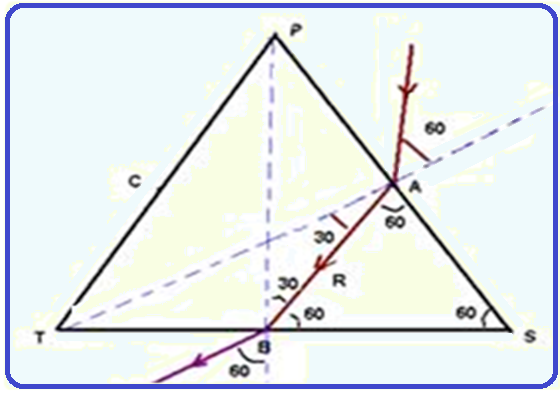
Refração no ponto A    n_ar.sen60^o = n_v.senr    1.√3/2 = n_v.sen30^o    1.√3/2 = n_v.1/2    n_v = √3 (índice de refração do vidro).

Quando atinge o ponto B o raio de luz sofre refração passando para o ar onde n_ar = 1, pois sen30^o = 1/2 e senL = n_menor/n_maior = 1/√3 = √3/3    assim, como seni < senL    i < L    ele não sofre reflexão total em B, sofrendo refração e passando para o ar. 

Aplicando Snell-Descartes no ponto B    n_v.sen30^o = n_ar.senr    √3.1/2 = 1.senr    senr =

√3/2    r = 60^o    R- A

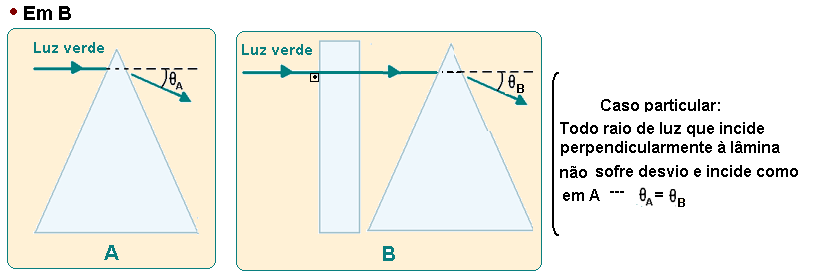
04- Um prisma triangular desvia um feixe de luz verde de um ângulo Ө_A, em relação à direção de incidência, como ilustra a figura A.

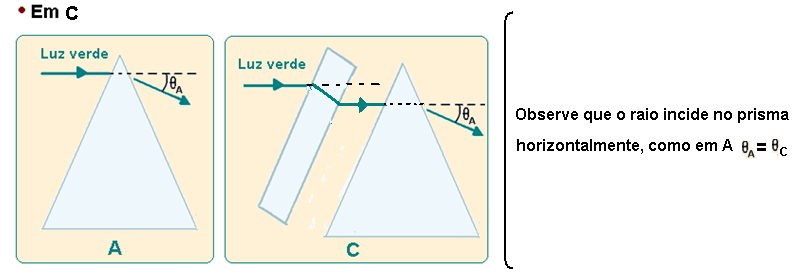
Se uma placa plana, do mesmo material do prisma, for colocada entre a fonte de luz e o prisma, nas posições mostradas nas figuras B e C, a luz, ao sair do prisma, será desviada, respectivamente,

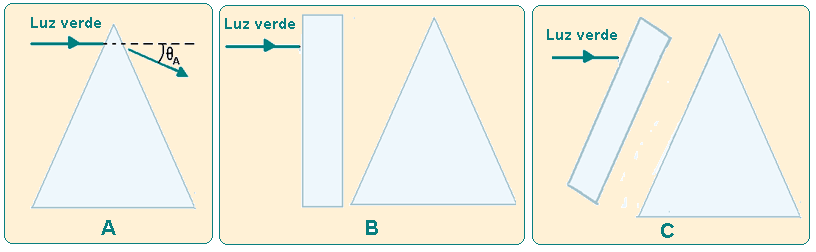de ângulos Ө_B e Ө_C, em relação à direção de incidência indicada pela seta.

Os desvios angulares serão tais que

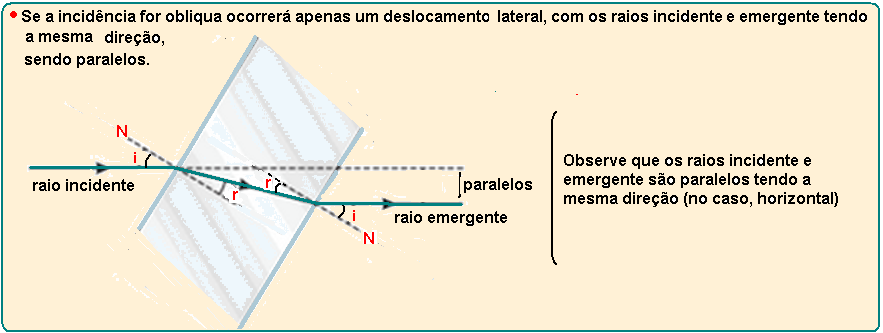
Sempre que um feixe de luz monocromática (uma só cor, no caso, verde) incide sobre uma lâmina de faces paralelas (placa plana do exercício) imersa em um mesmo meio, o raio incidente e o raio emergente são paralelos não sofrendo mudança na direção, no caso horizontal, veja a análise nas figuras abaixo:

R- A

 

Confira os exercícios com resolução comentada