Reflexão e Refração de Ondas
Reflexão e Refração de Ondas
Reflexão de uma onda
Uma onda sofre reflexão quando, propagando-se em um dado meio, atinge a interface de separação com outro meio e, em seguida, volta a se propagar no meio inicial.
Reflexão em meios unidimensionais
A reflexão de uma onda num meio unidimensional, como por exemplo, numa corda, pode ocorrer em duas situações:
![]() Extremidade fixa
Extremidade fixa ![]() A fonte (A) provoca uma oscilação completa e a onda se propaga com velocidade V até o ponto B que está fixo, preso, por exemplo, a uma parede.
A fonte (A) provoca uma oscilação completa e a onda se propaga com velocidade V até o ponto B que está fixo, preso, por exemplo, a uma parede.

Quando o pulso chega à B (extremidade fixa), cada ponto da corda aplica na parede uma força e, pelo princípio da ação e reação, a parede reagirá sobre cada ponto da corda com uma força de mesma intensidade, mesma direção mas sentido contrário, produzindo um pulso invertido após a reflexão, mas com a mesma velocidade V, pois o meio (corda) é o mesmo.
A amplitude A também será a mesma, supondo não haver perda de energia.
![]()
![]() Extremidade livre
Extremidade livre ![]() Neste caso, quando o pulso chega em B, cada ponto da corda não trocará forças com a parede, pois a argola de massa desprezível e sem atrito, sobe e desce, provocando, após a reflexão, um pulso que retornará sem inversão de fase, ou seja, idêntico ao
Neste caso, quando o pulso chega em B, cada ponto da corda não trocará forças com a parede, pois a argola de massa desprezível e sem atrito, sobe e desce, provocando, após a reflexão, um pulso que retornará sem inversão de fase, ou seja, idêntico ao

que chega, mas com a mesma velocidade V, pois o meio (corda) é o mesmo.
![]()
Reflexão em meios bidimensionais
A reflexão de uma onda num meio bidimensional, como por exemplo, na superfície da água de uma cuba, pode ocorrer em duas situações:
![]() Ondas circulares (esféricas)
Ondas circulares (esféricas) ![]() Quando a ponta de uma régua bate continua e periodicamente na superfície da água origina perturbações circulares (ondas circulares) que se movem na superfície da água, afastando-se do ponto onde as perturbações são geradas.
Quando a ponta de uma régua bate continua e periodicamente na superfície da água origina perturbações circulares (ondas circulares) que se movem na superfície da água, afastando-se do ponto onde as perturbações são geradas.

Como determinar o formato das ondas circulares refletidas num obstáculo
Considere as ondas circulares (esféricas) da figura 1, produzidas pela fonte F e que incidem no obstáculo plano P.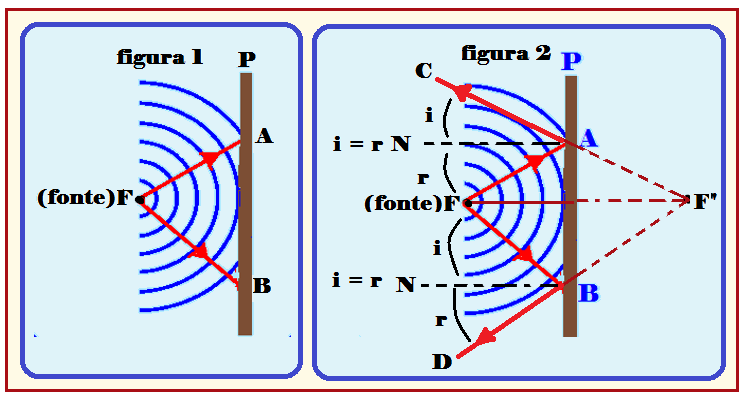
FA e FB são dois raios de onda incidentes, perpendiculares a cada frente de onda e que indicam a direção e sentido de sua propagação.
Ao atingirem o obstáculo P essas ondas sofrem reflexão de modo que cada ponto do obstáculo torna-se fonte de uma onda secundária.
Pelo princípio da reflexão os raios incidentes FA e FB sofrem reflexão e retornam (AC e BD), de modo que os ângulos i e r entre a normal N, e os raios incidente e refletido sejam iguais, ou seja, i = r (figura 2).
Então, todos os raios refletidos se encontram em um ponto comum F’, e as ondas refletidas se comportam como se fossem originadas por uma fonte F’, simétrica de F, em relação ao obstáculo refletor P.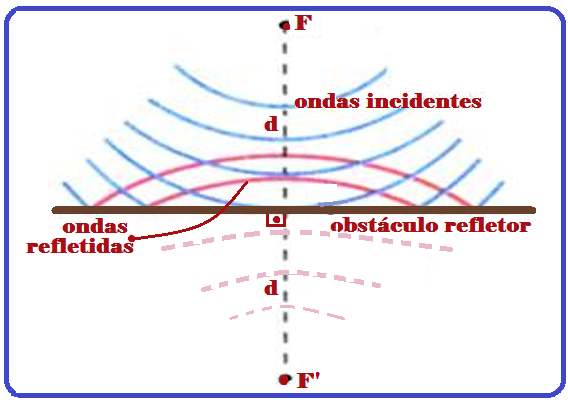
Assim, para você esquematizar as ondas refletidas, basta você localizar a fonte F’, simétrica a F e, a partir dela traçar as ondas refletidas, em vermelho na figura.
Lembre-se de que a velocidade de propagação e o comprimento de onda das ondas incidentes e refletidas são os mesmos, pois o meio é o mesmo.
A frequência também não muda, é a da fonte.
Ondas planas (retas) ![]() Podem ser produzidas tocando-se leve e continuamente a superfície da água com uma régua (fonte) na posição indicada na figura.
Podem ser produzidas tocando-se leve e continuamente a superfície da água com uma régua (fonte) na posição indicada na figura.
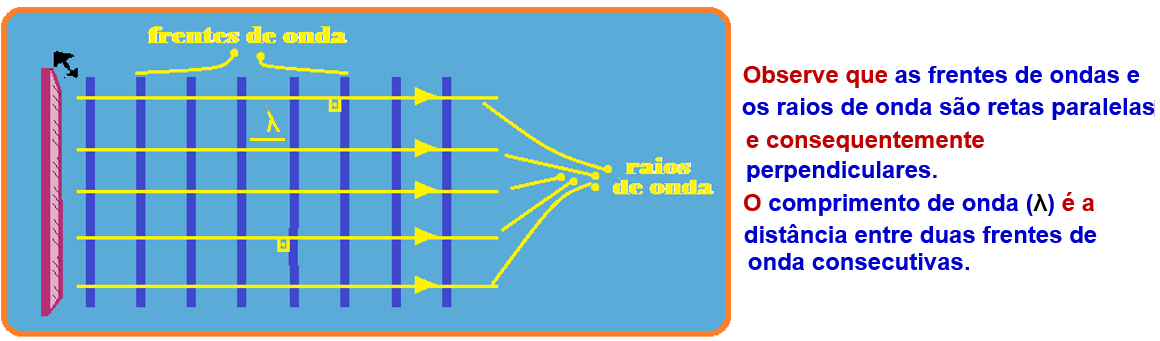
Como determinar o formato das ondas retas (planas) refletidas num obstáculo
Considere as ondas retas da figura 1, produzidas pela fonte F e que incidem no obstáculo plano P.
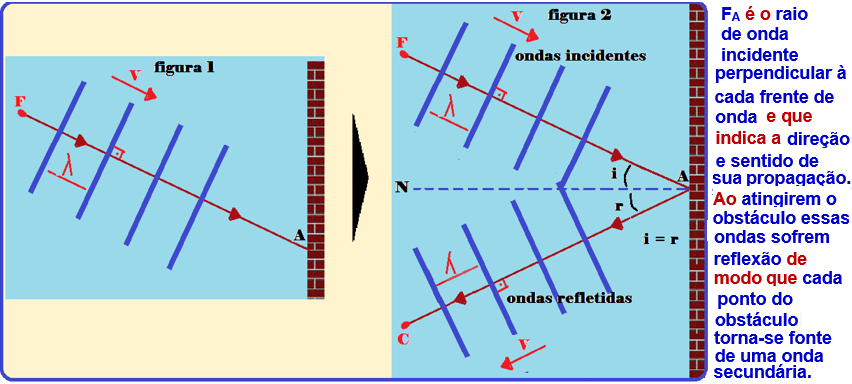
Pelo princípio da reflexão o raio incidente FA sofre reflexão e retorna (AC), de modo que os ângulos i e r entre a normal N, e o raio incidente e refletido sejam iguais, ou seja, i = r (figura 2)
Lembre-se de que a velocidade de propagação e o comprimento de onda das ondas incidentes e refletidas são os mesmos, pois o meio é o mesmo.
A frequência também não muda, é a da fonte.
O que você deve saber, informações e dicas
![]()
Conhecer o comportamento da reflexão de ondas em meios unidimensionais numa corda com extremidades fixas e livres.
![]()
Você deve saber como determinar formato das ondas retas (planas) e circulares (esféricas) refletidas num obstáculo, conforme explicado na teoria.
![]()
Não importa se o meio é uni, bi ou tridimensional, na reflexão das ondas, as ondas incidentes e refletidas tem sempre a mesma velocidade de propagação V (o meio é o mesmo), a mesma freqüência f (a fonte é a mesma) e consequentemente o mesmo comprimento de ondaλ, pois V = λ.f.
![]()
A amplitude A da onda não está relacionada com V, f e λ e sim com a energia transportada pela onda.
Quanto maior a energia, maior a amplitude e vice-versa.
Exemplos de reflexão de ondas planas:
Nas figuras I, II, III e IV, estão representas as frentes de ondas retas (planas) que incidem em anteparos. Os sentidos de propagação estão representados pelas setas.
Esboce, em cada caso, as frentes de onda após a reflexão.
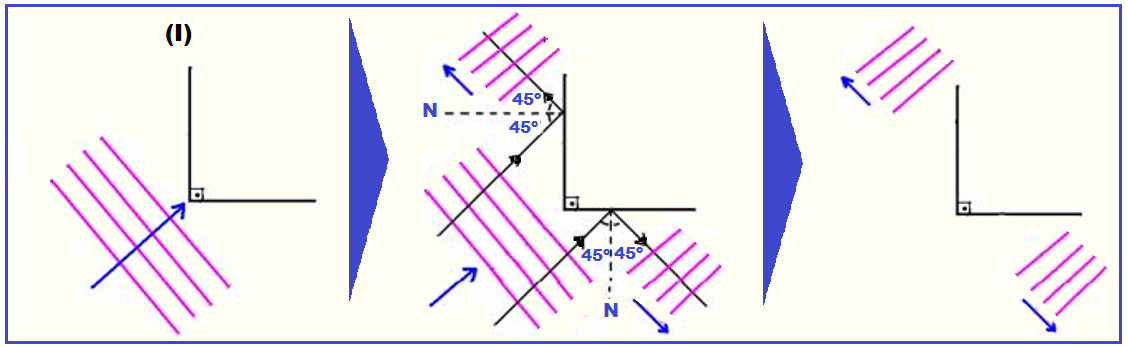
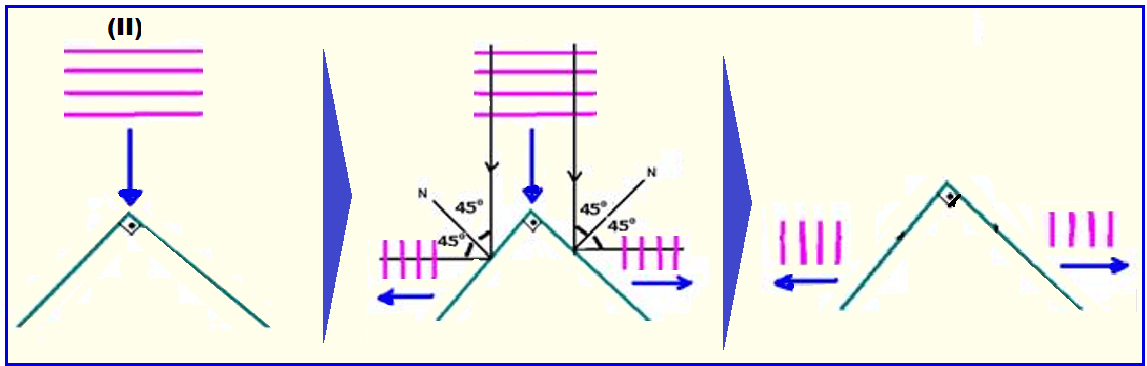
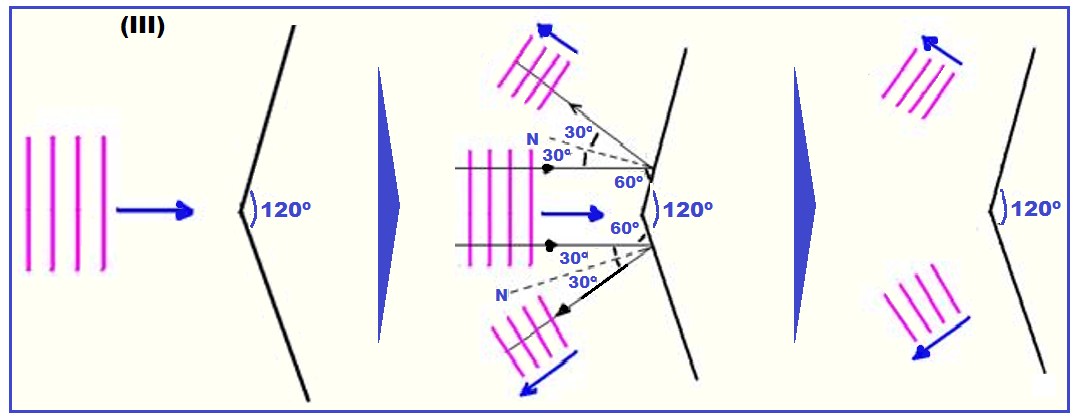
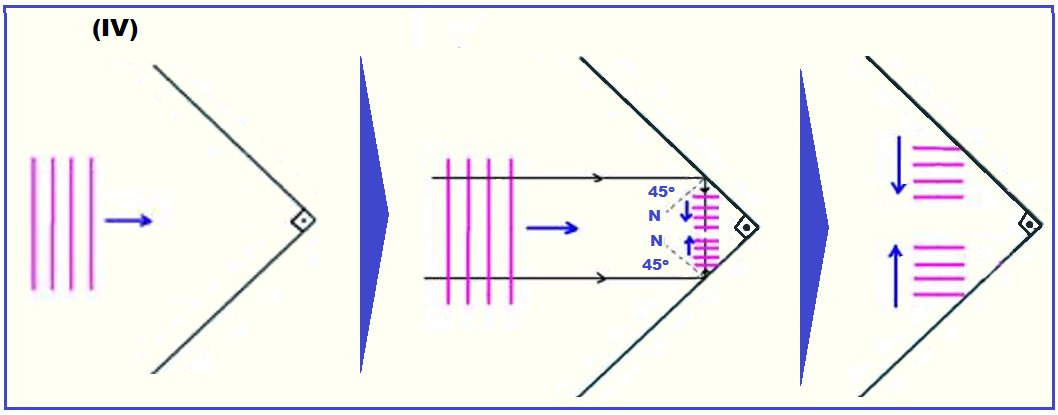
Lembre-se de que as ondas refletidas tem sempre a mesma velocidade de propagação, a mesma freqüência (da fonte) e o mesmo comprimento de onda.
Refração de ondas em meios unidimencionais
Refração de uma onda
A Refração de uma onda é um fenômeno que ocorre quando uma onda, muda seu meio inicial de propagação para outro meio de características diferentes, variando sua direção de propagação.
Considere duas cordas de diferentes densidades lineares de massa (µ = m/L), unidas, e o sistema preso numa parede com uma das extremidades fixas.
Vamos considerar três casos:
![]() 1o caso
1o caso ![]() A densidade linear (µ) das cordas é a mesma, ou seja, µ1 = µ2.
A densidade linear (µ) das cordas é a mesma, ou seja, µ1 = µ2.
Quando o pulso passa de uma corda para a outra, toda energia é transmitida, não ocorrerá reflexão e a onda continua como se estivesse no mesmo meio, mantendo todas suas

características (freqüência, amplitude, velocidade e comprimento de onda).
![]() 2o caso
2o caso ![]() A densidade linear da primeira corda (µ1) é maior do que a da segunda (µ2), ou seja, µ1 > µ2.
A densidade linear da primeira corda (µ1) é maior do que a da segunda (µ2), ou seja, µ1 > µ2.
Quando o pulso chega ao ponto de junção das cordas, ocorre ao mesmo tempo refração e reflexão. Esse ponto (junção) funciona como uma extremidade livre e o pulso refletido retorna sem inversão de fase.
O pulso refratado tem sempre a mesma fase do incidente.
Parte da energia do pulso incidente é transmitida ao pulso refratado e parte ao pulso refletido, diminuindo assim a amplitude desses dois pulsos, ou seja, A > A1 e A > A2.

A força de tração (T) nas duas cordas é a mesma e a velocidade em cada corda é fornecida por
![]()
Observe na expressão acima que a velocidade V é inversamente proporcional à densidade linear µ, assim, a velocidade da onda na corda mais densa “mais pesada” é menor do que a velocidade na corda menos densa “mais leve”. Então, V2 > V1.
A freqüência f é a mesma nas duas cordas, pois a fonte é a mesma.
V = λf ![]() f = V/λ
f = V/λ ![]() f = V1/λ1 e f = V2/λ2
f = V1/λ1 e f = V2/λ2 ![]() V1/λ1= V2/λ2 (I)
V1/λ1= V2/λ2 (I)
Observe na expressão (I) que, quanto maior a velocidade V maior o comprimento de onda λ. Portanto o comprimento de onda da corda menos densa é maior que o da corda mais densa.
![]() 3o caso
3o caso ![]() A densidade linear da primeira corda (µ1) é menor do que a da segunda (µ2), ou seja, µ1 < µ2.
A densidade linear da primeira corda (µ1) é menor do que a da segunda (µ2), ou seja, µ1 < µ2.
Quando o pulso chega ao ponto de junção das cordas, ocorre ao mesmo tempo refração e reflexão. Esse ponto (junção) funciona como uma extremidade fixa e o pulso refletido retorna com inversão de fase.
O pulso refratado tem sempre a mesma fase do incidente.
Parte da energia do pulso incidente é transmitida ao pulso refratado e parte ao pulso refletido, diminuindo assim a amplitude desses dois pulsos, ou seja, A > A1 e A > A2.

A freqüência (f) desses dois pulsos é a mesma, pois a fonte é a mesma. V1 > V2 e λ1 > λ2.
Refração de ondas em meios bidimensionais
Na refração a freqüência das ondas incidentes é a mesma que das ondas refratadas (a fonte é a mesma) e, como V = λf ![]() f = V/λ
f = V/λ ![]() V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
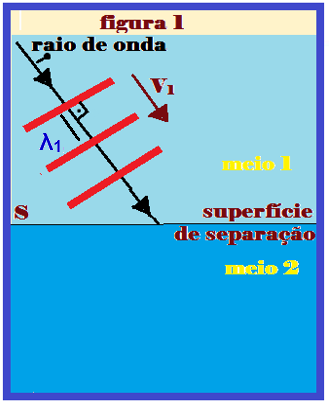
Considere dois meios diferentes 1 e 2 e ondas retas (planas) se propagando no meio 1, com velocidade V1 e comprimento de onda λ1, que vão incidir no meio 2, com velocidade V2 e comprimento de onda λ2 e, com V1 > V2. (figura I).
Sendo a velocidade da onda do meio 1 maior que a velocidade da onda no meio 2, o raio de onda, ao penetrar no meio 2 se aproximará da normal, com i > r e com λ1 > λ2.
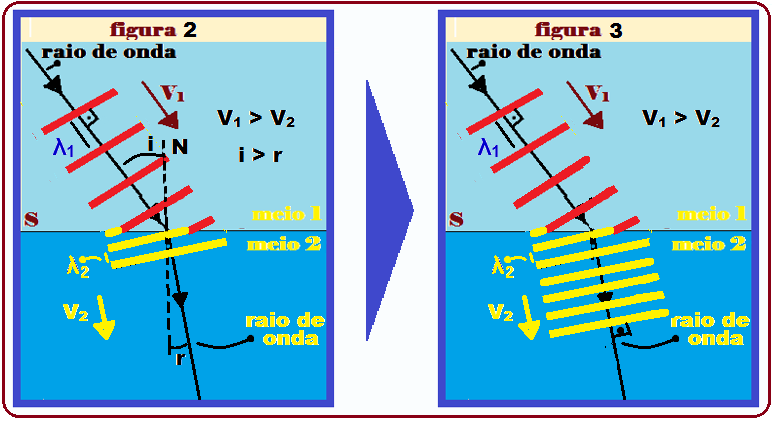
As figuras II e III mostram as etapas da refração.
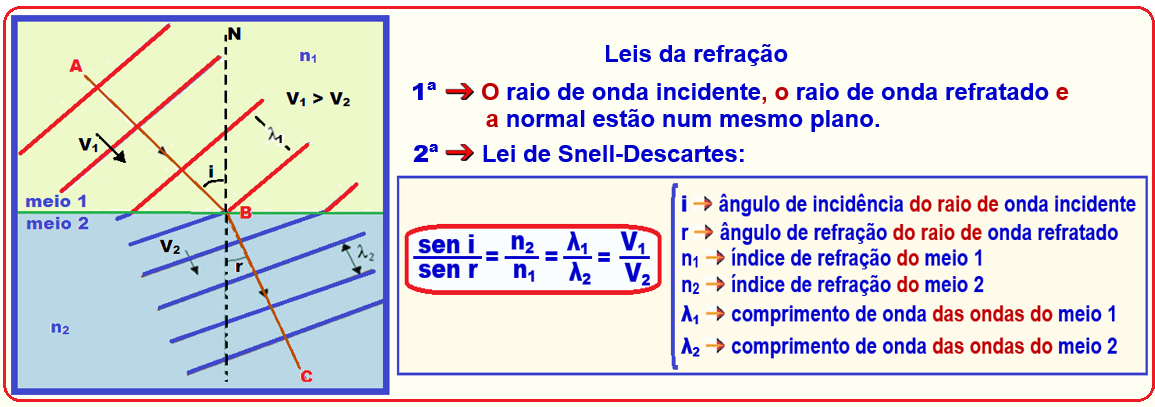
Informações e fórmulas necessárias para a resolução de exercícios sobre refração de ondas planas
Na figura abaixo, AB representa o raio de onda incidente, CD o raio de onda refratado, i o ângulo de incidência e r o ângulo de refração, bem como as relações matemáticas entre os elementos que envolvem o fenômeno da refração de ondas planas.

Na refração a freqüência das ondas incidentes é a mesma que das ondas refratadas (a fonte é a mesma) e, como V = λf ![]() f = V/λ
f = V/λ ![]() V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
Baseado nas expressões acima você pode concluir que:

Observação:
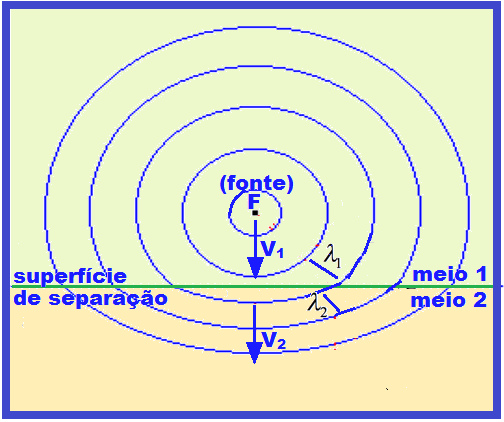
Dentro de certos limites as expressões acima também são válidas para refraação de ondas circulares (esféricas)
O que você deve saber, informações e dicas
![]()
Conhecer o comportamento da refração de ondas em meios unidimensionais numa corda, nos três casos, quando passa se deslocar em meios de diferentes densidades lineares de massa.
![]()
Você deve saber como determinar formato das ondas retas (planas) e circulares (esféricas), refratadas numa determinada superfície de separação, conforme explicado na teoria.
![]()
Informações e fórmulas necessárias para a resolução de exercícios sobre refração de ondas planas


Na refração a freqüência das ondas incidentes é a mesma que das ondas refratadas (a fonte é a mesma) e, como V = λf ![]() f = V/λ
f = V/λ ![]() V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
V e λ são diretamente proporcionais (maior V, maior λ e vice versa).
Baseado na lei de Snell-Descartes n1.seni = n2.senr = constante para o mesmo sistema de meios, você conclui que n.senα = constante e que o índice de refração n de um meio é inversamente proporcional ao seno do ângulo que o raio forma com esse meio.
Consequentemente n é inversamente proporcional a α, portanto maior n, menor α.
Baseado nas expressões acima você pode concluir que:

Observação:

Dentro de certos limites as expressões acima também são válidas para refração de ondas circulares (esféricas)
![]()
Para esboçar as ondas planas refratadas num dado exercício, você deve seguir as etapas, apresentas no exemplo a seguir:
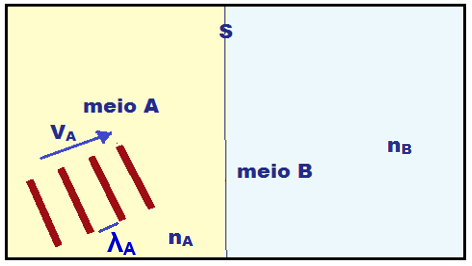
Na figura ao lado, esquematizar as ondas planas refratadas no meio B, a partir das ondas esquematizadas no meio A.
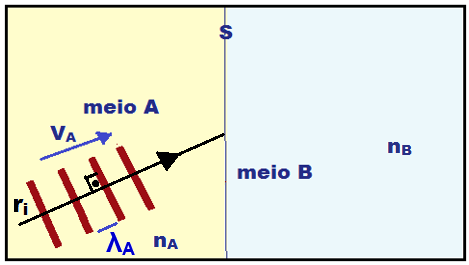
1a etapa ![]() Traçar o raio de onda incidente (ri) que é sempre perpendicular às frentes de onda.
Traçar o raio de onda incidente (ri) que é sempre perpendicular às frentes de onda.
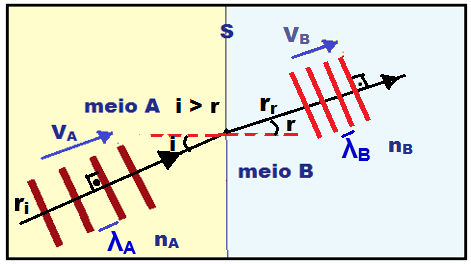
2a etapa ![]() Traçar o raio de onda refratado (rr), o ângulo de incidência (i), a normal (N) e o ângulo de refração (r). Supondo nA < nB, teremos que λA > λB, VA > VB e r < i (veja informações na teoria).
Traçar o raio de onda refratado (rr), o ângulo de incidência (i), a normal (N) e o ângulo de refração (r). Supondo nA < nB, teremos que λA > λB, VA > VB e r < i (veja informações na teoria).
3a etapa ![]() Utilizar a equação fundamental da ondulatória V = λ.f.
Utilizar a equação fundamental da ondulatória V = λ.f.
![]()
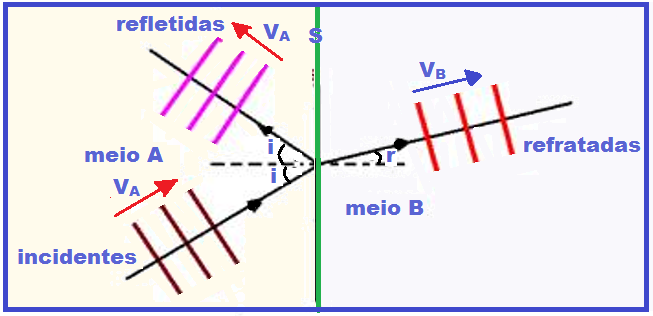
Se houver refração, sempre ocorrerá também reflexão.
![]()
As expressões:

são válidas também para ondas eletromagnéticas, como por exemplo, a luz.

![]()
A freqüência é característica da fonte e independe do meio. Assim, por exemplo, se uma fonte luminosa emitir um feixe de luz azul (freqüência 7.1014 Hz), em qualquer meio que este feixe luminoso estiver se propagando ele sempre será azul, pois terá sempre essa frequência.
O mesmo é válido para ondas.
![]()
Alguns exercícios interessantes resolvidos para que você possa se aprofundar no assunto:
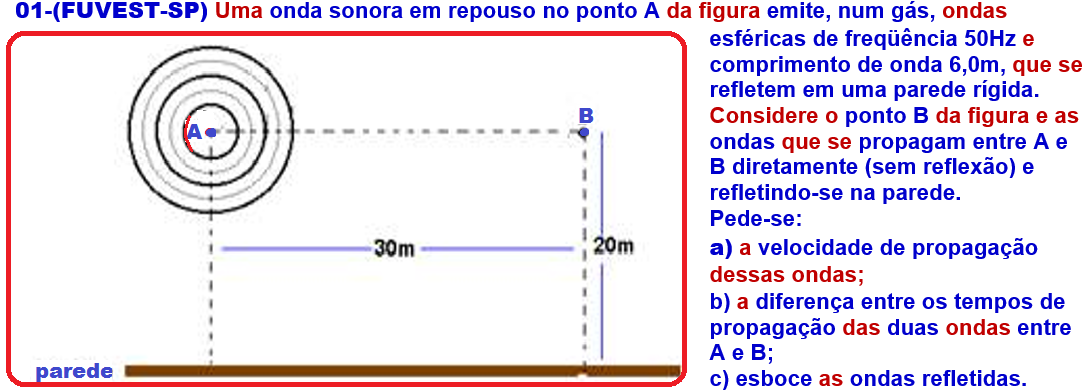
Resolução:
a) V = λ.f ![]() V = 6.50
V = 6.50 ![]() V = 300m/s.
V = 300m/s.
b) intervalo de tempo (Δt1) que a onda demora para ir de A até B ![]() V = ΔS/Δt1
V = ΔS/Δt1 ![]() 300 = 30/Δt1
300 = 30/Δt1
![]() Δt1 =1/10s
Δt1 =1/10s
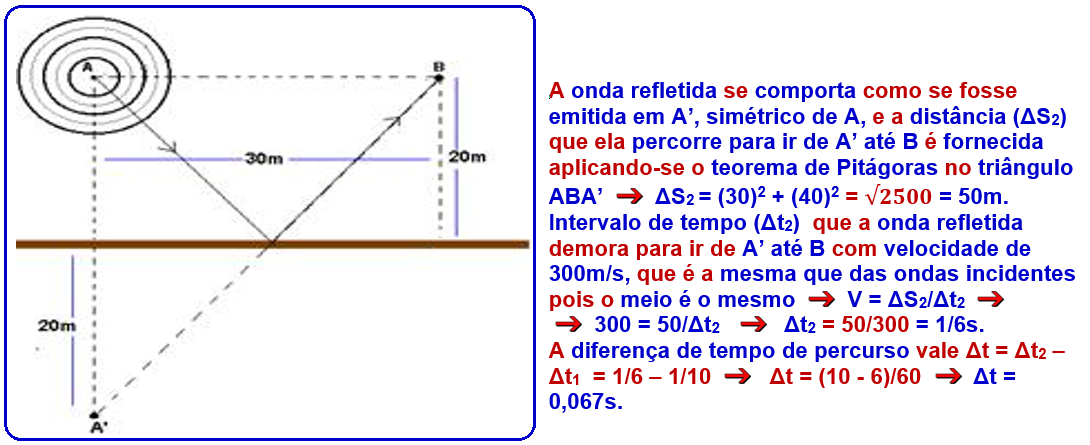
c)

02-(PUCC-SP) Na superfície da água parada de um tanque quadrado de 30cm de lado, provoca-se
no centro do mesmo uma onda que se propaga com frentes de onda circulares, com freqüência de 5Hz e velocidade de 8cm/s. 
a) Represente a configuração da frente de onda, depois de 2s de sua geração.
b) As ondas, ao se refletirem na parede do tanque retornam com, ou sem inversão de fase?
Justifique
Resolução:
a) Cálculo da distância percorrida pela onda em 2s ![]() V = ΔS/Δt
V = ΔS/Δt ![]() 8 = ΔS/2
8 = ΔS/2 ![]() ΔS = 16cm.
ΔS = 16cm.
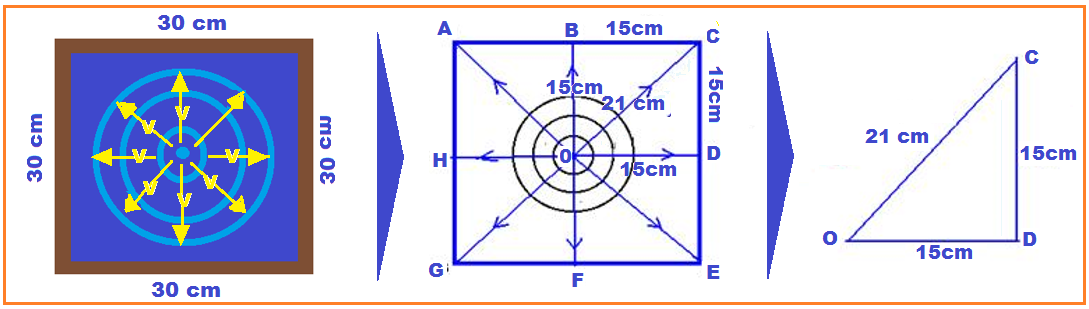
Aplicando o teorema de Pitágoras no triângulo OCD ![]() d2 = 152 + 152 = 2.152
d2 = 152 + 152 = 2.152 ![]() d = 15
d = 15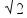 = 15.1,4
= 15.1,4
![]() d = 21 cm.
d = 21 cm.
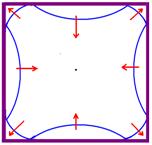
Observe nas figuras acima e na figura ao lado que, em t = 2s, a onda não chegou aos pontos A,C,E e G e que já está voltando dos pontos B, D, F e H.
b) Sem inversão de fase, pois as paredes comportam-se como extremidades livres.
03-(FUVEST-SP) Um canal de navegação de 4,0m de largura tem suas comportas semi-abertas, como está indicado na figura. Ondas planas propagam-se na superfície da água do canal com velocidade igual a 2,0m/s. Considere uma crista AB, na posição indicada na figura, no instante t=0.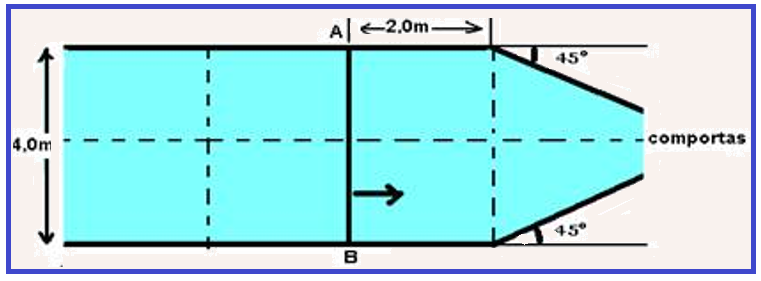
Esboce a configuração dessa crista depois de decorridos 1,5s, indicando a distância, em metros, entre seus extremos A’B’ nessa configuração (despreze efeitos da difração).
Resolução:
Vamos calcular a distância percorrida por cada ponto da onda no instante t = 1,5 s ![]() V = ΔS/Δt
V = ΔS/Δt
![]() 2 = ΔS/1,5
2 = ΔS/1,5 ![]() ΔS = 3,0m.
ΔS = 3,0m.
Verifique nas figuras abaixo que ![]() AA’ = BB’ = ΔS = 3,0m e que PP’ = QO’ = ΔS = 3,0m.
AA’ = BB’ = ΔS = 3,0m e que PP’ = QO’ = ΔS = 3,0m.
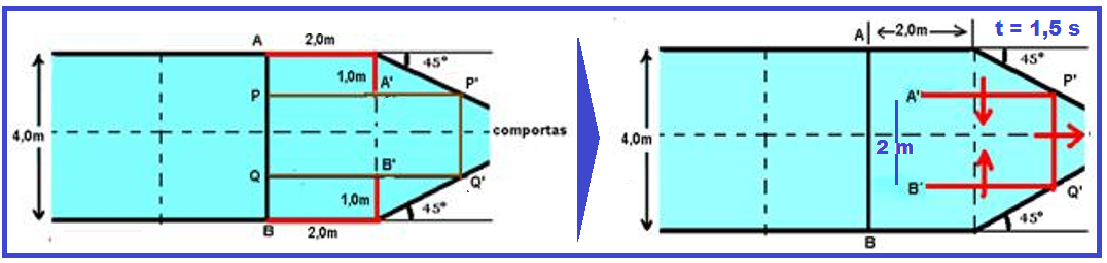
Quando t = 1,5s:
Os pontos da onda entre A’ e P’ já atingiram o anteparo e estão retornando. O mesmo acontece com os pontos da onda entre B’ e Q’.
Os pontos P’ e Q’ estão no anteparo.
Os pontos da onda entre P’ e Q’ ainda não atingiram o anteparo e estão se deslocando para a direita.
![]()
Se você deseja ainda mais se aprofundar no assunto confira as resoluções dos exercícios de números 03, 04, 06, 11, 17, 24, 32, 38 e 43.
