UEM- PR – 2020
Compare essa e outras resoluções da UEM- PR – 2020
e dos vestibulares das demais Universidades pelo fisicaevestibular.com.br com outras e você verá que ela:
Tem melhor visual e mais ilustrações esclarecedoras.
Foi feito para alunos que realmente tenham dificuldades nos conceitos de Física e Matemática procurando sempre explicar os menores detalhes.
Não coloca apenas as fórmulas procurando sempre mostrar suas procedências e utilidades.
Sempre que preciso procura explicar por meio de desenhos e ilustrações.
Não queima etapas explicando sequência por sequência.
A preocupação com que o aluno entenda as resoluções é muito grande. O professor se coloca no lugar do aluno.
Muitas vezes fornece informações além das necessárias para as resoluções, mas úteis nos próximos vestibulares.
![]() E
muito, muito mais.
E
muito, muito mais.

A Universidade Estadual de Maringá (UEM) é uma instituição pública de ensino superior, mantida pelo Estado do Paraná. Com sede na cidade de Maringá, possui campus nas cidades de Cianorte, Cidade Gaúcha, Goioerê, Ivaiporã e Umuarama, e extensões nos distritos de Floriano (Maringá) (Centro de Psicultura) e Iguatemi (Maringá) (Fazenda Experimental) e na cidade de Porto Rico(Centro de Pesquisa em Porto Rico – Nupélia). A instituição oferta 63 cursos de Graduação, 85 cursos de Especialização, 30 cursos de Mestrado, 17 cursos de Doutorado e 2 cursos de Pós-Doutorado. Considerada uma das melhores universidades do Brasil, a UEM possui cursos de destaque em todo o âmbito nacional, os quais atraem estudantes do país inteiro. O Campus Sede, com aproximadamente 100 hectares, fica no centro de Maringá, e tem uma população universitária de aproximadamente 20 mil pessoas, entre alunos, professores e servidores.
Em 2012, a Universidade Estadual de Maringá foi classificada como a melhor universidade do estado do Paraná, pelo quarto ano consecutivo, segundo o Índice Geral de Cursos (IGC) do Ministério da Educação.
A UEM realiza anualmente os Vestibulares de Inverno, com provas em julho, e de Verão com provas em dezembro. Também abre vestibulares para os cursos a distância, de acordo com sua implantação.

01- Universidade Estadual de Maringá (UEM) – PR - 2020

Uma
espira
quadrada, de lado igual a
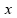 (em m),
tem resistência
elétrica total igual a
(em m),
tem resistência
elétrica total igual a
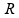 (em
Ω). Essa espira está submetida a um campo
magnético espacialmente uniforme e variável no tempo,
de módulo
igual a
(em
Ω). Essa espira está submetida a um campo
magnético espacialmente uniforme e variável no tempo,
de módulo
igual a
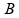 (em
T), cujas linhas de indução são perpendiculares
ao plano da espira.
Durante um período de tempo igual a
(em
T), cujas linhas de indução são perpendiculares
ao plano da espira.
Durante um período de tempo igual a
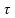 (em s), o módulo do campo cresce ou decresce linearmente com o tempo
de tal modo que
(em s), o módulo do campo cresce ou decresce linearmente com o tempo
de tal modo que
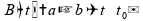 ,
no intervalo
,
no intervalo
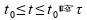 em que a e b são constantes, e
em que a e b são constantes, e
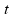 é dado em s. Nessa situação, o módulo da corrente
elétrica induzida na espira é igual a
é dado em s. Nessa situação, o módulo da corrente
elétrica induzida na espira é igual a
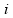 (em A). Sobre
a corrente elétrica induzida na espira durante o período de tempo,
(em A). Sobre
a corrente elétrica induzida na espira durante o período de tempo,
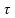 assinale o que for correto.
assinale o que for correto.
01)
Se
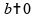
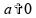 ,
,
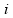 será igual a uma constante não nula.
será igual a uma constante não nula.
02)
Se
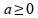 e
e
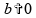 ,
,
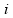 é constante durante o período
é constante durante o período
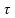 .
.
04)
Se
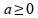 e
e
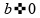 ,
,
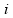 pode ser igual a zero dependendo dos valores numéricos de
pode ser igual a zero dependendo dos valores numéricos de
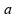 e
e
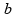
08)
Se aumentarmos a resistência elétrica da espira para
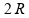 mantendo o comprimento de cada lado da espira igual a
mantendo o comprimento de cada lado da espira igual a
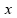 ,
o módulo da corrente elétrica induzida será
,
o módulo da corrente elétrica induzida será
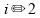 .
.
16)
Se aumentarmos o comprimento de cada lado da espira para
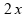 mantendo a resistência total da espira em
mantendo a resistência total da espira em
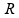 o módulo da corrente elétrica induzida será
o módulo da corrente elétrica induzida será
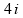 .
.
02- Universidade Estadual de Maringá (UEM) – PR - 2020

Um automóvel trafega por uma avenida, em um trecho retilíneo e horizontal, no sentido Norte-Sul. Em certo ponto do percurso, esse automóvel se encontra parado em um semáforo.

A
partir do instante em que o semáforo abre (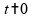 ),
o automóvel: a) permanece
parado por
),
o automóvel: a) permanece
parado por
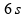 ;
b) passa
de
;
b) passa
de
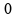 a
a
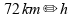 em
em
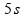 com aceleração constante;
e c) permanece
com velocidade constante nos próximos
com aceleração constante;
e c) permanece
com velocidade constante nos próximos
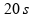 .
Sejam
.
Sejam
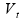 e
e
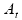 a velocidade escalar média e a aceleração escalar média do
automóvel, respectivamente,
calculadas
no intervalo de
a velocidade escalar média e a aceleração escalar média do
automóvel, respectivamente,
calculadas
no intervalo de
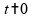 a t (em segundos).
Sobre o movimento desse automóvel durante
o período considerado
a t (em segundos).
Sobre o movimento desse automóvel durante
o período considerado
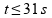 ,
assinale o que for correto.
,
assinale o que for correto.
01)
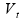 > 0 para qualquer
> 0 para qualquer
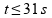 .
.
02)
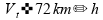 para qualquer
para qualquer
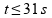 .
.
04)
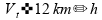 para
para
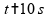 .
.
08)
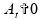 para qualquer
para qualquer
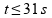 .
.
16)
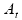 decresce com o aumento de t nos últimos
decresce com o aumento de t nos últimos
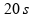 .
.
03- Universidade Estadual de Maringá (UEM) – PR - 2020

As posições (em metros) em função do tempo (em segundos) ocupadas por um móvel sobre uma

trajetória
retilínea
são representadas pela função horária
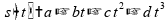 ,
sendo
,
sendo
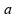 ,
,
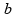 ,
,
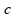 e
e
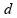 constantes. Assinale o que for correto.
constantes. Assinale o que for correto.
01)
Esse móvel se movimenta com velocidade constante se
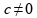 e
e
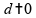 .
.
02)
Esse móvel se movimenta com aceleração constante se
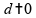 .
.
04)
A constante
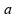 é adimensional.
é adimensional.
08)
A constante
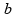 representa a velocidade do móvel no instante
representa a velocidade do móvel no instante
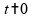 , para
, para
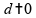 .
.
16)
A constante
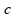 tem dimensão de aceleração.
tem dimensão de aceleração.
04- Universidade Estadual de Maringá (UEM) – PR - 2020

Considere fluidos incompressíveis, não viscosos e em regime estacionário. Assinale o que for

correto.
01) A velocidade de um fluido em um tubo de diâmetro variável é menor na região de menor área de seção transversal.
02) A pressão de um fluido em um tubo horizontal de diâmetro variável é maior na região de maior velocidade.
04) A pressão de um fluido em movimento em um tubo de diâmetro constante é menor na região de maior altura.
08) A movimentação ascendente ou descendente de submarinos submersos no mar pode ser explicada pela equação de Bernoulli.
16) A elevação de um automóvel sobre um dos pistões de uma prensa hidráulica pode ser explicada pelo princípio de Pascal.
05- Universidade Estadual de Maringá (UEM) – PR - 2020

Durante um sarau na casa da senhora de Bargeton, a senhora du Brossard refere-se à sua própria filha para o senhor de Séverac da seguinte forma: “Camille tem tanta inteligência que entenderá imediatamente tudo o que o senhor lhe disser.

Não compreendeu ela um dia a razão inversa do quadrado das distâncias?” (BALZAC, H. de. Ilusões perdidas. V. 1. São Paulo: Abril, 2010, p. 104). Em qual(is) força(s) indicada(s) a seguir a razão inversa do quadrado das distâncias está presente?
01) Na força gravitacional entre duas partículas.
02) Na força elástica sobre uma partícula.
04) Na força eletrostática entre duas partículas eletrizadas.
08) Na força de resistência do ar sobre uma esfera maciça.
16) Na força magnética sobre uma partícula eletrizada em um campo magnético uniforme.
06- Universidade Estadual de Maringá (UEM) – PR - 2020

Um
cubo de gelo de
massa igual a
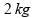 ,
à temperatura
inicial de
,
à temperatura
inicial de
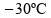 ,
é colocado em um forno de temperatura controlada e absorve
calor à razão constante de 2000 cal/min.
,
é colocado em um forno de temperatura controlada e absorve
calor à razão constante de 2000 cal/min.

Sejam
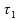 ,
,
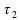 e
e
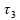 períodos de tempo que se referem, respectivamente, ao 1)
tempo de aquecimento do gelo (antes da fusão);
2) tempo de fusão do gelo a 0º C;
e 3)
tempo de aquecimento da água (após a fusão) até que sua
temperatura alcance 30 ºC.
Considere que o
calor específico do gelo, o calor específico da água e o calor
específico latente de fusão do gelo sejam, respectivamente, iguais
a 0,50 cal/(g ºC), 1,00cal/(g º C) e 80,00 cal/g. Nessas
condições, assinale o que for correto.
períodos de tempo que se referem, respectivamente, ao 1)
tempo de aquecimento do gelo (antes da fusão);
2) tempo de fusão do gelo a 0º C;
e 3)
tempo de aquecimento da água (após a fusão) até que sua
temperatura alcance 30 ºC.
Considere que o
calor específico do gelo, o calor específico da água e o calor
específico latente de fusão do gelo sejam, respectivamente, iguais
a 0,50 cal/(g ºC), 1,00cal/(g º C) e 80,00 cal/g. Nessas
condições, assinale o que for correto.
01)
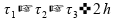
02)
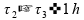
04)
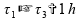
08)
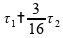
16)
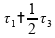
07- Universidade Estadual de Maringá (UEM) – PR - 2020

Em relação às radiações térmicas, assinale o que for correto.

01) Todo corpo emite energia na forma de radiações térmicas se sua temperatura (medida na escala Kelvin) não for nula.
02) Quando a superfície de um corpo está na temperatura ambiente, a radiação térmica emitida por ele é predominantemente infravermelha.
04) A quantidade total de energia emitida por unidade de tempo e por unidade de área da superfície externa de um corpo a uma temperatura (medida na escala Kelvin) é diretamente proporcional ao quadrado dessa temperatura.
08) Se a temperatura de um corpo permanece constante ao longo do tempo, então ele não emite nem absorve energia na forma de radiação térmica.
16) Em uma mesma temperatura, as radiações emitidas por qualquer corpo negro são independentes do material de que ele é feito.
08- Universidade Estadual de Maringá (UEM) – PR - 2020

Um
objeto
puntiforme
está localizado sobre
o eixo principal de um espelho esférico côncavo (espelho de Gauss),
a uma distância
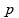 do vértice
do vértice
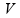 do espelho.
do espelho.

Nessas condições, a
imagem real
do objeto também está
localizada sobre o eixo, a uma distância
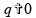 do vértice (com
do vértice (com
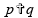 ).
Considere que
).
Considere que
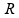 é o raio de curvatura
do espelho e que
é o raio de curvatura
do espelho e que
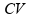 é o segmento de reta delimitado pelo centro de curvatura C e pelo
vértice. V Sobre
esse sistema, assinale
o que for correto.
é o segmento de reta delimitado pelo centro de curvatura C e pelo
vértice. V Sobre
esse sistema, assinale
o que for correto.
01)
A distância focal do espelho é igual a
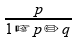
02)
Se o raio de curvatura do espelho for numericamente igual a ,
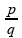 a distância do objeto ao vértice será numericamente igual a
a distância do objeto ao vértice será numericamente igual a
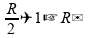 .
.
04)
Se a distância entre o objeto e sua imagem for igual a
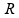 então a distância do objeto ao vértice será igual a
então a distância do objeto ao vértice será igual a
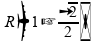 .
.
08)
O foco principal situa-se no ponto médio do segmento
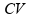
16)
Os focos secundários do espelho estão localizados sobre seu eixo
principal, na região delimitada pelo segmento
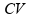 .
.
Resolução comentada das questões de Física da UEM – PR - 2020
01-
A lei de Lenz está resumida no quadro abaixo.

Vamos calcular o fluxo magnético para o sistema descrito no enunciado.
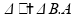
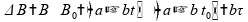
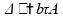
A diferença de potencial então torna-se:
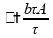
Utilizando
a
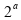 Lei de Ohm:
Lei de Ohm:
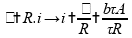
Obtemos então a expressão da corrente para o circuito. Vamos, portanto, avaliar cada uma das afirmações.
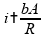
Se
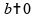
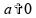 ,
,
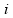 será igual a uma constante não nula.
será igual a uma constante não nula.
Se
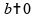 ,
,
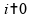 ,
logo esta alternativa
está errada.
,
logo esta alternativa
está errada.
Se
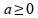 e
e
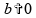 ,
,
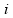 é constante durante
o período
é constante durante
o período
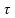 .
.
De
fato, pela fórmula demonstrada, essa
alternativa é verdadeira,
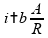
Se
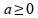 e
e
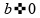 ,
,
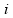 pode ser igual
a zero dependendo dos valores numéricos de
pode ser igual
a zero dependendo dos valores numéricos de
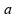 e
e
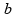
Falso,
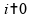 apenas se
apenas se
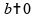 ou
ou
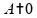 .
.
Se
aumentarmos a resistência elétrica da espira para
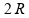 mantendo o comprimento de cada lado da espira igual a
mantendo o comprimento de cada lado da espira igual a
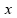 ,
o módulo da corrente elétrica induzida será
,
o módulo da corrente elétrica induzida será
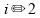 .
.
Verdadeiro,
se
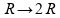 ,
temos que a corrente se modifica para
,
temos que a corrente se modifica para
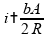 ,
que
é a metade
da corrente original.
,
que
é a metade
da corrente original.
Se
aumentarmos o comprimento de cada lado da espira para
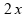 mantendo a resistência total da espira em
mantendo a resistência total da espira em
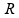 o módulo da corrente elétrica induzida será
o módulo da corrente elétrica induzida será
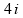 .
.
Verdadeiro,
pois
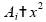 ,
logo
,
logo
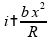 ,
se
modificarmos a espira, a área se torna
,
se
modificarmos a espira, a área se torna
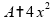 ,
e
a corrente passa a ser
,
e
a corrente passa a ser
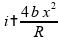 ,
que
é quatro
vezes maior que a corrente original.
,
que
é quatro
vezes maior que a corrente original.
Portanto, as alternativas corretas são 02), 08) e 16).
02-
Velocidade escalar média e aceleração escalar média são calculados com as expressões, respectivamente, posicionadas logo abaixo.


Para encontrar a velocidade escalar média e a aceleração média no intervalo de tempo de t, precisamos saber as funções horárias do Movimento Retilíneo Uniforme (com aceleração nula):

E do Movimento Retilíneo Uniformemente Variado (aceleração diferente de zero), em conjunto com a expressão da velocidade em função do tempo:


Vamos avaliar cada uma das afirmações:
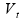 > 0 para qualquer
> 0 para qualquer
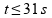 .
.
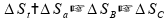
Em
que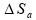 ,
,
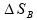 e
e
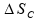 são, respectivamente, as variações espaciais ocorridas nos
instantes (a), (b) e (c) descritos no enunciado.
são, respectivamente, as variações espaciais ocorridas nos
instantes (a), (b) e (c) descritos no enunciado.
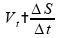
Para
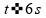 ,
o carro está parado, então
,
o carro está parado, então
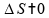 ,
logo, neste intervalo,
,
logo, neste intervalo,
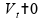 .
Portanto, esta afirmativa
não é válida para
todos os valores de
.
Portanto, esta afirmativa
não é válida para
todos os valores de
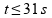 .
.
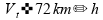 para qualquer
para qualquer
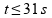 .
.
Por
avaliarmos
todo o intervalo para
calcular
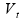 ,
a expressão se torna:
,
a expressão se torna:
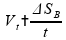
E
mesmo que no intervalo (b) a velocidade atinja
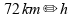 ,
a
velocidade escalar média de todo o percurso nunca supera este valor,
por este veículo ter ficado parado inicialmente
,
a
velocidade escalar média de todo o percurso nunca supera este valor,
por este veículo ter ficado parado inicialmente
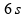 .
.
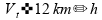 para
para
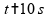 .
.
Para
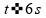 a velocidade
e a aceleração são nulas,
então
a velocidade
e a aceleração são nulas,
então
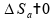 .
.
Para
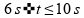 o movimento é retilíneo
uniformemente variado,
com velocidade
inicial
o movimento é retilíneo
uniformemente variado,
com velocidade
inicial
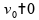 ,
portanto:
,
portanto:
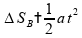
È
necessário então encontrar a aceleração a qual o carro está
sujeito neste intervalo de tempo. Para isso, utilizamos a informação
do enunciado de que o veículo
partiu do repouso e acelerou até ter a velocidade de
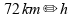 .
Para
converter esta velocidade para
.
Para
converter esta velocidade para
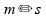 basta dividir o valor por
basta dividir o valor por
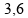 ,
e se quisermos converter de
,
e se quisermos converter de
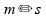 para
para
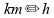 se deve multiplicar por
se deve multiplicar por
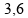 .
Logo, calculamos a aceleração utilizando a equação da velocidade:
.
Logo, calculamos a aceleração utilizando a equação da velocidade:
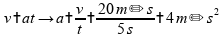
Substituimos
a aceleração obtida na equação de
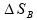 :
:
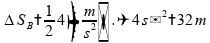
E,
enfim, podemos calcular a velocidade média, lembrando que o
intervalo
de tempo engloba os dois intervalos, tanto
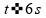 quanto
quanto
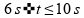 .
.
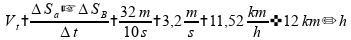
Portanto, esta alternativa também é verdadeira
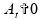 para qualquer
para qualquer
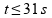 .
.
Esta
afirmativa não é válida, pois em
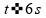 ,
o veículo está em repouso,
logo,
,
o veículo está em repouso,
logo,
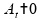 neste intervalo de tempo.
neste intervalo de tempo.
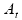 decresce com o aumento de
t nos
últimos
decresce com o aumento de
t nos
últimos
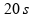 .
.
Como dito anteriormente, a aceleração escalar média é dada pela relação:
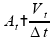
Para
avaliar a variação de
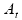 ,
vamos observar quando
,
vamos observar quando
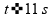 .
.
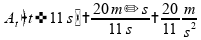
Após
este intervalo, o veículo não acelera mais,
mas o tempo
continua a contar.
Logo, a aceleração escalar média tende a diminuir, pois
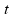 está no denominador e aumenta cada vez mais,
dimuindo
está no denominador e aumenta cada vez mais,
dimuindo
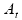 .
.
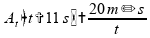
Portanto:
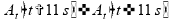
Logo, essa afirmação está correta.
Portanto, as alternativas 02), 04) e 16) estão corretas.
03-
Vamos avaliar cada uma das afirmações.
Esse
móvel se movimenta com velocidade constante se
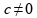 e
e
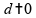 .
.
Com o auxílio do quadro abaixo podemos descartar algumas das propostas nas alternativas do exercício.

Ao observar a expressão:
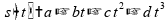
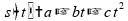
O
termo c
que acompanha o termo
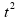 é
o dobro
de uma aceleração,
de acordo com a fórmula do quadro acima, logo o
móvel não se move com velocidade constante. Portanto esta afirmação
é falsa.
é
o dobro
de uma aceleração,
de acordo com a fórmula do quadro acima, logo o
móvel não se move com velocidade constante. Portanto esta afirmação
é falsa.
Esse
móvel se movimenta com aceleração constante se
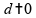 .
.
Analogamente ao ítem anterior, levando esta proposta ao pé da letra, temos:
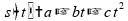
Em
que a aceleração
é dada por
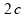 .
Portanto esta
alternativa está correta.
.
Portanto esta
alternativa está correta.
A
constante
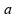 é adimensional.
é adimensional.
A aceleração é definida como:

Podemos
fazer a análise
dimensional da grandeza.
Sabendo que velocidade possui unidade de
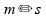 e que tempo possui unidade de
e que tempo possui unidade de
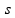 ,
a aceleração possui a unidade de:
,
a aceleração possui a unidade de:
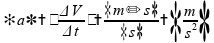
Logo, não é uma grandeza adimensional, invalidando esta afirmação.
A
constante
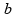 representa a velocidade do móvel no instante
representa a velocidade do móvel no instante
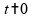 , para
, para
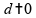 .
.
Esta alternativa está correta, pois em conjunto com a equação horária, temos também a equação da velocidade, dada por:

A
constante
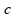 tem dimensão de aceleração.
tem dimensão de aceleração.
Se
nós supormos que
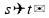 está em metros,
temos que:
está em metros,
temos que:
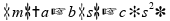
Para
satisfazer a igualdade, é necessário que
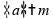 ,
,
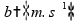 e
e
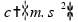 ,
sendo
,
sendo
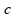 justamente com unidade de medida de aceleração, logo esta
alternativa está correta.
justamente com unidade de medida de aceleração, logo esta
alternativa está correta.
Portanto, as alternativas corretas são 02), 08) e 16).
04- Vamos avaliar cada uma das afirmativas com breves revisões dos conceitos envolvidos.
A velocidade de um fluido em um tubo de diâmetro variável é menor na região de menor área de seção transversal.

Logo,
se
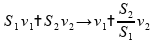 ,
então
se
,
então
se
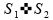 implica que
implica que
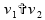 ,
logo
esta alternativa está incorreta.
,
logo
esta alternativa está incorreta.
A pressão de um fluido em um tubo horizontal de diâmetro variável é maior na região de maior velocidade.
Pela mesma argumentação do ítem anterior, esta alternativa está correta.
A pressão de um fluido em movimento em um tubo de diâmetro constante é menor na região de maior altura.

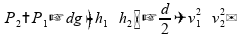
Como para um fluído ideal a velocidade é constante quando não há variação de diâmetro, esta equação se reduz a
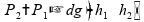
Se
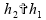 ,
então
,
então
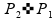 ,
logo esta alternativa está incorreta.
,
logo esta alternativa está incorreta.
A movimentação ascendente ou descendente de submarinos submersos no mar pode ser explicada pela equação de Bernoulli.
A
movimentação ascendente ou descendente de um submarino pode ser
explicada pelo princípio de Arquimedes, que é um caso especial da
equação de Bernoulli quando
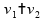 .
.
A elevação de um automóvel sobre um dos pistões de uma prensa hidráulica pode ser explicada pelo princípio de Pascal.
O princípio de Pascal enuncia que: “O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitido integralmente (ou seja, sem redução) a todos os pontos desse líquido e também às paredes do recipiente onde está contido”.
Para um elevador hidráulico, vale a situação descrita abaixo:

A
pressão comunicada do ponto 1 é transmitida ao ponto 2
integralmente quando temos um fluído ideal, da mesma maneira como é
enunciado o princípio de Pascal.
Portanto, esta alternativa é verdadeira.
As alternativas corretas são 02), 08) e 16).
05-
Vamos analisar cada uma das informações e relaciona-las com uma breve revisão de cada conceito físico.
Na força gravitacional entre duas partículas.

De fato, a expressão segue a razão inversa com o quadrado da distância.
Na força elástica sobre uma partícula.

De fato, a expressão não segue a razão inversa com o quadrado da distância.
Na força eletrostática entre duas partículas eletrizadas.

De fato, a expressão segue a razão inversa com o quadrado da distância.
Na força de resistência do ar sobre uma esfera maciça.

De fato, a expressão não segue a razão inversa com o quadrado da distância.
Na força magnética sobre uma partícula eletrizada em um campo magnético uniforme.

De fato, a expressão não segue a razão inversa com o quadrado da distância.
Portanto, as alternativas corretas são 01) e 04).
06-
A quantidade de calor para aquecer uma amostra é dada por:

A quantidade de calor para mudar uma amostra de estado é dada por:

Vamos calcular a quantidade de calor em cada uma das etapas. Repare que as constantes fornecidas no enunciado estão com unidades em gramas, então convém utilizar a massa da amostra em gramas.
Para
a primeira etapa, a
quantidade de 2 kg (2000 g) é aquecida de
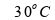 a
a
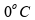 :
:
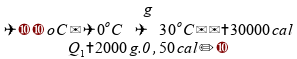
Para a segunda etapa, a quantidade de 2 kg (2000 g) passa do estado sólido para o líquido:
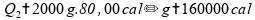
Para
a terceira e última etapa, a
quantidade de 2 kg (2000 g) é aquecida de
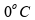 a
a
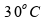 :
:
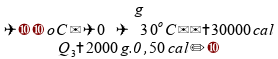
Podemos
calcular cada um dos tempos
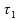 ,
,
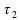 e
e
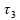 ,
sabendo que a energia fornecida ao sistema é de
,
sabendo que a energia fornecida ao sistema é de
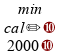 :
:
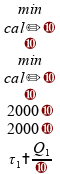
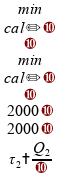
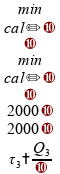
Vamos agora avaliar cada uma das alternativas.
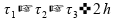
Se somarmos os intervalos de tempo, temos 2 horas:
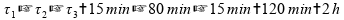
Invalidando esta alternativa.
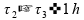
Se somarmos estes intervalos de tempo, temos mais de uma hora:
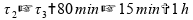
Invalidando esta alternativa.
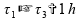
Se tomarmos estes intervalos de tempo, temos menos de uma hora:
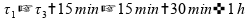
Invalidando esta alternativa.
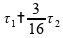
Se fizermos esta operação:
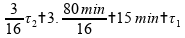
Logo, esta alternativa está correta.
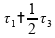
Como
sabemos
que
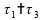 ,
esta alternativa é inválida.
,
esta alternativa é inválida.
Logo, somente a alternativa 16) está correta.
07-
Para este exercício, é necessário relembrar o conceito de radiação térmica. Pela Lei de Stefan-Boltzmann:

Vamos avaliar cada uma das alternativas:
Todo corpo emite energia na forma de radiações térmicas se sua temperatura (medida na escala Kelvin) não for nula.
De
fato, pela Lei de Stefan-Boltzmann, se
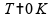 ,
,
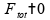 .
.
Quando a superfície de um corpo está na temperatura ambiente, a radiação térmica emitida por ele é predominantemente infravermelha.
De
fato, todo corpo emite energia desde que
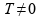 .
A radiação térmica está predominantemente na região do
infravermelho, logo esta é invisível ao olho humano,
mas ainda somos capazes de sentir esta radiação na pele em forma de
transferência de calor por radiação.
.
A radiação térmica está predominantemente na região do
infravermelho, logo esta é invisível ao olho humano,
mas ainda somos capazes de sentir esta radiação na pele em forma de
transferência de calor por radiação.
A quantidade total de energia emitida por unidade de tempo e por unidade de área da superfície externa de um corpo a uma temperatura (medida na escala Kelvin) é diretamente proporcional ao quadrado dessa temperatura.
Esta
alternativa é falsa. Esta
energia por unidade de tempo e por unidade de área é diretamente
proporcional a
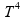 .
.
Se a temperatura de um corpo permanece constante ao longo do tempo, então ele não emite nem absorve energia na forma de radiação térmica.
Pela
Lei de Stefan-Boltzmann, se
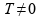 então há energia sendo emitida em forma de radiação térmica.
Além disso, a
absorção de energia também não cessa.
Logo, esta
alternativa está incorreta.
então há energia sendo emitida em forma de radiação térmica.
Além disso, a
absorção de energia também não cessa.
Logo, esta
alternativa está incorreta.
Em uma mesma temperatura, as radiações emitidas por qualquer corpo negro são independentes do material de que ele é feito.
Esta
alternativa é verdadeira. No caso de corpos negros (capazes de
absorver toda radiação incidente sobre eles),
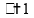 ,
e, portanto, o que diferencia as radiações é exclusivamente a
temperatura.
,
e, portanto, o que diferencia as radiações é exclusivamente a
temperatura.
Portanto, as alternativas corretas são 01), 02) e 16).
08- Para este exercício, vamos utilizar a equaçao de Gauss para espelhos esféricos.

Avaliando cada uma das alternativas.
A
distância focal do espelho é igual a
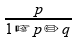
Partindo
da equação de Gauss para espelhos esféricos (com
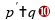 :
:
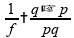
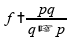
Colocando
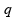 em
evidência,
obtemos:
em
evidência,
obtemos:
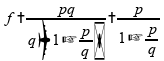
Portanto, esta alternativa é verdadeira.
Se
o raio de curvatura do espelho for numericamente igual a
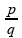 ,
a distância do objeto ao vértice será numericamente igual a
,
a distância do objeto ao vértice será numericamente igual a
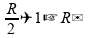 .
.
Novamente partindo da equação de Gauss para espelhos esféricos:
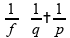
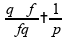
Substituindo
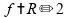 e
e
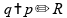 :
:
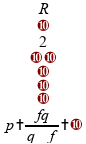
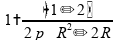
Obtemos então:
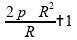
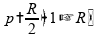
Portanto, a alternativa está correta.
Se
a distância entre o objeto e sua imagem for igual a
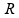 então a distância do objeto ao vértice será igual a
então a distância do objeto ao vértice será igual a
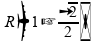 .
.
Partindo do mesmo ponto de um exercício anterior:
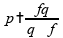
Mas agora utilizamos a distância entre objeto e imagem:
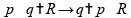
Para o numerador, temos:
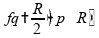
Para o denominador, temos:
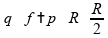
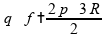
Substituindo na fração, obtemos:
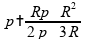
Que nos leva a uma equação do segundo grau:
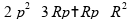
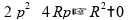
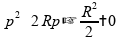
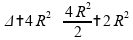
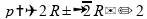
O
valor de
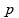 que faz sentido é o que está abaixo, por conta da imposição de
que
que faz sentido é o que está abaixo, por conta da imposição de
que
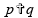 .
.
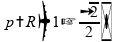
Portanto, esta alternativa é verdadeira.
O
foco principal situa-se no ponto médio do segmento
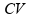
Verdadeira,
pois
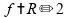 ,
sendo
,
sendo
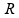 o valor do segmento
o valor do segmento
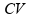 .
.
Os
focos secundários do espelho estão localizados sobre seu eixo
principal, na região delimitada pelo segmento
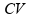 .
.
Um
dos focos está no segmento
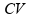 ,
mas o outro foco está simétricamente “fora” do espelho, logo
esta alternativa é falsa.
,
mas o outro foco está simétricamente “fora” do espelho, logo
esta alternativa é falsa.
Portanto, as alternativas 01), 02), 04) e 08) estão corretas.