UNESP-2017-Meio do ano

Universidade Estadual Paulista “Júlio de Mesquita Filho” (UNESP) é uma universidade pública brasileira, com atuação no ensino, na pesquisa e na extensão de serviços à comunidade. A instituição é uma das três universidades mantidas pelo governo do estado de São Paulo, ao lado da Universidade de São Paulo (USP) e da Universidade Estadual de Campinas (Unicamp).

A UNESP distingue-se das outras universidades estaduais por sua estrutura multicampi que abrange 24 municípios do estado – 21 campi no interior, um campus na cidade de São Paulo, um campus em São Vicente e um campus em Registro(estes 2 últimos campi tendo sido os primeiros de uma universidade pública no litoral paulista).1

Unesp foi a segunda colocada entre as universidades públicas no “VIII Prêmio Melhores Universidades”, presenteado anualmente pela publicação Guia do Estudante, da Editora Abril.  A Classificação Acadêmica das Universidades Mundiais (ARWU – sigla em inglês classificou a universidade entre as posições 301ª-400ª no mundo e entre as cinco melhores instituições de ensino superior do Brasil

01 – (UNESP-SP-017-Meio do ano)

Considere as seguintes características da moeda de R$ 0,10:

massa = 4,8 g; diâmetro = 20,0 mm; espessura = 2,2 mm.

(www.bcb.gov.br)

Admitindo como desprezível o efeito das variações de relevo sobre o volume total da moeda e sabendo que o volume de um cilindro circular reto é igual ao produto da área da base pela altura e que a área de um círculo é calculada pela fórmula πr², a densidade do material com que é confeccionada a moeda de R$ 0,10 é de aproximadamente

(A) 9 g/cm³.

(B) 18 g/cm³.

(C) 14 g/cm³.

(D) 7 g/cm³.

(E) 21 g/cm³.

02 – (UNESP-SP-017-Meio do ano)

Um gerador portátil de eletricidade movido a gasolina comum tem um tanque com capacidade de 5,0 L de combustível, o que garante uma autonomia de 8,6 horas de trabalho abastecendo de energia elétrica equipamentos com potência total de 1 kW, ou seja, que consomem, nesse tempo de funcionamento, o total de 8,6 kWh de energia elétrica. Sabendo que a combustão da gasolina comum libera cerca 3,2 × 10⁴ kJ/L e que 1 kWh = 3,6 × 10³ kJ, a porcentagem da energia liberada na combustão da gasolina que será convertida em energia elétrica é próxima de

(A) 30%.

(B) 40%.

(C) 20%.

(D) 50%.

(E) 10%.

03 – (UNESP-SP-017-Meio do ano)

No período de estiagem, uma pequena pedra foi abandonada, a partir do repouso, do alto de uma ponte sobre uma represa e verificou-se que demorou 2,0 s para atingir a superfície da água. Após um período de chuvas, outra pedra idêntica foi abandonada do mesmo local, também a partir do repouso e, desta vez, a pedra demorou 1,6 s para atingir a superfície da água.

(www.folharibeiraopires.com.br. Adaptado.)

Considerando a aceleração gravitacional igual a 10 m/s² e desprezando a existência de correntes de ar e a sua resistência, é correto afirmar que, entre as duas medidas, o nível da água da represa elevou-se

(A) 5,4 m.

(B) 7,2 m.

(C) 1,2 m.

(D) 0,8 m.

(E) 4,6 m.

04 – (UNESP-SP-017-Meio do ano)

Um homem sustenta uma caixa de peso 1000 N, que está apoiada em uma rampa com atrito, a fim de colocá-la em um caminhão, como mostra a figura 1. O ângulo de inclinação da rampa em relação à horizontal é igual a e a força de sustentação aplicada pelo homem para que a caixa não deslize sobre a superfície inclinada é , sendo aplicada à caixa paralelamente à superfície inclinada, como mostra a figura 2.

FIGURA1 FIGURA 2

(http://portaldoprofessor.mec.gov.br)

Quando o ângulo é tal que sen = 0,60 e cos = 0,80, o valor mínimo da intensidade da força F é 200 N. Se o ângulo for aumentado para um valor , de modo que sen = 0,80 e cos = 0,60, o valor mínimo da intensidade da força passa a ser de

(A) 400 N.

(B) 350 N.

(C) 800 N.

(D) 270 N.

(E) 500 N.

05 – (UNESP-SP-017-Meio do ano)

Observe o poema visual de E. M. de Melo e Castro.

(www.antoniomiranda.com.br. Adaptado.)

Suponha que o poema representa as posições de um pêndulo simples em movimento, dadas pelas sequências de letras iguais. Na linha em que está escrita a palavra pêndulo, indicada pelo traço vermelho, cada letra corresponde a uma localização da massa do pêndulo durante a oscilação, e a letra P indica a posição mais baixa do movimento, tomada como ponto de referência da energia potencial. Considerando as letras da linha da palavra pêndulo, é correto afirmar que

(A) a energia cinética do pêndulo é máxima em P.

(B) a energia potencial do pêndulo é maior em Ê que em D.

(C) a energia cinética do pêndulo é maior em L que em N.

(D) a energia cinética do pêndulo é máxima em O.

(E) a energia potencial do pêndulo é máxima em P.

06 – (UNESP-SP-017-Meio do ano)

No sistema auditivo humano, as ondas sonoras são captadas pela membrana timpânica, que as transmite para um sistema de alavancas formado por três ossos (martelo, bigorna e estribo). Esse sistema transporta as ondas até a membrana da janela oval, de onde são transferidas para o interior da cóclea. Para melhorar a eficiência desse processo, o sistema de alavancas aumenta a intensidade da força aplicada, o que, somado à diferença entre as áreas das janelas timpânica e oval, resulta em elevação do valor da pressão.

(www.anatomiadocorpo.com. Adaptado.)

Considere que a força aplicada pelo estribo sobre a janela oval seja 1,5 vezes maior do que a aplicada pela membrana timpânica sobre o martelo e que as áreas da membrana timpânica e da janela oval sejam 42,0 mm² e 3,0 mm², respectivamente. Quando uma onda sonora exerce sobre a membrana timpânica uma pressão de valor P_T, a correspondente pressão exercida sobre a janela oval vale

(A) 42 P_T

(B) 14 P_T

(C) 63 P_T

(D) 21 P_T

(E) 7 P_T

07 – (UNESP-SP-017-Meio do ano)

No centro de uma placa de madeira, há um orifício no qual está encaixada uma lente delgada convergente de distância focal igual a 30 cm. Esta placa é colocada na vertical e um objeto luminoso é colocado frontalmente à lente, à distância de 40 cm. No lado oposto, um espelho plano, também vertical e paralelo à placa de madeira, é disposto de modo a refletir a imagem nítida do objeto sobre a placa de madeira. A figura ilustra a montagem.

Nessa situação, o espelho plano se encontra em relação à placa de madeira a uma distância de

(A) 70 cm.

(B) 10 cm.

(C) 60 cm.

(D) 30 cm.

(E) 40 cm.

08 – (UNESP-SP-017-Meio do ano)

Um resistor ôhmico foi ligado a uma fonte de tensão variável, como mostra a figura.

Suponha que a temperatura do resistor não se altere significativamente com a potência dissipada, de modo que sua resistência não varie. Ao se construir o gráfico da potência dissipada pelo resistor em função da diferença de potencial U aplicada a seus terminais, obteve-se a curva representada em:

(A) (B) (C)

(D) (E)

09 – (UNESP-SP-017-Meio do ano)

O limite máximo de velocidade para veículos leves na pista expressa da Av. das Nações Unidas, em São Paulo, foi recentemente ampliado de 70 km/h para 90 km/h. O trecho dessa avenida conhecido como Marginal Pinheiros possui extensão de 22,5 km. Comparando os limites antigo e novo de velocidades, a redução máxima de tempo que um motorista de veículo leve poderá conseguir ao percorrer toda a extensão da Marginal Pinheiros pela pista expressa, nas velocidades máximas permitidas, será de, aproximadamente,

(A) 1 minuto e 7 segundos.

(B) 4 minutos e 33 segundos.

(C) 3 minutos e 45 segundos.

(D) 3 minutos e 33 segundos.

(E) 4 minutos e 17 segundos.

10 – (UNESP-SP-017-Meio do ano)

As pás de um gerador eólico de pequeno porte realizam 300 rotações por minuto. A transformação da energia cinética das pás em energia elétrica pelo gerador tem rendimento de 60%, o que resulta na obtenção de 1 500 W de potência elétrica.

(http://ambiente.hsw.uol.com.br. Adaptado.)

Considerando π = 3, calcule o módulo da velocidade angular, em rad/s, e da velocidade escalar, em m/s, de um ponto P situado na extremidade de uma das pás, a 1,2 m do centro de rotação. Determine a quantidade de energia cinética, em joules, transferida do vento para as pás do gerador em um minuto. Apresente os cálculos.

11 – (UNESP-SP-017-Meio do ano)

A figura 1 mostra um cilindro reto de base circular provido de um pistão, que desliza sem atrito. O cilindro contém um gás ideal à temperatura de 300 K, que inicialmente ocupa um volume de 6,0 × 10^-3 m³ e está a uma pressão de 2,0 × 10⁵ Pa.

O gás é aquecido, expandindo-se isobaricamente, e o êmbolo desloca-se 10 cm até atingir a posição de máximo volume, quando é travado, conforme indica a figura 2.

Considerando a área interna da base do cilindro igual a 2,0 × 10^-2 m², determine a temperatura do gás, em kelvin, na situação da figura 2. Supondo que nesse processo a energia interna do gás aumentou de 600 J, calcule a quantidade de calor, em joules, recebida pelo gás. Apresente os cálculos.

12 – (UNESP-SP-017-Meio do ano)

O mecanismo de formação das nuvens de tempestade provoca a separação de cargas elétricas no interior da nuvem, criando uma diferença de potencial elétrico U entre a base da nuvem e o solo. Ao se atingir certo valor de potencial elétrico, ocorre uma descarga elétrica, o raio.

(http://pt.wikipedia.org. Adaptado.)

Suponha que, quando a diferença de potencial entre a nuvem e o solo atingiu o valor de 1,8 × 10⁸ V, ocorreu um raio que transferiu uma carga elétrica de 30 C, em módulo, da nuvem para o solo, no intervalo de 200 ms. Calcule a intensidade média da corrente elétrica, em ampères, estabelecida pelo raio. Considerando que uma bateria de capacidade 50 A · h acumula energia para fornecer uma corrente de 50 A durante uma hora, calcule quantas baterias de 10 V e capacidade 50 A · h poderiam ser totalmente carregadas supondo que toda a quantidade de energia desse raio pudesse ser transferida a elas. Apresente os cálculos.

RESPOSTAS

01 – O exercício mesmo nos dá a direção que precisamos seguir, vamos utilizar a fórmula da densidade:

d =

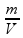
Aonde:

d é a densidade

m é a massa

V é o volume

A massa é dada, porém falta o volume. Temos que modelar a moeda como se fosse um cilindro:

Volume do cilindro:

V = área da base X altura (a altura é a espessura e área da base é dada)

Nossa moeda V =

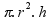
Substituindo na fórmula da densidade:

d =

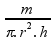
O exercício fornece o diâmetro, então precisamos substituir o r por D (diâmetro). Sabemos que o diâmetro é metade do raio:

r =

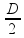
Portanto o raio ao quadrado:

r² =

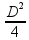
Temos então a fórmula final da densidade:

d =

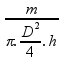
O diâmetro é dado em mm passando para cm basta dividir por 10:

D = 2 cm

O mesmo para a altura ou espessura:

h = 0,22

Calculando (podemos deixar as medidas em gramas e cm³, visto que o resultado final está representado nessas medidas):

d =

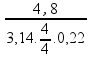
d = 6,94 g/cm³ (alternativa D)

02 – Esse exercício assusta de primeira, mas vamos com calma. Vamos começar calculando quanto de energia será gerada pela combustão. Essa energia representa o quanto de energia que será consumida para se produzir a energia elétrica desejada. A gasolina libera 3,2.10⁴ kJ/L, temos 5 L de gasolina, portanto:

3,2.10⁴.5 = 16.10⁴ kJ de energia total

Agora que sabemos a energia total e o exercício nos forneceu a energia convertida em elétrica, apenas precisamos calcular a porcentagem, ou seja, o rendimento:

rendimento =

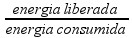
Precisamos calcular a energia liberada. Como 1 kWh = 3,6.10³ kJ, então 8,6 kWh:

3,6.10³.8,6 = 30,96.10³ kJ = 3,096.10⁴ kJ

Substituindo na equação do rendimento:

rendimento =

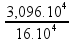
rendimento = 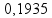= 19,35% (alternativa C)

03 – Nesse exercício precisamos apenas calcular a altura em ambos os casos e comparar:

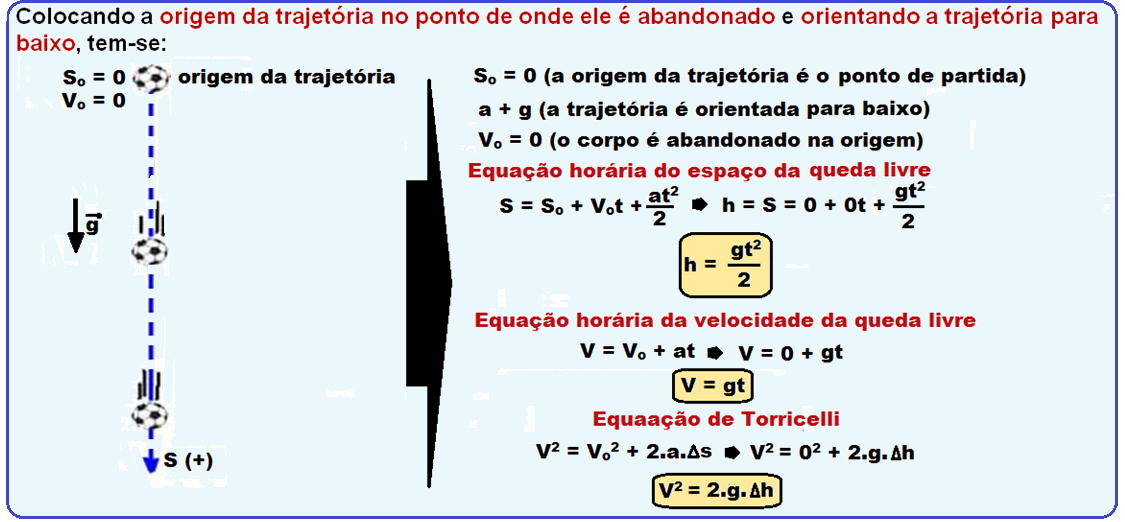
Como explicado acima, o ponto de partida é zero e sua velocidade inicial também. Sendo assim a equação horária é reduzida para:

h =

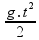
Aonde:

h é a altura da queda (ou S que seria o deslocamento final)

g é a aceleração da gravidade

t é o tempo da queda

Calculando para a época de estiagem (t = 2 s):

Calculando o outro caso (t = 1,6 s):

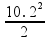h = h =

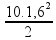
h = 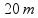h = 12,8 m

Calculando a diferença:

20 – 12,8 = 7,2 m (alternativa B)

04 – É o exercício mais difícil até agora, vamos por partes:

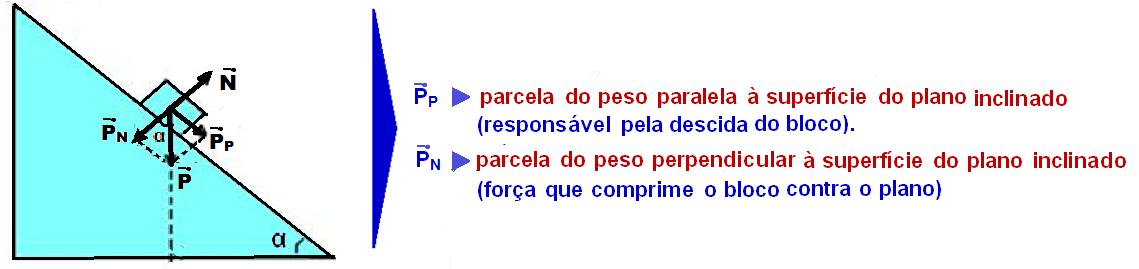
Observando a imagem acima é preciso destacar algumas coisas. Para se manter a caixa parada na rampa é necessário uma força de intensidade igual à 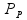, porém com sentido contrário. Já que estamos em um plano inclinado com atrito, já temos uma força contrária ao 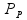a própria força de atrito.

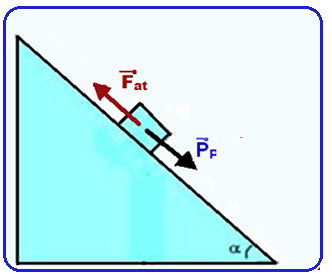
Ou seja a força que o homem deve executar somada com a força de atrito devem ser iguais à :

=

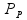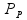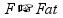
Aonde:

F é a força exercida pelo homem

Fat é a força de atrito

Agora que sabemos dessa relação, podemos calcular a força de atrito no primeiro caso. Observe que o exercício nos forneceu F nesse caso, mas para calcularmos Fat ainda precisamos encontrar P_P:

A imagem acima explica como encontrá-lo usando o triângulo retângulo. Esse sen é equivalente ao seno dado no plano. Substituinto na fórmula acima, aonde P é o peso da nossa caixa:

P_P = P.sen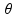

P_P = 1000.0,6

P_P = 600 N

Agora que sabemos P_P, podemos calcular a força de atrito:

Fat = P_P – F

Fat = 600 – 200

Fat = 400 N

Precisamos desse Fat para calcularmos o coeficiente de atrito da superfície, a fórmula é apresentada abaixo:

Aonde:

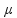é o coeficiente de atrito

Isolando o coeficiente:

=

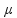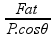
Substituindo:

=

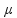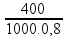
Calculando:

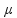= 0,5

Agora que encontramos o coeficiente de atrito podemos passar para o segundo plano, lembrando que esse coeficiente é o mesmo em ambos os casos visto que o material da rampa é o mesmo. Vamos começar pela força de atrito:

Fat = 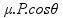(nesse caso o cos é 0,6)

Substituindo:

Fat =

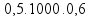
Calculando:

Fat =

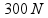
Sabendo da força de atrito, só nos resta achar P_p:

P_P = P.sen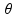 (nesse caso o seno é 0,8)

P_P = 1000.0,8

P_P = 800 N

Agora que sabemos as duas forças:

=

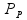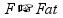
Isolando F:

F = P_P – Fat

Substituindo:

F = 800 – 300

F = 500 N (alternativa E)

05 – Vamos analisar todas as afirmações:

A letra A de cara já é a correta, pois a energia cinética é máxima nos pontos onde a energia potencial é mínima, pois toda essa energia foi justamente transformada em cinética.

A B está errada porque como o ponto N está lozalizado em um ponto mais alto, ele possui uma energia potencial maior, pelo mesmo raciocínio apresentado na justificativa anterior. O mesmo raciocínio explica o motivo da afirmação C estar errada também.

Em D o correto seria a energia cinética é mínima, pois o movimento parte dele.

Em E a energia potencial é mínima, visto que a altura é mínima.

06 – Esse exercício apresenta a relação entre força,área e pressão de uma forma interessante. Vamos aos cálculos:

Como podemos ver pressão é a força exercida em uma determinada área. Sabemos que a área da janela oval é 14 vezes menor que a da membrana timpânica, sendo assim a pressão exercida deve ser 14 vezes maior, por a área e a pressão serem inversamente proporcionais. Agora observe também que a força exercida na janela oval é 1,5 vezes maior, como a força e a pressão são diretamente proporcionais, então temos que a pressão é:

14.1,5 = 21 vezes maior (alternativa D)

07 – Para esse exercício precisamos da fórmula a seguir:

Substituindo na fórmula:

=

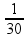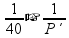
Isolando P´:

=

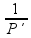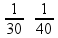
Calculando:

=

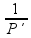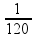
Ou seja:

P´ = 120 cm

Para que a imagem seja refletida de forma visível na caixa o espelho deve se encontrar na metada da distância aonde quer se projetar a imagem e sua imagem, portanto o espelho deve ser localizado 60 cm após a placa de madeira. Essa relação se dá justamente por questões de simetria, visto que o espelho reflete exatamente a imagem.

08 – Para conseguirmos resolver exercício precisamos encontrar a equação que é responsável por esse gráfico. Precisamos de uma relação que expresse P em função de U:

Como podemos perceber a potência é proporcional ao quadrado do diferencial, sendo assim o gráfico deve ser uma parábola, excluímos as alternativas B, D e E. Como é uma relação diretamente proporcional, então quanto maior o P, maior o U. Sendo asssim a alternativa correta é a C.

09 – Apenas precisamos calcular os dois casos e compará-los.

Isolando o tempo:

=

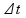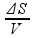
Substituindo:

= =

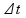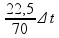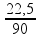
Calculando:

= =

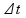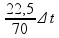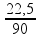
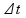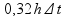= = 0,25

Calculando a diferença de tempo:

=

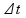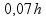
Transformando em min (multiplicando por 60):

4,2 min = 4 min 12 segundos (alternativa E)

10 – Para encontrarmos a velocidade angular primeiro precisamos encontrar o número de rotações por segundo (frequência). Como temos rotações por minuto, basta então dividir por 60:

f = 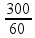= 5 voltas/s = 5 Hz

Como cada volta tem o valor de 2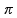, então: (essa forma é similar à = )

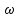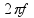5. 2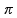 = 10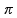 rad/s (velocidade angular)

Como 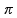= 3:

10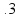 rad/s = 30 rad/s (velocidade angular)

Abaixo segue uma relação entre velocidade angular e escalar:

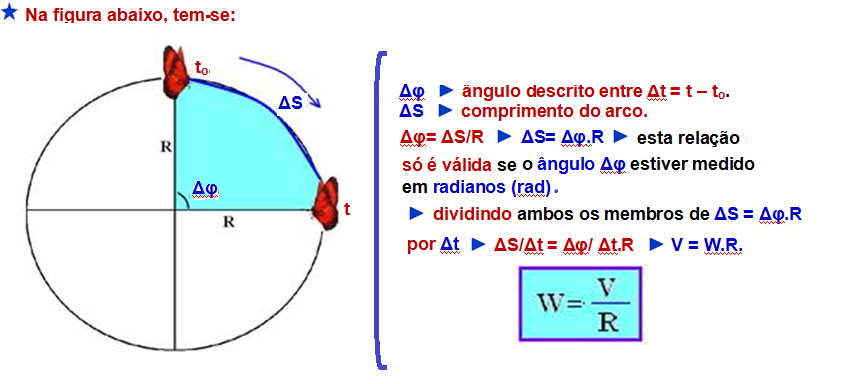
Observe que para obtermos a velocidade escalar a partir de 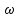basta multiplicar pelo raio (V = 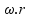), o que faz todo o sentido, já que na angular só é considerado o número de voltas, então para se obter a distância basta multiplicar esse número de voltas (2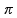) pelo tamanho (r), formando (2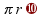 que é o raio do círculo.

Multiplicando a velocidade angular por r:

V = 30.1,2 = 36 m/s (velocidade escalar)

Para encontrarmos a potência total, aquela que o vento exerce na pá para que ela gire gerando energia elétrica, precisamos da relação abaixo. Essa potência é importante para encontrarmos a quantidade de energia cinética que o vento exerce na pá:

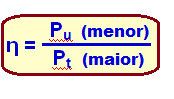
Aonde:

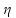é o rendimento

P_u é a potência gerada

P_t é a potência utilizada para gerar P_u

Isolando P_t:

P_t =

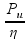
Substituindo:

P_t =

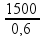
Calculando:

P_t = 2500 W

Ou seja, foram necessários 2500 W de potência originada pelo fluxo do vento para gerar 1500 W de potência elétrica. Agora que sabemos a potência precisamos encontrar a energia cinética, para isso:

Aonde:

P é a potência

W é o trabalho, também pode ser usado E de energia

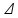t é a variação de tempo

Utilizando energia ao invés de trabalho e isolado-a:

E = P.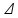t

Substituindo:

E = 2500.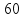 (já que estamos calculando para um minuto)

Calculando:

E = 150000 J = 1,5.10⁵ J (Energia cinética originada do vento)

11 – Para calcularmos a temperatura final precisamos primeiro do volume final. Podemos calcular visto que sabemos que o o êmbolo se deslocou 10 cm:

Volume inicial = 6.10^-3 m³

Volume final = Volume inical + 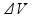(volume com 10 cm de deslocamento)

Passando 10 cm para metros (dividir por 100):

10 cm = 0,1 m

Calculando o :

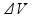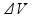= área interna X deslocamento

Substituindo:

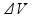= 2.10^-2.0,1

Calculando:

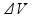= 2.10^-3 m³

Agora calculando o volume final:

Volume final = 6.10^-3 + 2.10^-3

Volume final = 8.10^-3 m³

Sabendo o volume final podemos utilizar a fórmula a seguir, já que se trata de um gás ideal:

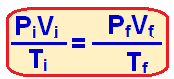
Aonde:

P_i e P_f é a pressão inicial e final

V_i e V_f é o volume inicial e final

T_i e T_f é a temperatura inicial e final

Como é uma expansão isobárica (pressão constante) podemos cortar a pressão em ambos os lados, restando apenas:

=

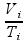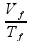
Substituindo:

=

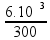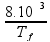
Isolando a temperatura final:

T_f =

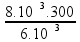
Calculando:

T_f = 400 K (temperatura final)

Achamos a temperatura, agora vamos para a segunda parte do exercício. Para calcularmos a quantidade de calor vamos utilizar a primeira lei da termodinâmica. Como se trata de uma transformação isobárica:

Como a pressão é constante o nosso trabalho só depende da variação do volume:

W = P.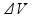

Substituindo. Nós calculamos a variação anteriormente (2.10^-3):

W = 2.10⁵. 2.10^-3

Calculando:

W = 4.10² J

O exercício já nos forneceu a variação de energia interna (600 J). Vamos então substituir na equação da primeira lei:

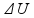= Q – W

Isolando a quantidade de calor:

Q = 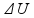+ W

Substituindo:

Q = 600 + 400

Calculando:

Q = 1000 J (quantidade de calor)

12 – Esse exercício assusta, mas na verdade ele é mais fácil que parece, vamos aos poucos. Primeiramente ele pergunta a intensidade média, que não é nada mais que a quantidade de carga transferida em determinado tempo:

Substituindo. Lembre-se que o tempo está em ms = 1.10^-3 s, portanto 200 ms = 0,2 s:

i =

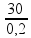
Calculando:

i = 150 A (intensidade média)

Já calculamos a intensidade média. Agora vamos para a segunda parte do exercício. Precisamos primeiramente calcular quanto de energia será fornecido por esse raio (Energia total):

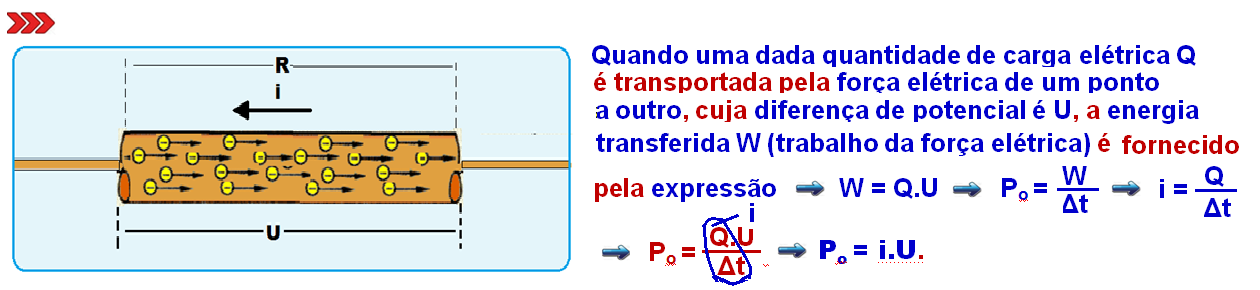
Ou seja:

W = Q.U ou E = Q.U (No caso o trabalho é a variação de energia, como a energia se mantém constante durante o raio então W = E)

Substituindo:

E = 30.1,8.10⁸

E = 54.10⁸ J

Agora que sabemos a energia total precisamos calcular a energia de cada bateria, vamos utilizar o mesmo procedimento. A bateria tem uma carga de 50 A.h, como 1 hora = 3600 s:

Q_Bateria = 50.3600 = 180000 J (carga total da bateria)

Sabendo a carga, podemos substituir na equação:

E_Bateria = Q_Bateria.U_Bateria

E_Bateria = 1,8.10⁵.10

Calculando:

E_Bateria = 1,8.10⁶ J (energia total de cada bateria)

Como sabemos a energia total e a de cada bateria, basta dividir uma pela outra e encontrar o número de baterias possíveis:

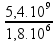= 3.10³ baterias (número de baterias totalmente carregadas)