

A Faculdade de Medicina de São José do Rio Preto (FAMERP) é uma faculdade pública paulista, fundada em 1968.
É uma das 6 faculdades estaduais de Medicina de São Paulo e seu curso médico é ministrado no sistema tradicional.
Uma das mais bem conceituadas faculdades de Medicina e Enfermagem do país, se destaca por possuir o segundo maior hospital-escola do Brasil, o Hospital de Base de São José do Rio Preto, que perde apenas para o Hospital das Clínicas de São Paulo.
O Hospital de Base, tem instalações de aproximadamente 720 leitos. Mensalmente, o hospital realiza aproximadamente 4,5 mil internações e 2.600 cirurgias, além dos 35.000 atendimentos ambulatoriais e 12 mil atendimentos de emergência.
Em 2008, ganhou o prêmio nacional Guia do Estudante / Banco Real de Melhor Faculdade do Interior.
Ainda em 2008, recebeu nota máxima no Índice Geral de Cursos (IGC) promovido pelo MEC, classificando-se como a segunda melhor instituição pública do país, atrás apenas do ITA2 . No IGC 2009, divulgado no início de 2011, novamente a faculdade recebeu nota máxima do MEC .
A Comissão Permanente para o Vestibular (Comvest) da UNICAMP, era quem realizava a seleção para os cursos Medicina e Enfermagem da FAMERP até o ano de 2013, num sistema integrado ao vestibular da UNICAMP. Hoje esse processo é realizado pela VUNESP tendo agora a instituição o seu próprio processo seletivo.
Conhecimentos Gerais
01-(FAMERP-SP-017)


02-(FAMERP-SP-017)


Um desodorante é vendido em duas embalagens de tamanhos diferentes, porém de formatos matematicamente semelhantes.
A figura indica algumas das medidas dessas embalagens.
Se a capacidade da embalagem maior é de 100 mL, a capacidade da embalagem menor é de
(A) 64,0 mL.
(B) 48,6 mL.
(C) 56,4 mL.
(D) 80,0 mL.
(E) 51,2 mL.
03-(FAMERP-SP-017)

Uma bola rola sobre uma bancada horizontal e a abandona, com velocidade Vo, caindo até o chão.
As
figuras
representam a visão de cima e a visão de frente desse movimento,
mostrando
a bola
em instantes diferentes durante sua queda, até o momento em que ela
toca o solo.
Desprezando a resistência do ar e considerando as informações das figuras, o módulo de Vo é igual a
(A) 2,4 m/s. (B) 0,6 m/s. (C) 1,2 m/s.
(D) 4,8 m/s. (E) 3,6 m/s.
04-(FAMERP-SP-017)

O pai de uma criança pretende pendurar, no teto do quarto de seu filho, um móbile constituído por:
seis
carrinhos de massas iguais,
distribuídos em dois
conjuntos, A e B; duas hastes rígidas de
massas
desprezíveis,
com marcas
igualmente espaçadas;
e fios
ideais.

O conjunto A já está preso a uma das extremidades da haste principal do móbile.
Sabendo que o móbile será pendurado ao teto pelo ponto P, para manter o móbile em equilíbrio, com as hastes na horizontal, o pai da criança deverá pendurar o conjunto B, na haste principal, no ponto (A) 5.
(B) 1.
(C) 4.
(D) 3.
(E) 2.
05-(FAMERP-SP-017)

Em
uma exibição
de acrobacias aéreas,
um avião
pilotado
por uma pessoa
de 80 kg
faz manobras e deixa no
ar um rastro de fumaça indicando sua trajetória.
Na figura, está representado um looping circular de raio 50 m contido em um plano vertical, descrito por esse avião.
Adotando g = 10 m/s2 e considerando que ao passar pelo ponto A, ponto mais alto da trajetória circular, a velocidade do avião é de 180 km/h, a intensidade da força exercida pelo assento sobre o piloto, nesse ponto, é igual a (A) 3 000 N.
(B) 2 800 N.
(C) 3 200 N.
(D) 2 600 N.
(E) 2 400 N.
06-(FAMERP-SP-017)

Durante uma partida de sinuca, um jogador, impossibilitado de atingir diretamente a bola vermelha
com
a bola
branca, decide
utilizar
a tabela da mesa. Ele
dá uma tacada
na bola branca, que,
seguindo a trajetória
tracejada indicada na figura, com
velocidade
escalar constante de módulo v, acerta a bola vermelha.
Sendo m a massa da bola branca, o módulo da variação da quantidade de movimento sofrida por essa bola na colisão contra a tabela da mesa foi igual a
(A)
mv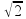
(B) zero
(C) mv
(D) 2mv
(E)
mv

08-(FAMERP-SP-017)


Dois raios de luz monocromáticos provenientes do ar, um azul e o outro vermelho, incidem no ponto
P da superfície de uma esfera maciça de centro C, paralelos um ao outro, na direção da linha tracejada indicada na figura.
A esfera é feita de vidro transparente e homogêneo.
Se o índice de refração absoluto do vidro é maior para a cor azul do que para a vermelha e se não houve reflexão total dentro da esfera, a figura que representa corretamente a trajetória desses raios desde a sua incidência no ponto P até a sua emergência da esfera está indicada em

09-(FAMERP-SP-017)

Dois pulsos transversais, 1 e 2, propagam-se por uma mesma corda elástica, em sentidos opostos, com velocidades escalares constantes e iguais, de módulos 60 cm/s.
No instante t = 0, a corda apresenta-se com a configuração representada na figura 1.
Após a superposição desses dois pulsos, a corda se apresentará com a configuração representada na figura 2.

Considerando a superposição apenas desses dois pulsos, a configuração da corda será a representada na figura 2, pela primeira vez, no instante
![]()
10-(FAMERP-SP-017)

Quatro cargas elétricas puntiformes, Q1, Q2, Q3 e Q4, estão fixas nos vértices de um quadrado, de modo que |Q1| = |Q2| = |Q3| = |Q4|.

As posições das cargas e seus respectivos sinais estão indicados na figura.
Se E for o módulo do campo elétrico no ponto P, centro do quadrado, devido à carga Q1, o campo elétrico resultante no ponto P, devido à presença das quatro cargas, terá módulo
![]()
11-(FAMERP-SP-017)

A
figura
representa
o esquema
de ligação dos faróis de um automóvel à bateria do veículo.
O circuito é constituído por: duas lâmpadas de 12 V – 60 W cada uma; uma chave de acionamento e um fusível de proteção, ambos de resistências desprezíveis; e fios de ligação e conectores, também ideais.
Se os dois faróis estiverem acesos, das opções indicadas nas alternativas, aquela que corresponde à menor amperagem do fusível capaz de proteger esse circuito é
(A) 15 A.
(B) 12 A.
(C) 6 A.
(D) 4 A.
(E) 9 A.
12-(FAMERP-SP-017)

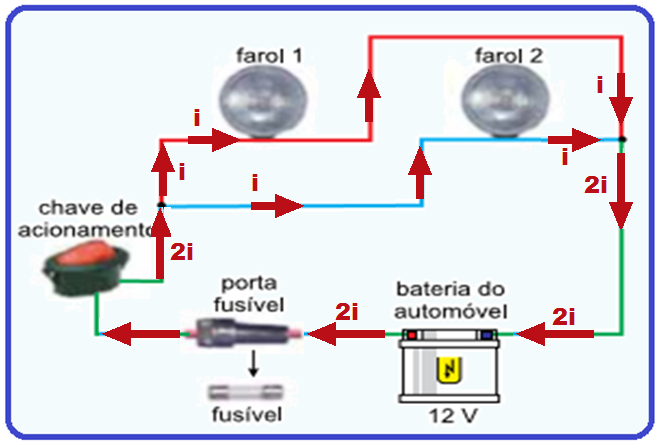
Uma
espira
metálica retangular ABCD,
de área
constante,
está totalmente
imersa em
um campo
magnético uniforme horizontal criado
na região entre dois
polos magnéticos norte e sul, como
representado na
figura. 
Inicialmente, a espira está em repouso em um plano vertical perpendicular às linhas de indução do campo magnético.
Suponha que a espira gire 90º no sentido anti-horário, em torno de um eixo vertical, nesse campo magnético. Enquanto isso acontece,
(A) circulará por ela uma corrente elétrica induzida sempre no sentido DCBA.
(B) circulará por ela uma corrente elétrica induzida, primeiro no sentido DCBA e depois no sentido ABCD. (C) circulará por ela uma corrente elétrica induzida sempre no sentido ABCD.
(D) circulará por ela uma corrente elétrica induzida, primeiro no sentido ABCD e depois no sentido DCBA. (E) não circulará por ela corrente elétrica induzida.
Conhecimentos específicos
01-(FAMERP-SP-017)

Um corpo de massa 8 kg movimenta-se em trajetória retilínea sobre um plano horizontal e sua posição (s) e sua velocidade escalar (v) variam em função do tempo (t), conforme os gráficos.

a) Determine a posição x, em metros, desse corpo no instante t = 10 s.
b) Calcule o módulo da resultante das forças, em newtons, que atuam sobre o corpo no intervalo de tempo entre t = 6 s e t = 12 s.
02-(FAMERP-SP-017)

A figura representa um satélite artificial girando ao redor da Terra em movimento circular e uniforme com período de rotação de 140 minutos.

O gráfico representa como varia o módulo da aceleração da gravidade terrestre para pontos situados até uma distância 2R do centro da Terra, onde R = 6 400 km é o raio da Terra.
Considere a Terra perfeitamente esférica e as informações contidas na figura e no gráfico.
a) Calcule o menor intervalo de tempo, em minutos, para que o satélite se movimente da posição A para a posição B.
b) Determine o módulo da aceleração da gravidade terrestre, em m/s2, na posição em que se encontra o satélite.
03-(FAMERP-SP-017)

Uma caixa de massa 150 kg, com faces retangulares pintadas nas cores verde, vermelho e azul, está apoiada na borda plana e horizontal de uma piscina, sobre uma de suas faces azuis, conforme a figura 1, que também indica as dimensões de cada uma das faces da caixa.
Na situação da figura 2, a caixa está dentro da piscina, totalmente submersa e apoiada no fundo, em repouso, sobre uma de suas faces verdes.

Considerando que a água da piscina esteja parada, que sua densidade seja igual a 103 kg/m3 e que
g = 10 m/s2, calcule, em pascal:
a) a pressão exercida pela caixa sobre a borda da piscina, na situação indicada na figura 1.
b) a pressão exercida pela caixa no fundo da piscina, na situação indicada na figura 2.
04-(FAMERP-SP-017)


05-(FAMERP-SP-017)

Uma calota esférica é refletora em ambas as faces, constituindo, ao mesmo tempo, um espelho côncavo e um espelho convexo, de mesma distância focal, em módulo.
A figura 1 representa uma pessoa diante da face côncava e sua respectiva imagem, e a figura 2 representa a mesma pessoa diante da face convexa e sua respectiva imagem.

a) Considerando as informações contidas na figura 1, calcule o módulo da distância focal desses espelhos.
b) Na situação da figura 2, calcule o aumento linear transversal produzido pela face convexa da calota.
06-(FAMERP-SP-017)

Uma lâmpada incandescente, de especificações técnicas 40 V – 25 W estabelecidas pelo fabricante, queima se for submetida a tensões acima da especificada.
Conforme
a figura,
essa
lâmpada
será instalada em um soquete ligado em série com o resistor R e
com
outros resistores que serão conectados entre os pontos A e B,
formando um circuito que será submetido a uma diferença de
potencial de 100 V.
Considerando que os fios e as conexões utilizados nesse circuito tenham resistências desprezíveis: a) determine a quantidade de carga elétrica, em coulombs, que atravessará a lâmpada se ela permanecer acesa, de acordo com suas especificações, durante 20 minutos.
b) indique o número máximo de resistores iguais, de 320 Ω cada um, que podem ser ligados em paralelo entre A e B, sem que a lâmpada queime.
Resolução comentada das questões de Física do vestibular da
FAMERP-2017
Conhecimentos Gerais
01- Como a vazão de água é constante, para um mesmo intervalo de tempo um mesmo volume de água está caindo no interior do copo.
Assim, quanto maior for a seção transversal do copo, o mesmo volume de água despejado em seu interior, no mesmo intervalo de tempo, provocará um aumento menor de altura e quanto menor for a seção transversal do copo, o mesmo volume de água despejado em seu interior, no mesmo intervalo de tempo, provocará um aumento maior de altura.
Observe atentamente o gráfico e a figura abaixo e veja que a alternativa que melhor satisfaz é a B.
R- B
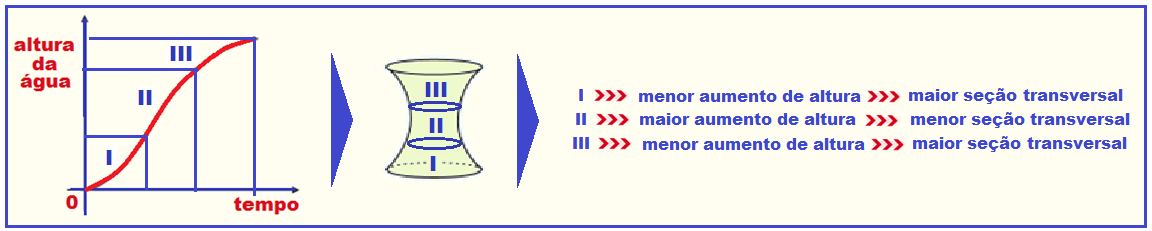
02- Sabendo que os recipientes de volumes Vmaior e Vmenor tem formatos matematicamente semelhantes seus volumes são proporcionais às qualquer uma de suas dimensões elevadas ao cubo.
Assim, são válidas as seguintes relações:
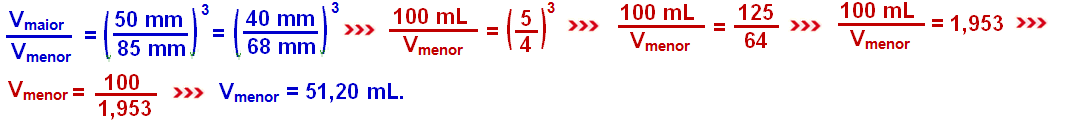
R- E
03- Como a bola sai da mesa com velocidade inicial (horizontal Vo) e cai sujeita à aceleração da gravidade g, trata-se de um lançamento horizontal.
Olhando de cima você está vendo o movimento horizontal da bola e olhando de frente, o movimento vertical da mesma.
Veja como a situação apresentada pode ser esquematizada (lançamento horizontal) com as seguintes características:
Colocando-se a origem do sistema de referência no ponto de lançamento, orienta-se, por exemplo, o eixo X para a direita e o eixo Y para baixo.
Decompõe-se o movimento em duas parcelas:
![]() Segundo
o eixo X
Segundo
o eixo X ![]() trata-se de um movimento
horizontal uniforme com
velocidade
constante de intensidade Vo
, que
é a velocidade
de lançamento
trata-se de um movimento
horizontal uniforme com
velocidade
constante de intensidade Vo
, que
é a velocidade
de lançamento
![]() S = So +
V.t
S = So +
V.t ![]() X
= 0 + Vo.t
X
= 0 + Vo.t
![]() X
= Vo.t
X
= Vo.t
![]() Segundo
o eixo Y
Segundo
o eixo Y ![]() trata-se de um movimento
uniformemente variado
com velocidade
inicial
trata-se de um movimento
uniformemente variado
com velocidade
inicial
Vo = 0, ou seja, é uma queda livre com o corpo abandonado da origem, sujeito apenas à aceleração da gravidade, de intensidade g, direção vertical e sentido para baixo.
Equações:
S
= So +
Vo.t
+ at2/2
![]() Y = 0 + 0.t + gt2/2
Y = 0 + 0.t + gt2/2 ![]() Y
= g.t2/2
Y
= g.t2/2
Vy =
Voy +
a.t ![]() Vy=
0 + g.t
Vy=
0 + g.t ![]() Vy
=
g.t
Vy
=
g.t
V2
= Vo2
+ 2.a.ΔS ![]() Vy2
= Voy2 +
2.g.Δh
Vy2
= Voy2 +
2.g.Δh ![]() Vy2
= 02 +
2.g.Δh
Vy2
= 02 +
2.g.Δh
![]() Vy2 =
2.g.Δh
Vy2 =
2.g.Δh
No caso do exercício:
Cálculo
do tempo t que a bola demora para atingir o solo onde y = 1,25 m
![]() Y
= g.t2/2
Y
= g.t2/2
![]() 1,25 =
1,25 =
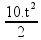
![]() t =
t =
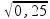
![]() t = 0,5 s.
t = 0,5 s.
Esse
tempo de queda na vertical é o mesmo que a bola demora para
percorrer X = 2,4 m na horizontal com velocidade Vo
![]() X = Vo.t
X = Vo.t
![]() 2,4 = Vo.0,5
2,4 = Vo.0,5
![]() Vo
= 4,8 m/s.
Vo
= 4,8 m/s.
R- D
04-
Peso
do conjunto A
![]() PA
= 4mg
PA
= 4mg
![]() peso do conjunto B
peso do conjunto B
![]() PB
= 2mg.
PB
= 2mg.
Chamando a distância entre cada marca consecutiva de d e de Y a distância de P até onde se deve colocar o peso PB você obterá o esquema da figura abaixo:
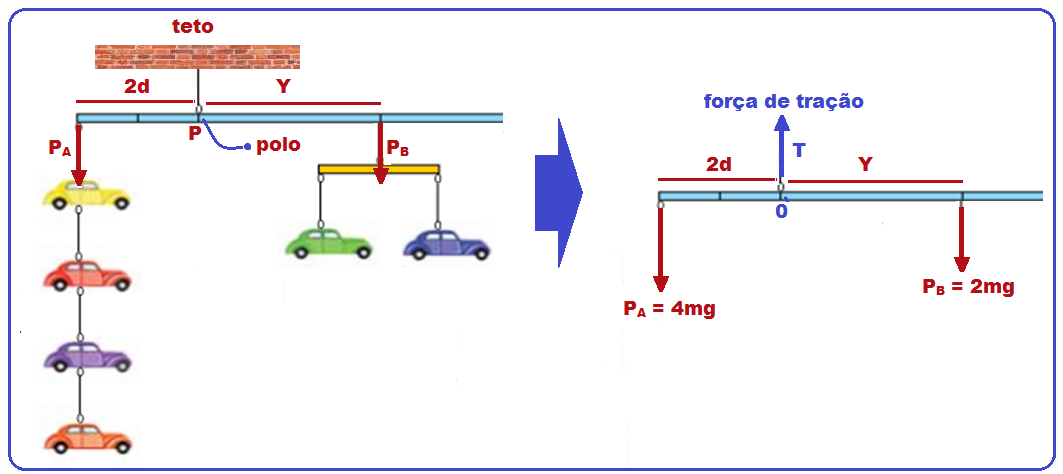
Adotando o ponto P como polo 0 (eixo de rotação) e o sentido horário de rotação como positivo e anti horário como negativo, vamos calcular o momento de cada força em relação ao polo.
MPA
= - F.dPAP
= - PA.2d
![]() MPA
= - 4mg2d
MPA
= - 4mg2d
![]() MPA
= - 8mgd
MPA
= - 8mgd
![]() (sinal negativo, pois tende a girar no sentido anti horário)
(sinal negativo, pois tende a girar no sentido anti horário)
MT
=
T.0
![]() MT
= 0
MT
= 0
MPB
= + F.dPPB
= + PB.Y
![]() MPB
= + 2mgY
MPB
= + 2mgY
![]() (sinal positivo, pois tende a girar no sentido horário)
(sinal positivo, pois tende a girar no sentido horário)
A
condição
de equilíbrio
de rotação é
que a soma
dos momentos de cada força em relação ao polo deve ser nula
![]() MPA
+ MT
+ MPB
= 0
MPA
+ MT
+ MPB
= 0
![]() - 8mgd + 0 + 2mgY = 0
- 8mgd + 0 + 2mgY = 0
![]() Y =
Y =
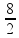
![]() Y
= 4
Y
= 4
R- C
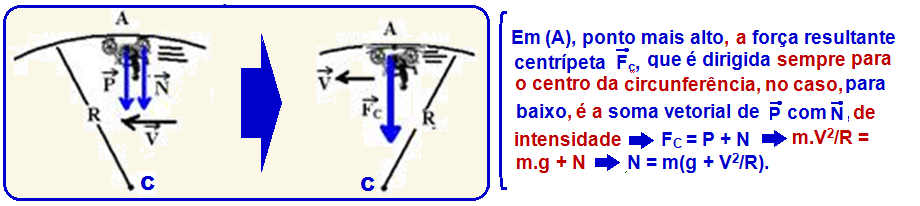
05-
Veja
a teoria
abaixo que está relacionada com o exercício onde
o avião
(ou o piloto) comportam-se como a moto e a normal
![]() que a moto troca com o piso do globo pela força que o avião troca
com o ar.
que a moto troca com o piso do globo pela força que o avião troca
com o ar.
Globo da morte
Suponha
um motociclista
de massa total m (massa dele + massa da moto) descrevendo
voltas segundo um plano
vertical, com velocidade
escalar constante ![]() no
interior de uma esfera metálica oca de raio R “globo da morte”.
no
interior de uma esfera metálica oca de raio R “globo da morte”.


06-
Interessa
a bola
branca de massa m com
quantidade
de movimento inicial
![]() e quantidade
de movimento final
e quantidade
de movimento final
![]() indicadas
na figura:
indicadas
na figura:
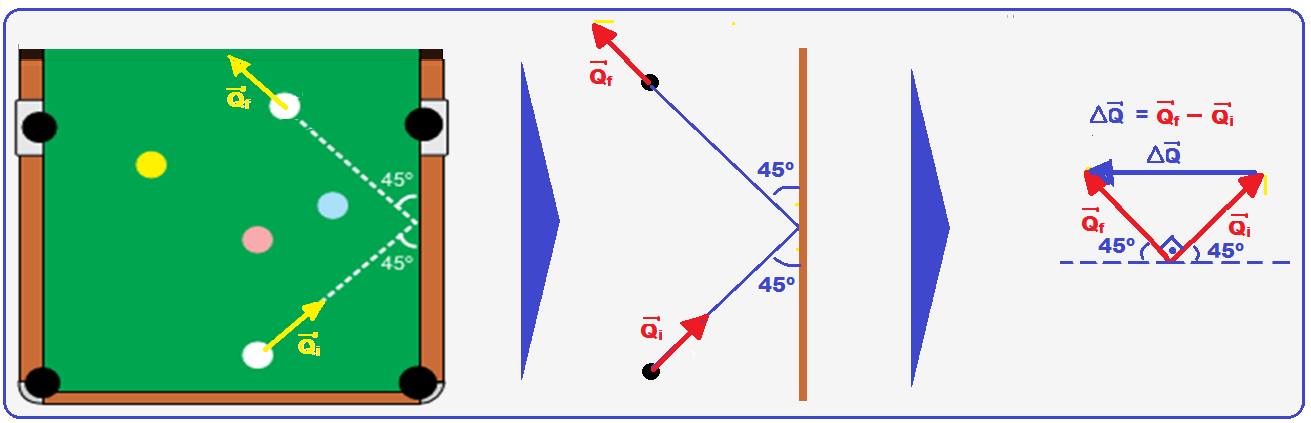

R- A
07-
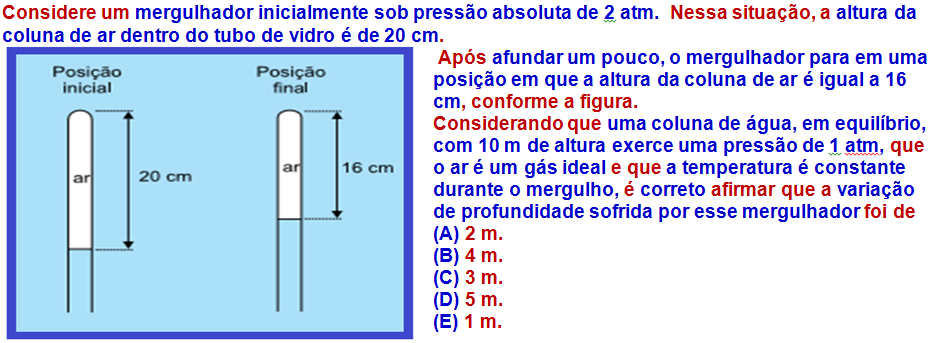
Como interessa o ar no interior do tubo vamos calcular seus volumes inicial (Vi) e final (Vf) sendo (S) a área da vase do cilindro, que é a mesma nas duas situações:


Observe
que à
medida que ele afundou a pressão aumentou de 2,0 atm para 2,5 atm
sofrendo
um acréscimo
de
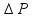 = 0,5 atm.
= 0,5 atm.
Como o enunciado considera que uma coluna de água, em equilíbrio, com 10 m de altura exerce uma pressão de 1,0 atm, ou seja, para cada 10m de aumento de profundidade a pressão aumenta de 1,0 atm então, como a pressão aumentou de 0,5 atm ele afundou 5,0 m.
R- D
08-
Índice de refração

Observe na expressão acima que, sendo a velocidade c da luz constante, a velocidade v de propagação da luz no meio (no caso, o vidro) é inversamente proporcional ao índice absoluto de refração da luz nesse meio.
A dispersão luminosa ocorre artificialmente quando a luz se dispersa como no interior de um prisma (ou no interior da esfera de vidro do exercício) ou quando passa do ar para a água, sendo mais desviada a luz monocromática violeta (menor velocidade) e menos desviada a luz monocromática vermelha (maior velocidade).
Como, pelo enunciado, o índice refração absoluto do vidro é maior para a cor azul do que para a
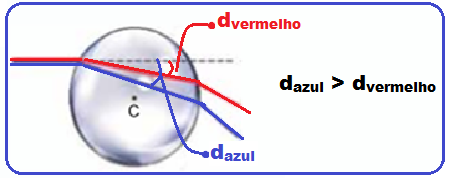
vermelha, a luz azul, no interior do vidro sofre maior desvio ao atravessar a esfera (veja figura acima).
R- B
09-
Observe
atentamente
nas figuras abaixo que a primeira
vez que o perfil da corda será como na figura 2 será
quando houver interferência
destrutiva do vale do pulso 1 (ponto A) com a crista do pulso 2
(ponto B) se anulando fornecendo o perfil de onda pedido e mostrado
pela linha preta..
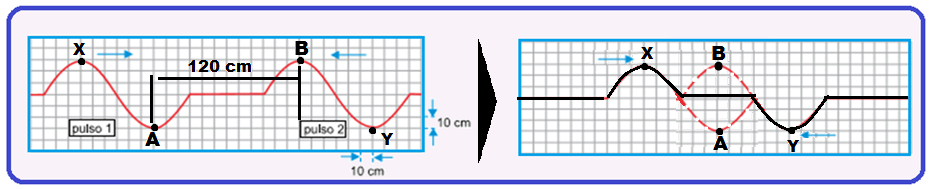
Assim,
cada
ponto A ou B, X ou Y deslocaram-se
de
 = 60 cm em sentidos contrários, cada um com velocidade
fornecida de V
= 60 cm/s tal
que V
=
= 60 cm em sentidos contrários, cada um com velocidade
fornecida de V
= 60 cm/s tal
que V
=
![]() 60 =
60 =
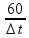
![]() ∆t
=
∆t
=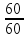 =
1 s
=
1 s
R- A
10- Lembre-se que cargas elétricas positivas criam no ponto P campos elétricos de afastamento e negativas, de aproximação.
Se
a intensidade
do campo elétrico criado por Q1
em P tem módulo E as
outras
cargas,
de mesmo
módulo,
também originarão
em P campos de intensidades E,
pois E =
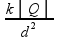 ,
com k,│Q│e
d2
constantes.
,
com k,│Q│e
d2
constantes.
Veja nas figuras a representação da direção e sentido dos campos criados em P por cada carga (positiva, de afastamento e negativa, de aproximação), e a sequência do cálculo da intensidade do campo elétrico resultante ER.
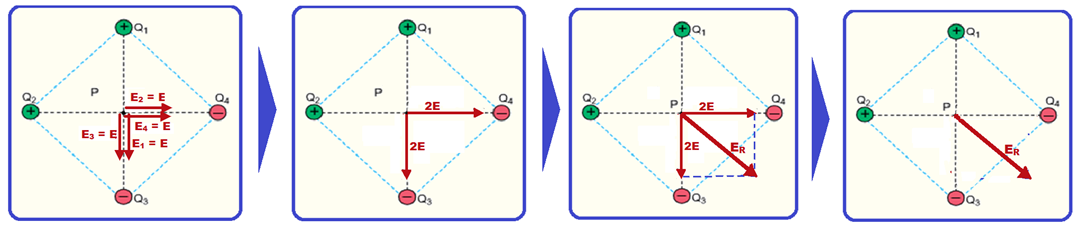
Aplicando
Pitágoras
na terceira figura (triângulo
retângulo)
![]() ER2
= (2E)2
+ (2E)2
=
2.(2E)2
ER2
= (2E)2
+ (2E)2
=
2.(2E)2
![]()
ER
=2.E.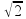
R- D
11- Observe que as duas lâmpadas acesas de mesma potência P = 60 W e sob tensão de U = 12 V estão associadas em paralelo e, ambas também em paralelo com a bateria de U = 12 V o que é óbvio, pois a tensão U é a mesma.
Assim,
usando os valores
nominais fornecidos
a corrente
elétrica i em cada lâmpada será a mesma e fornecida por P = i.U
![]() 60
= i.12
60
= i.12
![]() i = 5 A.
i = 5 A.
Veja
na figura
abaixo que
a corrente
que passa pelo fusível deve
valer if
=
2.i = 2.5
![]() if
= 10 A.
if
= 10 A.
Das alternativas, aquela cujo fusível apresenta menor amperagem (intensidade de corrente elétrica)
capaz de proteger esse circuito é o de 12 A.
R- B
12- As figuras abaixo representam a posição da espira num giro anti-horário de 0o a 90o da espira:
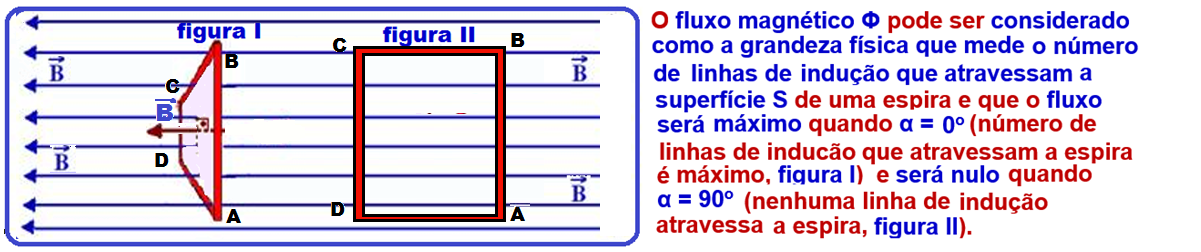 Aplicando
a regra
da mão direita na
situação
inicial
(figura I) “polegar
no sentido da corrente e
a
Aplicando
a regra
da mão direita na
situação
inicial
(figura I) “polegar
no sentido da corrente e
a
‘fechada’ da mão por dentro da espira no sentido de B” você verifica que o sentido inicial de i é ABCD.
À medida que a espira gira no sentido anti-horário a intensidade do fluxo magnético no interior da espira e consequentemente da corrente elétrica i vai diminuindo (mas mantendo o sentido ABCD) até completar o giro de 90o (figura II) quando se anulam.
R- C
Conhecimentos específicos
01-
a) Em
todo
gráfico Vxt o deslocamento
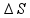 do
corpo é numéricamente
igual á área,
nesse
caso, entre
os
instantes
0 e 10 s que é a área de um trapézio:
do
corpo é numéricamente
igual á área,
nesse
caso, entre
os
instantes
0 e 10 s que é a área de um trapézio:

Mas, o enunciado não pede o deslocamento entre 0s e 10s, mas sim a posição no instante t = 10 s

e,
pelo
gráfico Sxt
você observa que
ele partiu
da origem So
= 0, então
quando
t = 10s o espaço S será
![]()
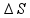 = S – So
= S – So
![]() 26 = S – 0
26 = S – 0
![]() S
= 26 m.
S
= 26 m.
b)
Observe
no gráfico
da velocidade que,
entre 5s
e 10 s o gráfico é uma mesma reta inclinada o
que significa
que nesse intervalo de tempo a aceleração tem o mesmo módulo
que pode ser calculado
por a
=
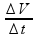 =
=
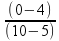
![]() a
= -
a
= -
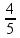
![]() em
módulo
em
módulo
![]() a = 0,8 m/s2.
a = 0,8 m/s2.
Pelo
Princípio
Fundamental da Dinâmica
ou Segunda
lei de Newton ![]() FR
= m.a =
8.0,8
FR
= m.a =
8.0,8
![]()
FR = 6,4 N.
02-
a) O menor intervalo de tempo, em minutos, para que o satélite se movimente da posição A para a posição B, ocorre quando o satélite se move no sentido anti-horário varrendo o ângulo de 108o.
Pelo enunciado, o período do satélite (tempo que ele demora para efetuar uma volta completa em torno da Terra e percorrer um arco de 360o) é de 140 min, então para percorrer 108o basta utilizar uma regra de três:
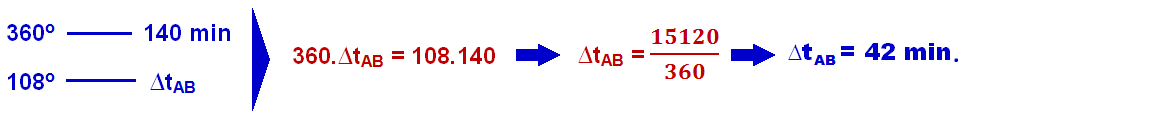
b)
O
raio
da órbita do satélite (Ro)
é
medido
em relação ao centro da Terra, ou
seja Ro
= RT
+ 2560
![]() Ro
= 6400 + 2650
Ro
= 6400 + 2650
![]() Ro
= 8960 km.
Ro
= 8960 km.
Assim,
o satélite
dista do centro da Terra em
função
ao raio da Terra R
de
![]() Ro
=
Ro
=
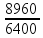 =
1,4R.
=
1,4R.
Veja no gráfico a correspondência entre essa distância (Ro =1,4R) e g:
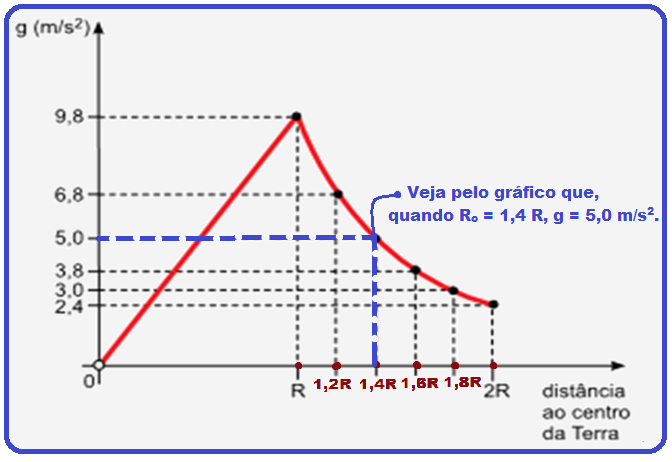
R - g = 5m/s2
03- a)
A
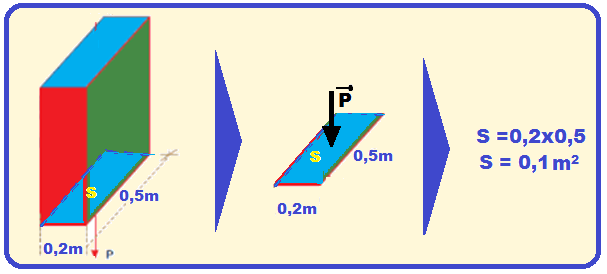
força responsável pela pressão sobre a área S = 0,1 m2
é o peso da caixa de módulo P = m.g = 150x10
![]() P = 1500N.
P = 1500N.
Pressão
exercida pela caixa sobre a borda da piscina
![]() PR
=
PR
=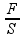 =
=
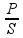 =
=
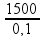
![]() PR
= 15000 = 15000 N/m2
PR
= 15000 = 15000 N/m2
![]() PR
= 15 kPa.
PR
= 15 kPa.
b):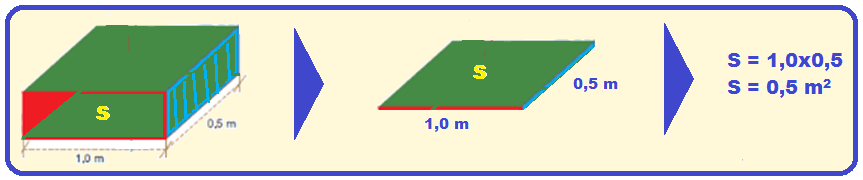
Agora, com a caixa em repouso na superfície do fundo da piscina a nova área apoiada será S = 0,5 m2.
O volume da caixa vale Vcaixa = 1,0x0,5x0,2 = 0,1 m3.
Como
a caixa está totalmente
imersa na água ela
sofrerá um empuxo E, vertical
e para cima,
de intensidade E = dágua.Vcaixa.g
= 103.10-1.10
![]() E
= 103
N.
E
= 103
N.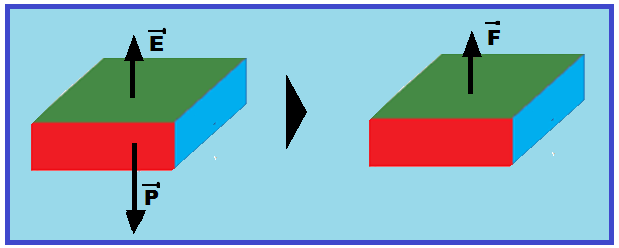
Além do empuxo age sobre a caixa seu peso P, vertical e para baixo de intensidade P = 1500 N.
Assim, a intensidade da força que a caixa aplica sobre o fundo da piscina na área de contato vale
FR
= P – E = 1500 – 1000
![]() FR
= 500 N.
FR
= 500 N.
PR
=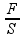 =
=
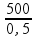 =
1000 N/m2
=
1000 N/m2
![]() PR
= 1 kPa.
PR
= 1 kPa.
04-
a)

São dados:
Q1
![]() quantidade
de calor recebido
da fonte
quente num ciclo
quantidade
de calor recebido
da fonte
quente num ciclo
![]() Q1
= 4,0.103
J
Q1
= 4,0.103
J
Q2
![]() quantidade
de calor rejeitado
para a fonte
fria num ciclo
quantidade
de calor rejeitado
para a fonte
fria num ciclo
![]() Q2
= 2,8.103
J
Q2
= 2,8.103
J
![]()
b)
Cálculo do trabalho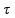 realizado em cada ciclo
realizado em cada ciclo
![]()
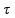 =
Q1
– Q2
=
4,0.103
– 2,8.103
=
Q1
– Q2
=
4,0.103
– 2,8.103
![]()
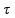 =
1,2.103
J
=
1,2.103
J
Como
são 3000 ciclos o trabalho total será
![]()
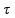 total
=
1,2.103x3000
total
=
1,2.103x3000
![]()
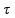 total
=
3,6.106
J.
total
=
3,6.106
J.

05-
a)

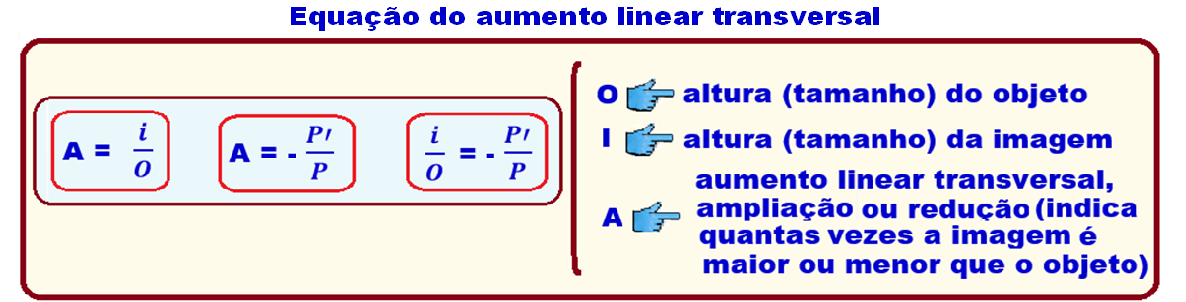
Na figura 1 a calota esférica está se comportando como um espelho esférico côncavo:
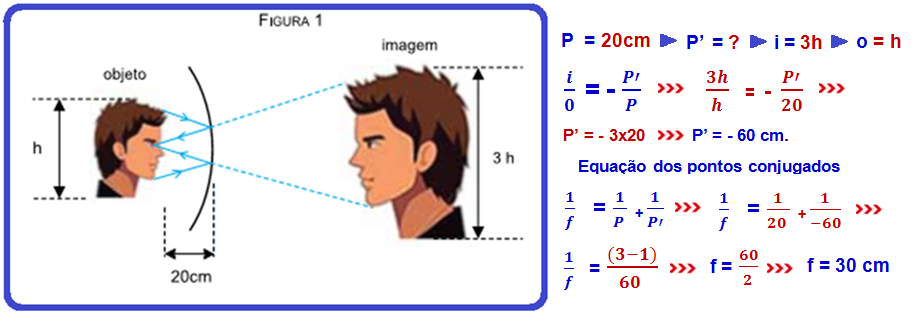
Módulo do espelho côncavo = módulo do espelho convexo = f = 30 cm.
b) Na figura 2 a calota esférica se comporta como um espelho esférico convexo de distância focal
f = - 30 cm (espelhos convexos possuem f < 0)

06-
a)
Cálculo da intensidade
de corrente elétrica i utilizando
os valores
nominais fornecidos:
P
= 25 W e
U
= 40 V
![]() P = i.U
P = i.U
![]() 25 = i.40
25 = i.40
![]() i =
i =
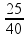 =
0,625 A.
=
0,625 A.
A
carga
elétrica ∆Q no
intervalo de tempo ∆t
= 20
minx60 =
1200 s pode
ser determinada por i
=
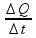
![]()
 0,625
=
0,625
=
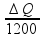
![]()
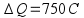 .
.
b)
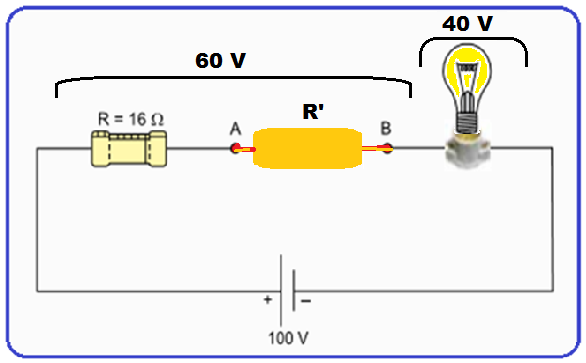
O resistor equivalente R’ (dos n resistores associados em paralelo) está ligado em série ao resistor de 16 Ω e, esse conjunto (16 Ω + R’) deve estar sob ddp de 60 V, pois a lâmpada tem ddp de 40 V e ddp total é de 100 V (veja figura ao lado).
Aplicando
a lei
de Ohm ao conjunto que
está sob
ddp de 60 V
![]() R
=
R
=
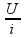
![]() (R’
+ 16) =
(R’
+ 16) =
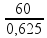
![]()
R’
+ 16 = 96
![]() R’
= 80 Ω.
R’
= 80 Ω.
Então,
você deve
associar em paralelo n resistores de 320Ω de maneira a obter um
único resistor de 80 Ω
![]() n =
n =
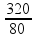
![]() n
= 4.
n
= 4.