UNIFESP-2016

A Universidade Federal de São Paulo (UNIFESP) é uma instituição pública brasileira de ensino superior localizada no estado de São Paulo, sendo importante centro de graduação e pós-graduação no país, baseada no “tripé” Pesquisa-Ensino-Extensão.

É reconhecida pelo Ministério da Educação (MEC) como uma das melhores instituições de ensino superior do país dentre aquelas avaliadas.

No Estado de São Paulo, a Unifesp foi a única instituição que conquistou a nota máxima, 05, e desempenho contínuo de 440 pontos, no ranking das universidades federais. Este é o terceiro ano em que o índice avalia a qualidade das instituições de ensino superior público federal e privado do país. O resultado é composto por avaliações dos cursos de graduações e de pós-graduações das instituições.

O ingresso acontece por seleção pública (vestibular), através de dois sistemas: o SiSU (Sistema de Seleção Unificado do INEP/MEC para as universidades federais de todo o país) e o Sistema Misto. A imensa maioria dos cursos de graduação da UNIFESP utiliza o SiSU para a seleção de novos alunos. O SiSU é adotado por uma ampla maioria de cursos da UNIFESP e utiliza exclusivamente a nota do ENEM do ano corrente para classificar os candidatos.

Todos os candidatos aos cursos que fazem a seleção pelo Sistema Misto fazem as provas do ENEM e também as provas de conhecimentos específicos  promovidas pela própria Universidade; as notas obtidas em todas estas provas serão conjugadas para determinação da nota final de cada candidato e sua consequente classificação.

01-(UNIFESP-SP-016)

Dois veículos, A e B, partem simultaneamente de uma mesma posição e movem-se no mesmo sentido ao longo de uma rodovia plana e retilínea durante 120 s. As curvas do gráfico representam, nesse intervalo de tempo, como variam suas velocidades escalares em função do tempo.

Calcule:

a) o módulo das velocidades escalares médias de A e de B, em m/s, durante os 120 s.

b) a distância entre os veículos, em metros, no instante t = 60 s.

02-(UNIFESP-SP-016)

Um garoto de 40 kg está sentado, em repouso, dentro de uma caixa de papelão de massa desprezível, no alto de uma rampa de 10 m de comprimento, conforme a figura.

a) o módulo da força de atrito, em N, entre a caixa e a rampa no ponto B.

b) a distância percorrida pelo garoto, em metros, desde o ponto A até o ponto D.

03-(UNIFESP-SP-016)

Considere um copo de vidro de 100 g contendo 200 g de água líquida, ambos inicialmente em equilíbrio térmico a 20 ºC.

O copo e a água líquida foram aquecidos até o equilíbrio térmico a 50 ºC, em um ambiente fechado por paredes adiabáticas, com vapor de água inicialmente a 120 ºC.

A tabela apresenta valores de calores específicos e latentes das substâncias envolvidas nesse processo.

Considerando os dados da tabela, que todo o calor perdido pelo vapor tenha sido absorvido pelo copo com água líquida e que o processo tenha ocorrido ao nível do mar, calcule:

a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

04-(UNIFESP-SP-016)

Na entrada de uma loja de conveniência de um posto de combustível, há um espelho convexo utilizado para monitorar a região externa da loja, como representado na figura.

A distância focal desse espelho tem módulo igual a 0,6 m e, na figura, pode-se ver a imagem de dois veículos que estão estacionados paralelamente e em frente à loja, aproximadamente a 3 m de distância do vértice do espelho.

Considerando que esse espelho obedece às condições de nitidez de Gauss, calcule:

a) a distância, em metros, da imagem dos veículos ao espelho.

b) a relação entre o comprimento do diâmetro da imagem do pneu de um dos carros, indicada por d na figura, e o comprimento real do diâmetro desse pneu.

05-(UNIFESP-SP-016)

Um fio metálico homogêneo tem comprimento L e área de secção transversal constante.

Com base no circuito representado na figura 2, calcule:

a) a resistência equivalente, em Ω.

b) a potência total dissipada, em W.

Resolução comentada dos exercícios do vestibular da UNIFESP - 2016

01- a) o módulo das velocidades escalares médias de A e de B, em m/s, durante os 120 s.

Em todo gráfico da velocidade escalar em função do tempo, a área A entre a reta representativa (linha cheia) e o eixo dos tempos é numericamente igual ao deslocamento ∆S efetuado pelo móvel em determinado intervalo de tempo ∆t.

Calculando o deslocamento do móvel A entre t_o = 0 e t = 120 s pela área A_A:

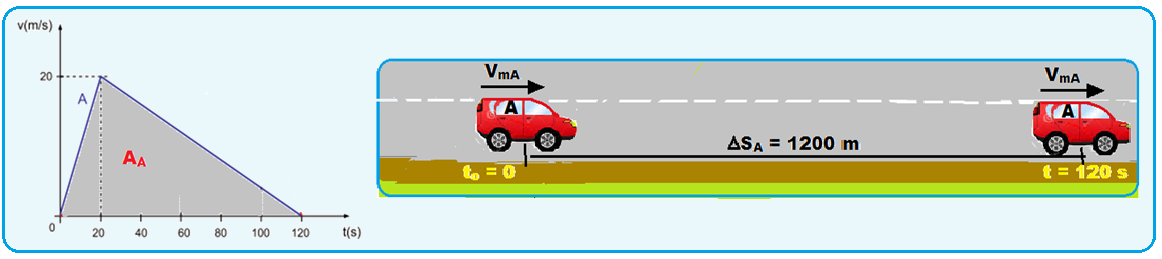
Calculando o deslocamento do móvel B entre t_o = 0 e t = 120 s pela área A_B:

b) a distância entre os veículos, em metros, no instante t = 60 s.

Observe que, no instante t = 60 s eles possuem a mesma velocidade, que é o ponto (P) onde as retas

Acontece que no instante t = 60s, V_B = V_A = V’ = 12 m/s.

Deslocamentos de A e de B entre 0 e 60 s pela área:

02- a) o módulo da força de atrito, em N, entre a caixa e a rampa no ponto B.

Observe na figura a força peso decomposta em suas duas parcelas com as respectivas funções:

Decompondo a força peso, obtemos a expressão matemática de cada uma dessas parcelas:

No caso do exercício, na rampa, a força de atrito pedida tem intensidade F_atAC = µPcosθ = µmgcosθ =

0,25.40.10.0,8 F_atAC = 80 N.

b) a distância percorrida pelo garoto, em metros, desde o ponto A até o ponto D.

Forças que agem sobre o corpo na rampa no trecho AC:

Teorema da energia cinética o trabalho de todas as forças que agem sobre o corpo no trecho total AD é igual à varação da energia cinética entre os pontos A de velocidade V_A = 1m/s e D, de velocidade zero (fornecidos pelo enunciado).

W_FatAC + W_Pp + W_FatCD = E_cD – E_cA - 800 + 2400 - 100d_CD = 0 – mV_A²/2 1600 - 100d_CD = - 40.1²/2 100d_CD = 1620 d_CD = 16,2 m.

É pedido d_AD = 10 + 16,2 d_AD = 26,2 m.

03- a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

Copo Q_c para a temperatura do copo subir de t_o = 20^oC para t = 50^oC, sendo o calor específico do copo c_c = 0,2 cal/g^oC e m_c = 200 g Q_c = m_c.c_c.(t – t_o) = 100.0,2.(50 – 20) Q_c = 600 cal.

Água Q_a para a temperatura da água subir de t_o = 20^oC para t = 50^oC, sendo o calor específico da c_a = 1 cal/g^oC e m_a = 100 g Q_a = m_a.c_a.(t – t_o) = 200.1.(50 – 20) Q_c = 6000 cal.

Quantidade de calor pedida Q_t = 600 + 6000 Q_t = 6600 cal.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

Pelo enunciado a temperatura inicial do vapor de água era t_o = 120 ^oC, que deve se transformar em água líquida a 50 ^oC. Etapas:

1^a Q₁ quantidade de calor cedida pelo vapor de água para passar de t_o = 120^oC para t = 100^oC, sem mudança de estado Q₁ = m_v.c_v.(t – t_o) = m_v.0,5.(100 – 120) Q₁ = - 10m_v.

2ª Q₂ quantidade de calor cedida pelo vapor de água para passar de vapor de água a 100^oC a água líquida a 100^oC (condensação, liquefação) Q₂ = m_v.L = m_V.(-540) Q₂ = - 540m_v.

3^a Q₃ quantidade de calor cedida pela água líquida para passar de t_o = 100^oC para t = 50^oC, sem mudança de estado Q₃ = m_v.c_a.(t – t_o) = m_v.1.(50 – 100) Q₃ = - 50m_v.

Quantidade de calor cedida pelo vapor de água para se transformar em água líquida a 50^oC

Q’ = Q₁ + Q₂ + Q₃ = - 10 m_v – 540m_v – 50m_v Q’ = - 600m_v.

Essa quantidade de calor Q’ cedida pelo vapor de água para ir de 120^oC a água a 50^oC é a mesma recebida pelo sistema (copo + água) para ir de 20^oC a 50^oC (achada no item Q_t = 6600 cal), ou seja, no equilíbrio térmico a soma dessas quantidades de calor trocadas entre o vapor e o copo com água deve ser nula.

- 600m_v + 6600 = 0 m_v = 6600/600 m_v = 11 g.

04- a) a distância, em metros, da imagem dos veículos ao espelho.

Existe uma relação matemática entre a posição (localização) do objeto P, a da imagem P’ e a distância focal f para os espelhos esféricos, denominada equação dos pontos conjugados, no referencial de Gauss, que é fornecida pela expressão:

b) a relação entre o comprimento do diâmetro da imagem do pneu de um dos carros, indicada por d na figura, e o comprimento real do diâmetro desse pneu.

Equação do aumento linear transversal

05- a) a resistência equivalente, em Ω.

Observe a sequência abaixo para o cálculo da resistência equivalente R_eq no circuito da figura 2, onde os três resistores estão em paralelo:

b) a potência total dissipada, em W.

Você pode calcular a potência total dissipada utilizando a resistência equivalente que está submetida à uma tensão de U = 12 V.