Escola naval

01-(Escola Naval - 015/016)

02-(Escola Naval - 015/016)

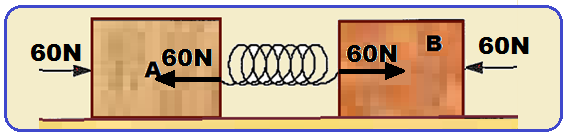
Analise a figura abaixo

Um bloco A de massa 20Kg está ligado a um bloco B de massa 10kg por meio de uma mola.

Os blocos foram empurrados um contra o outro, comprimindo a mola pela ação de duas forças de mesma intensidade F=60N e em seguida colocados sobre a superfície horizontal, conforme indicado na figura acima.

Nessas circunstâncias, os blocos encontram-se em repouso. Sabendo-se que o coeficiente de atrito estático entre os blocos e a superfície é μ_e = 0,4, e que g = 10m/s², é correto afirmar que se as forças F forem retiradas, simultaneamente,

(A) os dois blocos permanecerão em repouso.

(B) o bloco A se deslocará para a esquerda e o bloco B para a direita.

(C) o bloco A se deslocará para a esquerda e o bloco B permanecerá em repouso.

(D) o bloco A permanecerá em repouso e o bloco B se deslocará para a direita.

(E) os dois blocos se deslocarão para a direita.

03-(Escola Naval - 015/016)

Analise a figura abaixo.

No circuito da figura, cada lâmpada incandescente L dissipava 4,00 watts sob uma tensão inicial V, mantida pela bateria de fem e resistência interna desconhecidas.

Quando, então, o filamento de uma das lâmpadas se rompeu (anulando sua corrente), observou-se que a tensão nas lâmpadas aumentou para 5V₀/4.

Considerando as lâmpadas como resis­tências comuns (constantes), a potência total dissipada em watts, nas duas lâmpadas que permaneceram acesas é

04-(Escola Naval - 015/016)

Analise a figura abaixo.

Duas cargas puntiformes desconhecidas (Q₀ , Q₁) estão fixas em pontos distantes, d₀ e d₁, do ponto P, localizado sobre a reta que une as cargas (ver figura).

Supondo que, se um elétron é cuidadosamente colocado em P e liberado do repouso, ele se desloca para direita (no sentido da carga Q₁), sendo assim, pode-se afirmar que, se Q_o e Q_i

(A) são positivas, então d_l < d₀.

(B)são negativas, então d_o < d₁.

(C) têm sinais contrários, Q₁ é a carga negativa.

(D) têm sinais contrários, Q_o é a carga positiva.

(E) têm o mesmo sinal, o campo elétrico resultante em P aponta para a esquerda.

05-(Escola Naval - 015/016)

As turbinas a vapor da propulsão nuclear de um submarino possuem um rendimento de 15% e são

capazes de produzir uma potência mecânica constante de 40 MW nos eixos rotativos.

Se essa potência é entregue em 3,0 minutos, observa-se que a variação de entropia do sistema vapor - turbinas é (1/12) GJ/K.

A temperatura, em °C, do vapor superaquecido produzido pelo reator nuclear vale, aproximadamente

06-(Escola Naval - 015/016)

Analise o gráfico abaixo.

20/31

O trajeto entre duas cidades é de 510km. Considere um veiculo executando esse trajeto.

No gráfico acima, temos a velocidade média do veiculo em três etapas.

Com base nos dados apresentados no gráfico, qual a velocidade média, em km/h, estabelecida pelo veículo no trajeto todo?

07-(Escola Naval - 015/016)

Analise a figura abaixo.

Conforme indica a figura acima, no instante t=0, uma partícula é lançada no ar, e sua posição em função do tempo é descrita pela equação com r em metros e t em segundos.

Após 1,0 segundo, as medidas de sua altura do solo, em metros, e do módulo da sua velocidade, em m/s, serão, respectivamente, iguais a

08-(Escola Naval - 015/016)

Analise a figura abaixo.

Uma casca esférica metálica fina, isolada, de raio R = 4,00 cm e carga Q, produz um potencial elétrico igual a 10,0V no ponto P, distante 156cm da superfície da casca (ver figura).

Suponha agora que o raio da casca esférica foi alterado para um valor quatro vezes menor.

Nessa nova configuração, a ddp entre o centro da casca e o ponto P, em quilovolts, será

09-(Escola Naval - 015/016)

Analise a figura abaixo.

Um instrumento denominado amperímetro de alicate é capaz de medir a corrente elétrica em um ou mais condutores apenas os envolvendo com suas garras (ver figura).

Quando essas são fechadas, o campo magnético produzido pelas correntes envolvidas pode ser medido por um sensor.

Considere que dois condutores retilíneos, muito próximos um do outro, atravessam o centro da área circular, de raio R, entre as garras do medidor.

Sendo assim, o campo magnético medido pelo sensor será

(A) zero, se as correntes nos fios forem de mesmo módulo I e tiverem sentidos contrários.

(B) μ_o.I/πR²_, se as correntes forem de mesmo módulo I e tiverem o mesmo sentido.

(C) μ_o.I/2πR_, se as correntes forem de mesmo módulo I e tiverem o mesmo sentido.

(D) ) μ_o.I/4πR, se as correntes forem de mesmo módulo I e tiverem sentidos contrários.

(E) sempre zero.

10-(Escola Naval - 015/016)

Analise a figura abaixo.

Na figura acima, uma força horizontal, de módulo numericamente igual a dezoito vezes a altura h do seu ponto de aplicação, atua sobre uma viga vertical homogênea presa a uma dobradiça na extremidade inferior.

A viga tem comprimento L = 6,0m e é mantida na posição por um cabo horizontal na extremidade superior. Sabendo que a tração máxima suportada pelo cabo horizontal é de 12N, o valor máximo da componente horizontal da força exercida pela dobradiça sobre a viga é

Resolução comentada dos exercícios da

Escola Naval - 015/016

01-

  O trabalho das forças conservativas, como, por exemplo, as forças peso, da elástica , da elétrica e da magnética não dependem da trajetória, mas apenas das posições inicial e final da mesma.

 Gráficos das energias cinética, potencial gravitacional e mecânica para um corpo demassa m, quando lançado verticalmente para cima, a partir doponto de lançamento, tomado como referencial e desprezando-se as forças resistivas, em função do tempo de subida e descida.

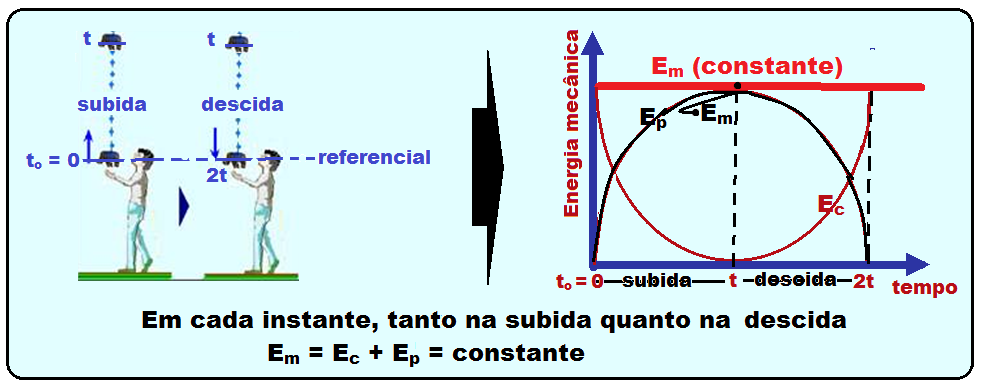
Durante todo o movimento, conclui-se que, à diminuição de energia cinética corresponde um aumento de energia potencial gravitacional e vice-versa, mantendo-se constante a totalidade da energia mecânica.

Observe que as representações gráficas das energias cinética e potencial gravitacional correspondem à duas parábolas invertidas de modo que, em cada ponto, a soma dessas duas energias corresponda à energia mecânica, que é constante. Observe também que o tempo de subida é igual ao tempo de descida, pois as forças dissipativas são desprezadas.

Aplicando a relação trigonométrica temos que:

sen2x = sen x . senx E_c = 4.sen²(2/3t - /2) E_c = 4.sen(2/3t - /2).sen(2/3t -/2)

para t=0 Ec = 4.sen(0 - /2).sen(0 - /2) Ec = 4.(-1).(-1) E_c = 4 J (valor máximo), portanto Ep = 0, pois, pelo princípio da conservação da energia E_m = E_c + E_p = constante.

para t=1,5s Ec = 4.sen( - /2).sen( - /2) Ec = 4.sen(/2).sen(/2) Ec = 4.1.1

Ec = 4 J (valor máximo), portanto Ep = 0, pois, pelo princípio da conservação da energia E_m = E_c + E_p = constante.

para t = 3 s Ec = 4.sen(2 - /2).sen(2 - /2) Ec = 4.sen(2 - /2).sen(2 - /2)

Ec = 4.sen(3/2).sen(3/2) Ec = 4.(-1).(-1) Ec = 4 J (valor máximo), portanto Ep = 0, pois, pelo princípio da conservação da energia E_m = E_c + E_p = constante.

Logo, o único gráfico que corresponde aos valores obtidos é o primeiro.

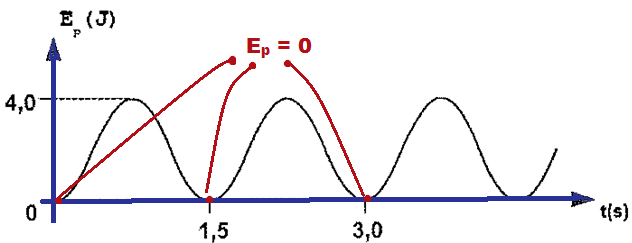
R- A

02- Quando você comprime a mola com forças de intensidade 60N, a extremidade esquerda da mola

estará empurrando o bloco A para a esquerda com F = 60N e a extremidade direita da mola estará empurrando o bloco B para a direita com F = 60N.

Analisando primeiramente o bloco A temos:

Fat A = .N Fat A = .m.g Fat A = 0,4.20.10 Fat A = 80 N

Retirando simultaneamente ambas as forças, o bloco A ficará sujeito a uma força de 60N para a esquerda e uma força de atrito de 80 N para a direita.

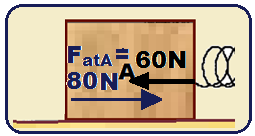
Como a força F vale 60 N e a força de atrito vale 80 N, chegamos a conclusão que o bloco A fica parado, uma vez que o atrito impede seu movimento.

Analisando agora o bloco B:

Fat B = .N Fat B = .m.g Fat B = 0,4.10.10 Fat B = 40 N

Como a força F vale 60 N e a força de atrito vale 40 N, chegamos à conclusão que o bloco B entra em

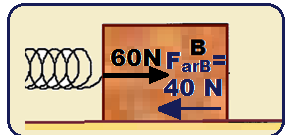
movimento para a direita, uma vez que o atrito agora somente dificulta o movimento do bloco, que acaba sendo impulsionado a sua direita pela ação da mola, sujeito a uma força resultante de F_R = 60 – 40 = 20N..

R- D

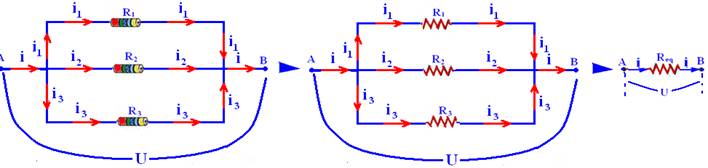
03-

Através da figura verificamos que se trata de uma ligação em paralelo

Associação paralelo, características:

 Os resistores são associados pelos seus terminais, ou seja, todos saem de um mesmo ponto e todos chegam a um mesmo ponto.

 A diferença de potencial (tensão) U de toda a associação (entre A e B) é a mesma para todos os resistores

 A corrente total i é a soma das correntes parciais, ou seja, i = i₁ + i₂ + i₃.

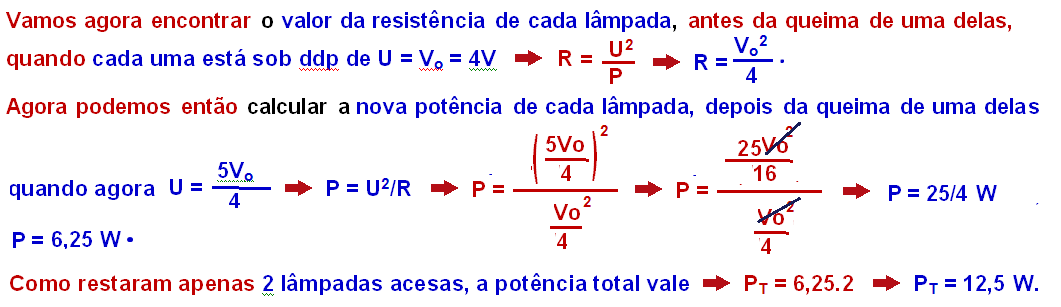
R- C

04- Campo elétrico gerado por uma carga pontual Q

Uma carga puntiforme (Q) geradora de campo provoca num ponto P, distante d da carga, um vetor campo elétrico  que faz surgir sobre uma carga de prova q aí colocada uma força elétrica  de intensidade F=KQq/d², que substituída na equação E=F/q fornece:

 Observe atentamente as figuras abaixo onde a carga geradora Q > 0 provoca em q₁ < 0 localizado em M uma força de atração  e, como q₁ é negativa, campo e força tem mesma direção e sentidos opostos, estando em M se afastando de Q > 0.

Verifique agora que a carga geradora Q > 0 provoca em q₂ > 0 localizado em N uma força de
repulsão  e, como q₂ é positiva, campo e força têm mesma direção e mesmo sentido, estando  em N se afastando de Q > 0.

Generalizando: em qualquer ponto do campo gerado por Q > 0 colocando-se cargas de prova q positivas ou negativas, o campogerado será sempre de afastamento.

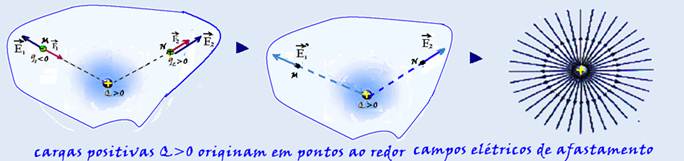
Analogamente, se a carga geradora fosse negativa Q < 0, em todos os pontos o campo elétrico gerado seria de aproximação.

Como o elétron (carga de prova negativa) se desloca para a direita a força sobre ele também é para a direita e o campo elétrico é para a esquerda.

R- E

05- Considere uma determinada máquina realizando certo trabalho. A potência útil (P_u) é a potência que a máquina utiliza na realização de um trabalho externo; a potência dissipada (P_d) corresponde à potência não aproveitada, transformada no interior da máquina em energia térmica (calor).

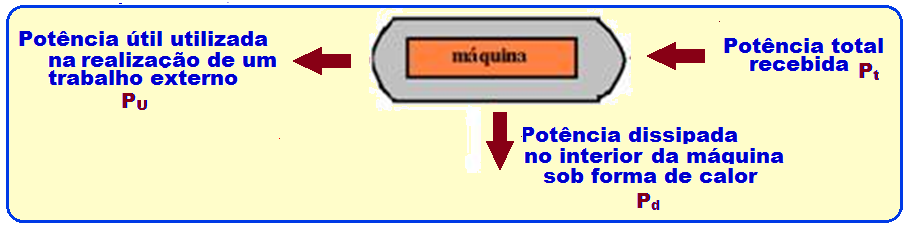
Para poder realizar o trabalho útil (externo), a máquina deve receber uma potência total (P_t), que deve valer: P_t = P_d + P_u.

Portanto, da potência total fornecida à máquina só uma porcentagem, potência útil é aproveitada, pois parte dela é perdida (potência dissipada). Assim, rendimento ( η – letra grega eta) de uma máquina é sua capacidade de realização de determinado trabalho e é  definido como sendo a razão entre a potência útil (P_u) e a potência total (P_t):

Então, por exemplo, se o motor de um carro estiver bem regulado ele apresentará maior rendimento, percorrendo uma distancia maior com a mesma quantidade de combustível que outro carro de mesmas características, mas com o motor desregulado.

Como o rendimento é uma relação entre duas grandezas de mesmas unidades, elas se cancelam e ele não terá unidade (grandeza adimensional).

Sendo P_u sempre menor que P_t,  η  sempre será menor que 1, que normalmente é multiplicado por 100, sendo assim expresso em porcentagem.

Podemos agora calcular a Potência total da turbina:

η  = Pu/P_t 15/100 = 40.10⁶ / P_t P_t = 40.10⁶/15/100 P_t = 4000.10⁶/15 W.

A seguir, encontramos a Energia total consumida em 3 minutos (180s):

E = P_t.t E = (4000.10⁶/15).180 E = 4000. 10⁶.12 E = 48000. 10⁶ J = 48.10⁹ J. Sendo a variação de entropia vapor- turbinas (1/12) GJ/K, conseguimos encontrar a temperatura do vapor por uma regra de três:

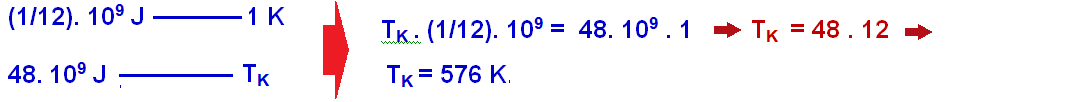Utilizando a relação entre as escala Celsius e Kelvin, temos:

K = C + 273 576 = C + 273 C = 576 – 273 C = 303 ^oC

R- B

06- Em todo gráfico VXt,  a área compreendida entre a reta representativa e o eixo do tempo é numericamente igual ao espaço (ΔS) percorrido pelo móvel.

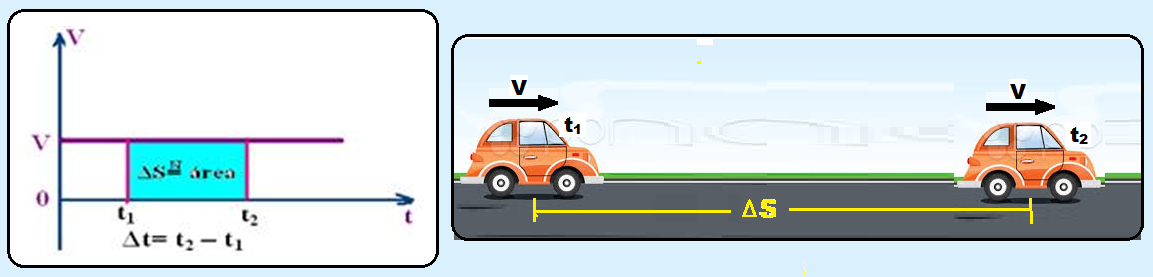
A área do retângulo hachurado acima vale baseXaltura = (t₂ – t₁)XV = Δt.V  área = V.Δt   ΔS=V.Δt   .

Sendo assim, podemos determinar a distância percorrida em cada etapa, calculando cada área :

1ª etapa ΔS₁=b.h = V.Δt  ΔS₁= 55,5.t km

2ª etapa ΔS₂= 0.(t + 2 - t) ΔS₂= 0.2 ΔS₂= 0 km

3ª etapa ΔS₃ = 72.(t + 6 - t - 2) ΔS₃= 72.4 ΔS₃= 288 km

Como o trajeto entre as cidades vale 510 km, podemos encontrar o valor de t ΔS = ΔS₁ + ΔS₂ + ΔS₃ 510 = 55,5t + 0 + 288 510 - 288 = 55,5t t = 222/55,5 t = 4 h.

Logo, o tempo total vale Δt = t + 6 = 4 + 6 Δt = 10 h.

Agora resta apenas determinar a velocidade média:

V_m = ΔS/ Δt Vm = 510/10 Vm = 51 km/h.

R- B

07- Na coordenada cartesiana tridimensional, os elementos i, j e k  são vetores unitários nas direções

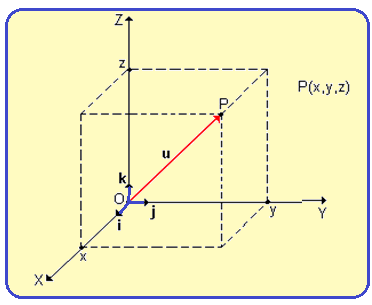
dos eixos x, y e z, respectivamente.

No nosso caso, a coordenada cartesiana é bidimensional e a distância horizontal (eixo x) x é

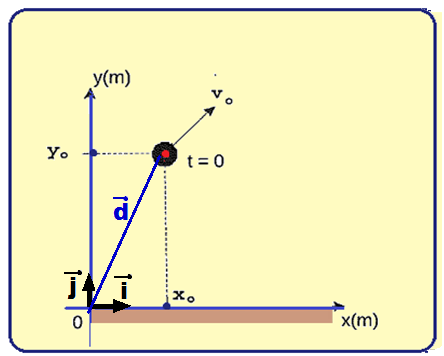
representada pelos valores de i e os do eixo y, pelos valores de j.

Como j representa o eixo y, que corresponde a altura, através da equação podemos determinar a altura no instante t = 1s, usando apenas os valores de j:

r = - 5,0t² + 2,0t + 8,4 y = -5,0.1² + 2,0.1 + 8,4 y = -5 + 2 + 8,4 y = h = 5,4 m.

Na horizontal x, quando t = 1s você terá x = 6,0t + 2,5 = 6.1 + 2,5 x = 8,5 m.

Assim, após 1s, a partícula se deslocou simultaneamente 5,4m para cima e 8,5m para a direita e o módulo de seu deslocamento d foi d² = 5,4² + 8,5² = 29,16 + 72,25 d = √(101,41) = 10,07 = 10m

Velocidade V = d/t = 10/1 V = 10 m/s.

R- E

08- Potencial elétrico de um condutor esférico eletrizado com carga Q

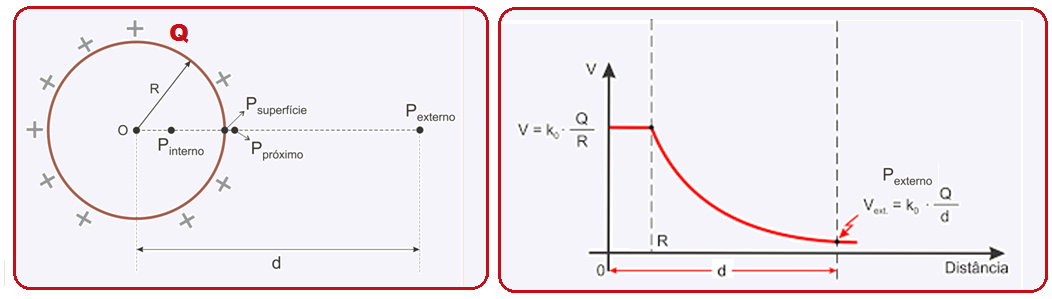
Cálculo do módulo da carga Q utilizando o potencial elétrico fornecido no ponto P, V = 10V, distante d = (0,04+1,56) = 1,6 m do centro da carga V = K.Q/d 10 = k.Q/(0,04 + 1,56) 10 = k.Q/1,6 k.Q = 16

Agora, conseguimos obter o valor do potencial para o raio da esfera 4 vezes menor, no interior da esfera, que é o mesmo que da superfície e de intensidade V_i = k.Q/R V_i = 16/0,01 V_i =

1600 V.

Em seguida, determinamos também o potencial externo V_e = k.Q/d V_e = 16/(0,01+1,56)

V_e = 16/1,57 V_e = 10,2 V

Finalmente, conseguimos obter a ddp entre o centro da casca e o ponto P ddp = V_i – V_e

ddp = 1600 - 10,2 ddp = 1589,8 V ~ 1,59 kV

R- D

09- Um dos processos práticos para se determinar a direção e o sentido do vetor indução magnética  ou vetor campo magnético, é a regra da mão direita.

Esse sentido de depende do sentido da corrente que o origina.

Você coloca o polegar no sentido da corrente com a mão espalmada (primeira figura), em seguida

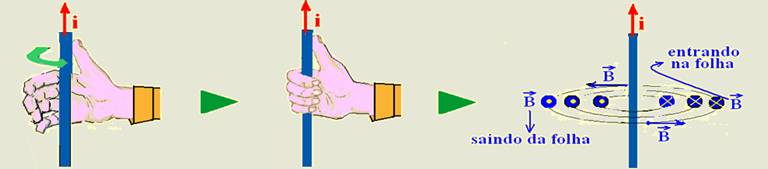
 você fecha a mão para pegar o fio (segunda figura) e o sentido da “fechada” de mão é o sentido do vetor (terceira figura). Observe na terceira figura que  é sempre tangente às linhas de indução em cada ponto.

 Comprova-se experimentalmente que a intensidade do campo magnético depende da intensidade da corrente elétrica i, da distância r do fio até o ponto (P) onde se quer o campo magnético e do meio onde o condutor se encontra.

Essa dependência de com o meio é fornecida pela constante μ que recebe o nome de permeabilidade magnética do meio e no vácuo ela vale  μ_o = 4π.10-7T.m/A. Matematicamente:

Observe na expressão acima que, se as correntes tiverem o mesmo módulo I, os campos magnéticos originados por cada fio terão o mesmo módulo B.

Se você aplicar a regra da mão direita para cada fio, com as correntes tendo sentidos contrários,

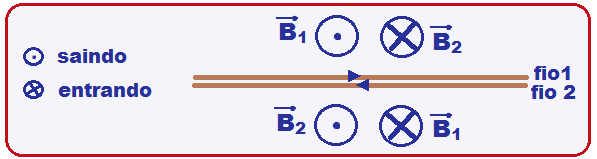
observará que, nas regiões superiores e inferiores, os campos magnéticos criados por cada fio se anulam (sentidos opostos, entrando e saindo da folha) e de mesmo módulo.

Sendo assim, o campo magnético medido pelo sensor do alicate amperímetro será ZERO.

R- A

10- O sinal do momento da força pode ser negativo ou positivo e, por convenção, vamos adotar o sentido horário de rotação em torno de O como positivo e anti-horário como negativo

Condições de equilíbrio de um corpo extenso

São duas as condições para que um corpo extenso rígido esteja em equilíbrio:

1^a – Equilíbrio de translação  ---  A resultante do sistema de forças deve ser nula

2^a – Equilíbrio de rotação  ---  A soma algébrica dos momentos das forças que agem sobre o sistema, em relação à qualquer ponto (pólo O),deve ser nula.

Resolvendo o sistema composto pelas duas equações acima você chega à resolução do exercício.

No caso do nosso exercício, colocando o pólo (eixo de rotação) na dobradiça, em 0, estabelecendo o sentido horário de rotação como positivo e aplicando a 2ª condição (equilíbrio de rotação), temos:

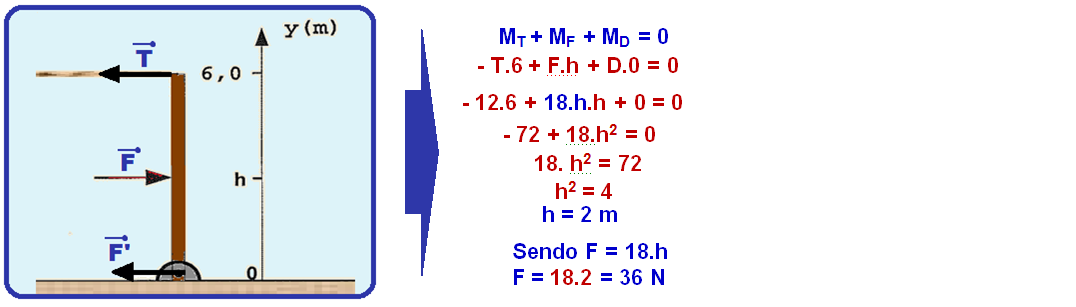
Agora, aplicando a 1ª condição (equilíbrio de translação), temos:

T + D = F

12 + D = 36

D = 36 - 12

D = 24 N

R - C