
UFRGS-2015

A Universidade Federal do Rio Grande do Sul (UFRGS) é uma instituição de ensino superior pública brasileira, mantida pelo Governo Federal do Brasil. Está situada em Porto Alegre, capital do Rio Grande do Sul.
A UFRGS mantém centros de graduação e pós-graduação nas áreas de educação
,letras, engenharias, ciências exatas e ciências humanas. A UFRGS é inovadora na criação de cursos de pós-graduação em nível de especialização e mestrado profissional (MBA) no âmbito das universidades públicas brasileiras.
A UFRGS está na lista das melhores instituições educacionais de ensino superior do mundo, elaborada pela Shanghai Jiao Tong University, onde foram analisadas 12 mil instituições em todo o mundo.
Em outro ranking, organizado pelo Ministério da Educação da Espanha, a Universidade Federal do Rio Grande do Sul aparece em 152° lugar, entre 17 mil instituições pesquisadas. O índice leva em conta a qualidade das pesquisas acadêmicas e o prestígio em âmbito internacional. Na mesma lista a UFRGS aparece na 3ª posição entre as melhores da América Latina.
O Hospital de Clínicas de Porto Alegre (HCPA) faz parte da rede de hospitais universitários do Ministério da Educação e é vinculado academicamente à Universidade Federal do Rio Grande do Sul (UFRGS). O Hospital é referência em todo Brasil e está localizado no centro de Porto Alegre.

01-(UFRGS-RS-015)

Em 2014, comemoraram-se os 50 anos do início da operação de trens de alta velocidade no Japão, os chamados trens-bala.
Considere que um desses trens desloca-se com uma velocidade constante de 360 km/h sobre
trilhos horizontais. Em um trilho paralelo, outro trem desloca-se também com velocidade constante

de 360 km/h, porém em sentido contrário.
Nesse caso, o módulo da velocidade relativa dos trens, em m/s, é igual a
![]()
02-(UFRGS-RS-015)

Trens MAGLEV, que têm como princípio de funcionamento a suspensão eletromagnética,

entrarão em operação comercial no Japão, nos próximos anos. Eles podem atingir velocidades superiores a 550 km/h. Considere que um trem, partindo do repouso e movendo-se sobre um trilho retilíneo, é uniformemente acelerado durante 2,5 minutos até atingir 540 km/h.
Nessas condições, a aceleração do trem, em m/s2, é
![]()
03-(UFRGS-RS-015)

Em uma região onde a aceleração da gravidade tem módulo constante, um projétil é disparado a partir do solo, em uma direção que faz um ângulo α com a direção horizontal, conforme representado na figura abaixo.

Assinale a opção que, desconsiderando a resistência do ar, indica os gráficos que melhor
representam, respectivamente, o comportamento da componente horizontal e o da componente
vertical, da velocidade do projétil, em função do tempo.

![]()
04-(UFRGS-RS-015)

A elipse, na figura abaixo, representa a órbita de um planeta em torno de uma estrela S. Os
pontos ao longo da elipse representam posições sucessivas do planeta, separadas por intervalos de tempo iguais. As regiões alternadamente coloridas representam as áreas varridas pelo raio da trajetória nesses intervalos de tempo. Na figura, em que as dimensões dos astros e o tamanho da órbita não estão em escala, o segmento de reta SH representa o raio focal do ponto H, de comprimento p .

Considerando que a única força atuante no sistema estrela-planeta seja a força gravitacional, são feitas as seguintes afirmações.
I - As áreas S1 e S2, varridas pelo raio da trajetória, são iguais.
II - O período da órbita é proporcional a p3 .
III- As velocidades tangenciais do planeta nos pontos A e H, VA e VH, são tais que VA > VH.
Quais estão corretas?
(A) Apenas I.
(B) Apenas I e II.
(C) Apenas I e III.
(D) Apenas II e III.
(E) I, II e III.
05-(UFRGS-RS-015)

Um carrinho de massa 1 kg move-se retilineamente com velocidade de módulo constante igual a 3 m/s, sobre uma superfície horizontal sem atrito.
A partir de dado instante, o carrinho recebe o impulso de uma força externa aplicada na mesma direção e sentido de seu movimento. A intensidade dessa força, em função do tempo, é dada pelo gráfico abaixo.

A partir desse gráfico, pode-se afirmar que o módulo da velocidade do bloco após o impulso recebido é, em m/s, de
![]()
06-(UFRGS-RS-015)

Dois blocos, 1 e 2, são arranjados de duas maneiras distintas e empurrados sobre uma superfície sem atrito, por uma mesma força horizontal F. As situações estão representadas nas figuras I e II abaixo.

Considerando que a massa do bloco 1 é m1 e que a massa do bloco 2 é m2 = 3 m1, a opção que indica corretamente a intensidade da força que atua entre os blocos, nas situações I e II, é, respectivamente,
![]()
Instrução: As questões 07 e 08 referem-se ao enunciado abaixo.
Na figura abaixo, estão representados dois pêndulos simples, X e Y, de massas iguais a 100 g.

Os pêndulos, cujas hastes têm massas desprezíveis, encontram-se no campo gravitacional terrestre. O pêndulo Y encontra-se em repouso quando o pêndulo X é liberado de uma altura h = 0,2 m em relação a ele.
Considere o módulo da aceleração da gravidade g = 10 m/s2.
07-(UFRGS-RS-015)

Após a colisão, X e Y passam a mover-se juntos, formando um único pêndulo de massa 200 g. Se v é a velocidade do pêndulo X no instante da colisão, o módulo da velocidade do pêndulo de massa 200 g, imediatamente após a colisão, é
![]()
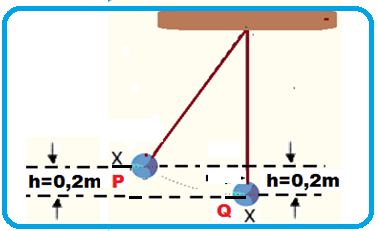
08-(UFRGS-RS-015)

Qual foi o trabalho realizado pelo campo gravitacional sobre o pêndulo X, desde que foi
liberado até o instante da colisão?
![]()
09-(UFRGS-RS-015)

Observe o sistema formado por um bloco de massa m comprimindo uma mola de constante k, representado na figura abaixo.

Considere a mola como sem massa e o coeficiente de atrito cinético entre o bloco e a superfície igual a μc .
Qual deve ser a compressão X da mola para que o bloco deslize sem rolar sobre a superfície horizontal e pare no ponto distante 4X da posição de equilíbrio da mola?
![]()
10-(UFRGS-RS-015)

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.
Dois objetos, R e S, cujos volumes são iguais, são feitos do mesmo material.

R tem a forma cúbica e S a forma esférica. Se R é maciço e S é oco, seus respectivos pesos PR e PS são tais que ......... .
Quando mantidos totalmente submersos em água, a força de empuxo ER exercida sobre R é ........ força de empuxo ES exercida sobre S.
(A) PR > PS – maior do que a
(B) P R > PS – igual à
(C) P R > PS – menor do que a
(D) P R = PS – maior do que a
(E) P R = PS – igual à
RL
11-(UFRGS-RS-015)

A figura abaixo apresenta um diagrama Pressão x Volume. Nele, os pontos M, N e R representam três estados de uma mesma amostra de gás ideal.

Assinale a alternativa que indica corretamente a relação entre as temperaturas absolutas TM, TN e TR dos respectivos estados M, N e R.
![]()
12-(UFRGS-RS-015)

Em uma aula de Física, foram utilizadas duas esferas metálicas idênticas, X e Y: X está suspensa por um fio isolante na forma de um pêndulo e Y fixa sobre um suporte isolante, conforme representado na figura abaixo.

As esferas encontram-se inicialmente afastadas, estando X positivamente carregada e Y eletricamente neutra.
Considere a descrição, abaixo, de dois procedimentos simples para demonstrar possíveis processos de eletrização e, em seguida, assinale a alternativa que preenche corretamente as lacunas dos enunciados, na ordem em que aparecem.
I - A esfera Y é aproximada de X, sem que elas se toquem. Nesse caso, verifica-se experimentalmente que a esfera X é ........ pela esfera Y.
II - A esfera Y é aproximada de X, sem que elas se toquem. Enquanto mantida nessa posição, faz-se uma ligação da esfera Y com a terra, usando um fio condutor.
Ainda nessa posição próxima de X, interrompe-se o contato de Y com a terra e, então, afasta-se novamente Y de X.
Nesse caso, a esfera Y fica ........ .
(A) atraída – eletricamente neutra
(B) atraída – positivamente carregada
(C) atraída – negativamente carregada
(D) repelida – positivamente carregada
(E) repelida – negativamente carregada
13-(UFRGS-RS-015)

No circuito esquematizado abaixo, R1 e R2 são resistores com a mesma resistividade ρ.

R1 tem comprimento 2L e seção transversal A, e R2 tem comprimento L e seção transversal 2A.
Nessa situação, a corrente elétrica que percorre o circuito é
(A) 2AV/(5 ρ L). (B) 2AV/(3 ρ L). (C) AV/( ρ L). (D) 3AV/(2ρ L). (E) 5AV/(2 ρ L).
14-(UFRGS-RS-015)

Partículas α, β e γ são emitidas por uma fonte radioativa e penetram em uma região do espaço onde existe um campo magnético uniforme. As trajetórias são coplanares com o plano desta página e estão representadas na figura que segue.

Assinale a alternativa que preenche corretamente a lacuna do enunciado abaixo.
A julgar pelas trajetórias representadas na figura acima, o campo magnético ........ plano da figura.
(A) aponta no sentido positivo do eixo X, no
(B) aponta no sentido negativo do eixo X, no
(C) aponta no sentido positivo do eixo Y, no
(D) entra perpendicularmente no
(E) sai perpendicularmente do
15-(UFRGS-RS-015)

Na figura abaixo, um raio luminoso i, propagando-se no ar, incide radialmente sobre uma placa semicircular de vidro.

Assinale a alternativa que melhor representa a trajetória dos raios r1 e r2 refratados,
respectivamente, no vidro e no ar.

RL
16-(UFRGS-RS-015)

Um campo magnético uniforme B atravessa perpendicularmente o plano do circuito representado abaixo, direcionado para fora desta página.

O fluxo desse campo através do circuito aumenta à taxa de 1 Wb/s.
Nessa situação, a leitura do amperímetro A apresenta, em ampères,
![]()
(Lei
de Faraday
![]() módulo da variação de fluxo = força eletromotriz/intervalo de
tempo
módulo da variação de fluxo = força eletromotriz/intervalo de
tempo
![]() ΙФI = E/∆t
ΙФI = E/∆t
![]() 1Wb/s = E/1s
1Wb/s = E/1s
![]() E
= 1 V.
E
= 1 V.
17-(UFRGS-RS-015)

Na figura abaixo, estão representadas duas ondas transversais P e Q, em um dado instante de tempo.

Considere que as velocidades de propagação das ondas são iguais.
Sobre essa representação das ondas P e Q, são feitas as seguintes afirmações.
I - A onda P tem o dobro da amplitude da onda Q.
II - A onda P tem o dobro do comprimento de onda da onda Q.
III- A onda P tem o dobro da frequência da onda Q.
Quais estão corretas?
(A) Apenas I.
(B) Apenas II.
(C) Apenas III.
(D) Apenas I e II.
(E) I, II e III.
18-(UFRGS-RS-015)

Assinale a alternativa que preenche corretamente as lacunas do enunciado abaixo, na ordem em que aparecem.
A incidência de radiação eletromagnética sobre uma superfície metálica pode arrancar elétrons dessa superfície.
O fenômeno é conhecido como ........ e só pode ser explicado satisfatoriamente invocando a natureza ........ da luz.
(A) efeito fotoelétrico – ondulatória
(B) efeito Coulomb – corpuscular
(C) efeito Joule – corpuscular
(D) efeito fotoelétrico – corpuscular
(E) efeito Coulomb – ondulatória
19-(UFRGS-RS-015)

O físico francês Louis de Broglie (1892-1987), em analogia ao comportamento dual onda-partícula
da luz, atribuiu propriedades ondulatórias à matéria.
Sendo a constante de Planck h = 6,6.10-34 J.s, o comprimento de onda de Broglie para um elétron
(massa m = 9.10-31 kg) com velocidade de módulo v = 2,2.106 m/s é, aproximadamente,
![]()
RESOLUÇÕES
01- 1° caso: se os dois móveis estiverem andando no mesmo sentido, o valor da velocidade relativa é dado pelo módulo da diferença entre os módulos das duas velocidades escalares. Dessa forma, temos:
|vrel |= |vA |- |vB |
2° caso: se os dois móveis estiverem andando em sentidos contrários, o valor absoluto da velocidade relativa é dado pela soma dos módulos das duas velocidades escalares. Assim, temos:
|vrel |= |vA |+ |vB |
No
caso do exercício eles se movem em sentidos contrários
![]() |vrel |=
|vA |+
|vB |
= |360 |+
|360 |
|vrel |=
|vA |+
|vB |
= |360 |+
|360 |![]()
|vrel | = 720 km/h/3,6 = 200 m/s.
R- C
02-
Vo
= 0
![]() V = 540/3,6 = 150m/s
V = 540/3,6 = 150m/s
![]() ∆t = 2,5minx60 = 150s
∆t = 2,5minx60 = 150s
![]() a = ∆V/∆t = (150
– 0)/150
a = ∆V/∆t = (150
– 0)/150
![]() a = 1m/s2.
a = 1m/s2.
R- B
03- Trata-se de um lançamento oblíquo onde,na vertical (Y) você tem as funções(equações), com os respectivos gráficos
Equação da posição (dos espaços) ou da altura Y
S=So + Vo.t + a.t2/2 --- Y=Yo + Voy.t – gt2/2 --- Y=0 + Voy.t – gt2/2 --- Y= Voy.t – gt2/2, com Voy=Vo.senα
![]()
Equação da velocidade Vy
V=Vo + a.t --- Vy=Voy – g.t, com Voy=Vo.senα
![]()
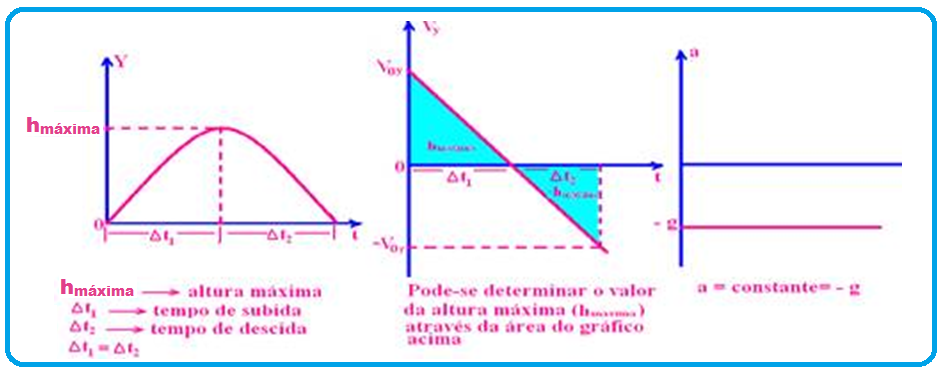
Movimento parcial na direção horizontal (eixo X)
Sendo
o movimento apenas na horizontal, a projeção
do vetor aceleração da gravidade (![]() )
no eixo X
é nula
e, nesse caso o movimento é uniforme (MU) com
velocidade constante Vox,
de
equação
X = Voxt
e cujo gráfico da velocidade Vx
, constante, é uma reta paralela ao eixo dos tempos:
)
no eixo X
é nula
e, nesse caso o movimento é uniforme (MU) com
velocidade constante Vox,
de
equação
X = Voxt
e cujo gráfico da velocidade Vx
, constante, é uma reta paralela ao eixo dos tempos:
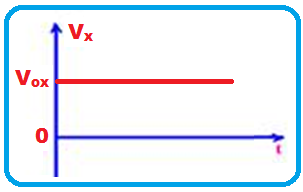
R- B
04-
I.
Correta
![]() Segunda
lei de Kepler (lei das áreas)
Segunda
lei de Kepler (lei das áreas)
“ O segmento de reta imaginário que une o centro do Sol ao centro do planeta descreve áreas
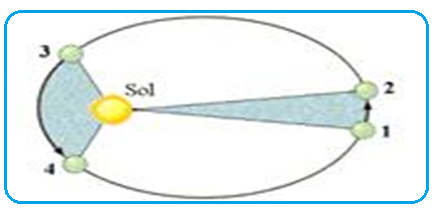
proporcionais aos tempos gastos para percorrê-las”
O enunciado afirma que o planeta percorre esses intervalos de posições em tempos iguais.
II.
Falsa
![]() Terceira
lei de Kepler (lei dos períodos)
Terceira
lei de Kepler (lei dos períodos)
“ Os quadrados dos períodos T de revolução dos planetas (tempo que demora para efetuar uma volta completa em torno do Sol) são proporcionais aos cubos das suas distâncias médias R ao Sol”
T2/R3=constante=K.
No
caso do exercício R=P
![]() T2
= kP3
T2
= kP3
![]() o correto seria: o quadrado
do
período da órbita é proporcional a p3
.
o correto seria: o quadrado
do
período da órbita é proporcional a p3
.
III.
Correta
![]() Pela
lei das áreas: “ O segmento
de reta
imaginário que une o centro do Sol ao centro do planeta descreve
áreas
proporcionais
aos tempos gastos para percorrê-las”
Pela
lei das áreas: “ O segmento
de reta
imaginário que une o centro do Sol ao centro do planeta descreve
áreas
proporcionais
aos tempos gastos para percorrê-las”
Então:
A1/∆t1~A2/∆t2=constante=K

Observe
na expressão
acima
que quando A1=A2
![]() ∆t1= ∆t2, ou
seja, para o arco maior 3,4,
ser percorrido no mesmo
intervalo de tempo
que o arco menor 1,2,
a velocidade
em 3,4
(mais perto do Sol - periélio)
deve ser maior
que a velocidade em 1,2
(mais afastado do Sol – afélio).
∆t1= ∆t2, ou
seja, para o arco maior 3,4,
ser percorrido no mesmo
intervalo de tempo
que o arco menor 1,2,
a velocidade
em 3,4
(mais perto do Sol - periélio)
deve ser maior
que a velocidade em 1,2
(mais afastado do Sol – afélio).
Portanto os planetas aceleram do afélio para o periélio e retardam do periélio para o afélio.
R- C
05-
Em
todo gráfico Fxt
o
impulso
recebido pela aplicação da força é numericamente
igual à área sob a
curva
![]()
![]() I
= área = (B + b).h/2
= (2 + 1).4/2 = 12/2
I
= área = (B + b).h/2
= (2 + 1).4/2 = 12/2
![]() I
= 6 N.s.
I
= 6 N.s.
O
teorema
do impulso
afirma que o impulso
é igual à variação da quantidade de movimento (momentum linear)
![]() I = ∆Q = 6 N.s
I = ∆Q = 6 N.s
![]() ∆Q = m∆V = m
(V – Vo)
∆Q = m∆V = m
(V – Vo)
![]() 6 = 1.(V – 3)
6 = 1.(V – 3)
![]() V =
6 + 3
= 9 m/s.
V =
6 + 3
= 9 m/s.
R- E
06- Colocando as forças que agem sobre cada bloco, na direção do movimento:
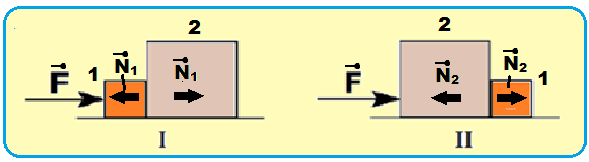
I
![]() bloco 1
bloco 1
![]() FR1
= m1.a1
FR1
= m1.a1
![]() F
– N1
= m1.a1
(I)
F
– N1
= m1.a1
(I)
I
![]() bloco 2
bloco 2
![]() FR
= 3m1.a1
FR
= 3m1.a1
![]() N1
= 3m1.a1
(II)
N1
= 3m1.a1
(II)
(I)
+ (II)
![]() F = 4m1a1
F = 4m1a1
![]() a1
= F/4m1
(III)
a1
= F/4m1
(III)
![]() (III) em (I)
(III) em (I)
![]() N1
= 3m1.(F/4m1)
N1
= 3m1.(F/4m1)
![]() N1
= 3F/4
N1
= 3F/4
II
![]() bloco 1
bloco 1
![]() FR2
= m1.a2
FR2
= m1.a2
![]() N2
= m1.a2
(I)
N2
= m1.a2
(I)
II
![]() bloco 2
bloco 2
![]() FR2
= 3m1.a2
FR2
= 3m1.a2
![]() F – N2
= 3m1.a2
(II)
F – N2
= 3m1.a2
(II)
(I)
+ (II)
![]() F = 4m1a2
F = 4m1a2
![]() a2
= F/4m1
(III)
a2
= F/4m1
(III)
![]() (III) em (I)
(III) em (I)
![]() N2
= m1.(F/4m1)
N2
= m1.(F/4m1)
![]() N2
= F/4
N2
= F/4
R- D
07- Cálculo da velocidade com que o pêndulo X (partindo de P) atinge o pêndulo Y (em Q), imediatamente antes da colisão, pelo teorema da conservação da energia mecânica:
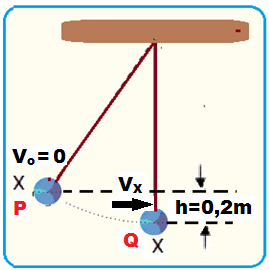
EmXP
= mVX2/2
+ mgh =
0,1.02/2
+ 0,1.10.0,2
=
0 + 0,2
![]() EmXP
= 0,2 J.
EmXP
= 0,2 J.
EmXQ
= mVY2/2
+ mgh =
0,1.VY2/2
+ 0,1.10.0
=
50VY2
+ 0
![]() EmXQ
= 0,05VY2.
EmXQ
= 0,05VY2.
EmX
= EmY
![]() 0,2 = 0,05VY2
0,2 = 0,05VY2
![]() VXQ
= V = 2 m/s.
VXQ
= V = 2 m/s.
Utilizando a conservação da quantidade de movimento antes e depois da colisão:
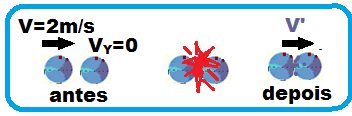
Qsa
= mXV
+ MYVY
= 100.2
+ 100.0
![]() Qsa
= 200 kgm/s.
Qsa
= 200 kgm/s.
Qsd
= mXV
+ MYVY
= 100.V’
+ 100.V’
![]() Qsa
= 200V’.
Qsa
= 200V’.
Qsa
= Qsd
![]() 200 = 200V’
200 = 200V’
![]() V’ = 1m/s = V/2.
V’ = 1m/s = V/2.
R- E
08-
Trabalho
como variação de energia potencial gravitacional
![]() WP
=mgh
= 0,1.10.0,2 =
0,2 J.
WP
=mgh
= 0,1.10.0,2 =
0,2 J.
R- B
09-
Energia
mecânica do bloco no ponto
P
= energia potencial elástica armazenada
pela mola quando ela está comprimida
de x no ponto
P
![]() EmP
=Epe
= kx2/2.
EmP
=Epe
= kx2/2.
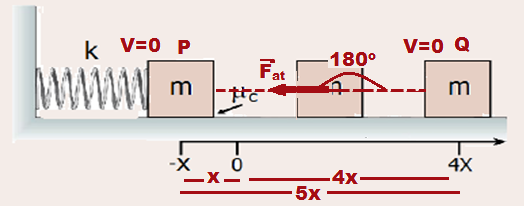
Energia
mecânica do bloco no ponto
Q, onde
está em repouso
![]() EmQ
= 0.
EmQ
= 0.
Toda
essa energia
dissipada
entre os pontos
P e Q (∆Em)
corresponde ao trabalho
da força de atrito
(Wfat)
nesse percurso de d=
5x
![]() ∆Em
= Wfat
∆Em
= Wfat
![]() (0 - kx2/2)
= Fat.d.cosα
(0 - kx2/2)
= Fat.d.cosα
![]() - kx2/2
=μPdcos180o
- kx2/2
=μPdcos180o
![]()
-
kx2/2
= μmg5x(-1)
![]() kx2/2
= 5μmgx
kx2/2
= 5μmgx
![]() x
= 10μmg/k.
x
= 10μmg/k.
R- E
10-
Quanto
ao peso
![]() como são feitos de mesmo
material e R é maciço e S oco,
a massa
de R
é maior
que a massa de S e, sendo P = mg (com g constante), PR
> PS.
como são feitos de mesmo
material e R é maciço e S oco,
a massa
de R
é maior
que a massa de S e, sendo P = mg (com g constante), PR
> PS.
Quanto
ao empuxo
que é fornecido por E
= dágua.Vágua
deslocada.g
![]() dágua
é
a mesma,
como eles possuem o mesmo
volume
(independente do formato) o Vágua
deslocada
é o mesmo
e a aceleração
da gravidade g é a mesma. Portanto ER
= ES.
dágua
é
a mesma,
como eles possuem o mesmo
volume
(independente do formato) o Vágua
deslocada
é o mesmo
e a aceleração
da gravidade g é a mesma. Portanto ER
= ES.
R- B
11- Aplicando a equação geral dos gases perfeitos simultaneamente aos três estados:
PMVM/TM
= PNVN/TN
= PRVR/TR
![]() 6.105.0,1/TM
= 4.105.0,2/TN
= 2.105.0,3/TR
6.105.0,1/TM
= 4.105.0,2/TN
= 2.105.0,3/TR
![]() 0,6/TM
= 0,8/TN
= 0,6/TR
0,6/TM
= 0,8/TN
= 0,6/TR
![]()
TM/3
= TR/3
= TN/4
![]() TM
= TR
< TN.
TM
= TR
< TN.
R- E
12-
Situação
I
![]() X
está eletrizada com carga positiva e Y, neutra.
Quando são aproximadas, X
e Y são atraídas
por
indução eletrostática.
X
está eletrizada com carga positiva e Y, neutra.
Quando são aproximadas, X
e Y são atraídas
por
indução eletrostática.
Se você não domina a teoria, ela está a seguir:
Aproxima-se um condutor eletrizado, por exemplo, negativamente de um condutor neutro, sem encostar, mas bem próximos (figura 1).
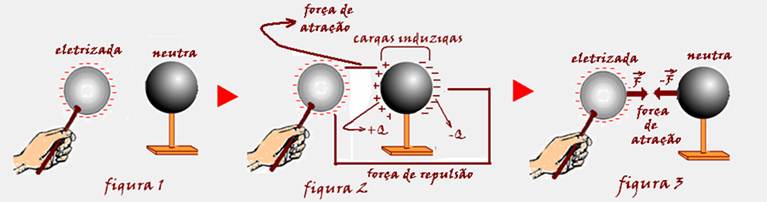
Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2). Observe na figura 2 que a força de atração entre as cargas negativas e positivas é maior que aforça de repulsão entre as cargas negativas porque a distância entre as cargas que se atraem é menor e, quanto menor a distância entre cargas de mesmo módulo, maior a força entre elas.
Portanto, um corpo eletrizado pode atrair um corpo neutro, figura 3.
Situação
II
![]() Trata-se de eletrização
por indução. Veja teoria abaixo:
Trata-se de eletrização
por indução. Veja teoria abaixo:
Aproxima-se um condutor eletrizado, por exemplo, negativamente. (indutor) de um condutor neutro que se deseja eletrizar (induzido), sem encostar, mas bem próximos (figura 1).
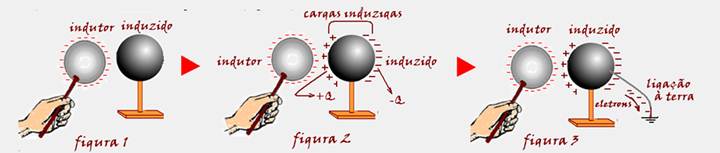
Os elétrons livres do indutor serão repelidos, ficando o lado direito do induzido com excesso de elétrons e o lado esquerdo com falta de elétrons, fenômeno que recebe o nome de indução elétrica (figura 2). As cargas elétricas que se concentram nas duas extremidades opostas (denominadas cargas induzidas) são de mesmo módulo, mas de sinais opostos e, por esse motivo o induzido continua neutro. Em seguida, ainda na presença do indutor você liga o induzido à terra (fio terra ou com seu dedo) e observa que elétrons se deslocam do induzido para a terra (figura 3). Afastando agora o indutor para bem longe, as cargas
elétricas se repelem e espalham pela superfície externa do induzido, que fica eletrizado com cargas de sinal oposto ao do indutor (figura 4)
Se o indutor tivesse cargas positivas, ao final de todo o processo o induzido ficaria eletrizado com cargas negativas.
R- C
13-
Segunda
lei de Ohm
![]() R = ρL/A.
R = ρL/A.
Resistor
1
![]() R1
= ρ2L/A
R1
= ρ2L/A
![]() resistor 2 R2
= ρL/2A.
resistor 2 R2
= ρL/2A.
Resistor equivalente Req = R1 + R2 = ρ2L/A + ρL/2A = 5ρL/2A.
Req = V/i i = V/Req = V/5ρL/2A i = 2AV/5ρL.
R- A
14-
Radiação
alfa (α):
também chamada de partículas
alfa ou raios alfa,
são partículas carregadas por dois prótons e dois nêutrons,
sendo, portanto, núcleos
de hélio.
Apresentam carga
positiva
+2 e número de massa 4.
Radiação
beta (β):
raios
beta ou partículas beta,
são elétrons,
partículas negativas
com carga – 1 e número de massa 0.
Radiação
Gama (γ):
ou raios gama.
O comprimento de onda desta radiação varia de 0,5![]() a 0,00
a 0,00![]() (unidade de medida: angstron). As radiações
gama são ondas eletromagnéticas,
e possuem carga
e massa
nulas,
emitem continuamente calor e têm a capacidade de ionizar o ar e
torná-lo condutor de corrente elétrica
(unidade de medida: angstron). As radiações
gama são ondas eletromagnéticas,
e possuem carga
e massa
nulas,
emitem continuamente calor e têm a capacidade de ionizar o ar e
torná-lo condutor de corrente elétrica
Quando as partículas penetram no campo magnético, todas tem velocidade vertical e para cima --- o campo magnético B penetra no papel --- pela regra da mão esquerda a força que age sobre a carga positiva é horizontal e para a esquerda (é a α) --- portanto a carga positiva é desviada para a
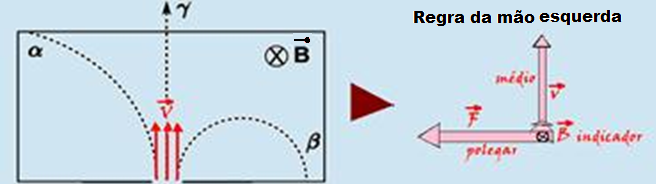
esquerda --- na carga negativa o sentido dessa força é invertido --- ela sofre desvio para a direita (é a β) --- a neutra não sofre desvio --- a neutra não sofre desvio (é a γ) --- observe que o desvio da α é menor, ou seja, ela possui maior inércia e consequentemente maior quantidade de movimento e maior massa.
R- D
15-
Caso
particular da refração da luz
![]() todo raio de luz que incide perpendicularmente
(radialmente)
sobre a superfície
de separação
de dois meios homogêneos e transparentes (no caso, ar-vidro) não
sofre desvio e passa pelo ponto O (centro da placa semicircular).
todo raio de luz que incide perpendicularmente
(radialmente)
sobre a superfície
de separação
de dois meios homogêneos e transparentes (no caso, ar-vidro) não
sofre desvio e passa pelo ponto O (centro da placa semicircular).
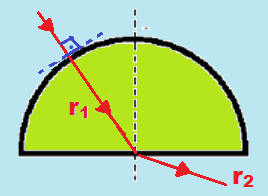
Ao sair para o ar passando de um meio mais refringente para outro menos refringente, o raio de luz aumenta a velocidade se afastando da normal.
R- A
16- Essa força eletromotriz de 1V gerada pela variação de fluxo magnético no interior do circuito provoca uma diminuição de 1V na ddp da bateria, pois se opõe a ela (lei de Lenz), fazendo com que o circuito fique sujeito a uma ddp de U = 3 – 1 = 2V.
R
= U/i
![]() 2 = 2/i
2 = 2/i
![]() i = 1 A.
i = 1 A.
R - C
17- I - incorreta. As ondas P e Q possuem a mesma amplitude AP = AQ (veja figura)
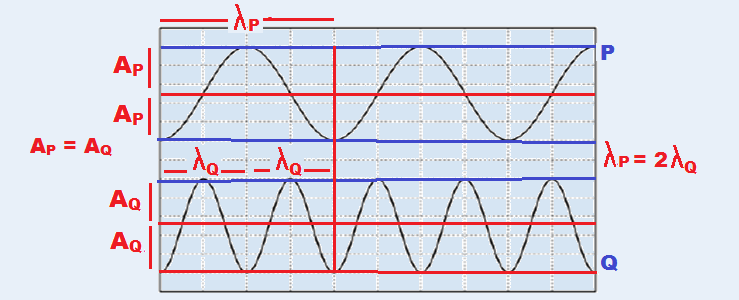
II – correta (veja figura).
III
– incorreta
![]() pelo enunciado as velocidades de propagação são iguais
pelo enunciado as velocidades de propagação são iguais
![]() VP
= VQ
= V
VP
= VQ
= V
![]()
VP
=λP.fP
=
2λQ
λQ
![]() fP
=
V/2λQ
(I)
fP
=
V/2λQ
(I)
![]() VQ
= λQ.fQ
VQ
= λQ.fQ
![]() fQ
= V/λQ
(II).
fQ
= V/λQ
(II).
(I)/(II)
![]() fP/fQ
= V/2λQ
X
λQ/V
fP/fQ
= V/2λQ
X
λQ/V
![]() fQ
= 2fP.
fQ
= 2fP.
R- B
18- Efeito fotoelétrico - Heinrich Rudolf Hertz, em 1887, detectou e gerou em laboratório, em uma

série de experiências que, quando a luz (onda eletromagnética, radiação eletromagnética) de freqüência suficientemente alta incide sobre a superfície de um metal, ela pode retirar elétrons do mesmo. Esse fenômeno ficou conhecido como efeito fotoelétrico.
A luz tem caráter dual: os fenômenos de reflexão, refração, interferência, difração e polarização da luz podem ser explicados pela teoria ondulatória e os de emissão e absorção podem ser explicados pela teoria corpuscular.
R- D
19- O físico francês Louis de Broglie apresentou, em 1924, a seguinte hipótese que, depois, em 1927

foi comprovada experimentalmente: “partículas também possuem propriedades ondulatórias” --- das equações E=m.c2 --- c – velocidade da luz no vácuo --- E=h.f --- c=λf --- f=c/λ --- mc2=hf --- mc2=hc/λ --- λ=h/mc --- mc=Q – quantidade de movimento --- a quantidade de movimento Q=m.v evidencia o caráter corpuscular da luz enquanto que o comprimento de onda λ evidencia seu caráter ondulatório.
As naturezas ondulatória e corpuscular da luz são complementares e não antagônicas
No
caso do exercício
![]() λ=h/mc
λ=h/mc ![]() c=v
c=v
![]() λ = 6,6.10-34/9.10-31.2,2.106
= 3,3.10-10
m.
λ = 6,6.10-34/9.10-31.2,2.106
= 3,3.10-10
m.
R- A