Vestibulares recentes – Física Térmica
Termologia
01- (UECE - Universidade Estadual do Ceará – 2020)
Em hotéis, é comum o aquecimento de água ser a gás ou outro combustível, sendo que para o chuveiro seguem dois canos: um com água natural e outro com água aquecida.
Antes da saída do chuveiro, há um misturador, que homogeneíza a mistura.
Considere que após o misturador, por falhas na qualidade do isolamento térmico dos canos, há passagem de calor para o ambiente antes de a água sair no chuveiro. Considerando esse sistema, é correto afirmar que
A) há transferência de calor da água quente para a fria no misturador e, no trecho entre o misturador e a saída do chuveiro, há somente ganho de energia térmica da mistura.
B) há transferência de calor da água quente para a fria no misturador e, no trecho entre o misturador e a saída do chuveiro, há perda de energia térmica da mistura.
C) não há transferência de calor da água quente para a fria no misturador e, no trecho entre o misturador e a saída do chuveiro, há perda de energia térmica da mistura.
D) não há transferência de calor da água quente para a fria no misturador e, no trecho entre o misturador e a saída do chuveiro, há ganho de energia térmica da mistura.
Há transferência de calor da água quente para a fria no misturador e, se há passagem de calor para o ambiente antes de a água sair no chuveiro, no trecho entre o misturador e a saída do chuveiro, há perda de energia térmica da mistura.
R- B
02- (Faculdade de Tecnologia do Estado de São Paulo – FATEC – 2020)
Recentemente, uma empresa britânica apresentou um protótipo de um motor a jato hipersônico que permitirá às aeronaves comerciais voarem a uma velocidade muito acima da velocidade do som, fazendo com que uma viagem de São Paulo à Austrália dure, aproximadamente, 4 horas (atualmente essa viagem dura cerca de 24 horas).
Isso só é possível devido ao fato de o motor ser alimentado por uma mistura de hidrogênio e
oxigênio. Esse motor “suga” o ar à sua frente fazendo com que os gases, antes de entrarem no combustor, sejam resfriados por um sistema denominado pre-cooler.
Esse dispositivo consegue resfriar os gases variando a temperatura 1 000 K em cerca de 50 ms. Assim, ele aumenta a eficiência de combustível.
Com base nessas informações, podemos afirmar que a taxa de variação de resfriamento térmico, em °C/s, é
(A) 25 460
(B) 20 000
(C) 2 546
(D) 2 000
(E) 250
R- B
03-Universidade Estadual de Maringá (UEM) – PR - 2020
Em relação às radiações térmicas, assinale o que for correto.
01) Todo corpo emite energia na forma de radiações térmicas se sua temperatura (medida na escala Kelvin) não for nula.
02) Quando a superfície de um corpo está na temperatura ambiente, a radiação térmica emitida por ele é predominantemente infravermelha.
04) A quantidade total de energia emitida por unidade de tempo e por unidade de área da superfície externa de um corpo a uma temperatura (medida na escala Kelvin) é diretamente proporcional ao quadrado dessa temperatura.
08) Se a temperatura de um corpo permanece constante ao longo do tempo, então ele não emite nem absorve energia na forma de radiação térmica.
16) Em uma mesma temperatura, as radiações emitidas por qualquer corpo negro são independentes do material de que ele é feito
Para este exercício, é necessário relembrar o conceito de radiação térmica. Pela Lei de Stefan-Boltzmann:
Vamos avaliar cada uma das alternativas:
Todo corpo emite energia na forma de radiações térmicas se sua temperatura (medida na escala Kelvin) não for nula.
De
fato, pela Lei de Stefan-Boltzmann, se
,
.
Quando a superfície de um corpo está na temperatura ambiente, a radiação térmica emitida por ele é predominantemente infravermelha.
De
fato, todo corpo emite energia desde que
.
A radiação térmica está predominantemente na região do
infravermelho, logo esta é invisível ao olho humano,
mas ainda somos capazes de sentir esta radiação na pele em forma de
transferência de calor por radiação.
A quantidade total de energia emitida por unidade de tempo e por unidade de área da superfície externa de um corpo a uma temperatura (medida na escala Kelvin) é diretamente proporcional ao quadrado dessa temperatura.
Esta
alternativa é falsa. Esta
energia por unidade de tempo e por unidade de área é diretamente
proporcional a
.
Se a temperatura de um corpo permanece constante ao longo do tempo, então ele não emite nem absorve energia na forma de radiação térmica.
Pela
Lei de Stefan-Boltzmann, se
então há energia sendo emitida em forma de radiação térmica.
Além disso, a
absorção de energia também não cessa.
Logo, esta
alternativa está incorreta.
Em uma mesma temperatura, as radiações emitidas por qualquer corpo negro são independentes do material de que ele é feito.
Esta
alternativa é verdadeira. No caso de corpos negros (capazes de
absorver toda radiação incidente sobre eles),
,
e, portanto, o que diferencia as radiações é exclusivamente a
temperatura.
Portanto, as alternativas corretas são 01), 02) e 16).
04- (ENEM-MEC-019)
O objetivo de recipientes isolantes térmicos é minimizar as trocas de calor com o ambiente externo.
Essa troca de calor é proporcional à condutividade térmica k e à área interna das faces do recipiente, bem como à diferença de temperatura entre o ambiente externo e o interior do recipiente, além de ser inversamente proporcional à espessura das faces.
A fim de avaliar a qualidade de dois recipientes A (40cm×40cm×40cm) e B (60cm×40cm×40cm), de faces de mesma espessura, uma estudante compara suas condutividades térmicas kA e kB.
Para isso suspende, dentro de cada recipiente, blocos idênticos de gelo a 0 °C, de modo que suas superfícies estejam em contato apenas com o ar. Após um intervalo de tempo, ela abre os recipientes enquanto ambos ainda contêm um pouco de gelo e verifica que a massa de gelo que se fundiu no recipiente B foi o dobro da que se fundiu no recipiente A.
A razão kA/kB é mais próxima de
Lei de Fourier
A constante K é denominada de coeficiente de condutividade térmica é uma característica da natureza do material que separa os dois meios.
R-
B
05- (ENEM-MEC-019)
Em 1962, um jingle (vinheta musical) criado por Heitor Carillo fez tanto sucesso que extrapolou as fronteiras do rádio e chegou à televisão ilustrado por um desenho animado.
Nele, uma pessoa respondia ao fantasma que batia em sua porta, personificando o “frio”, que não o deixaria entrar, pois não abriria a porta e compraria lãs e cobertores para aquecer sua casa.
Apesar de memorável, tal comercial televisivo continha incorreções a respeito de conceitos físicos relativos à calorimetria.
Para solucionar essas incorreções, deve-se associar à porta e aos cobertores, respectivamente, as funções de:
(A) Aquecer a casa e os corpos.
(B) Evitar a entrada do frio na casa e nos corpos.
(C) Minimizar a perda de calor pela casa e pelos corpos.
(D) Diminuir a entrada do frio na casa e aquecer os corpos.
(E) Aquecer a casa e reduzir a perda de calor pelos corpos.
Quem se propaga é o calor e essa propagação ocorre sempre que há diferença de temperatura entre dois ou mais corpos.
Essa propagação ocorre sempre do corpo de maior para o de menor temperatura.
As roupas de lã, os cobertores, os pelos dos animais, o isopor, a serragem são ótimos isolantes
retêm o ar entre suas fibras.
Assim, no caso do exercício, a porta a lã e os cobertores se são isolantes térmicos e podem minimizar a perda de calor pela casa e pelos corpos.
R- C
Calor específico (sensível), calor latente e trocas de calor
06- (Faculdade de Tecnologia Termomecânica – SP- meio do ano – 019/020)
Num recipiente termicamente isolado, água e gelo são misturados, e os dados iniciais são mostrados na tabela.
Considerando que a troca de calor só ocorre entre o gelo e a água, e sendo o calor latente de fusão do gelo igual a 80 cal/g, a temperatura de equilíbrio térmico dessa mistura será
(A) – 2,0 ºC.
(B) 0 ºC.
(C) 2,5 ºC.
(D) 5,0 ºC.
(E) 7,5 ºC.
De
gelo a – 10 oC até água a 0o C 
quantidade
de calor recebido pelo gelo de massa mg = 200g para passar de –
10oC até 0 oC Q1 =
m.c.(t – to) =
200.0,5.(0 – ( -10)) = 100.10 Q1 =
1000 cal.
Fundindo
gelo a 0 oC (de
gelo a 0 oC até água a 0 oC) Q2 =
m.L =
200.80 Q2 =
16000 cal.
De
água a 0 oC até água a te Q3 =
m.c.(te – to) =
200.1.(te – 0) Q3 =
200te.
Quantidade
de calor recebido pelo gelo para passar de – 10 oC até água
a te Q’ =
1000 + 16000 + 200te Q’
= 17000 + 200te.
Calor
retirado de m = 1000 g de água para passar de 20 oC até
te Q’’
= m.c.(te – to)
= 1000.1.(te – 20) Q’’
= 1000te – 20000.
Pelo
princípio da conservação da quantidade de calor Q’
+ Q’’ = 0 17000
+ 200te + 1000te – 20000 = 0 1200te =
3000 te =
3000/1200 te =
2,5 oC.
R- C
07- (UCPEL – RS - 2020)
O professor Paul Hewitt, do City College de San Francisco, objetivando explicar as características de uma curva de aquecimento para seus alunos e leitores, elaborou um gráfico, ilustrado na figura abaixo, que mostra o comportamento da temperatura de 1 g de água, inicialmente no estado sólido à temperatura de -50° C, em função do calor absorvido, quando essa massa de água está submetida a pressão de 1 atm.
Um estudante de Física, baseado nos conceitos cientificamente corretos sobre calorimetria, analisou o gráfico e fez as seguintes afirmativas:
I. O calor específico da água no estado líquido é 4,19 J/kg.K.
II. O calor latente de fusão da água é igual 80,0 J/g.
III. O calor latente de vaporização da água é igual 2260000,0 J/kg.
IV. A quantidade de calor latente absorvido pela água é igual a 620 cal.
Estão corretas apenas as afirmativas:
(A) I, II e III
(B) I e II
(C) II e IV
(D) III e IV
(E) II, III e IV
A seguir, um resumo da teoria:
Curva de aquecimento – calor sensível e calor latente
I. Falsa.
II. Falsa.
III. Correta.
IV. Correta.
Calor latente ocorre só na mudança de estado QL = 80 cal (fusão) + 540 cal (vaporização) = 620 cal
R- D
08- (UECE - Universidade Estadual do Ceará – 2020)
Dois blocos de materiais diferentes (ferro e concreto) e de mesma massa foram utilizados como amostras de um teste experimental.
Os mesmos foram aquecidos, a partir da temperatura ambiente, por fontes térmicas idênticas, que transmitiram a mesma quantidade de calor aos blocos.
Desconsiderando eventuais mudanças de estado, observou-se que o bloco de ferro sofreu maior variação de temperatura.
Com relação às propriedades térmicas dos materiais em pauta, tal fenômeno é explicado pelo fato de o bloco de ferro apresentar
A) maior calor específico comparado ao de concreto.
B) maior capacidade térmica que o de concreto.
C) a mesma capacidade térmica do bloco de concreto.
D) menor calor específico comparado ao de concreto.
Equação fundamental da calorimetria (calor sensível ou calor específico)
Denomina-se calor sensível ou calor específico (c) o calor que provoca uma variação na temperatura de um corpo, sem que ele mude de estado físico.
Verifica-se experimentalmente que a quantidade de calor (Q) recebida ou cedida por um corpo é diretamente proporcional à sua massa m e à sua variação de temperatura Δθ.
Matematicamente:
R-
D
09- (UERJ – RJ – 2020)
Para aquecer a quantidade de massa m de uma substância, foram consumidas 1450 calorias.
A variação de seu calor específico c, em função da temperatura θ, está indicada no gráfico.
O valor de m, em gramas, equivale a:
(A) 50
(B) 100
(C) 150
(D) 300
Equação fundamental da calorimetria (calor sensível ou calor específico)
R-
B
10- (Universidade Federal de Lavras – UFLA – MG – 2020)
Considere
duas substâncias X e Y, de massas iguais, com mesma temperatura
inicial e com calores específicos, tais que
.
Caso essas duas substâncias sejam aquecidas gradualmente com uma
mesma fonte de calor, o gráfico que representa a relação da temperatura de cada substância com o calor é o apresentado na alternativa:
Equação fundamental da calorimetria (calor sensível ou calor específico)
R- A
11- (UFPR – PR – 2020).
Um objeto de massa m = 500 g recebe uma certa quantidade de calor Q e, com isso, sofre uma variação de temperatura ∆T.
A relação entre ∆T e Q está representada no gráfico ao lado.
Assinale a alternativa que apresenta corretamente o valor do calor específico c desse objeto.
a) c = 2 J/g.°C.
b) c = 4 J/g.°C.
c) c = 8 J/g.°C.
d) c = 16 J/g.°C.
e) c = 20 J/g.°C.
Equação fundamental da calorimetria
Observe no gráfico que enquanto a temperatura do objeto de massa m = 500 g = 0,5 kg varia de, por exemplo, 0 oC a 60 oC a quantidade de calor (energia térmica) recebida é de (120 – 0) = 120 kJ = 120.103 J.
R- B
12- (Universidade Virtual do Estado de São Paulo – Univesp – 2020)
No dicionário, matéria é tudo aquilo que tem massa e ocupa lugar no espaço, ou qualquer substância que compõe um corpo sólido, líquido ou gasoso.
O estado físico da matéria está relacionado com as forças que atuam em seu interior.
A matéria pode apresentar-se em qualquer estado físico, conforme a pressão e temperatura.
Um esquema das mudanças de fase de uma substância é mostrado na Figura abaixo.
Considere os pontos I, II, III, IV, V e VI mostrados na Figura e assinale a alternativa correta em relação ao processo de mudança de fase da matéria.
a) O ponto indicado por I é chamado de fusão. Neste processo, há a adição de calor ao sistema e se a substância considerada for pura, a fusão do sólido ocorre à temperatura constante (ponto de fusão) b) A sublimação de uma substância pode ser representada pelo ponto VI. Este processo é dado pela passagem da substância da fase gasosa para a fase líquida e calor é retirado do sistema para que a sublimação ocorra
c) O ponto II representa o processo de vaporização, onde a substância passa do seu estado físico líquido para o estado gasoso. Este processo pode ser classificado em ebulição, evaporação e calefação. No processo de calefação, a vaporização ocorre de maneira lenta e natural, enquanto na ebulição e na evaporação a substância rapidamente muda de fase
d) A solidificação de uma substância é dada pela passagem da matéria em seu estado líquido para o estado sólido. Este processo é representado pelo ponto III e para que ele ocorra há a necessidade de adicionar calor ao sistema
e) Quando a matéria passa do estado líquido para o gasoso, processo chamado de vaporização (ponto II), as partículas no interior desta substância ficam mais próximas umas das outras, devido ao calor adicionado
Se você não domina a teoria, ela está a seguir:
Mudanças de estado físico da matéria
Características moleculares dos sólidos
Características moleculares dos líquidos
Características moleculares dos gases
Os gases não possuem forma própria e seu volume é variável, já que suas moléculas se deslocam em todas as direções e sentidos.
Observe pelo que foi fornecido acima que, se você quiser fazer com que um corpo mude de estado físico passando de sólido para líquido e depois para gasoso (tem que ser nessa ordem), ele deve receber calor, para aumentar o movimento vibratório de suas moléculas aumentando assim sua temperatura.
Do mesmo modo, a passagem gasoso, líquido e sólido (nessa ordem), só pode ocorrer se o corpo perder calor (diminuir sua temperatura).
Mudanças de estado físico
R- A
13- (Faculdade de Medicina de Marília - FAMEMA – SP – 2020)
Se 200 g desse óleo for aquecido nesse fogão durante um minuto, a temperatura desse óleo será elevada em, aproximadamente,
R- B
14- (FAMERP–SP - Faculdade de Medicina de São José do Rio Preto –- 2020)
Princípio das trocas de calor
São dados:
R- B
15- (Faculdade de Medicina do ABC – FMABC – SP – 2020)
Uma pessoa sempre usa um ebulidor para aquecer a mesma massa de água, provocando um aumento de temperatura Δθ, num intervalo de tempo Δt.
Certo dia em que estava com pressa, a pessoa utilizou dois ebulidores para o mesmo aquecimento, mas a potência do segundo ebulidor era apenas um terço da potência do primeiro.
Considerando que todo o calor gerado pelos dois ebulidores foi absorvido pela água e que não houve perda de calor para o meio externo, o tempo de aquecimento com o uso dos dois ebulidores, até que a água sofresse a mesma variação de temperatura Δθ, foi de
R-
E
16- (ENEM-MEC-019)
Em uma aula experimental de calorimetria, uma professora queimou 2,5 g de castanha-de-caju crua para aquecer 350 g de água, em um recipiente apropriado para diminuir as perdas de calor.
Com base na leitura da tabela nutricional a seguir e da medida da temperatura da água, após a queima total do combustível, ela concluiu que 50% da energia disponível foi aproveitada.
O
calor
específico da água é
,
e
sua
temperatura inicial era de
.
Qual foi a temperatura da água, em grau Celsius, medida ao final do experimento?
Pela tabela você observa que cada m = 10 g de castanha de caju para serem queimados necessitam de 70 kcal de calor e, assim a massa de m’ = 2,5 g necessitará de:
R
- C
17- (ESCOLA TÉCNICA ESTADUAL – ETEC – SP – 2020)
É
possível calcular a quantidade de calor trocada em um sistema por
meio da relação matemática:
.
Essa relação é conhecida como a Equação Fundamental da Calorimetria e mostra que o calor trocado (Q) depende da massa (m), do calor específico (c) e da variação de temperatura do corpo (∆T).
Sabendo que a massa da solução referida no texto é 100 g e considerando o calor específico como
,
a quantidade
de calor trocada nesse processo
é
(A) 60 calorias.
(B) 600 calorias.
(C) 2 200 calorias.
(D) 2 800 calorias.
(E) 5 000 calorias
R- B
18- (Instituto Federal de Educação, Ciência e Tecnologia do Paraná – IFPR – 2020)
Durante um experimento científico, um cientista descobreuma nova substância pura e resolve batizá-la de NinaLinaK2.
Ao aquecer a substância, obtém-se a curva de aquecimento, a qual está representada no diagrama abaixo.
Considerando que, durante todo o processo, a substância recebeu calor, mantendo a pressão constante, analise as alternativas abaixo e marque a correta.
A) NinaLinaK2 está sofrendo fusão entre os pontos 4 e 5.
B) Na temperatura T3, NinaLinaK2 está sofrendo vaporização.
C) Entre 3 e 4, NinaLinaK2 está no estado gasoso.
D) A quantidade de calor necessária para fundir a NinaLinaK2 é maior do que a quantidade de calor necessária para vaporizá-la.
Observe as informações fornecidas no gráfico abaixo:
Veja pelas dimensões fornecidas no gráfico que Q23 > Q45.
R- D
19- (Instituto Federal do Rio Grande do Sul – IFRS – RS – 2020)
Em uma panela de pressão coloca-se 1,0 L de água à temperatura de 20 ºC.
A panela é devidamente tampada, colocada sobre a chama de um fogão a gás e ali deixada até
ocorrer a total vaporização da água.
Considerando que a massa de 1,0 L de água é de 1000 g, o calor específico da água de 1,0 cal/(g°C) e o calor latente de vaporização de 540 cal/g, as quantidades de calor sensível e de calor latente trocados entre a chama e a água nesse processo, em kcal , respectivamente, foram
(A) 80; 540.
-(B) mais de 80; 540.
(C) menos de 80; 540.
(D) menos de 80; mais de 540.
(E) menos de 80; menos de 540.
(Equação fundamental da calorimetria (calor sensível ou calor específico)
Calor Latente
A água troca com a chama mais calor que esses valores obtidos (vapor sai pela válvula de segurança)
R- B
20- (PUC GOIÁS - 2020)
O município de Rio Quente (Goiás) abriga um importante polo de preservação ambiental do país e
possui o único rio de águas quentes do mundo.
A título de experiência, um turista estadunidense coloca em um balde 1,5 litros da água desse rio e mede sua temperatura em 113 °F.
Passados 2 minutos, ele volta a medir a temperatura da água e constata ser de 77 °F.
Assinale a alternativa correta que indica a perda de energia da água para o ambiente, no intervalo de tempo considerado:
A ( ) – 0,30 kcal.
B ( ) – 0,54 kcal.
C ( ) – 30 kcal.
D ( ) – 54 kcal.
Termometria
Equação fundamental da calorimetria (calor sensível ou calor específico)
R- C
21- (PUCCAMP – SP – 2020)
R- E
22- (PUC – Rio – 2020)
(A) 0,50
(B) 0,30
(C) 0,20
(D) 0,15
(E) 0,10
Princípio das trocas de calor
m1 = m2 = m3 = m
R- E
23- Universidade Estadual de Maringá (UEM) – PR - 2020
Um
cubo de gelo de
massa igual a
,
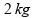à temperatura
inicial de
,
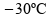é colocado em um forno de temperatura controlada e absorve
calor à razão constante de 2000 cal/min.
Sejam
,
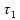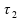e
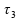períodos de tempo que se referem, respectivamente, ao 1)
tempo de aquecimento do gelo (antes da fusão);
2) tempo de fusão do gelo a 0º C;
e 3)
tempo de aquecimento da água (após a fusão) até que sua
temperatura alcance 30 ºC.
Considere que o
calor específico do gelo, o calor específico da água e o calor
específico latente de fusão do gelo sejam, respectivamente, iguais
a 0,50 cal/(g ºC), 1,00cal/(g º C) e 80,00 cal/g. Nessas
condições, assinale o que for correto.
01)
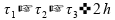
02)
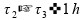
04)
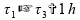
08)
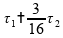
16)
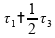
A quantidade de calor para aquecer uma amostra é dada por:
A quantidade de calor para mudar uma amostra de estado é dada por:
Vamos calcular a quantidade de calor em cada uma das etapas. Repare que as constantes fornecidas no enunciado estão com unidades em gramas, então convém utilizar a massa da amostra em gramas.
Para
a primeira etapa, a
quantidade de 2 kg (2000 g) é aquecida de
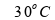a
:
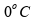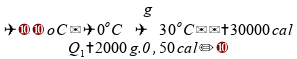
Para a segunda etapa, a quantidade de 2 kg (2000 g) passa do estado sólido para o líquido:
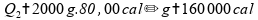
Para
a terceira e última etapa, a
quantidade de 2 kg (2000 g) é aquecida de
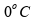a
:
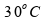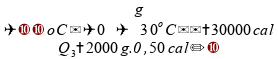
Podemos
calcular cada um dos tempos
,
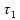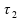e
,
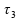sabendo que a energia fornecida ao sistema é de
:
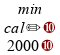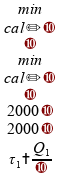
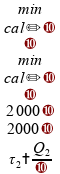
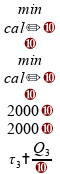
Vamos agora avaliar cada uma das alternativas.
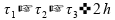
Se somarmos os intervalos de tempo, temos 2 horas:
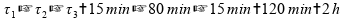
Invalidando esta alternativa.
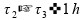
Se somarmos estes intervalos de tempo, temos mais de uma hora:
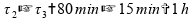
Invalidando esta alternativa.
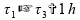
Se tomarmos estes intervalos de tempo, temos menos de uma hora:
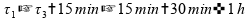
Invalidando esta alternativa.
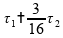
Se fizermos esta operação:
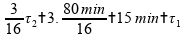
Logo, esta alternativa está correta.
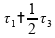
Como
sabemos
que
,
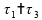esta alternativa é inválida.
Logo, somente a alternativa 16) está correta.
Termometria
24- (Escola de Especialistas de Aeronáutica – EEAR – 019/020)
Roberto, empolgado com as aulas de Física, decide construir um termômetro que trabalhe com uma escala escolhida por ele, a qual chamou de escala R. Para tanto, definiu – 20°R como ponto de fusão do gelo e 80°R como temperatura de ebulição da água, sendo estes os pontos fixos desta escala. Sendo R a temperatura na escala criada por Roberto e C a temperatura na escala Celsius, e considerando que o experimento seja realizado ao nível do mar, a expressão que relaciona corretamente as duas escalas será:
a) C = R – 20
b) C = R + 20
c) C = (R 20)/2
d) C = (R 20)/2
Relacionando as escala Celsius e R:
R- B
25- (Faculdade de Medicina do Hospital Israelita Albert Einstein-SP - 2020)
O gráfico mostra a relação entre as temperaturas de um mesmo corpo, lidas nas escalas Fahrenheit
(θF) e Celsius (θC).
Assim, sabendo que a temperatura média na superfície de Titã é de aproximadamente –180 ºC, essa
temperatura, expressa na escala Fahrenheit, corresponde a
(A) –102 ºF.
(B) –68 ºF.
(C) –292 ºF.
(D) –324 ºF.
(E) –412 ºF.
Nem é preciso utilizar o gráfico fornecido, basta utilizar a equação de conversão entre essas escalas, fornecida a seguir.
Relação entre as escalas
Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de
acordo com a relação matemática baseada no teorema de Thales:
R- C
26- (UERJ – RJ – 2020)
Com o aumento do efeito estufa, uma chuva ácida pode atingir a temperatura de 250 ºC.
Na escala Kelvin, esse valor de temperatura corresponde a:
(A) 212
(B) 346
(C) 482
(D) 523
Relação entre as escalas
Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir,
de acordo com a relação matemática baseada no teorema de Thales:
R- D
27- (PUC-SP-2020)
O gráfico a seguir, descreve o comportamento da temperatura de uma amostra de certo material, em função do tempo.
Determine, na escala Fahrenheit, a variação de temperatura sofrida pela amostra, desde 1h30min até 5h30min.
A) 40
B) 55
C) 72
D) 90
Converter temperaturas de uma escala para a outra não é o mesmo
que converter intervalos de temperatura entre as escalas
R- C
28- (UFJF – MG – 2020)
Em uma aula sobre escalas de temperatura, termômetros sem escala foram fornecidos aos alunos de dois grupos, A e B, para que criassem suas próprias escalas lineares.
Ambos os grupos tomaram como pontos fixos a fusão do gelo e a ebulição da água.
Para a fusão do gelo, o grupo A atribuiu o valor 0, e o grupo B atribuiu o valor 10.
Para a ebulição da água, o grupo A atribuiu o valor 100, e o grupo B atribuiu o valor 30.
Se
a temperatura para o grupo A é representada por
,
e para o grupo B ela é representada por
qual é a relação termométrica entre estas duas escalas?
(A) TA = 100TB + 20
(B) TA = 20TB – 200
(C) T+ = 5TB
(D) TA = 100TB – 20
(E)TA = 5TB – 50
Termometria
Vamos adaptar a demonstração acima para o caso do exercício cujos pontos fixos estão na figura abaixo:
R- E
29- Universidade Federal de Uberlândia – UFU – MG – meio do ano - 2019/2020
Os termômetros são equipamentos construídos para realizar medidas de temperatura de forma indireta.
O termômetro é montado para utilizar uma propriedade física cujas variações estão associadas à temperatura, chamada de propriedade termométrica.
O valor da temperatura é determinado e indicado em função da situação física detectada, sendo que, para efeitos de calibração, se faz necessário o uso de referências ou de padrões.
Qual das alternativas possui propriedades físicas que podem ser utilizadas para construção de termômetros para realizar medidas de variações de temperaturas?
A) Resistência elétrica de um fio condutor e pressão de um gás a volume constante.
B) Diferença de potencial entre dois metais diferentes em contato e velocidade de propagação de uma onda eletromagnética no vácuo.
C) Emissão de radiação eletromagnética por um corpo sólido e ponto triplo da água.
D) Velocidade do som no ar e massa de um objeto sólido.
Substâncias termométricas e grandezas termométricas
A temperatura é um número que está associado ao grau, nível de vibração (energia cinética) das moléculas de um corpo e, como não se pode medir a vibração de cada molécula de um corpo isoladamente, pode-se medir sua temperatura de maneira indireta utilizando certas substâncias que possuam uma dada grandeza que varie com a temperatura.
Essas substâncias recebem o nome de substâncias termométricas e a grandeza que varia com a temperatura recebe o nome de grandeza termométrica.
Exemplos:
Régua
metálica 
quando aquecida
sofre um aumento em
seu comprimento. A substância
termométrica é a régua metálica e a grandeza termométrica, seu comprimento, que varia com a temperatura.
No termômetro de resistência de platina a grandeza termométrica é a resistência elétrica de um fio
desse metal e a substância termométrica é a platina.
R- A
Dilatometria
30- (CEDERJ-RJ-2020)
Na construção de ferrovias, é necessário deixar uma folga entre os trilhos para permitir que eles se dilatem caso a temperatura aumente. Suponha que cada trilho tem 20 m de comprimento na temperatura média da região onde serão
Dilatação linear dos sólidos
R- B
31- (Instituto Federal de Educação, Ciência e Tecnologia de Pernambuco – IFPE – 2020)
Com relação aos fenômenos da Dilatação Térmica, analise as afirmativas abaixo.
II. Quando aquecemos um recipiente metálico totalmente preenchido com um líquido, verificamos o transbordamento do líquido correspondente à dilatação real sofrida por ele.
III. No caso de aquecimento de recipiente metálico totalmente preenchido com um líquido, ocorre transbordamento desse líquido, pois a expansão provocada por ele é maior que o ocorrido com o recipiente metálico.
Estão CORRETAS, apenas, as afirmativas.
I. Correta
II. Falsa
Dilatação dos líquidos
Veja acima que ∆VR = ∆Vap + ∆Vf
III. Correta
Veja informação acima
IV. Falsa
Como o coeficiente de dilatação do parafuso é maior que o da chapa o parafusa se dilata mais que a chapa não conseguindo ser inserido na mesma.
V. Correta
A dilatação anômala da água ocorre quando sua temperatura varia entre 0°C e 4°C, intervalo no qual há um fenômeno inverso ao natural e esperado. Neste intervalo de temperatura a água, ao ser resfriada, sofre uma expansão no seu volume, e ao ser aquecida, uma redução.
R - E
32- (Insper – SP – 2020)
O termostato é um dispositivo cuja função primordial é não deixar a temperatura de um sistema exceder um valor predeterminado.
Pode ser utilizado em refrigeradores, sistemas de arrefecimento de motores de veículos etc. Dentre os modelos existentes no mercado, há o termostato mecânico, que usa o princípio do par bimetálico ou lâmina bimetálica.
O par bimetálico é composto por duas lâminas de metais de diferentes coeficientes de dilatação, que têm suas faces firmemente soldadas. As figuras 1 e 2 mostram a vista de perfil de um par bimetálico.
Na figura 1, o par bimetálico encontra-se à temperatura ambiente e em formato de superfície plana; na figura 2, após sofrer uma variação em sua temperatura, o par está curvado, com a face côncava na lâmina do metal B e a face convexa na lâmina do metal A.
Na figura 2, em relação à figura 1,
(A) o par bimetálico teve sua temperatura (A) diminuída, e o coeficiente de dilatação linear de A é maior do que o coeficiente de dilatação linear de B.
(B) aumentada, e o coeficiente de dilatação linear de A é menor do que o coeficiente de dilatação superficial de B.
(C) diminuída, e o coeficiente de dilatação linear de A é menor do que o coeficiente de dilatação linear de B.
(D) aumentada, e o coeficiente de dilatação linear de A é menor do que o coeficiente de dilatação linear de B.
(E) diminuída, e o coeficiente de dilatação superficial de A é maior do que o coeficiente de dilatação superficial de B.
Dilatação linear
Observe na expressão acima que:
A dilatação linear ΔL é diretamente proporcional à variação de temperatura Δt.
A dilatação linear ΔL é diretamente proporcional ao comprimento inicial Lo.
A dilatação linear ΔL depende do material de que é constituído o corpo.
Assim, quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação, quando aquecida e para o lado da barra de maior coeficiente de dilatação, quando resfriada.
R- C
Termodinâmica
Transformações gasosas
01- (IFG - Instituto Federal de Educação, Ciência e Tecnologia de Goiás – 2020)
A charge aborda as mudanças de estados físicos pelas quais a água passa.
Essas mudanças são muito importantes para o ciclo da água. A respeito desses processos, podemos afirmar que:
a) No terceiro quadrinho observa-se o fenômeno de sublimação, no qual a água passa da fase líquida para a fase gasosa, formando as nuvens.
b) Durante o processo de solidificação, as moléculas de água se afastam umas das outras, fazendo com que o gelo tenha maior densidade que a água no estado líquido.
c) O derretimento de geleiras, causado pelo aquecimento global, tem afetado o equilíbrio do planeta, comprometendo a sobrevivência dos ursos polares.
d) Durante o processo de condensação, a água passa do estado sólido para o líquido. Nesse estado, a água assume a forma do objeto que a contém.
a) Falsa - A sublimação é a mudança do estado sólido para o estado gasoso, sem passar pelo estado líquido.
b) Falsa – o gelo tenha menor densidade que a água no estado líquido, por isso, flutua.
c) Correta
d) Falsa - Condensação é uma das fases em que ocorre a transformação da matéria, do estado gasoso para o estado líquido.
R- C
02- (Universidade Federal de Lavras – UFLA – MG – 2020)
Uma panela de pressão é um utensílio doméstico utilizado para o cozimento dos alimentos em altas temperaturas.
Ela é composta por uma tampa que veda parcialmente o seu interior, impedindo o escapamento de vapor.
Ao fornecer calor à água em seu interior, o ar aprisionado aquece-se, provocando um aumento da pressão interna da panela, o que consequentemente eleva a temperatura de ebulição da água.
O resultado disso é que a água ferve a uma temperatura acima de 100°C, tornando o cozimento de alimentos mais rápido.
Considerando o vapor de água dentro da panela como se fosse um gás ideal, o gráfico que relaciona duas das grandezas físicas envolvidas no processo até a ebulição da água é o apresentado na alternativa:
Transformação isocórica, isométrica ou isovolumétrica
Nessa transformação o volume é mantido constante.
Os físicos Jacques Charles e Gay-Lussac descobriram experimentalmente que, numa transformação isocórica, a pressão (P) é diretamente proporcional à temperatura absoluta (T), ou seja:
Veja o gráfico PxT à direita acima.
R- A
03- (Faculdade de Medicina do ABC – FMABC – SP – 2020)
O pneu de um automóvel foi calibrado à temperatura ambiente, mas, depois de trafegar durante certo tempo, a temperatura do ar no interior do pneu aumentou.
Considerando que o ar se comporte como um gás ideal, que não houve vazamento de ar do pneu e que o volume do pneu não variou, pode-se afirmar, sobre o ar no interior do pneu, que
(A) sua pressão aumentou e sua densidade diminuiu.
(B) sua pressão aumentou e sua densidade não variou.
(C) sua pressão diminuiu e sua densidade não variou.
(D) sua pressão aumentou e sua densidade também aumentou.
(E) sua pressão diminuiu e sua densidade também diminuiu.
Transformação isocórica, isométrica ou isovolumétrica
Como nessa transformação a pressão é diretamente proporcional à temperatura, se a temperatura aumenta, a pressão interna do pneu também aumentará.
Sendo
a densidade do ar no interior do pneu densidade =
e sendo a massa de ar a mesma, e o volume o mesmo, a densidade do ar
também será a mesma.
R- B
04- (ESCOLA TÉCNICA ESTADUAL – ETEC – SP – 2020)
Durante uma reação química realizada em meio aquoso, observa-se a variação da temperatura do sistema de 22 ºC para 28 ºC
Conclui-se, corretamente, que se trata de uma reação
(A) exotérmica, pois cedeu calor para o sistema.
(B) exotérmica, pois absorveu calor do sistema.
(C) endotérmica, pois cedeu calor para o sistema.
(D) endotérmica, pois absorveu calor do sistema.
(E) isotérmica, pois não houve troca de energia.
Todas as reações químicas e bioquímicas liberam ou absorvem energia do ambiente de alguma forma.
Os processos que liberam calor são denominados exotérmicos e nos transmitem sensação de aquecimento. A temperatura final dos produtos é maior que a temperatura inicial dos reagentes.
Os processos que absorvem calor são denominados endotérmicos e nos transmitem sensação de resfriamento.
A temperatura dos produtos finais é menor que a dos reagentes.
R- A
05- (FPS-Faculdade Pernambucana de Saúde-PE-2020)
Um mol de um gás monoatômico ideal sofre a transformação mostrada no diagrama P-V abaixo.
Determine a relação entre as temperaturas nos estados A e C.
A) TA = 0,5.TC
B) TA = 1,0.TC
C) TA = 1,5.TC
D) TA = 2,0.TC
E) TA = 2,5.TC
Equação geral dos gases perfeitos
À equação acima se dá o nome de lei geral dos gases perfeitos e você deve utiliza-la quando houver variação de pressão, volume e temperatura simultaneamente, mantendo-se constante a massa.
R- D
06- (Instituto Federal de Educação, Ciência e Tecnologia Fluminense – IFF – 2020)
Maria está fazendo uma experiência com um gás ideal.
O
gás
está confinado em um recipiente e, inicialmente, sua temperatura,
pressão e volume são, respectivamente,
.
Ela então realiza dois processos com o gás.
Primeiro, ela o comprime até que seu volume e sua pressão tenham a metade do valor inicial.
No
segundo processo, ela expande o gás até o volume inicial
,
mantendo a temperatura constante durante a expansão.
Depois desses processos, qual valor Maria encontrará ao medir a pressão do gás?
R- A
Princípios da Termodinâmica
07- (Faculdade de Ciências Médicas da Santa Casa de São Paulo – SP – 2020)
O diagrama P × V mostra as transformações isotérmica (AB), isovolumétrica (BC) e isobárica (CD) sofridas por certa massa de gás ideal.
A energia interna do gás diminuiu
(A) apenas nas transformações AB e BC.
(B) apenas nas transformações BC e CD.
(C) apenas na transformação CD.
(D) apenas na transformação AB.
(E) em todas as transformações
Se você não domina a teoria, ela está a seguir:
Primeiro princípio da termodinâmica aplicado numa transformação Isotérmica
Primeiro princípio da termodinâmica aplicado numa transformação Isobárica
Primeiro princípio da termodinâmica aplicado numa transformação Isocórica, Isométrica ou Isovolumétrica
R- B
08- (UDESC - Universidade do Estado de Santa Catarina – 2020)
Considere a Figura abaixo que descreve os ciclos termodinâmicos ABCD e ACD.
Analise as proposições em relação à Figura.
I. O trabalho realizado sobre o sistema para ir de A a D é igual a percorrer o ciclo pelos caminhos ABCD e ACD.
II. A variação da energia interna entre B e C e entre D e A é dada somente por troca de calor entre o sistema e o seu entorno.
III. Em qualquer ciclo fechado, conforme mostra a Figura 5, o calor total é igual ao trabalho total ao longo do ciclo.
IV. O ciclo ABCD é composto por duas transformações isobáricas e duas isocóricas.
V. O trabalho para ir de A a B pode ser calculado pela área delimitada por ABCD.
Assinale a alternativa correta.
A. ( ) Somente as afirmativas I, II e III são verdadeiras.
B. ( ) Somente as afirmativas I, III e V são verdadeiras.
C. ( ) Somente as afirmativas I, III e IV são verdadeiras.
D. ( ) Somente as afirmativas II, IV e V são verdadeiras.
E. ( ) Somente as afirmativas II, III e IV são verdadeiras.
I. Falsa
Principais características da transformação cíclica
Veja que as áreas dos ciclos ABCDA (A1) e ACDA (A2) são diferentes e consequentemente o trabalho
realizado em cada ciclo também é diferente.
II. Correta
Nesses dois trechos BC e DA a transformação é isovolumétrica (volume constante) cujas características estão a seguir.
Primeiro princípio da termodinâmica aplicado numa transformação Isocórica, Isométrica ou Isovolumétrica
III. Correta
IV. Correta
AB
e CD
isobáricas
BD
e CA
isocóricas (isométricas ou isovolumétricas)
V. Falsa
É calculado pela área A da figura abaixo e não pela área do ciclo
R- E
09- (Universidade Estadual do Oeste do Paraná – UNIOESTE – 2020)
O segundo princípio da Termodinâmica assegura que é impossível construir uma máquina térmica
operando em ciclos cujo único efeito seja retirar calor de uma fonte e convertê-lo integralmente em trabalho.
Considerando as consequências deste princípio é CORRETO afirmar que:
a) máquinas térmicas são dispositivos que convertem energia mecânica em energia térmica por meio da realização de trabalho e consumo de calor.
b) o rendimento de uma máquina térmica será de 100% quando o calor retirado da fonte em cada ciclo de operação da máquina for nulo.
c) o rendimento de uma máquina térmica nunca pode chegar a 100%, pois nenhuma máquina térmica consegue transformar integralmente calor em trabalho.
d) qualquer máquina térmica retira calor de uma fonte quente e rejeita integralmente esse calor para uma fonte fria após realizar um trabalho mecânico.
e) uma máquina térmica que realiza uma transformação cíclica retornando ao estado inicial, depois de efetuar todos os processos termodinâmicos do ciclo, tem rendimento de 100%.
Segundo Princípio da Termodinâmica
Pode-se definir o Segundo Princípio da Termodinâmica da seguinte maneira: “É impossível obter uma máquina térmica que, operando em ciclos, seja capaz de transformar totalmente o calor por ela recebido em trabalho”
É impossível transformar calor de uma fonte quente (Qq) em energia útil (trabalho W) sem que ocorra perdas para a fonte fria Qf).
Você pode reduzir essas perdas, por exemplo, diminuindo os atritos, mas nunca eliminá-las totalmente.
Se você conhecer o quanto de trabalho (W) a máquina térmica produz e o quanto de calor (Q) foi fornecido pela fonte quente, você pode calcular o rendimento (η) de uma máquina térmica.
Rendimento
(η) de
uma máquina térmica 
η = 
Observe na expressão acima que a eficiência (rendimento) da máquina térmica é sempre menor do que 1 (100%).
R- C
10- (Faculdade de Medicina de Jundiaí - FMJ –SP – 2020)
O diagrama pressão versus volume mostra a transformação cíclica ABCDA pela qual passa certa massa de gás ideal.
Em um ciclo, a variação da energia interna do gás é igual a
Transformação cíclica
Consiste numa série de transformações gasosas na qual o estado inicial coincide com o estado final, com o gás retornando à mesma pressão, volume e temperatura iniciais.
Toda transformação cíclica deve obedecer à seguinte condição:
Como as
temperaturas final e inicial são coincidentes (Ti =
Tf), a variação
de energia interna (ΔU) é nula 
ΔU
= 0.
R- C
11- (CEDERJ – RJ – meio do ano – 019/029)
Uma amostra de gás ideal está contida em um cilindro metálico que está imerso em uma grande quantidade de água a temperatura constante. O gás é comprimido lentamente numa transformação isotérmica.
A variação da energia interna do gás (ΔU) e o trabalho W realizado pelo gás nesse processo são:
(A) ΔU = 0; W > 0
(B) ΔU = 0; W < 0
(C) ΔU > 0; W > 0
(D) ΔU < 0; W < 0
Transformação isotérmica
Como a temperatura (T) e a energia interna (U) de um sistema estão associadas à energia cinética das moléculas, se a temperatura for constante (transformação isotérmica), a energia interna (U) do sistema também será constante.
Assim, a variação de energia interna (ΔU) do sistema será nula.
Transformação
isotérmica 
ΔU
= 0 
ΔU = Q – W
0 = Q – W Q
= W.
Q =
W Portanto,
numa transformação
isotérmica (temperatura
constante) todo
calor Q recebido pelo sistema é totalmente transformado em trabalho.
Como o gás é comprimido o trabalho realizado é negativo. (W < 0).
R- B
12- (CEDERJ-RJ-2020)
Considere um tubo vertical fechado na extremidade inferior que aprisiona um gás ideal em seu interior por meio de um leve êmbolo situado na extremidade oposta.
Lentamente, o êmbolo é pressionado até que o volume do gás se reduz à metade.
Considere duas formas de fazer isso.
No processo I, o tubo é mantido em contato térmico com um grande recipiente com água.
No processo II, o tubo é isolado termicamente do ambiente.
As descrições dos processos I e II e a avaliação das variações de energia interna correspondem a: (A) Processo I: compressão isotérmica; Processo II: compressão adiabática; A energia interna do gás aumenta nos dois processos.
(B) Processo I: compressão adiabática; Processo II: compressão isotérmica; A energia interna do gás aumenta nos dois processos.
(C) Processo I: compressão isotérmica; Processo II: compressão adiabática; A energia interna do gás aumenta somente no segundo processo.
(D) Processo I: compressão adiabática; Processo II: compressão isotérmica; A energia térmica do gás aumenta somente no segundo processo.
No
processo I sendo grande a quantidade de água a temperatura do gás é
a mesma que a da água (constante) e está sendo comprimido
trata-se
de uma compressão isotérmica (a
temperatura constante).
No
processo II como ele é isolado termicamente ele não troca calor com
o ambiente (transformação
adiabática) e está
sendo comprimido
trata-se
de uma compressão adiabática.
A energia interna do gás está relacionada com a variação da temperatura do mesmo e no primeiro processo, como a temperatura é constante a energia interna do gás permanece constante.
No segundo processo (transformação adiabática) a teoria está a seguir:
Transformação adiabática
Nela, o sistema não troca calor com o meio externo (Q = 0) e isso ocorre porque o gás está termicamente isolado ou porque a transformação é muito rápida de modo que qualquer troca de calor com possa ser considerada.
Se
Q = 0 ΔU
= Q – W
ΔU = 0 – W ΔU
= – W.
Então, todo o trabalho realizado pelo pistão é transformado em energia interna.
R- C
13- (FDSBC-SP-2020)
Um motor a combustão, movido a etanol, cuja massa específica é de 0,789 g/cm³ e calor de combustão igual a 6 400 kcal/kg, consome 5 litros a cada 30 minutos de funcionamento em regime constante.
Nessa condição, ele desenvolve uma potência útil de 23 565 W.
Determine, em porcentagem, o rendimento aproximado desse motor. Adote 1 cal=4,2J.
A) 36
B) 38
C) 40
D) 42
Regra de três
R- C
14- (EsPCEx - AMAN – SP - RJ – 2020)
Um gás ideal é comprimido por um agente externo, ao mesmo tempo em que recebe calor de 300 J de uma fonte térmica.
Sabendo-se que o trabalho do agente externo é de 600 J, então a variação de energia interna do gás é
Se você não domina a teoria, veja o resumo a seguir:
Primeiro Princípio da Termodinâmica ou Princípio da Conservação da Energia
Energia interna de um gás perfeito
Primeiro Princípio da Termodinâmica ou Princípio da Conservação da Energia
Trabalho positivo ou trabalho negativo
Na expressão W = P.(V – Vo), como a pressão P é sempre positiva:
Se V
> Vo 
W
> 0 
o sistema
(gás) em expansão
realiza trabalho sobre o meio exterior (ambiente).
Se V
< Vo W
< 0
o meio
exterior (ambiente) realiza trabalho sobre o sistema (gás).
Como
o gás recebe calor da fonte térmica
Q = + 300 J
Se
o gás ideal é comprimido por um agente externo (volume final menor
que volume inicial) o trabalho é negativo e o meio
exterior (ambiente) realiza trabalho sobre o sistema (gás)
W = - 600 J.
= Q – W
= 300 – (-600) = 300 + 600
= 900 J.
R- A
15- (FUVEST- SP- 2020 – Segunda Fase)
a)
Transformação adiabática
Exemplo prático
Na figura abaixo, trata-se de uma expansão adiabática (muito rápida e sem troca de calor com o meio
b)
16- (Instituto Federal de Educação, Ciência e Tecnologia Fluminense – IFF – 2020)
A figura a seguir representa o ciclo de um motor a combustão patenteado por Rudolf Diesel.
Ele é composto por dois processos adiabáticos, um isovolumétrico e um isobárico.
Qual é a eficiência de um motor construído com esse ciclo em que o módulo do calor trocado no processo isobárico é de 800 J e o módulo do calor trocado no processo isovolumétrico é de 300 J?
Rendimento de uma máquina térmica de Carnot
R - D
17- (Instituto Militar de Engenharia – IME – 2020)
Um escritório de patentes analisa as afirmativas de um inventor que deseja obter os direitos sobre três máquinas térmicas reais que trabalham em um ciclo termodinâmico. Os dados sobre o calor rejeitado para a fonte fria e o trabalho produzido pela máquina térmica – ambos expressos em Joules – encontram-se na tabela abaixo.
As afirmativas do inventor são:
Afirmativa 1: O rendimento das máquinas A e C são os mesmos para quaisquer temperaturas de fonte quente e de fonte fria.
Afirmativa 2: As máquinas A, B e C obedecem à Segunda Lei da Termodinâmica.
Afirmativa 3: Se o calor rejeitado nas três situações acima for dobrado e se for mantida a mesma produção de trabalho, a máquina B apresentará rendimento superior aos das máquinas A e C, supondo atendidos os princípios da termodinâmica.
Tomando sempre as temperaturas dos reservatórios das fontes quente e fria das máquinas como 900 K e 300 K, está(ão) correta(s) a(s) afirmativa(s):
(A) 1, apenas.
(B) 2, apenas.
(C) 1, 2 e 3.
(D) 1 e 3, apenas.
(E) 2 e 3, apenas.
Começando pela afirmativa 1, precisamos nos lembrar de como se calcula o rendimento de uma máquina térmica:
Não se esqueça que o calor da fonte quente é a soma do trabalho produzido com o calor da fonte fria (calor rejeitado).
Calculando o rendimento para a máquina térmica A:
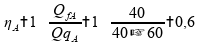
Calculando o rendimento para a máquina térmica C:
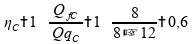
Por definição, e como podemos visualizar nas fórmulas, o rendimento da máquina térmica real não irá depender das temperaturas. Portanto, para todas as temperaturas o rendimento será o mesmo, o qual já foi calculado para a máquina A e C. Afirmativa 1 é verdadeira.
Para a afirmativa 2 vamos nos lembrar o que a Segunda Lei da Termodinâmica nos diz:
Ou seja, não importa a máquina térmica, o seu rendimento nunca será 100%. Em seus estudos Carnot enunciou que nenhuma máquina térmica real poderia ter eficiência maior ou igual ao do Ciclo de Carnot, para assim não violar a segunda lei. Vamos calcular a eficiência desse ciclo ideal:
Realizando o cálculo utilizando as temperaturas das fontes fria e quente:
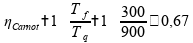
Já observamos o rendimento de 60% para as duas máquinas térmicas anteriores, vamos calcular para a máquina B:
Calculando o rendimento para a máquina térmica B:
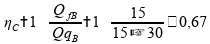
Então a máquina B não obedece à segunda lei, pois seu rendimento é igual ao do Ciclo de Carnot. Afirmativa 2 é falsa.
Para a afirmativa 3 precisamos recalcular os rendimentos, agora levando em consideração que o calor rejeitado nas máquinas A, B e C será dobrado:
Recalculando o rendimento para a máquina térmica A:
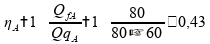
Recalculando o rendimento para a máquina térmica B:
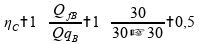
Calculando o rendimento para a máquina térmica C:
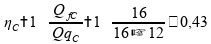
O rendimento da máquina B ainda será maior que todas as outras, portanto a afirmativa 3 está correta.
Após analisar todas as afirmativas concluímos que a alternativa correta é a D.
18- (MACKENZIE – SP – 2020)
A segunda lei da Termodinâmica afirma, em sucintas palavras, que não há a possibilidade de converter integralmente calor em trabalho.
Esquematicamente, a figura abaixo revela como funciona uma máquina térmica.
Considerando-se que o trabalho realizado nessa máquina valha 1,2 kJ e que a parte energética rejeitada para a fonte fria valha dois quintos da recebida da fonte quente, é correto afirmar que o rendimento da máquina retratada na figura e a parte energética rejeitada (em kJ) valem, respectivamente,
a) 40% e 1,2
b) 60% e 0,80
c) 40% e 1,0
d) 60% e 1,2
e) 40% e 0,60
Rendimento de uma máquina térmica de Carnot
R-
B
19- (PUC – Rio – 2020)
Considere as três afirmativas abaixo, em relação a um gás ideal.
I - Em uma compressão adiabática, a temperatura final do gás não pode ser maior do que a inicial, pois nenhum calor é trocado com a vizinhança.
II - Em um processo isocórico (isovolumétrico), nenhum trabalho é realizado pelo gás.
III - Em um processo isobárico, o trabalho realizado pelo gás é proporcional ao quadrado da variação do volume.
Marque a única opção CORRETA:
(A) Somente a afirmativa I é verdadeira.
(B) Somente a afirmativa II é verdadeira.
(C) Somente a afirmativa III é verdadeira.
(D) Somente as afirmativas I e II são verdadeiras.
(E) Somente as afirmativas I e III são verdadeiras.
I. Falsa
Leia atentamente as informações a seguir as aplicações práticas de algumas transformações adiabáticas:
Na figura da esquerda abaixo, ao levantar o pistão da bomba de bicicleta, você diminui a pressão interna o que faz abrir uma válvula localizada abaixo do pistão, fazendo o ar externo penetrar no cilindro.
Ao empurrar o pistão para baixo o aumento de pressão interna fecha automaticamente a válvula de entrada e abre a válvula de saída ligada ao pneu forçando o ar a penetrar no mesmo. Ao levantar o pistão novamente você começa tudo novamente.
Observe que, cada vez que você bombeia o ar no pneu, a bomba se aquece mais, o que ocorre principalmente porque você está forçando as moléculas de ar ficar mais próximas umas das outras, fazendo com que esse trabalho de compressão do gás (negativo) aumente a energia interna (ΔU), aumentando consequentemente a temperatura do gás.
Isso ocorre porque essa transformação é adiabática (não troca calor com o ambiente, pois é muito rápida) e obedece à função ΔU= – W.
Na figura
da direita (acima), trata-se
de uma expansão
adiabática (muito
rápida e sem troca de calor com o meio ambiente), onde Q = 0 e ΔU =
Q – W
ΔU = 0 – W ΔU
= – W
o volume
do gás aumenta (trabalho positivo) fazendo com que a energia interna
(ΔU) fique negativa e diminua, diminuindo assim, a pressão e a
temperatura e a pressão, e o gás resfria.
Leia atentamente as informações da figura da esquerda acima (compressão) adiabática que, apesar de o gás não trocar calor com o ambiente após a compressão a temperatura do gás aumenta.
II. Correta
Transformação isocórica, isométrica ou isovolumétrica
Ocorre
a volume
constante Vo =
V
ΔV = 0 W
= P.ΔV
W = P.0 W
= 0 ΔU
= Q – W ΔU
= Q – 0 ΔU
= Q
III. Falsa
Transformação isobárica
Ocorre à pressão constante. A variação de temperatura (ΔT) provoca uma variação de energia interna (ΔU) do sistema e a variação de volume (ΔV) produz trabalho.
Parte do calor (Q) recebido pelo sistema é armazenada sob forma de energia interna e parte é transformada em trabalho, de modo que ΔU = Q – W.
R- B