 figura
2
figura
2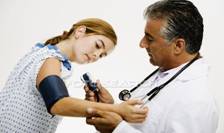 figura
3
figura
3
VETORES
Diferenças entre grandezas escalares e grandezas vetoriais
Grandezas escalares
São aquelas que ficam perfeitamente caracterizadas por um número seguido de uma unidade. Exemplos: As grandezas abaixo ficam claramente determinadas quando delas fornecemos um número real de medida e a unidade de medida.
figura
1 figura
2
figura
2 figura
3
figura
3
figura
4 figura
5
figura
5
Assim, por exemplo, a temperatura onde estão os ursos da figura 1 é de -10oC, a pressão da garota da figura 2 é de 13mmHg por 8mmHg, o homem está olhando seu relógio que marca 8,00 horas, o reservatório de água da figura 4 tem volume de 1,5.106 litros e a massa do produto da figura 5 é de 500g. Todas elas são grandezas escalares que ficam claramente determinadas quando delas fornecemos um número real de medida e a unidade de medida.
Grandezas vetoriais
Não ficam perfeitamente definidas apenas pelo número acrescido de unidade. Para entendê-las, considere um motociclista que está a 5m de uma ponte que caiu.
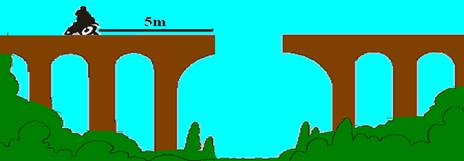

Se você afirmar que a moto se deslocou 5,5m você não pode dizer que ela cairá, pois ela pode se deslocar 5,5m para o leste ou para o oeste. Assim, o deslocamento da moto não ficou perfeitamente definido pelo número acrescido de unidade, pois faltou a orientação (direção e sentido).
Então, o deslocamento é uma grandeza vetorial, que são aquelas que, além do número e da unidade, para ficarem perfeitamente caracterizadas necessitam também de uma direção e de um sentido.
Exemplos de grandezas vetoriais: deslocamento, velocidade, aceleração, força, impulso, etc.
Vetor
Trata-se da representação de uma grandeza vetorial que é feita através de um segmento de reta orientado, cujo sentido é fornecido pela seta, em uma de suas extremidades.
Todo vetor é representado por letras acompanhadas por uma pequena seta sobre elas.

![]() -
lê-se “vetor P”
-
lê-se “vetor P” ![]()
![]() -
lê-se “vetor Q”
-
lê-se “vetor Q”
Características de um vetor
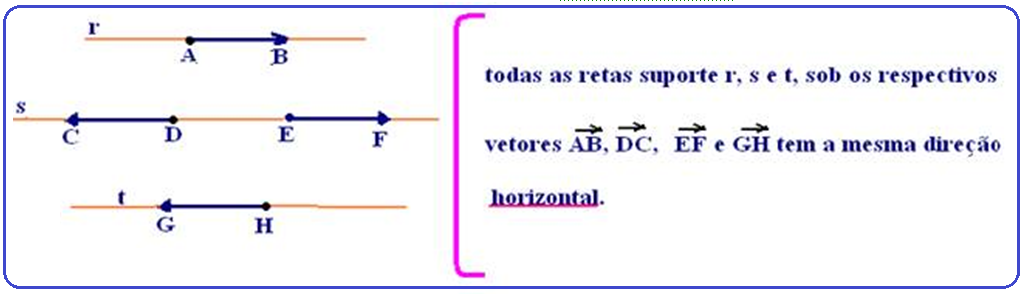
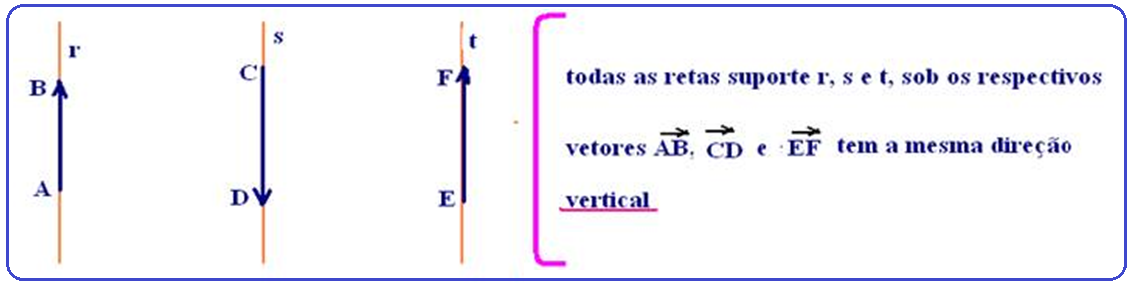
![]() Direção
Direção ![]() localização
no espaço,
fornecida pela reta
suporte (S) do segmento.
Exemplos:
localização
no espaço,
fornecida pela reta
suporte (S) do segmento.
Exemplos:
Sentido ![]() dado
pela seta.
Exemplos:
dado
pela seta.
Exemplos:

Intensidade
ou módulo ![]() composto
pelo número e pela unidade de medida,
ou seja, pelo comprimento
do segmento, numa certa escala adotada. A
intensidade
de um vetor
composto
pelo número e pela unidade de medida,
ou seja, pelo comprimento
do segmento, numa certa escala adotada. A
intensidade
de um vetor ![]() costuma ser representada por P (sem a seta) ou por
costuma ser representada por P (sem a seta) ou por ![]() e
lê-se “intensidade ou módulo do vetor
e
lê-se “intensidade ou módulo do vetor ![]() ”
”
Exemplos
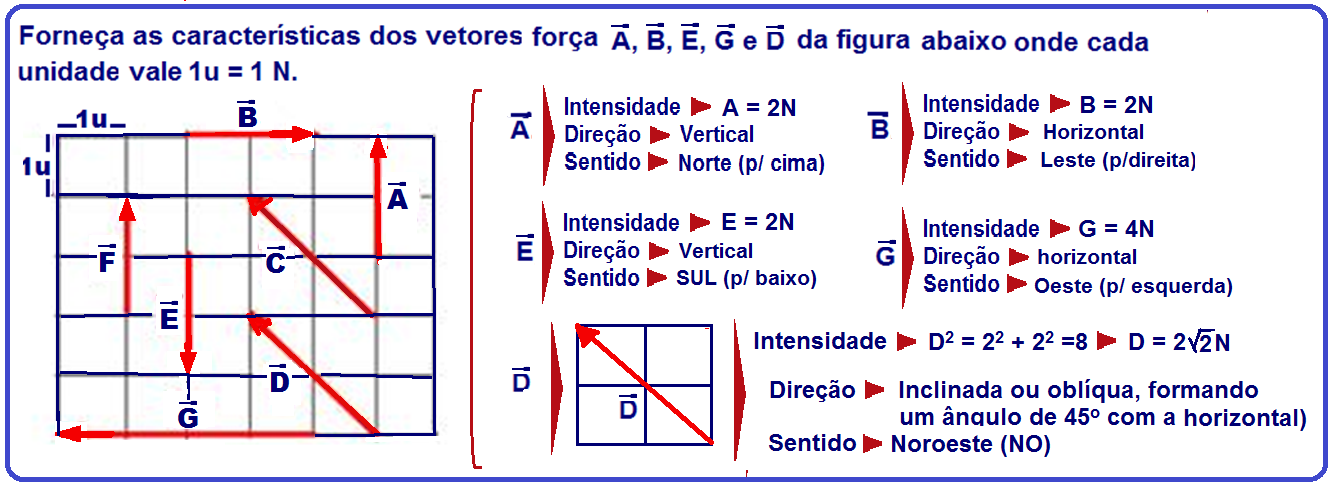
O que você deve saber
![]() Na intensidade
não
se deve escrever
Na intensidade
não
se deve escrever ![]() = 20m/s, mas sim
V = 20m/s (sem a seta)
= 20m/s, mas sim
V = 20m/s (sem a seta)
![]() Um vetor
nulo
deve ser representado da seguinte maneira
Um vetor
nulo
deve ser representado da seguinte maneira ![]() =
=![]()
A direção de um vetor também pode ser definida como sendo o ângulo que ele forma com a horizontal ou a vertical.
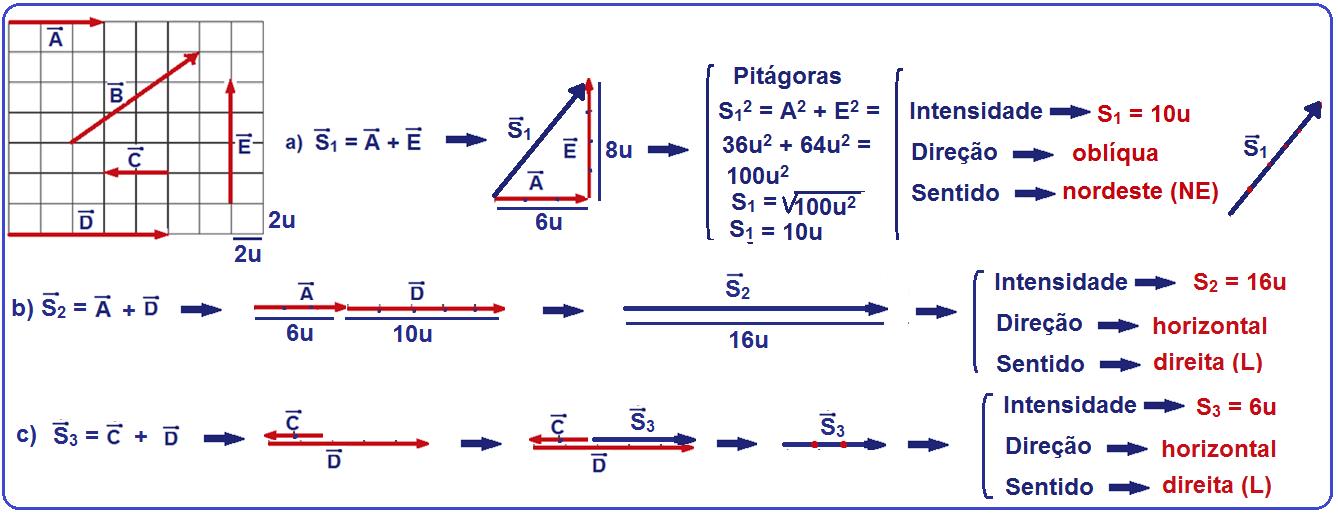
Exemplo
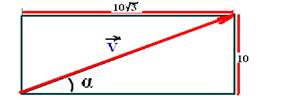
Determine
a intensidade
(no SI), direção e sentido do vetor ![]() da
figura abaixo.
da
figura abaixo.
![]()

Dois ou mais vetores são iguais quando têm ao mesmo tempo mesma intensidade, mesma direção e mesmo sentido.

Adição de vetores
Pode-se determinar o vetor soma ou vetor resultante de dois ou mais vetores através de dois processos:
Método da linha poligonal
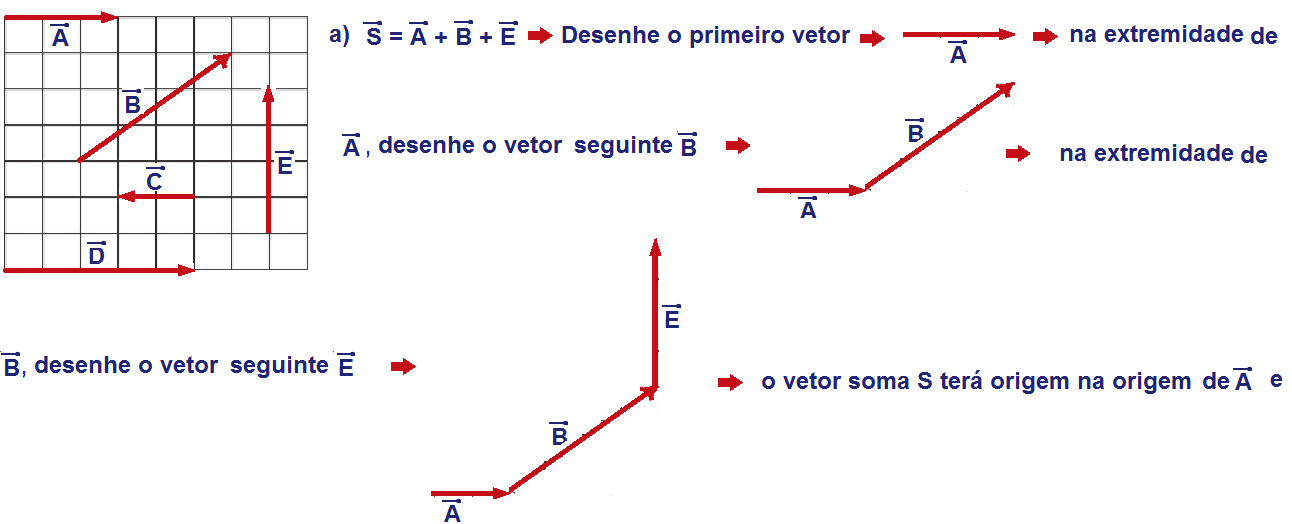
Dados
os vetores
abaixo,
determine o vetor
soma (vetor resultante) ![]() pelo
método
da linha poligonal:
pelo
método
da linha poligonal:
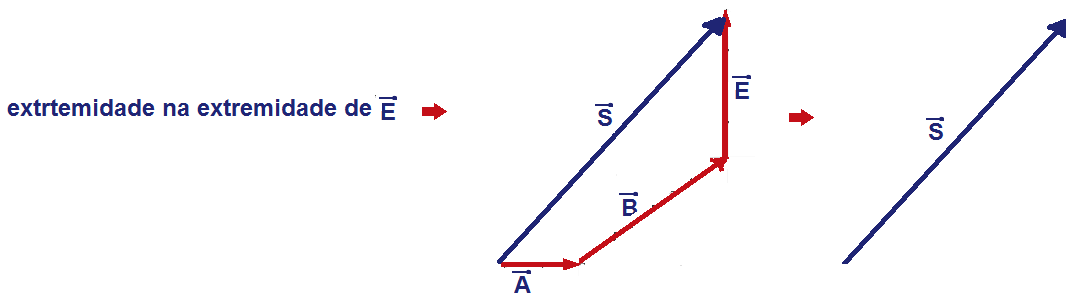
Esse
método
é
mais utilizado
quando se está interessado
apenas
na orientação
(direção e sentido)
do vetor
soma (resultante) ![]() .
.
![]() Dados os vetores
abaixo,
determine o vetor
soma (vetor resultante)
pelo
método da linha
poligonal:
Dados os vetores
abaixo,
determine o vetor
soma (vetor resultante)
pelo
método da linha
poligonal:
Se, na adição
de vetores,
a extremidade
do último
coincidir
com a origem
do primeiro,
o resultado é um vetor
nulo (![]() ).
).
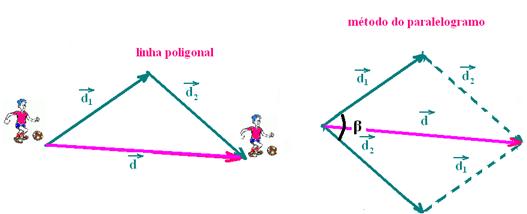
Método do paralelogramo
![]() Explicando
com um exemplo:
Explicando
com um exemplo:
Dados
os vetores
abaixo,
determine o vetor
soma (resultante) ![]() pelo
método do paralelogramo.
pelo
método do paralelogramo.
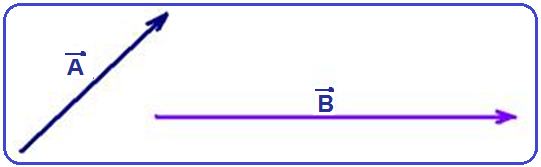
Coloque a origem dos dois vetores em um mesmo ponto e, em seguida, trace pelas extremidades de cada um deles, uma paralela ao outro, com linha pontilhada.

Unindo
os pontos indicados
e colocando a seta
conforme a figura acima,
você obterá o vetor![]() que é o vetor soma ou o vetor resultante.
que é o vetor soma ou o vetor resultante.
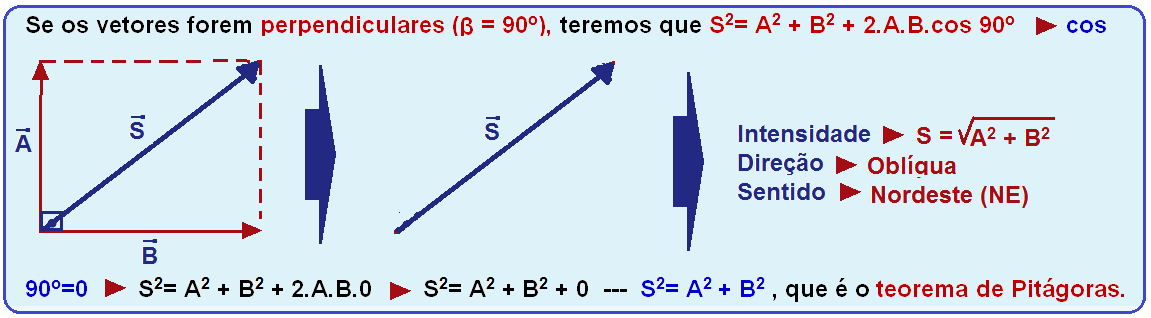
Sendo
β
o ângulo entre
os dois vetores,
pode-se determinar o módulo
ou intensidade do vetor
![]() pela lei dos cossenos:
pela lei dos cossenos:


Subtração de vetores
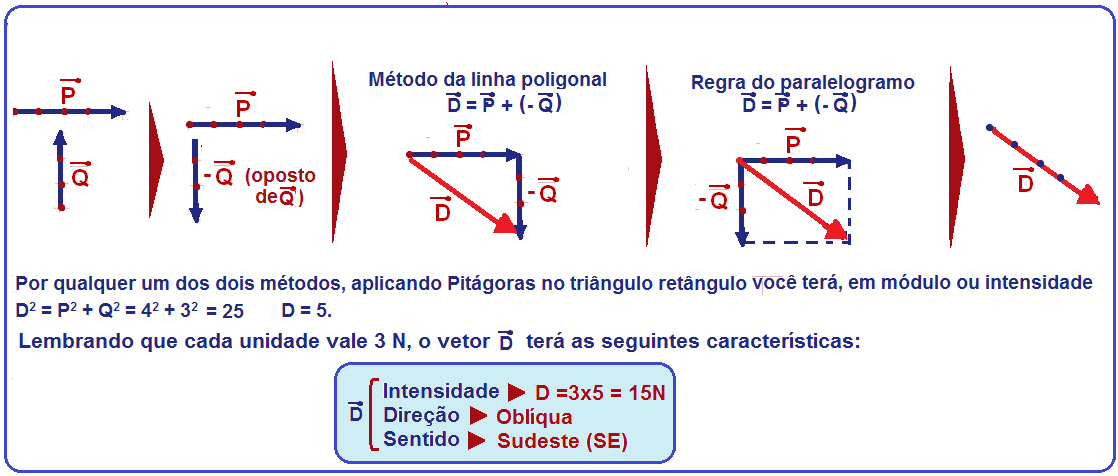
Dois vetores são opostos quando têm a mesma intensidade, mesma direção, mas sentidos contrários.
Subtrair um vetor é somá-lo ao oposto do outro.
![]()
![]()

Exemplos:
Dado
o vetor ![]() de
intensidade
V=3 unidades (3u),
pede-se:
de
intensidade
V=3 unidades (3u),
pede-se:


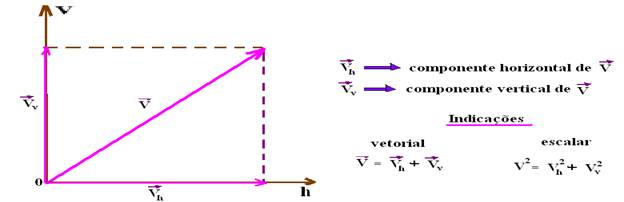
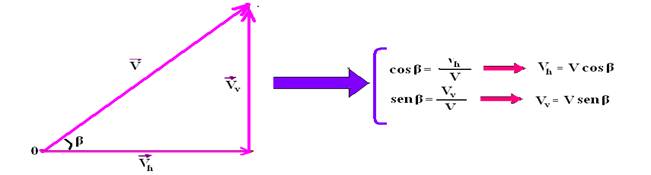
Decomposição cartesiana de um vetor
Pode-se,
a partir de um vetor ![]() ,
obter os vetores
,
obter os vetores ![]() e
e ![]() que
deram origem a ele, traçando retas paralelas aos eixos Oh e
Ov.
que
deram origem a ele, traçando retas paralelas aos eixos Oh e
Ov.
Versor
Chama-se versor qualquer vetor de módulo (intensidade) igual a 1. Qualquer vetor pode ser expresso em função de seus versores horizontais e verticais.
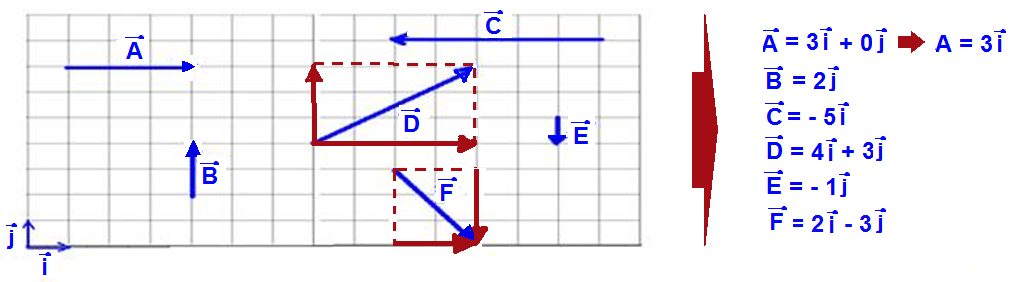
Exemplo:
Cada
divisão
da figura abaixo tem 1
unidade.
Representar
cada vetor em função de ![]() e
e ![]()
Exercícios de vestibulares sobre vetores
01-(UFB) Observe a figura a seguir e determine quais os vetores que:
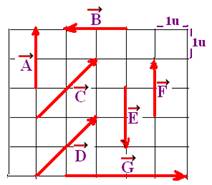
a) tem a mesma direção.
b) tem o mesmo sentido.
c) tem a mesma intensidade (módulo)
d) são iguais.
02-(UFB) Quantos sentidos possui uma direção?
03-(FGV-SP) São grandezas escalares:
a) tempo, deslocamento e força
b) força, velocidade e aceleração
c) tempo, temperatura e volume
d) temperatura, velocidade e volume
e) tempo, temperatura e deslocamento
04- (Cefet-PR) Verifique quais são as grandezas escalares e vetoriais nas afirmações abaixo.





1) O deslocamento de um avião foi de 100 km, na direção Norte do Brasil.
2) A área da residência a ser construída é de 120,00 m2.
3) A força necessária para colocar uma caixa de 10 kg em uma prateleira é de 100 N.
4) A velocidade marcada no velocímetro de um automóvel é de 80 km/h.
5) Um jogo de futebol tem um tempo de duração de 90 minutos.
Assinale a alternativa que apresenta a seqüência correta.
a) vetorial, vetorial, escalar, vetorial, escalar. b) vetorial, escalar, escalar, vetorial, escalar.
c) escalar, escalar, vetorial, vetorial, escalar. d) vetorial, escalar, vetorial, vetorial, escalar.
e) escalar, escalar, vetorial, escalar, escalar.
05-(UEPG-PR) Quando dizemos que a velocidade de uma bola é de 20m/s, horizontal e para a direita,

estamos definindo a velocidade como uma grandeza:
![]()
06-(UESC-BA) Desprezando-se a força de resistência do ar, a aceleração de queda de um corpo nas proximidades da superfície terrestre é, aproximadamente, igual a 10m/s2.
Nessas condições, um corpo que cai durante 3 segundos, a partir do repouso, atinge o solo com velocidade igual a v, após percorrer, no ar, uma distância h.
a) Das grandezas físicas citadas, têm natureza vetorial:
a) aceleração, velocidade e força;
b) força, aceleração e tempo;
c) tempo, velocidade e distância;
d) distância, tempo e aceleração;
e) velocidade, força e distância.
Exercícios de vestibulares sobre adição de vetores
07-(UFMG) Uma pessoa sai para dar um passeio pela cidade, fazendo o seguinte percurso: sai de casa e anda 2 quarteirões para o Norte; dobra à esquerda andando mais 2 quarteirões para Oeste, virando, a seguir, novamente à esquerda e andando mais dois quarteirões para o Sul. Sabendo que cada quarteirão mede 100m, o deslocamento da pessoa é:
a) 700m para Sudeste
b) 200m para Oeste
c) 200m para Norte
d) 700m em direções variadas
e) 0m
08-(UFC-CE) Analisando a disposição dos vetores BA, EA, CB, CD e DE, conforme figura a seguir, assinale a alternativa que contém a relação vetorial correta.
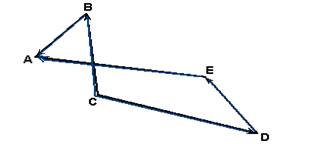
a) CB + CD + DE = BA + EA
b) BA + EA + CB = DE + CD
c) EA - DE + CB = BA + CD
d) EA - CB + DE = BA – CD
e) BA - DE - CB = EA + CD
09-(PUC-RJ) Os ponteiros de hora e minuto de um relógio suíço têm, respectivamente, 1 cm e 2 cm. Supondo que cada ponteiro do relógio é um vetor que sai do centro do relógio e aponta na direção dos números na extremidade do relógio, determine o vetor resultante da soma dos dois vetores correspondentes aos ponteiros de hora e minuto quando o relógio marca 6 horas.
a) O vetor tem módulo 1 cm e aponta na direção do número 12 do relógio.
b) O vetor tem módulo 2 cm e aponta na direção do número 12 do relógio.
c) O vetor tem módulo 1 cm e aponta na direção do número 6 do relógio.
d) O vetor tem módulo 2 cm e aponta na direção do número 6 do relógio.
e) O vetor tem módulo 1,5 cm e aponta na direção do número 6 do relógio.
10-(CFT-CE) Para se posicionar frente ao gol adversário, um jogador efetua deslocamentos rápidos e

sucessivos em linha reta,com módulos de 1,8 m e 2,4 m, deixando completamente para trás a defesa oponente. Para que o deslocamento resultante da bola seja de 3,0m, o ângulo entre estes deslocamentos deve ser de:
a) 0° b) 30° c) 60° d) 90° e) 120°
11-(CFT-CE) Dados os vetores "a", "b", "c", "d" e "e" a seguir representados, obtenha o módulo do vetor soma:
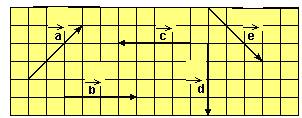
![]()
a) zero b) √20 c) 1 d) 2 e) √52
12- (PUC- SP) Os esquemas ao lado mostram um barco retirado de um rio por dois homens. Em (a) são usadas cordas que transmitem ao barco forças paralelas de intensidades F1 e F2. Em (b) são usadas cordas inclinadas de 90º que transmitem ao barco forças de intensidades iguais às anteriores.
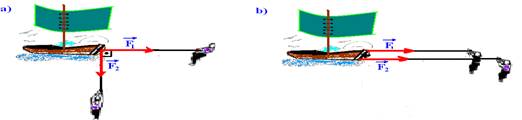
Sabe-se que, no caso (a), a força resultante transmitida ao barco tem intensidade 50kgf e que, no caso (b), tem intensidade de 70kgf. Nessas condições, determine os esforços desenvolvidos pelos dois homens.
13-(FATEC-SP) Um automóvel percorre 6,0km para o norte e, em seguida 8,0km para o leste. A intensidade do vetor posição, em relação ao ponto de partida é:
![]()
14-(INATEL- MG) - João caminha 3 metros para oeste e depois 6 metros para o sul. Em seguida, caminha 11 metros para leste. Em relação ao ponto de partida, podemos afirmar que João está:
a) a 10 m para sudeste;
b) a 10 m para sudoeste;
c) a 14 m para sudeste;
d) a 14 m para sudoeste;
e) a 20 m para sudoeste.
15-(UEL-PR)
Na figura a seguir estão desenhados dois vetores (![]() e
e![]() ).
Esses vetores representam deslocamentos sucessivos de um corpo. Qual
é o módulo do vetor igual a
).
Esses vetores representam deslocamentos sucessivos de um corpo. Qual
é o módulo do vetor igual a ![]() +
+![]() ?
?
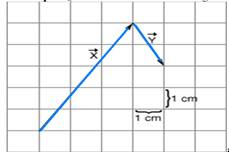
![]()
16-(MACKENZIE-SP) Com seis vetores de módulo iguais a 8u, construiu-se o hexágono regular abaixo. O módulo do vetor resultante desses seis vetores é:
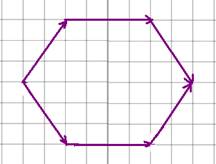
![]()
17-(URCAMP-RS) No sistema plano figurado, representamos os vetores R iguais em módulo. Calcule
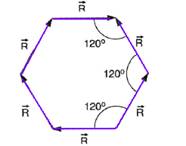
a intensidade do vetor soma.
18-(FCC-SP)
Qual é a relação entre os vetores, ![]() ,
,![]() ,
,![]() ,
e
,
e ![]() representados
abaixo?
representados
abaixo?
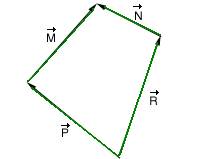
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) ![]() .
.
e) ![]() .
.
19-(UnB-DF) Sobre a composição dos vetores a seguir podemos dizer que:
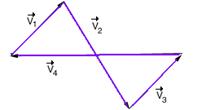
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) ![]() .
.
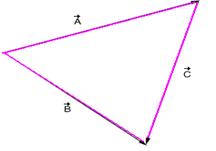
20-(UnB-DF) É dado o diagrama vetorial da figura. Qual a expressão correta?
a) ![]() .
.
b) ![]() .
.
c) ![]() .
.
d) ![]() .
.
e) ![]() .
.
21-(UnB-DF) Considere um relógio com mostrador circular de 10 cm de raio e cujo ponteiro dos minutos tem comprimento igual ao raio do mostrador. Considere esse ponteiro como um vetor de origem no centro do relógio e direção variável. O módulo da soma dos três vetores determinados pela posição desse ponteiro quando o relógio marca exatamente 12 horas, 12 horas e 20 minutos e, por fim, 12 horas e 40 minutos é, em cm, igual a:
a) 30.
b) ![]() .
.
c) 20.
d) zero.
22-(UNEB-BA) Um jogador de golfe necessita de quatro tacadas para colocar a bola no buraco. Os quatro deslocamentos estão representados na figura abaixo.

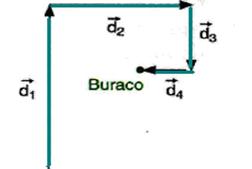
Sendo d1 = 15 m, d2 = 6,0 m, d3 = 3,0 m e d4 = 1,0 m, a distância inicial da bola ao buraco era, em metros, igual a:
![]()
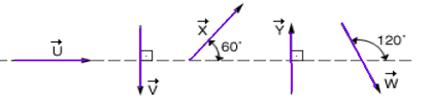
23-(UEL-PR)
Dados os vetores ![]() ,
, ![]() ,
, ![]() ,
, ![]() e
e ![]() de
mesmo módulo, qual das relações abaixo está correta?
de
mesmo módulo, qual das relações abaixo está correta?
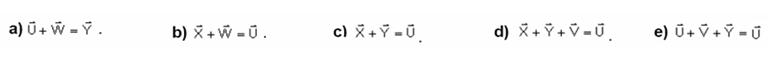
24-(UFRN) - A figura abaixo representa os deslocamentos de um móvel em várias etapas.
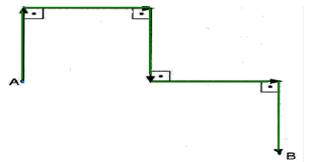
Cada vetor tem módulo igual a 20 m. A distância percorrida pelo móvel e o módulo do vetor deslocamento são, respectivamente:
a) 20√5m e 20√5m b) 40 m e 40√5m c) 100 m e 20√5m d) 20√5m e 40 m e) 100 m e 40√5m
25-(UCSal-BA) Dado o conjunto de vetores, marque V para as questões verdadeiras e F para as falsas.
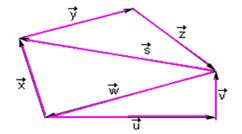
![]()
26- (Fatec-SP)
Sobre o corpo C atuam duas forças ![]() e
e ![]() ,
conforme esquema. O diagrama que fornece a resultante
,
conforme esquema. O diagrama que fornece a resultante ![]() é:
é:

27-(Ufc-CE) Na figura a seguir, onde o reticulado forma quadrados de lado L=0,50cm, estão desenhados dez vetores, contidos no plano xy. O módulo da soma de todos esses vetores é, em centímetros:
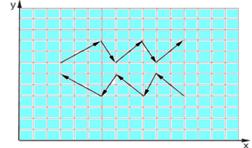
![]()
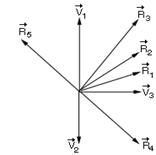
28-(MACKENZIE-SP)
A resultante dos vetores ![]() mostrados
na figura é:
mostrados
na figura é:
![]()
29-(UNIUBE-MG) Qual é o módulo da resultante da soma dos vetores representados abaixo?
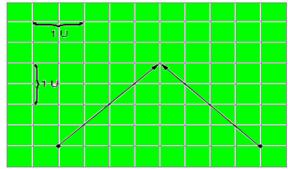
a) 2,0u
b) 3,5u
c) 4,0u
d) 7,0u
e) 8,0u
30-(PUC-BA)
Nas figuras seguintes estão representados pares de vetores ![]() e
e ![]() nos
quais cada segmento orientado está subdividido em segmentos
unitários.
nos
quais cada segmento orientado está subdividido em segmentos
unitários.
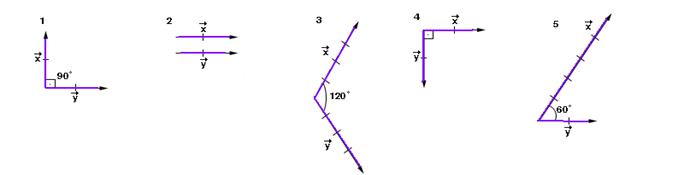
Quais destes pares têm a mesma resultante?
31-(UNESP-SP)
A figura mostra, em escala, duas forças ![]() e
e ![]() ,
atuando num mesmo ponto material P.
,
atuando num mesmo ponto material P.
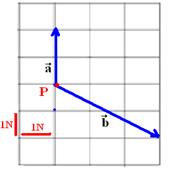
a)
Represente na figura reproduzida a força ![]() ,
resultante das forças
,
resultante das forças ![]() e
e ![]() ,
e determine o valor de seu módulo , em newtons.
,
e determine o valor de seu módulo , em newtons.
b)
Represente, também na mesma figura, a força ![]() ,
de tal modo que
,
de tal modo que ![]() .
.
32-(FATEC-SP) Duas forças têm intensidades F1=10N e F2=15N. O módulo da resultante da soma vetorial desses dois vetores, não pode ser:
![]()
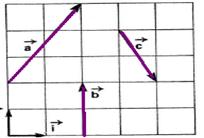
33-(FATEC-SP)
No gráfico anexo estão representados três vetores ![]() .
Os vetores
.
Os vetores ![]() e
e ![]() são
unitários. Analise as informações:
são
unitários. Analise as informações:

34-(PUC-RJ) Um veleiro deixa o porto navegando 70 km em direção leste.

Em seguida, para atingir seu destino, navega mais 100 km na direção nordeste. Desprezando a curvatura da terra admitindo que todos os deslocamentos são coplanares, determine o deslocamento total do veleiro em relação ao porto de origem.
(Considere √2 = 1,40 e √5 = 2,20)
a) 106 km
b) 34 km
c) 154 km
d) 284 km
e) 217 km
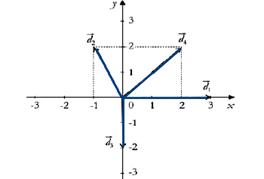
35-(UFPB-PB)
Uma bola de bilhar sofre quatro deslocamentos sucessivos
representados pelos vetores ![]() apresentados
no diagrama abaixo.
apresentados
no diagrama abaixo.
![]()
36-(UFAL-AL) A localização de um lago, em relação a uma caverna pré-histórica, exigia que se

caminhasse 200 m numa certa direção e, a seguir, 480 m numa direção perpendicular à primeira. A distância em linha reta, da caverna ao lago era, em metros,
a) 680
b) 600
c) 540
d) 520
e) 500
37-(UFPB-PB)
Considere os vetores![]() ,
, ![]() e
e ![]() ,
nos diagramas numerados de I a IV.
,
nos diagramas numerados de I a IV.

Os
diagramas que, corretamente, representam a relação
vetorial ![]() =
= ![]() -
- ![]() são
apenas:
são
apenas:
a) I e III
b) II e IV
c) II e III
d) III e IV
e) I e IV
38-(UEG-GO)
Considerando que os vetores ![]() ,
, ![]() e
e ![]() satisfazem
à equação vetorial
satisfazem
à equação vetorial ![]() +
+ ![]() =
=![]() e
seus módulos estão relacionados pela equação escalar A + B = C,
responda ao que se pede.
e
seus módulos estão relacionados pela equação escalar A + B = C,
responda ao que se pede.
a) Como está orientado o vetor A em relação ao vetor B? Justifique o seu raciocínio.
b) Considere agora que a relação entre os seus módulos seja dada por A2 + B2 = C2.
Qual seria a nova orientação do vetor B em relação ao vetor A? Justifique seu raciocínio.
39- (FUVEST-SP) Um viajante saiu de Araripe, no Ceará, percorreu, inicialmente, 1.000 km para o
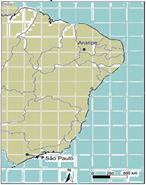
sul, depois 1.000 km para o oeste e, por fim, mais 750 km para o sul. Com base nesse trajeto e no mapa acima, pode-se afirmar que, durante seu percurso, o viajante passou pelos estados do Ceará,
a) Rio Grande do Norte, Bahia, Minas Gerais, Goiás e Rio de Janeiro, tendo visitado os ecossistemas da Caatinga, Mata Atlântica e Pantanal. Encerrou sua viagem a cerca de 250 km da cidade de São Paulo.
b) Rio Grande do Norte, Bahia, Minas Gerais, Goiás e Rio de Janeiro, tendo visitado os ecossistemas da Caatinga, Mata Atlântica e Cerrado. Encerrou sua viagem a cerca de 750 km da cidade de São Paulo.
c) Pernambuco, Bahia, Minas Gerais, Goiás e São Paulo, tendo visitado os ecossistemas da Caatinga, Mata Atlântica e Pantanal. Encerrou sua viagem a cerca de 250 km da cidade de São Paulo.
d) Pernambuco, Bahia, Minas Gerais, Goiás e São Paulo, tendo visitado os ecossistemas da Caatinga, Mata Atlântica e Cerrado. Encerrou sua viagem a cerca de 750 km da cidade de São Paulo.
e) Pernambuco, Bahia, Minas Gerais, Goiás e São Paulo, tendo visitado os ecossistemas da Caatinga, Mata Atlântica e Cerrado. Encerrou sua viagem a cerca de 250 km da cidade de São Paulo.
Instrução: As questões 40 e 41 devem ser respondidas com base na situação física descrita a seguir.

No esquema apresentado na figura abaixo, uma partícula de poeira cósmica, cuja massa é igual a 2,0 g, move-se livremente de norte para o sul, com velocidade de módulo igual a 1,2 km/s. No instante visualizado nesse esquema (t = 0), passam a atuar sobre essa partícula as forças A, B e C nele representadas, sendo todas elas constantes.
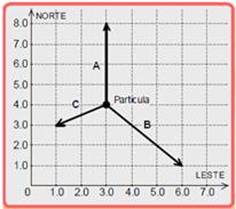
Considere também que os valores numéricos associados aos eixos “norte” e “leste” referem-se à unidade de força do Sistema Internacional: newton (N).
40-(IFNMG-MG)

O módulo da velocidade da partícula no instante t = 1,0 s, expresso em km/s, está corretamente apresentado na alternativa:
A) 1,3
B) 2,4
C) 1,0
D) 1,8
41-(IFNMG-MG)

No instante t = 1,0 s, as forças A, B e C deixam de atuar na partícula. Nessas condições, a forma da trajetória da partícula, desde t = 0, está corretamente descrita na alternativa:
A) Retilínea, desde t = 0, e ainda retilínea, após t = 1,0 s.
B) Inicialmente circular e, após 1,0 s, retilínea.
C) Inicialmente circular e, após 1,0 s, parabólica.
D) Inicialmente parabólica e, após t = 1,0 s, retilínea.
42-(AFA)
Os vetores ![]() ,
na figura abaixo, representam, respectivamente, a velocidade do vento
medida em relação ao solo e a
,
na figura abaixo, representam, respectivamente, a velocidade do vento
medida em relação ao solo e a

velocidade de um avião em pleno vôo, medida em relação ao vento.
Sabendo-se
que o movimento resultante do avião acontece em uma direção
perpendicular à direção da velocidade do vento, tem-se que o
cosseno do ângulo θ entre os vetores velocidades ![]() ,
em módulo, vale
,
em módulo, vale
a) B/A
b) A/B
c) – A/B
d) – A.B
Resolução comentada dos exercícios sobre vetores
01- a)
![]() ---
--- ![]() ---
--- ![]()
b) ![]()
c) ![]()
d) ![]()
![]()
02- Dois
03- R- B --- são perfeitamente definidas por um número acrescido de uma unidade.
04- 1) deslocamento --- vetorial --- 2) área --- escalar --- 3) força --- vetorial --- 4) velocidade --- vetorial --- 5) tempo --- escalar --- R- E
05- R- D
06- A
07-
Soma
vetorial --- ![]()
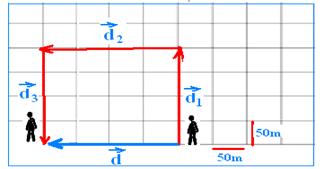
R- B
08- CD + DE + EA = CB + BA --- EA – CB +DE = BA – CD --- R- D
09- Somando os vetores pelo método da linha poligonal
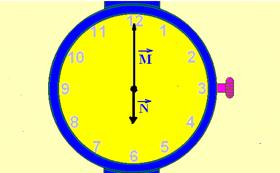

R- A
10-
Lei dos cossenos --- d2=d12 + d22 + 2.d1.d2.cosβ --- 9=3,24 + 5,76 + 8,64cosβ --- 9 – 9=8,64 cosβ --- cosβ=0 --- β=90o --- R- D
11-
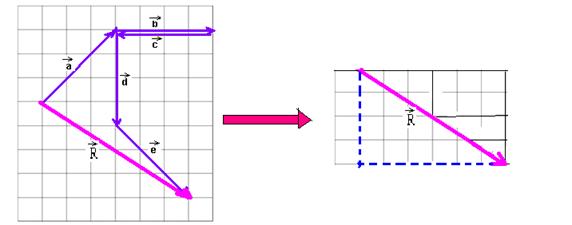
R2=42 + 62 --- R=√52 --- R- E
12- a)
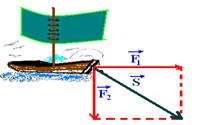
S2=F12 + F22 --- 502=F12 + F22 --- 2.500=F12 + F22 I
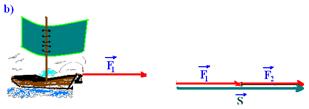
S=F1 + F2 --- 70=F1 + F2 --- F1=70 – F2 II --- II em I --- 2.500=(70 – F2)2 --- 2.500=4.900 – 140F2 + F22 + F2=2 --- 2F22 – 140F2 + 2.400=0 --- F22 – 70F2 + 1.200=0 --- F2=(70±10)/2 --- F2=30kgf e F1=40kgf --- ou --- F2=40kgf e F1=30kgf
13-
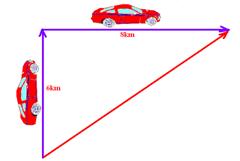
Pitágoras --- R- D
14- Na
figura abaixo está a soma dos três vetores e, para calcular o
módulo de ![]() ,
aplica-se Pitágoras no triângulo hachurado.
,
aplica-se Pitágoras no triângulo hachurado.
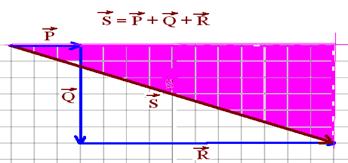
S2=142 + 62 --- S=15,2m --- R- C
15- Aplicando Pitágoras no triângulo hachurado
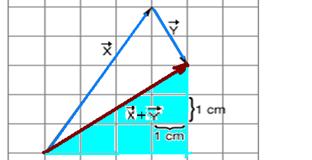
![]() +
+![]() =5
--- R-
B
=5
--- R-
B
16- Dividindo o hexágono conforme a figura abaixo e calculando o vetor soma (resultante) pelo método da linha poligonal em cima e
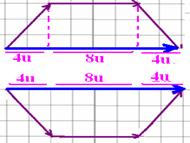
em baixo, o vetor soma dos dois vetores de módulo 16u será 16u + 16u=32u --- R- B
17- Dividindo o hexágono e calculando o módulo de M
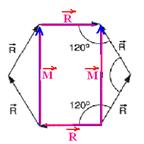

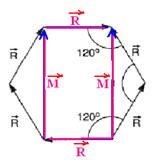
Observe
na figura acima que os vetores ![]() de
cima e de baixo se anulam e o vetor soma terá intensidade
S=2M=2.3.√R --- S=6√R
de
cima e de baixo se anulam e o vetor soma terá intensidade
S=2M=2.3.√R --- S=6√R
18- Usando o método da linha poligonal
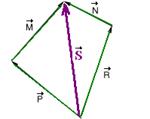
R- B
19-
![]() --- R-
C
--- R-
C
20- ![]() --- R-
D
--- R-
D
21-
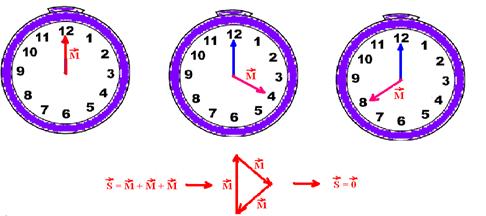
R- D
22- Calculando S e aplicando Pitágoras no triângulo hachurado
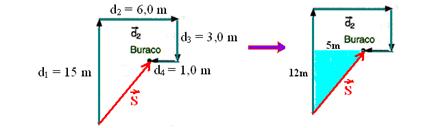
S2 = 122 + 52 --- S=13m --- R- C
23-

R- E
24- A distância percorrida ΔS (indicação do odômetro do carro) é fornecida pela soma algébrica de todos os deslocamentos --- ΔS=5.20=100m --- unindo A com B obtém-se o vetor deslocamento que é calculado aplicando-se Pitágoras no triângulo
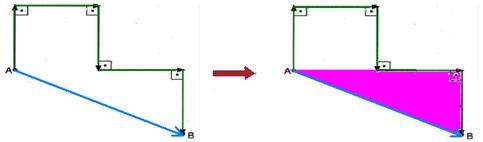
hachurado --- d=402 + 202 --- d=√2.000 --- d=20√5m --- R- C
25- a) Falsa b) Verdadeira c) verdadeira d) falsa e) falsa f) verdadeira
26- R- D
27- Somando todos os vetores pelo método da linha poligonal
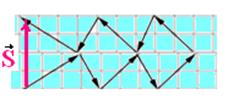
S=4.0,50=2.0cm --- R- E
28-
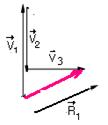
R- A
29-
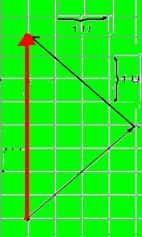
R- C
30-

R- 2 e 3
31- a)
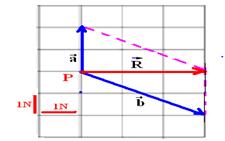
Módulo --- R=3N
b) Após a soma, a origem (P) tem que coincidir com a extremidade (P)

32- Como não foi especificado a direção e o sentido desses dois vetores, eles podem ser quaisquer --- valor máximo de R=10 + 15=25N (mesma direção e mesmo sentido) --- valor mínimo de R=15 – 10=5N (mesma direção e sentidos contrários) --- portanto R não pode ser superior a 25N, nem inferior a 5N --- R- A
33- Observe a figura abaixo onde os vetores foram decompostos
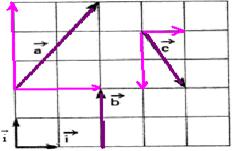
R- C
34- Nas condições do exercício --- α=45o --- lei dos cossenos --- R2 = 702 + 1002 + 2.70.100.cosα --- R2 = 4.900 + 10.000 + 14.000.√2/2 --- R=157,2km --- R- C
35-
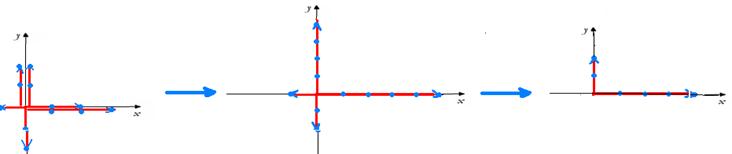
R- D
36-- A figura mostra os deslocamentos citados e a distância procurada.
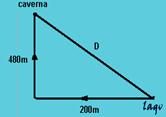
Como
o triângulo mostrado é retângulo é só aplicarmos o teorema de
Pitágoras --- ![]()
R- D
37-
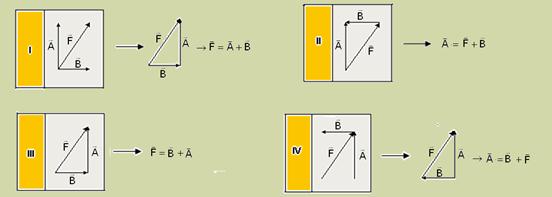
R- B
38- a) O vetor A está orientado na mesma direção e sentido do vetor B, ou seja, os vetores A e B são paralelos. Quando os vetores
![]()
se
encontram na mesma direção e sentido (neste exemplo, horizontal) e
o módulo do vetor resultante (![]() )
é obtido somando-se os seus módulos, ou seja, C = A + B.
)
é obtido somando-se os seus módulos, ou seja, C = A + B.
b)
O vetor ![]() está
orientado em uma direção perpendicular ao vetor
está
orientado em uma direção perpendicular ao vetor ![]() .
Quando os vetores são perpendiculares, a soma dos
.
Quando os vetores são perpendiculares, a soma dos

quadrados dos seus módulos é igual ao quadrado do módulo do vetor resultante, ou seja, C2 = A2 + B2.
39- A escala gráfica dispõe que cada centímetro do mapa equivale a 250 quilômetros do terreno, o que facilita representar
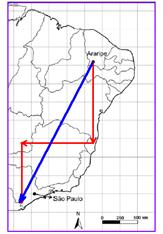
vetorialmente o percurso feito pelo viajante e, inclusive representar seu deslocamento vetorial (em azul). Dessa forma ele caminhou 1000 km para o Sul (direção fácil de identificar, pois o Norte está indicado no mapa), saindo do Ceará e passando por Pernambuco e Bahia. Nesse estado mudou de rumo e viajou 1.000 km para o Oeste, chegando a Goiás, a partir de onde rumou mais 750 km para o Sul, chegando ao estado de São Paulo. Nesse trajeto o viajante avistou os ecossistemas da Caatinga, do Cerrado e da Mata Atlântica.
R- E
40-
Para calcular a intensidade da força resultante que age sobre a partícula cósmica você pode decompor as forças nas direções norte e leste --- observe na sequência abaixo que a intensidade da força resultante é de 1N no sentido leste ---
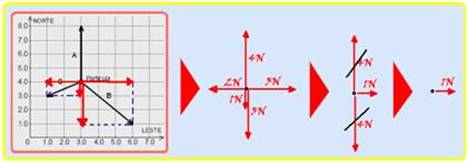
Como a velocidade inicial da partícula tem intensidade Vo=1200m/s do norte para o sul e a força resultante sobre ela tem intensidade 1N do oeste para leste, o movimento da partícula tem as características de composição de dois movimentos, um no sentido leste e outro no sentido sul (veja figura) --- no sentido leste, a projeção da velocidade inicial é nula VoL=0 e ela se desloca sob ação de uma força resultante de valor FR=1N e com aceleração --- FR=m.a --- 1=2.10-3.a --- a= 500m/s2 --- sua velocidade nessa direção após t=1s terá intensidade --- VL=VoL + aL.t=0 + 500.1 --- VL=500m/s --- no sentido sul ela será lançada para baixo com VoS=1200m/s, acelerando com aceleração da gravidade g=10m/s2 --- após t=1s, sua velocidade nessa direção será --- VS=VoS + g.t=1200 + 10.1=1210m/s ---
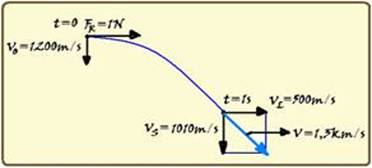
observe na figura que essas duas velocidades são perpendiculares e, aplicando Pitágoras você obterá V2 = VL2 + VS2=(500)2 + (1210)2 --- V=√(1714100) --- V=1309m/s=1,3km/s --- R- A.
41- Pelo princípio da inércia, se as forças deixarem de atura, a força resultante sobre ela será nula e, após esse innstante, por inércia, ela seguirá em MRU com velocidade constante de 1,3km/s --- observe na resolução do exercício anterior (08) que, antes de 1s a trajetória era parabólica --- R- D.
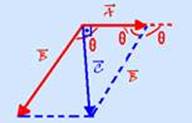
42- A
soma vetorial de ![]() com
com ![]() fornece
a velocidade
fornece
a velocidade ![]() do
avião em relação ao solo --- observe na figura
que θ +
do
avião em relação ao solo --- observe na figura
que θ +
θ’=180o ---cosθ’=cos(180 – θ)= - cos θ --- - cosθ=cateto adjacente/hipotenusa=A/B --- cosθ= - A/B --- R- C