Vestibulares Recentes - 2017 – 2016 – 2015

Termologia – (Física Térmica)

Propagação do calor

01-(UFJF-MG-017)

02-(ENEM-MEC-016)

Num experimento, um professor deixa duas bandejas de mesma massa, uma de plástico e outra de alumínio, sobre a mesa do laboratório.

Após algumas horas, ele pede aos alunos que avaliem a temperatura das duas bandejas, usando para isso o tato.

Seus alunos afirmam, categoricamente, que a bandeja de alumínio encontra-se numa temperatura mais baixa.

Intrigado, ele propõe uma segunda atividade, em que coloca um cubo de gelo sobre cada uma das bandejas, que estão em equilíbrio térmico com o ambiente, e os questiona em qual delas a taxa de derretimento do gelo será maior.

O aluno que responder corretamente ao questionamento do professor dirá que o derretimento ocorrerá

a) mais rapidamente na bandeja de alumínio, pois ela tem maior condutividade térmica do que a de plástico.

b) mais rapidamente na bandeja de plástico, pois ela tem inicialmente uma temperatura mais alta que a de alumínio.

c) mais rapidamente na bandeja de plástico, pois ela tem maior capacidade térmica do que a de alumínio.

d) mais rapidamente na de alumínio, pois ela tem calor específico menor que a de plástico.

e) com a mesma rapidez nas duas bandejas, pois apresentarão a mesma variação de temperatura.

Termologia

Conceitos iniciais

03-(COLÉGIO NAVAL – 2016/17)

Com relação à termologia, coloque V (verdadeiro) ou F (falso) e, a seguir, assinale a opção correta.

( ) Temperatura grandeza física que representa a medida do estado de agitação médio das moléculas de um corpo.

( ) Calor – energia térmica que passa, de forma espontânea, do corpo de menor temperatura para o de maior temperatura.

( ) Fusão mudança de estado físico sofrida por um líquido ao doar uma certa quantidade de calor.

( ) Evaporação passagem do estado líquido para o estado gasoso que ocorre de forma lenta.

( ) Equilíbrio térmico - condição física na qual as trocas de calor entre dois ou mais corpos deixam de existir.

( ) Convecção processo de transmissão de calor que ocorre devido à movimentação de massas, em especial, nos líquidos e nos gases.

( ) Caloria quantidade de calor necessária para que 1g de qualquer substância tenha sua temperatura alterada em 1°C .

a) (V) (V) (V) (F) (F) (V) (F)

b) (F) (F) (V) (V) (F) (F) (V)

c) (F) (F) (F) (V) (F) (V) (V)

d) (V) (F) (F) (V) (V) (V) (F)

e) (V) (V) (F) (F) (V) (F) (F)

04-(UNICAMP-SP-016)

Um isolamento térmico eficiente é um constante desafio a ser superado para que o homem possa viver em condições extremas de temperatura.

Para isso, o entendimento completo dos mecanismos de troca de calor é imprescindível.

Em cada uma das situações descritas a seguir, você deve reconhecer o processo de troca de calor envolvido.

I. As prateleiras de uma geladeira doméstica são grades vazadas, para facilitar fluxo de energia térmica até o congelador por […]

II. O único processo de troca de calor que pode ocorrer no vácuo é por […].

III. Em uma garrafa térmica, é mantido vácuo entre as paredes duplas de vidro para evitar que o calor saia ou entre por [….].

Na ordem, os processos de troca de calor utilizados para preencher as lacunas corretamente são:

a) condução, convecção e radiação.

b) condução, radiação e convecção.

c) convecção, condução e radiação.

d) convecção, radiação e condução.

Termometria

05-(FDSBC-SP-017)

Um termômetro graduado na escala J de temperaturas, quando em equilíbrio térmico com um líquido contido num recipiente, cuja temperatura é de 20^o C, marca 7^o J.

Esse termômetro quando em equilíbrio térmico com o líquido de outro recipiente, cuja temperatura é de 140^o F, passa a marcar 11^o J.

Com base nessas informações, podemos afirmar que a equação termométrica que relaciona a escala Celsius de temperaturas (T_Celsius ) com a escala J de temperaturas (T_J ) é

Calorimetria

Calor sensível (específico) e trocas de calor sem mudança de estado

06-(UNESP-SP-017)

(A) 21,6 ºC.

(B) 33,2 ºC.

(C) 45,2 ºC.

(D) 63,2 ºC.

(E) 52,0 ºC.

07-(FUVEST-SP-017)

08-(UNESP-SP-015)

A energia contida nos alimentos

Para determinar o valor energético de um alimento, podemos queimar certa quantidade desse produto e, com o calor liberado, aquecer determinada massa de água. Em seguida, mede-se a variação de temperatura sofrida pela água depois que todo o produto foi queimado, e determina-se a quantidade de energia liberada na queima do alimento. Essa é a energia que tal alimento nos fornece se for ingerido.

No rótulo de um pacote de castanha-de-caju, está impressa a tabela a seguir, com informações nutricionais sobre o produto.

Considere que 150 g de castanha tenham sido queimados e que determinada massa m de água, submetida à chama dessa combustão, tenha sido aquecida de 15 ºC para 87 ºC.

Sabendo que o calor específico da água líquida é igual a 1 cal/(gºC) e que apenas 60% da energia liberada na combustão tenha efetivamente sido utilizada para aquecer a água, é correto afirmar que a massa m, em gramas, de água aquecida era igual a

Calor Latente – trocas de calor com mudança de estado

09-(PUC-RJ/017)

Em uma experiência de física, um aluno verifica que o calor de fusão de um dado objeto é 50 J/kg.

Para outro objeto com o dobro da massa, mas feito do mesmo material, o calor de fusão, em J/kg, deve ser

10-ENEM-MEC-015)

As altas temperaturas de combustão e o atrito entre suas peças móveis são alguns dos fatores que provocam o aquecimento dos motores à combustão interna.

Para evitar o superaquecimento e consequentes danos a esses

motores, foram desenvolvidos os atuais sistemas de refrigeração, em que um fluido arrefecedor com propriedades especiais circula pelo interior do motor, absorvendo o calor que, ao passar pelo radiador, é transferido para a atmosfera.
Qual propriedade o fluido arrefecedor deve possuir para cumprir seu objetivo com maior eficiência?
a) Alto calor específico.
b) Alto calor latente de fusão.
c) Baixa condutividade térmica.
d) Baixa temperatura de ebulição.
e) Alto coeficiente de dilatação térmica

11-(UNIFESP-SP-016)

Considere um copo de vidro de 100 g contendo 200 g de água líquida, ambos inicialmente em equilíbrio térmico a 20 ºC.

O copo e a água líquida foram aquecidos até o equilíbrio térmico a 50 ºC, em um ambiente fechado por paredes adiabáticas, com vapor de água inicialmente a 120 ºC.

A tabela apresenta valores de calores específicos e latentes das substâncias envolvidas nesse processo.

Considerando os dados da tabela, que todo o calor perdido pelo vapor tenha sido absorvido pelo copo com água líquida e que o processo tenha ocorrido ao nível do mar, calcule:

a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

12-(UFJF-MG-017)

13- (Faculdade de Medicina do Hospital Israelita Albert Einstein)

Sabe-se que um líquido possui calor específico igual a 0,58 cal/g.^oC.

Com o intuito de descobrir o valor de seu calor latente de vaporização, foi realizado um experimento onde o líquido foi aquecido por meio de uma fonte de potência uniforme, até sua total vaporização, obtendo-se o gráfico abaixo.

O valor obtido para o calor latente de vaporização do líquido, em cal/g, está mais próximo de:

14-(FMJ-SP-017)

Para se elevar a temperatura de certa massa de água de 20°C para 100°C, foram necessárias 1,6.104 cal. Sendo o calor específico da água igual a1,0 cal/g.°C e o calor latente de vaporização da água 540 cal/g, a quantidade de calor necessária apenas para vaporizar essa massa de água é

(A) 4,32 × 104 cal.

(B) 5,40 × 104 cal.

(C) 1,08 × 105 cal.

(D) 6,48 × 105 cal.

(E) 8,64 × 105 cal.

Trocas de Calor

15-(PUC-SP-017)

Uma xícara contém 30mL de café a 60 C. Qual a quantidade, em mL, de leite frio, cuja

temperatura é de 10^oC, que devemos despejar nessa xícara para obtermos uma mistura de café com leite a 40^oC? Considere as trocas de calor apenas entre o café e o leite, seus calores específicos iguais e suas densidades iguais a 1g/cm³.

(A) 15

(B) 20

(C) 25

(D) 35

16-(ENEM-MEC-015)

Uma garrafa térmica tem como função evitar a troca de calor entre o líquido nela contido e o ambiente, mantendo a temperatura de seu conteúdo constante.

Uma forma de orientar os consumidores na compra de uma garrafa térmica seria criar um selo de qualidade, como se faz atualmente para informar o consumo de energia de eletrodomésticos.

O selo identificaria cinco categorias e informaria a variação de temperatura do conteúdo da garrafa, depois de decorridas seis horas de seu fechamento, por meio de uma porcentagem do valor inicial da temperatura de equilíbrio do líquido na garrafa.
O quadro apresenta as categorias e os intervalos de variação percentual da temperatura.

Para atribuir uma categoria a um modelo de garrafa térmica, são preparadas e misturadas, em uma garrafa, duas amostras de água, uma a 10°C e outra a 40°C, na proporção de um terço de água fria para dois terços de água quente.

A garrafa é fechada. Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se 16°C.
Qual selo deveria ser posto na garrafa térmica testada?

Dilatometria

Dilatação linear, superficial e volumétrica

17-(MACKENZIE-SP-2017)

18-(AFA – 016/017)

19-(Medicina – USCS-SP-017)

20-(FGV-SP-017)

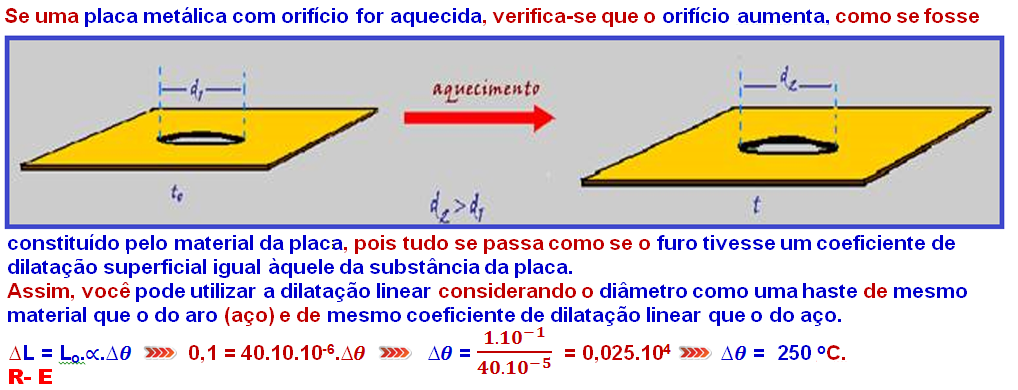
Um bloco metálico, maciço, homogêneo, de capacidade térmica C, é feito de um material de

coeficiente de dilatação linear α e ocupa um volume V_o à temperatura ambiente.

Ele é colocado no interior de um forno quente e recebe uma quantidade de calor Q até entrar em equilíbrio térmico com o forno sem sofrer mudança de estado físico.

Como consequência, seu volume sofre uma dilatação ∆V.

Tal dilatação é diretamente proporcional a V_o,

21-(AFA – 015/016)

Consultando uma tabela da dilatação térmica dos sólidos verifica-se que o coeficiente de dilatação

linear do ferro é 13.10^-6 ^oC^-1.

Portanto, pode-se concluir que

a) num dia de verão em que a temperatura variar 20 °C o comprimento de uma barra de ferro de 10,0 m sofrerá uma variação de 2,6 cm

b) o coeficiente de dilatação superficial do ferro é 169.10^-6 ^oC^-1..

c) para cada 1 °C de variação de temperatura, o comprimento de uma barra de 1,0 m desse material varia 13.10^-6m⋅

d) o coeficiente de dilatação volumétrica do ferro é 39.10^-18 ^oC^-1.

Termodinâmica

Mudanças de estado físico

22-(FGV-SP-017)

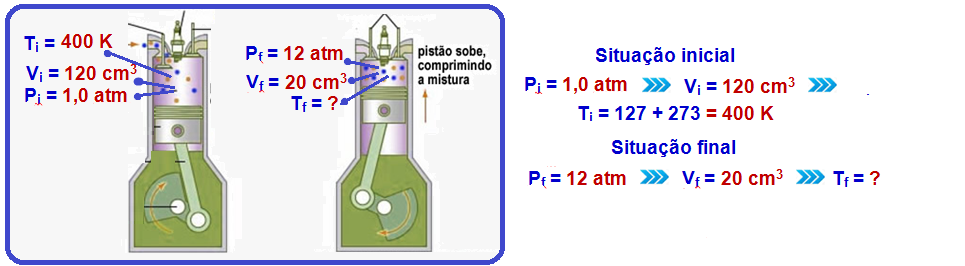
Ao ser admitido no interior da câmara de combustão do motor de uma motocicleta, o

vapor de etanol chega a ocupar o volume de 120 cm3 sob pressão de 1,0 atm e temperatura de

127 ^oC.

Após o tempo de admissão, o pistão sobe, o volume ocupado por essa mistura diminui para 20 cm³, e a pressão aumenta para 12 atm.

Considerando a mistura um gás ideal e desprezando perdas de calor devido à rápida compressão, a temperatura do gás resultante desse processo no interior da câmara passa a ser, em ^oC, de

Transformações gasosas

23- (EsPCEx- AMAN – SP- RJ – 2016/17)

Durante um experimento, um gás perfeito é comprimido, adiabaticamente,sendo realizado sobre ele um trabalho de 800 J.

Em relação ao gás, ao final do processo, podemos afirmar que:

a) o volume aumentou, a temperatura aumentou e a pressão aumentou.

b) o volume diminuiu, a temperatura diminuiu e a pressão aumentou.

c) o volume diminuiu, a temperatura aumentou e a pressão diminuiu.

d) o volume diminuiu, a temperatura aumentou e a pressão aumentou.

e) o volume aumentou, a temperatura aumentou e a pressão diminuiu.

24-(UNICAMP-SP-017)

Em seguida, a válvula A é fechada e o ar que está dentro do pistão é expulso através de uma válvula B, ligada à atmosfera, completando um ciclo de bombeamento.

Considere que o ar se comporte como um gás ideal e que, durante o ciclo completo, a temperatura não variou.

Se a pressão inicial na câmara é de P_i = 33 Pa, a pressão final na câmara após um ciclo de bombeamento será de

Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia

25-(UNESP-SP-017-Meio do ano)

A figura 1 mostra um cilindro reto de base circular provido de um pistão, que desliza sem atrito. O cilindro contém um gás ideal à temperatura de 300 K, que inicialmente ocupa um volume de 6,0 × 10-3 m³ e está a uma pressão de 2,0 × 10⁵ Pa.

O gás é aquecido, expandindo-se isobaricamente, e o êmbolo desloca-se 10 cm até atingir a posição de máximo volume, quando é travado, conforme indica a figura 2.

Considerando a área interna da base do cilindro igual a 2,0 × 10^-2 m², determine a temperatura do gás, em kelvin, na situação da figura 2.

Supondo que nesse processo a energia interna do gás aumentou de 600 J, calcule a quantidade de calor, em joules, recebida pelo gás. Apresente os cálculos.

26-(UFES – ES – 017)

27-(PUC-SP-017)

Um gás monoatômico submetido a uma pressão de 1 atm possui volume de 1000 cm3 quando sua temperatura é de 300 K.

Após sofrer uma expansão isobárica, seu volume é aumentado para 300% do valor inicial. Determine a variação da energia interna do gás e o trabalho mecânico, em joules, realizado pelo gás durante essa transformação.

(A) 2.102 e 3.102

(B) 2.108 e 2.108

(C) 3.104 e 2.104

(D) 3.102 e 2.102

28-(UNIFESP-SP-017)

Uma massa constante de gás ideal pode ser levada de um estado inicial A a um estado final B por dois processos diferentes, indicados no diagrama P × V.

Para ocorrer, a transformação ACDEB exige uma quantidade Q1 de calor e a transformação AFB exige uma quantidade Q2 de calor.

Sendo TA e TB as temperaturas absolutas do gás nos estados A e B, respectivamente, calcule:

b) o valor da diferença Q1 – Q2, em joules.

29-(FUVEST-SP-015)

A respeito dessas transformações, afirmou-se o seguinte:

I. O trabalho total realizado no ciclo ABCA é nulo.

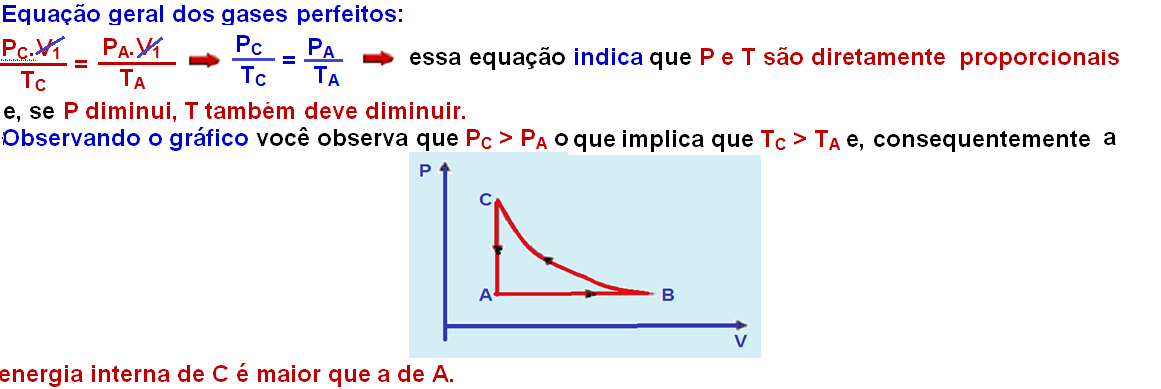
II. A energia interna do gás no estado C é maior que no estado A.

III. Durante a transformação , o gás recebe calor e realiza trabalho.

Está correto apenas o que se afirma em

Segunda lei da Termodinâmica

30-(PUC-SP-017)

Um motor de potência 2,5 c.v. absorve 925 cal/s de uma fonte térmica quente, cuja temperatura é de 927 oC.

Sendo a temperatura da fonte fria de 80,6 oF,determine a razão entre o rendimento de um motor de Carnot que operasse entre essas mesmas fontes térmicas e o rendimento do referido motor.

(A) 0,75

(B) 1,00

(C) 1,50

(D) 2,00

31-(FDSBC-SP-017)

Em uma máquina a vapor que opera segundo o ciclo de Carnot, o fluido inicia o ciclo na fonte quente a 1160,6ºF e o abandona, na fonte fria, ao sofrer uma variação de 270ºC.

Nessas condições, o rendimento máximo teórico, em porcentagem, dessa máquina é de

32-(FAMERP-SP-017)

33-(UEMG-MG-017)

Resolução Comentada – Vestibulares Recentes

Física Térmica – 2017 – 2016 – 2015

01-

R- D

03- (V) Temperatura grandeza física que representa a medida do estado de agitação médio das moléculas de um corpo.

(F) Calor energia térmica que passa, de forma espontânea, do corpo demaior temperatura para o de menor temperatura.

(F) Fusão mudança de estado físico sofrida por um sólido ao se transformar em líquido quando recebe uma certa quantidade de calor.

(V ) Evaporação passagem do estado líquido para o estado gasoso que ocorre de forma lenta.

(F) Equilíbrio térmico condição física na qual dois ou mais corpos ficam com a mesma temperatura (temperatura de equilíbrio térmico). As trocas de calor podem não cessar, e os corpos podem continuar recebendo e cedendo calor na mesma proporção.

(V ) Convecção processo de transmissão de calor que ocorre devido à movimentação de massas, em especial, nos líquidos e nos gases e essa movimentação ( massas mais quentes, menos densas sobem e as frias mais densas descem). Essa movimentação ocorre até que a massa total fique com a mesma temperatura.

(F) Caloria quantidade de calor necessária para que 1g de água tenha sua temperatura alterada em 1°C .

R- D

04- I. As prateleiras de uma geladeira doméstica são grades vazadas, para facilitar fluxo de energia térmica até o congelador por […]

Situação I Convecção

II. O único processo de troca de calor que pode ocorrer no vácuo é por […].

Situação II Radiação

III. Em uma garrafa térmica, é mantido vácuo entre as paredes duplas de vidro para evitar que o calor saia ou entre por [….].

Situação III Condução

O calor é conduzido de um ponto a outro do corpo sem que haja deslocamento das partículas.

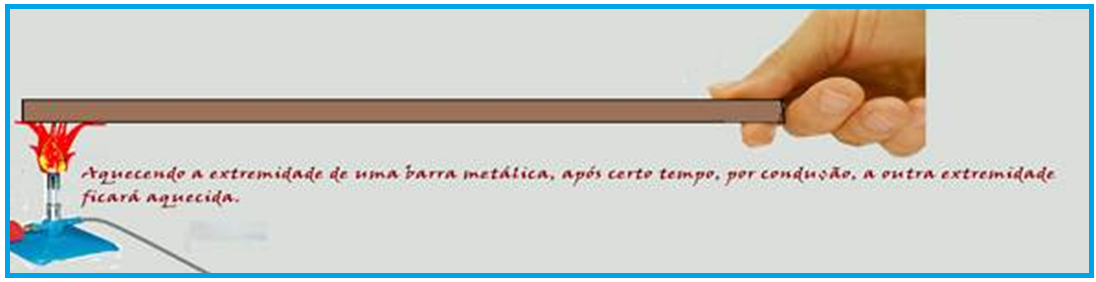
Explicando microscopicamente o fenômeno: a região próxima da chama tem o movimento vibratório de suas moléculas aumentado, adquirindo assim maior energia cinética, que é transferida através de choques às partículas vizinhas, que também aumentam seu movimento vibratório.

Através desse transporte de energia, toda a barra é aquecida.

A condução não ocorre no vácuo, pois ela precisa de um meio material para se propagar.

Na garrafa térmica, é mantido o vácuo entre as paredes de vidro para evitar trocas de calor por condução e convecção.

R- D

05-

Relação entre as escalas Celsius e Fahrenheit = = = 9C = 540 C = 60oC.

R- C

06-

07-

Como toda energia emitida pelo rádio foi absorvida pela água e empregada exclusivamente para elevar sua temperatura sempre no estado líquido indo do ponto de congelamento (0 oC) até o ponto deebulição (100 oC), a energia liberada pelo rádio foi de Q = m.c.(θ – θ_o) = 1,3.1.(100 – 0)

Q = 130 cal.

Como o experimento durou ∆t = 1 h = 3600 s, a potência média liberada pelo rádio é fornecida por

P = = = 0,14 W

R- C

08-

09-

Calor Latente

O calor recebido por um corpo pode fazer com que sua temperatura aumente ou que ele sofra uma mudança de estado. No segundo caso você tem uma quantidade de calor latente, ou seja, o calor latente se refere à quantidade de calor que um corpo recebe apenas para mudar de estado, o que ocorre à temperatura constante.

Constata-se que a quantidade de calor latente (Q) cedida ou retirada de uma substância para que ela mude de estado o que sempre ocorre à temperatura constante é diretamente proporcional à sua massa (m), e depende das características da substância (L). Matematicamente:

O calor de fusão ou de vaporização L é característica do material de que o objeto é feito independendo da massa ou do volume do objeto. Assim, se o objeto possui calor de fusão LF = 50 J/kg ele terá sempre esse valor independente de sua massa ou volume, pois o material é o mesmo.

R- C

10-

11- a) a quantidade de calor, em cal, necessária para elevar a temperatura do copo com água líquida de 20 ºC para 50 ºC.

Copo Q_c para a temperatura do copo subir de t_o = 20^o C para t = 50º C, sendo o calor específico do copo c_c = 0,2 cal/g^oC e m_c = 200 g Qc = mc.c.(t – to) =100.0,2.(50 – 20) Qc = 600 cal.

Água Q_a para a temperatura da água subir de to = 20^oC para t = 50º C, sendo o calor específico da c_a = 1 cal/g^oC e m_a = 100 g Q_a = ma.c_a.(t – t_o) = 200.1.(50 – 20) Q_c = 6000 cal.

Quantidade de calor pedida Qt = 600 + 6000 Qt = 6600 cal.

b) a massa de vapor de água, em gramas, necessária para elevar a temperatura do copo com água líquida até atingir o equilíbrio térmico a 50 ºC.

Pelo enunciado a temperatura inicial do vapor de água era t_o = 120 ^oC,que deve se transformar em água líquida a 50 ^oC. Etapas:

1^a Q₁ quantidade de calor cedida pelo vapor de água para passar de to = 120º C para t = 100º C, sem mudança de estado Q₁ = mv.cv.(t – t_o) = mv.0,5.(100 – 120) Q₁ = – 10mv.

2ª Q₂ quantidade de calor cedida pelo vapor de água para passar devapor de água a 100º C a água líquida a 100º C (condensação, liquefação) Q₂ = mv.L= mV.(-540) Q₂ = – 540mv.

3^a Q₃ quantidade de calor cedida pela água líquida para passar de t_o = 100º C para t = 50º C, sem mudança de estado Q₃ = mv.c_a.(t – to) = mv.1.(50 – 100) Q₃ = – 50mv.

Quantidade de calor cedida pelo vapor de água para se transformar em água líquida a 50oC

Q’ = Q1 + Q2 + Q3 = – 10 mv – 540mv – 50mv Q’ = – 600mv.

Essa quantidade de calor Q’ cedida pelo vapor de água para ir de 120º C a água a 50º C é a mesma recebida pelo sistema (copo + água) para ir de 20º C a 50º C (achada no item Qt = 6600 cal), ou seja, no equilíbrio térmico a soma dessas quantidades de calor trocadas entre o vapor e o copo com água deve ser nula.

- 600mv + 6600 = 0 mv = 6600/600 mv = 11 g.

12- As alternativas (A) e (E) estão erradas, pois a temperatura de fusão ou de vaporização não depende da massa do corpo, apenas do material que o constitui.

A (C) também está errada, pois a substância não é a água que sofre fusão a 0^o C.

Na fusão desse corpo de massa m = 20 g que ocorre a 50 ^oC você deve usar a expressão o calor latente fornecida por Q = m.LF (200 – 100) = 20LF LF = LF = 5 cal/g.

R- D

13- Cálculo da quantidade de calor (energia térmica) necessária para aquecer o líquido de calor específico c = 0,58 cal/g^oC com sua temperatura variando de 0o até 78^oC, sem mudança de estado Q₁ =m.c.(t – t_o) = m.0,58.(78 – 0) Q₁ = 45,24.m.

14- Para resolver esse exercício, precisamos encontrar a massa de água, então vamos utilizar as outras informações que já temos:

Analisando pela quantidade de calor:

Onde:

Q é a quantidade de calor

m é a massa

c é o calor específico

ΔT é a variação de temperatura

Isolando o m:

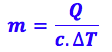Substituindo os valores:

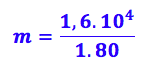Como todos os valores estão em gramas, então nosso resultado vai sair em gramas:

Agora que temos a massa, podemos usar a outra fórmula de quantidade de calor, para calcularmos a vaporização:

Onde:

Q é a quantidade de calor

m é a massa

L é o calor latente de vaporização

R – C

15-

Calculando a massa de leite densidade do leite = mL = dL.VL mL = 1 (g/mL).VL(g) mL = VL (g)

Calculando a massa de café densidade do café = mc = dc.Vc mc = 1g/mL.30 mL mc = 30 g

Após a mistura ambos terão a mesma temperatura (de equilíbrio térmico) = 40 ^oC.

R- B

16-
Princípio das trocas de calor

Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico.

Assim, como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes éigual à quantidade de calor recebida pelos mais frios.

Princípio da Conservação da energia

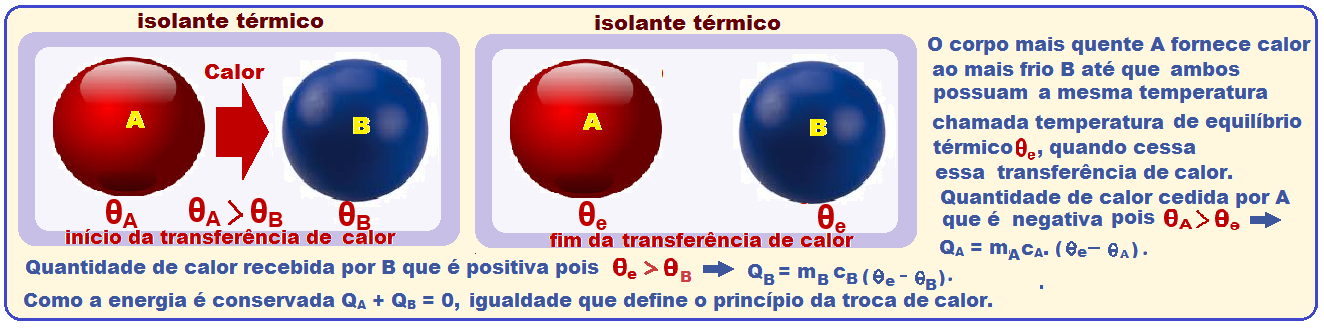
A teoria acima é válida para mais de um corpo e, como a quantidade de calor recebida é positiva e a cedida é negativa, tem-se que Q1 + Q2 + Q3 + …. + QN = 0 ou m1 .c1 .(θe – θ1 ) + m2.c2.( θe – θ2) + m3.c3.( θe –θ3) + … + mN.cN.( θe – θN) = 0.

Enunciado desse princípio das trocas de calor:

Seis horas depois, abre-se a garrafa e mede-se a temperatura da água, obtendo-se θ = 16°C.

R- D

17- Trata-se de dilatação superficial (uma das áreas) fornecida pela expressão a seguir:

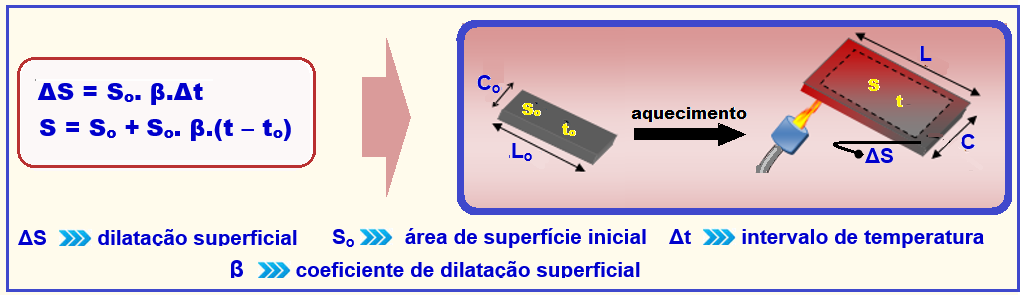
Na expressão acima, a letra grega β (beta) é uma grandeza constante, característica do material, denominada coeficiente de dilatação superficial médio.

Valor de uma das áreas S_o = L_o.L_o = 20×20 = 400 cm² β = 2. = 2.2.10-5 = 4.10^-5 ^oC^-1.

∆S = S_o.β.(t – t_o) = 400.4.10^-5.(120 – 20) = 160000.10^-5 ∆S = 16.10^-1 cm².

R- D

18- Já que o enunciado afirma que o coeficiente de dilatação do vidro utilizado é desprezível comparado ao do álcool, você deve levar em conta apenas a dilatação (∆V) do álcool de coeficiente de dilatação volumétrica = 11.10^-4 ^oC^-1, cujos volume é o do bulbo V_o = 2 cm³, pois ele é totalmente preenchido com álcool até a base do tubo. A variação de temperatura é de ∆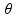 = 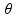- 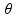_o = 80 – 30 = 50 ^oC.

Substituindo esses valores na expressão da dilatação volumétrica ∆V = Vo. = 2.11.10 ^-4.50 ∆V = 1100.10^-⁴ = 0,11 cm³.

Mas, o volume do cilindro que constitui o tubo é fornecido por ∆V = área da basexaltura = 1.10^-2.h.

O volume de líquido dilatado preenche esse cilindro até a altura h de ∆V = 1.10^-2 .h 0,11 = 0,01h h = h = 11,0 cm.

R – B

19-

20-

Capacidade térmica (C) – Calor específico (c)

Define-se capacidade térmica (C) ou capacidade calorífica de um corpo como sendo o produto da massa desse corpo pelo calor específico da substância de que ele é constituído, ou seja C = m.c como Q = m.c.Δθ Q = C.Δθ ou Q = C.(θ – θ_o).

No caso do exercício Q = C. = (I).

A dilatação térmica (variação de volume ∆V) sofrida pelo bloco é fornecida por ∆V = V_o. ., onde o coeficiente de dilatação volumétrica vale 3. sendo o coeficiente de dilatação linear do bloco ∆V = Vo. . (II).

Substituindo (I) em (II) ∆V = V_o. . .

Portanto, a variação de volume ∆V do bloco é diretamente proporcional a V_o, e inversamente proporcional a C.

R- B

21-

Dilatação linear dos sólidos

Trata-se da dilatação de uma das dimensões de um corpo, como por exemplo, seu comprimento. Considere uma haste metálica de comprimento L_o e à temperatura t_o. Quando aquecida terá comprimento L a uma temperatura t.

Características:

A dilatação linear ΔL é diretamente proporcional à variação de temperatura Δt.

A dilatação linear ΔL é diretamente proporcional ao comprimento inicial Lo.

A dilatação linear ΔL depende do material de que é constituído o corpo.

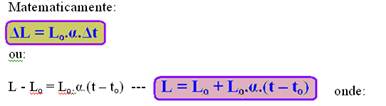
ΔL dilatação linear

α coeficiente de dilatação linear médio, característica do material que constitui a barra.

Lo comprimento inicial

L comprimento final

Δt intervalo de temperatura

Analisando as alternativas:

a) num dia de verão em que a temperatura variar 20 °C o comprimento de uma barra de ferro de 10,0 m sofrerá uma variação de 2,6 cm

a – Falsa

ΔL = Lo.α. Δt

ΔL = 10.13.10^-6.20

ΔL = 26. 10^-4 m = 0,26 cm

b) o coeficiente de dilatação superficial do ferro é 169.10^-6 ^oC^-1.

b – Falsa

 = 2.α  = 2. 13.10^-6 ºC^-1  = 26.10^-6 ºC^-1

c) para cada 1 °C de variação de temperatura, o comprimento de uma barra de 1,0 m desse material varia 13.10^-6m⋅

c – Verdadeira

ΔL = Lo.α. Δt ΔL = 1.13.10-6.1 ΔL = 13.10^-6 m

d) o coeficiente de dilatação volumétrica do ferro é 39.10^-18 ^oC^-1.

d – Falsa

 = 3.α  = 3.13.10^-6  = 39.10-6 ºC^-1

R- C

22-

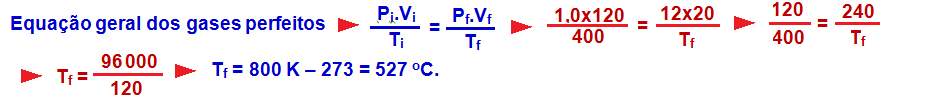
R- C

23-

Transformação adiabática

Nela, o sistema não troca calor com o meio externo (Q = 0) e isso ocorre porque o gás está termicamente isolado ou porque a transformação é muito rápida de modo que qualquer troca de calor com possa ser considerada.

Se Q = 0 ΔU = Q – W ΔU = 0 – W ΔU = – W.

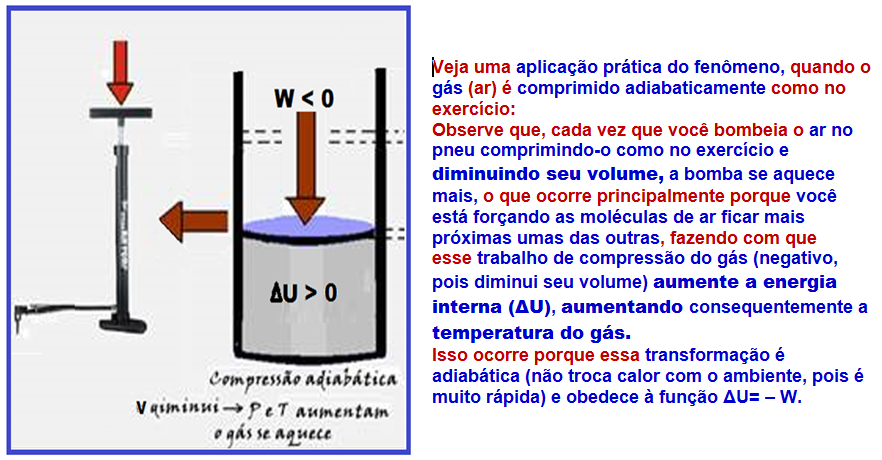
R- D

24-

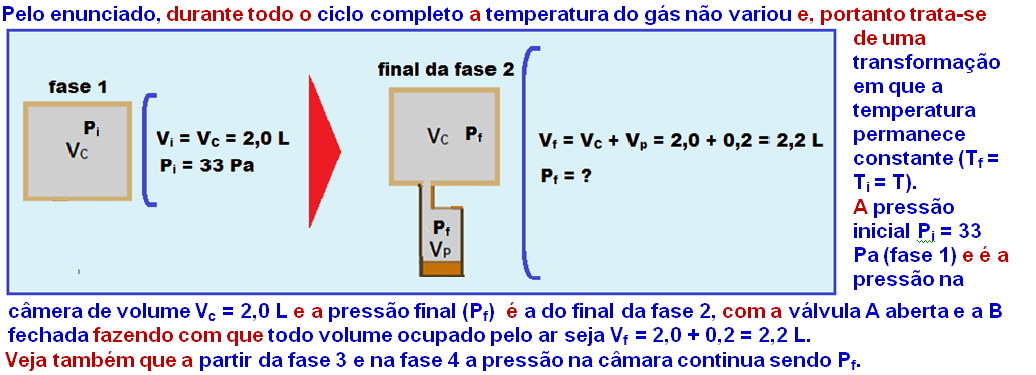
R- A

25- Para calcularmos a temperatura final precisamos primeiro do volume final. Podemos calcular visto que sabemos que o êmbolo se deslocou 10 cm:

Volume inicial = 6.10^-3 m³

Volume final = Volume inical + (volume com 10 cm de deslocamento)

Passando 10 cm para metros (dividir por 100):

10 cm = 0,1 m

Calculando :

= área interna X deslocamento

Substituindo:

= 2.10^-2.0,1

Calculando:

= 2.10^-3 m³

Agora calculando o volume final:

Volume final = 6.10^-3 + 2.10^-3

Volume final = 8.10-3 m³

Sabendo o volume final podemos utilizar a fórmula a seguir, já que se trata de um gás ideal:

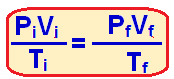
Onde:

Pi e Pf é a pressão inicial e final

Vi e Vf é o volume inicial e final

Ti e Tf é a temperatura inicial e final

Como é uma expansão isobárica (pressão constante) podemos cortar a pressão em ambos os lados, restando apenas:

Substituindo:

Isolando a temperatura final:

Tf =

Calculando:

Tf = 400 K (temperatura final)

Achamos a temperatura, agora vamos para a segunda parte do exercício. Para calcularmos a quantidade de calor vamos utilizar a primeira lei da termodinâmica. Como se trata de uma transformação isobárica:

Como a pressão é constante o nosso trabalho só depende da variação do volume:

W = P.

Substituindo. Nós calculamos a variação anteriormente (2.10^-3):

W = 2.10⁵. 2.10^-3

Calculando:

W = 4.10² J

O exercício já nos forneceu a variação de energia interna (600 J). Vamos então substituir na equação da primeira lei:

= Q – W

Isolando a quantidade de calor:

Q = + W

Substituindo:

Q = 600 + 400

Calculando:

Q = 1000 J (quantidade de calor)

26-

A) A energia interna de certa massa de um gás perfeito é função exclusiva da temperatura desse gás

Aumento de temperatura (ΔT > 0) aumento de energia interna (ΔU > 0).

Diminuição de temperatura (ΔT < 0) diminuição de energia interna (ΔU<0).

Temperatura constante (ΔT = 0) energia interna constante (ΔU = 0).

Vamos então calcular a variação da energia interna em cada transformação:

I: E = 1.105.0,6/TE = 3.105.0,2/TF 6.104 / TE = 6.104/TF TE = TF energia interna constante.

II: F 3.105.0,2/TF = 6.105.0,6/TH 6.104/TE = 6.104/TF 6.104TG = 12.104TF TF > TG TG = 2TF energia interna não constante.

III: G 6.105.0,2/TG = 4.105.0,6/TH 12.104/TG = 24.104/TH 24.104TG= 12.104TH TH = 2TH TH TG energia interna não constante.

IV: H 4.105.0,2/TH = 1.105.0,6/TE 8.104/TH = 6.104/TE 8.104TE= 6.104TH TE TH energia interna não constante.

R- A energia interna ∆U é constante apenas em I.

B) Em I não ocorre variação de energia interna.

Em II e III houve aumento de temperatura e, consequentemente aumento de energia interna.

Em IV houve diminuição de temperatura e, consequentemente diminuição de energia interna.

O aumento de enet=rgia interna ocorreu apenas em II e III e, como a energia interna é diretamente proporcional à temperatura absoluta, de A:

II. TG = 2TF = 2

III. TH = 2TG = 2

C) Veja informação abaixo:

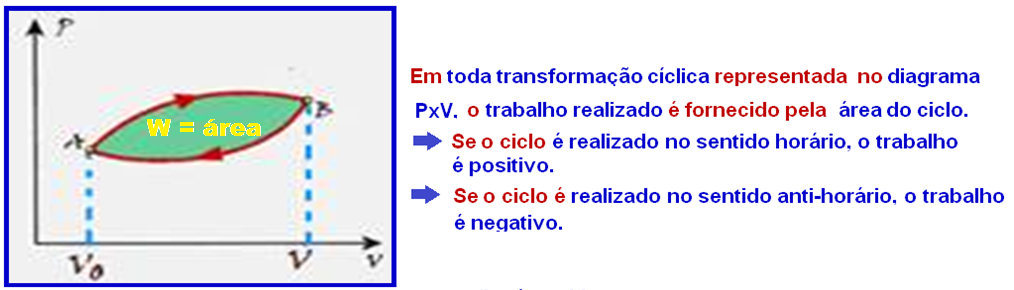
No caso doe exercício vamos calcular a área do ciclo lembrando que nos trechos FG e HE o trabalho é nulo (transformação isovlumétrica).

Cálculo do trabalho W no trecho GH onde ele fornecido pela área do trapézio e é positivo (sentido horário):

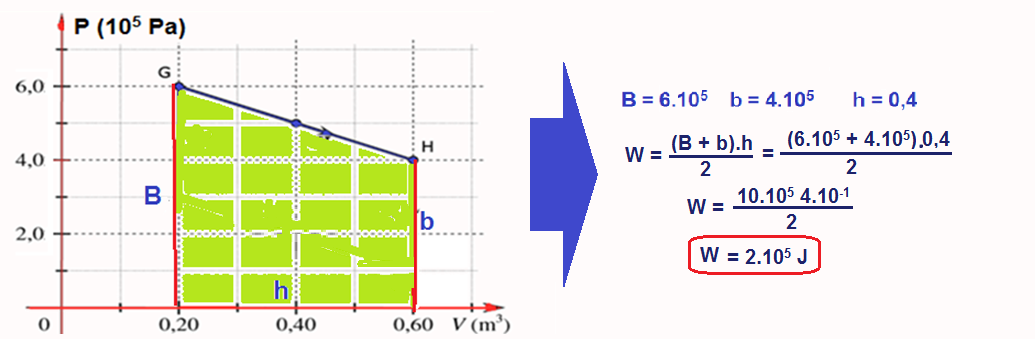
Cálculo do trabalho W no trecho EF onde ele éfornecido pela área do trapézio e é negativo (sentido anti-horário):

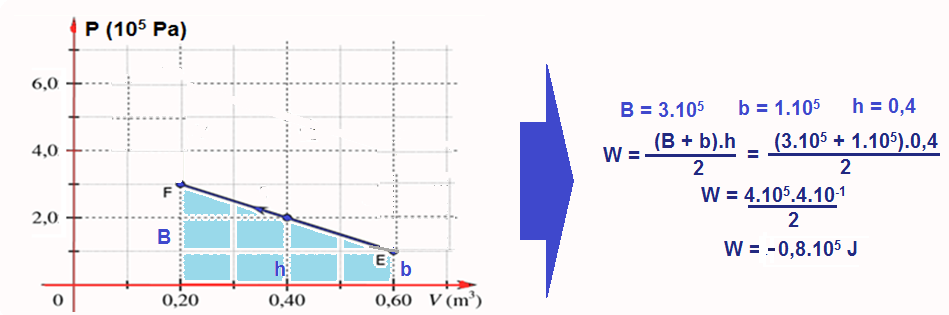
W = 2.105 – 0,8.105 = 1,2.105 J

Po = Po = = 0,02.105 Po = 2.103 W como são 50 ciclos Po = 50.2.103

Po = 100 kW.

27-

A seguir, breve resumo teórico:

Transformação isobárica

Ocorre à pressão constante. A variação de temperatura (ΔT) provoca umavariação de energia interna (ΔU) do sistema e a variação de volume (ΔV) produz trabalho.

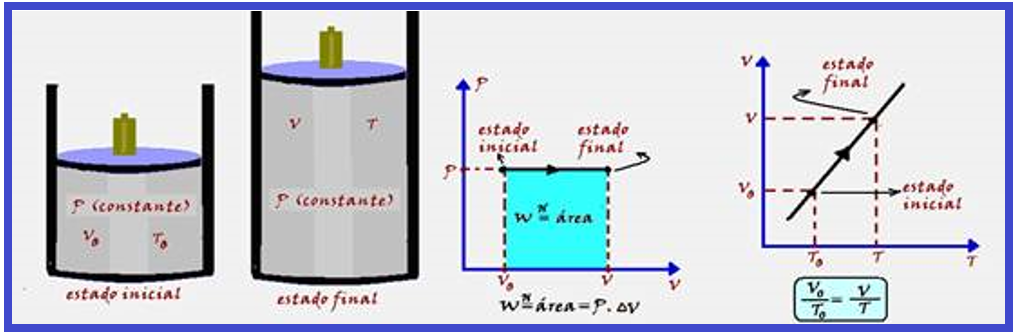
Parte do calor (Q) recebido pelo sistema é armazenada sob forma de energia interna e parte é transformada em trabalho, de modo que ΔU = Q – W.

No caso do exercício, são fornecidos:

P = constante = 1 atm = 1.10⁵ N/m² (Pa)

Volume inicial V_o = 1000 cm³ = 10³ cm³ = 10³.(10^-6 m³) Vo = 10^-3m³

Volume final que foi aumentado 300% V =( ).10^-3 V = 3.10^-3 m³

Cálculo do trabalho mecânico, em joules, realizado pelo gás durante essa transformação W = P.∆V = 10⁵.(3.10^-3 – 1.10^-3) W = 10⁵.2.10^-3 W = 2.10² J

Energia interna de um gás perfeito

A energia interna (U) de um gás perfeito monoatômico corresponde à soma das energias cinéticas médias (Ec) de todas as suas moléculas e, pela lei de Joule é fornecida por:

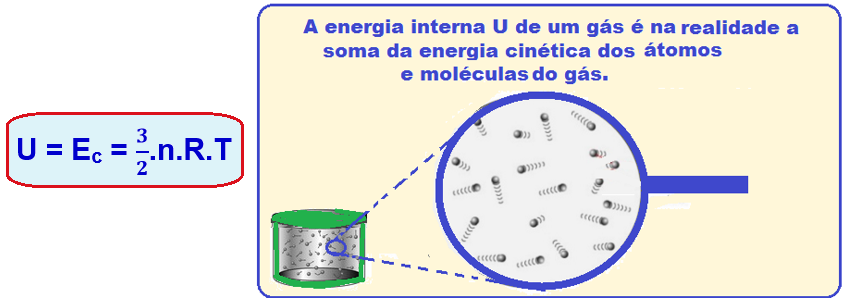
A energia interna de certa massa de um gás perfeito é função exclusiva da temperatura desse gás

Se U = (3/2).n.R.T e PV = n.R.T U = (3/2).PV ∆U = (3/2).P.∆V = ( . 10⁵.2.10^-3 ∆U = 3.10² J.

R- D

28-

Equação de Clapeyron ou Equação de um gás ideal

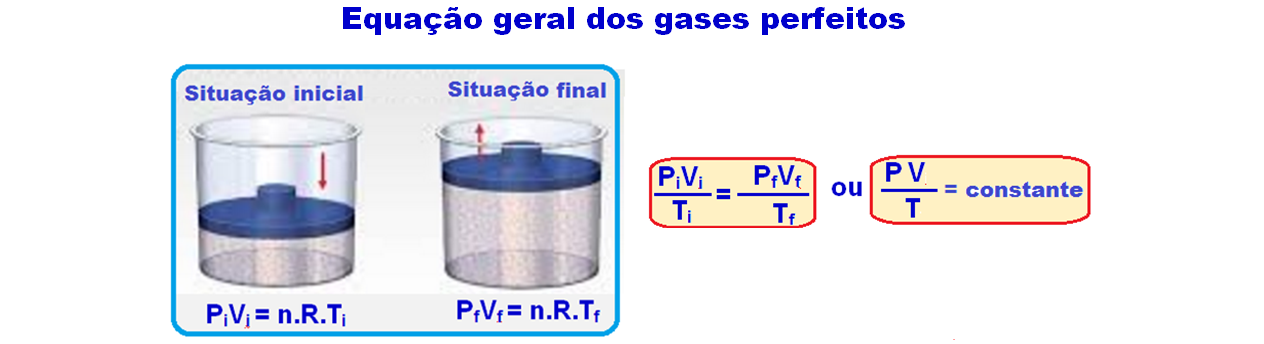
Pelo gráfico:

Ponto A PA = 2.10⁵ N/m² VA = 2.10^-3 m³ TA

Ponto B PB = 5.10⁵ N/m² VB = 6.10^-3 m³ TB

Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia

O Primeiro Princípio da Termodinâmica (Princípio da Conservação da Energia) afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”

Exemplo numérico:

Suponha que um sistema isolado receba Q = 300 J de calor. Se, por exemplo, ∆U = 50 J dessa energia forem absorvidos pelo sistema aumentando sua energia interna de 50 J, então a parte restante, W = 250 J, será fornecida ao ambiente sob forma de trabalho.

Então, Q = W + ∆U ou ∆U = Q – W.

Como nas transformações ACDEB e AFB os estados inicial (A, de temperatura TA)) e final (B, de temperatura TB) coincidem, a variação de energia interna ∆U será a mesma nas duas transformações

∆UACDEB = ∆UAFB.

∆UACDEB = Q1 – W1 e ∆UAFB = Q2 – W2 Q1 – Q2 = W1 – W2.

Mas, em toda transformação representada no diagrama PxV, o trabalho realizado é numericamente igual à área.

Cálculo do W1 no trecho ACDEB:

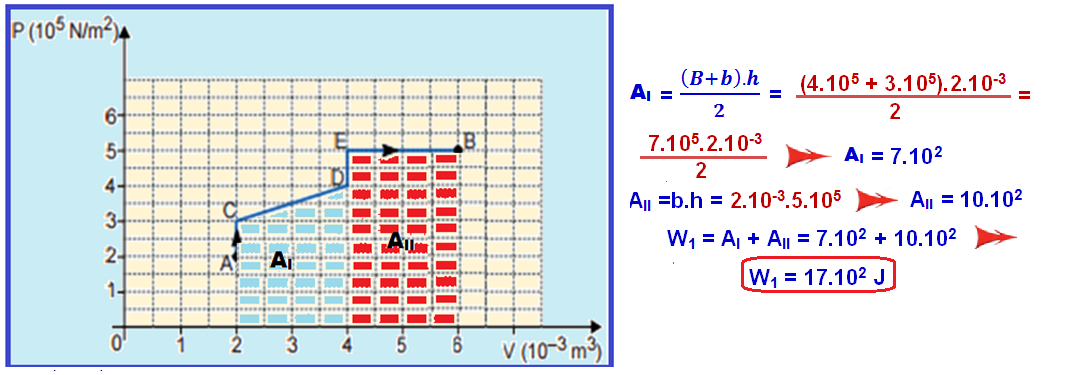
Cálculo do W2 no trecho AFB:

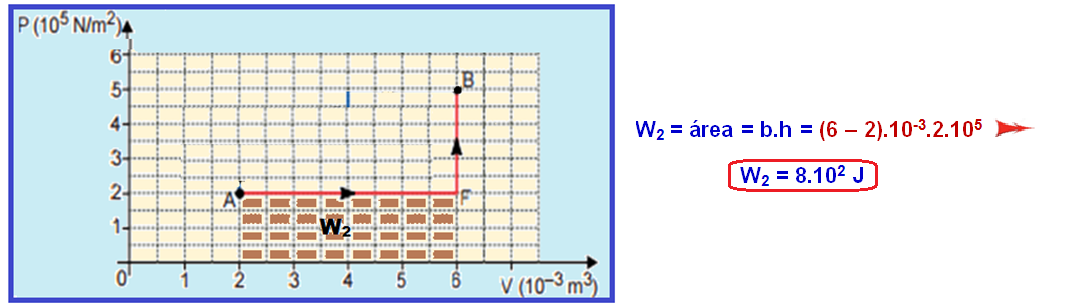
Q1 – Q2 = W1 – W2 = 17.10² – 8.10² Q1 – Q2 = 9.10² J

29-

I. O trabalho total realizado no ciclo ABCA é nulo.

I. Falsa — Em toda transformação cíclica representada no diagrama PxV, o trabalho realizado é

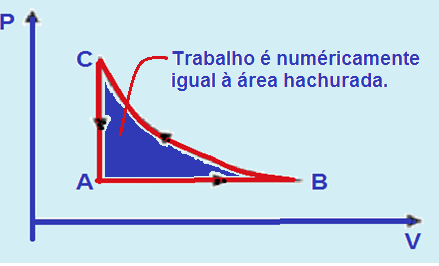
fornecido pela área do ciclo.

Se o ciclo é realizado no sentido horário, o trabalho é positivo.

Se o ciclo é realizado no sentido anti-horário, o trabalho é negativo.

II. A energia interna do gás no estado C é maior que no estado A.

II. Correto — no trecho CA a transformação é isovolumétrica onde o volume V1 é constante.

Observe nas figuras abaixo que quanto maior a temperatura maior é o movimento vibratório das

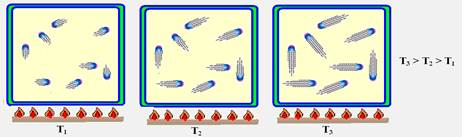
moléculas do gás e consequentemente maior a energia cinética (Ec) de suas moléculas, o que implica num aumento da energia interna (U) do gás.

III. Durante a transformação , o gás recebe calor e realiza trabalho.

Observe no gráfico que no trecho AB o volume está aumentando (VB > VA) e o trabalho realizado é positivo, pois, numa isobárica W = P.(VB – VA) e, sendo P positiva e constante e (VB – VA) > 0, o trabalho será WAB > 0.

A transformação BC é isotérmica (mesma temperatura, TB = TC) e, como vimos em I, TB=TC > TA o que implica que UB > UA fazendo com que avariação de energia interna ∆U = UB – UA seja positiva (∆UAB > 0.

Pela segunda lei da termodinâmica ∆U = Q – W QAB =∆UAB + WAB como ∆UAB e WAB são positivos, QAB > 0 e o gás recebe calor e realiza trabalho.

R- E

30-

Rendimento real η do motor

A potência total absorvida por esse motor em ∆t = 1 s vale Pt = = =

Pt = 3700 J/s Pt = 3700 W.

Potência útil do motor Pu = 2,5×740 Pu = 1850 W.

Rendimento do motor ηm =Pu/Pt = ηm = 0,5 (50%)

Rendimento de um motor de Carnot

Temperatura Tf da fonte fria Tf =927 +273 = 1200 K.

Temperatura TQ da fonte quente = = = 403 – 160 = 9C C = 27 oC TQ = 27+273 = 300 K.

O rendimento ηC de um motor de Carnot operando entre as temperaturas acima é fornecido pela expressão ηC = 1 – TQ/Tf = 1 – = 1 – 0,25 ηC = 0,75 (75%)

Razão pedida ηC/ηm = ηC/ηm = 1,5

R- C

31-

T temperatura da fonte quente T = 1 160,6 ^oF = = = 9K – 2457 = 5643 K = T = 900 K

A temperatura da fonte fria é a da fonte quente menos 270oC = 270 + 273= 543 K T1 = 900 – 543 T1 = 357 K.

Rendimento da máquina térmica = 1 – T1/T = 1 - = 1 – 0,4 = 0,6 = 60%

R – ?

32-

São dados:

Q1 quantidade de calor recebido da fonte quente num ciclo Q1 = 4,0.103 J

Q2 quantidade de calor rejeitado para a fonte fria num ciclo Q2 = 2,8.103 J

b) Cálculo do trabalho realizado em cada ciclo = Q1 – Q2 = 4,0.103 – 2,8.103 = 1,2.103 J

Como são 3000 ciclos o trabalho total será total = 1,2.103x3000 total = 3,6.106 J.

33-

η = 1 – = 1 - = 0,5 η = 50 %.

T1 = 27 + 273 = 300 K η = 1 – 0,5 = 1 – – 0,5 = – T = 600 K.

R- D

Vestibulares Recentes por assunto - 204/2013

FÍSICA TÉRMICA (TERMOLOGIA)

01-(UFPR-PR-014)

Uma pizza a 185º C foi retirada de um forno quente. Entretanto, somente quando a temperatura

atingir 65º C será possível segurar um de seus pedaços com as mãos nuas, sem se queimar. Suponha que a temperatura T da pizza, em graus Celsius, possa ser descrita em função do tempo t, em minutos, pela expressão T = 160 × 2^-0,8xt +25. Qual o tempo necessário para que se possa segurar um pedaço dessa pizza com as mãos nuas, sem se queimar?

02-(UECE-CE-014)

Considere um gás ideal que passa por dois estados, através de um processo isotérmico reversível. Sobre a pressão P e o volume V desse gás, ao longo desse processo, é correto afirmar-se que

A) PV é crescente de um estado para outro.

B) PV é constante.

C) PV é decrescente de um estado para outro.

D) PV é inversamente proporcional à temperatura do gás.

03-(UEL-PR-014)

Uma gota de álcool de 10 g, à temperatura de 70 ºC, cai em um reservatório com 1000 litros de água a

33 ºC.

Dados: Calor específico da água: 1,0 cal/g ºC

Dados: Calor específico do álcool: 0,6 cal/g ºC

Dados: Massa específica da água: 1000 kg/m3

a) Calcule a quantidade de calor transferida para a água.

b) Calcule a variação de entropia do reservatório de água. Sabendo que ΔS ≥ 0, o que se pode concluir da entropia da gota de álcool?

Apresente os cálculos.

04-(UEA-AM-014)

Um turista estrangeiro leu em um manual de turismo que a temperatura média do estado do Amazonas é de 87,8 graus, medido na escala Fahrenheit. Não tendo noção do que esse valor significa em termos climáticos, o turista consultou um livro de Física, encontrando a seguinte tabela de conversão entre escalas termométricas:

Com base nessa tabela, o turista fez a conversão da temperatura fornecida pelo manual para a escala Celsius e obteve o resultado:

(A) 25. (B) 31. (C) 21. (D) 36. (E) 16.

05-(ACAFE-SC-014)

Com 77% de seu território acima de 300m de altitude e 52% acima de 600m, Santa Catarina figura entre os estados brasileiros de mais forte relevo.

Florianópolis, a capital, encontra-se ao nível do mar.

Lages, no planalto, varia de 850 a 1200 metros acima do nível do mar.

Já o Morro da Igreja situado em Urubici é considerado o ponto habitado mais alto da Região Sul do Brasil.

A tabela abaixo nos mostra a temperatura de ebulição da água nesses locais em função da altitude.

Considere a tabela e os conhecimentos de termologia e analise as afirmações a seguir.

l Em Florianópolis os alimentos preparados dentro da água em uma panela comum são cozidos

mais depressa que em Lages, utilizando-se a mesma panela.

ll No Morro da Igreja, a camada de ar é menor, por consequência, menor a pressão atmosférica

exercida sobre a água, o que implica em um processo de ebulição a uma temperatura inferior a Florianópolis.

lll Se quisermos cozinhar em água algum alimento no Morro da Igreja, em uma panela comum, será

mais difícil que em Florianópolis, utilizando-se a mesma panela. Isso porque a água irá entrar em ebulição e secar antes mesmo que o alimento termine de cozinhar.

lV Se quisermos cozinhar no mesmo tempo em Lages e Florianópolis um mesmo alimento, devemos usar em Florianópolis uma panela de pressão.

Todas as afirmações corretas estão em:

06-(UNESP-SP-014)

Para testar os conhecimentos de termofísica de seus alunos, o professor propõe um exercício de

calorimetria no qual são misturados 100 g de água líquida a 20 ºC com 200 g de uma liga metálica a 75 ºC. O professor informa que o calor específico da água líquida é 1 cal/(g.ºC) e o da liga é 0,1 cal/

(g.ºX), onde X é uma escala arbitrária de temperatura, cuja relação com a escala Celsius está representada no gráfico.

Obtenha uma equação de conversão entre as escalas X e Celsius e, considerando que a mistura seja feita dentro de um calorímetro ideal, calcule a temperatura final da mistura, na escala Celsius, depois de atingido o equilíbrio térmico.

07-(UNESP-SP-014)

Entre 6 e 23 de fevereiro aconteceram os Jogos Olímpicos de Inverno de 2014. Dentre as diversas modalidades esportivas, o curling é um jogo disputado entre duas equipes sobre uma pista de gelo

, seu objetivo consiste em fazer com que uma pedra de granito em forma de disco fique o mais próximo de um alvo circular.

Vassouras são utilizadas pelas equipes para varrer a superfície do gelo na frente da pedra, de modo a influenciar tanto sua direção como sua velocidade.

A intensidade da fricção e a pressão aplicada pelos atletas durante o processo de varredura podem fazer com que a velocidade da pedra mude em até 20% devido à formação de uma película de água líquida entre a pedra e a pista.

O gráfico apresenta o diagrama de fases da água.

Com base nas informações constantes no texto e no gráfico, a seta que representa corretamente a transformação promovida pela varredura é a de número

08-(UNESP-SP-014)

Foram queimados 4,00 g de carvão até CO₂ em um calorímetro.

A temperatura inicial do sistema era de 20,0 ºC e a final, após a combustão, 31,3 ºC. Considere a capacidade calorífica do calorímetro = 21,4 kcal/ºC e despreze a quantidade de calor armazenada na atmosfera dentro do calorímetro. A quantidade de calor, em kcal/g, liberada na queima do carvão,

foi de

09-(UNESP-SP-014)

O gráfico representa, aproximadamente, como varia a temperatura ambiente no período de um dia, em determinada época do ano, no deserto do Saara. Nessa região a maior parte da superfície do solo é coberta por areia e a umidade relativa do ar é baixíssima.

A grande amplitude térmica diária observada no gráfico pode, dentre outros fatores, ser explicada pelo fato de que

(A) a água líquida apresenta calor específico menor do que o da areia sólida e, assim, devido a maior presença de areia do que de água na região, a retenção de calor no ambiente torna-se difícil, causando a drástica queda de temperatura na madrugada.

(B) o calor específico da areia é baixo e, por isso, ela esquenta rapidamente quando ganha calor e esfria rapidamente quando perde. A baixa umidade do ar não retém o calor perdido pela areia quando ela esfria, explicando a queda de temperatura na madrugada.

(C) a falta de água e, consequentemente, de nuvens no ambiente do Saara intensifica o efeito estufa, o que contribui para uma maior retenção de energia térmica na região.

(D) o calor se propaga facilmente na região por condução, uma vez que o ar seco é um excelente condutor de calor. Dessa forma, a energia retida pela areia durante o dia se dissipa pelo ambiente à noite, causando a queda de temperatura.

(E) da grande massa de areia existente na região do Saara apresenta grande mobilidade, causando a dissipação do calor absorvido durante o dia e a drástica queda de temperatura à noite.

10-(FUVEST-SP-014)

Uma lâmina bimetálica de bronze e ferro, na temperatura ambiente, é fixada por uma de suas extremidades, como visto na figura abaixo.

Nessa situação, a lâmina está plana e horizontal. A seguir, ela é aquecida por uma chama de gás. Após algum tempo de aquecimento, a forma assumida pela lâmina será mais adequadamente representada pela figura:

11-(AFA-014)

Um estudante, ao repetir a experiência de James P. Joule para a determinação do equivalente mecânico do calor, fez a montagem da figura abaixo.

Para conseguir o seu objetivo, ele deixou os corpos de massas M1 = 6,0 kg e M2 = 4,0 kg caírem 40 vezes com velocidade constante de uma altura de 2,0 m, girando as pás e aquecendo 1,0 kg de água contida no recipiente adiabático. Admitindo que toda a variação de energia mecânica ocorrida durante as quedas dos corpos produza aquecimento da água, que os fios e as polias sejam ideais e que o calor específico da água seja igual a 4,0 J/g°C, o aumento de temperatura dela, em °C, foi de

12-(CEDERJ-RJ-014)

Uma certa quantidade de um gás ideal ocupa a metade esquerda de um recipiente que permite troca de calor com o meio ambiente. Nestas condições, em equilíbrio térmico com o meio ambiente numa temperatura T, observa-se que a pressão do gás é P1. A válvula que mantinha o lado esquerdo (E) do recipiente com gás e o lado direito (D) vazio é aberta. O gás expande-se para todo o recipiente e termina por atingir o equilíbrio térmico com o meio ambiente, na mesma temperatura T.

Assinale a alternativa que representa as pressões finais do gás no lado esquerdo, PE, e no lado direito, PD , do recipiente.

13-(UERJ-RJ-014)

Um sistema é constituído por uma pequena esfera metálica e pela água contida em um reservatório. Na tabela, estão apresentados dados das partes do sistema, antes de a esfera ser inteiramente submersa na água.

A temperatura final da esfera, em graus Celsius, após o equilíbrio térmico com a água do

reservatório, é cerca de:

(A) 20 (B) 30 (C) 40 (D) 50

14-(UERJ-RJ-014)

Observe na tabela os valores das temperaturas dos pontos críticos de fusão e de ebulição,

respectivamente, do gelo e da água, à pressão de 1 atm, nas escalas Celsius e Kelvin.

Considere que, no intervalo de temperatura entre os pontos críticos do gelo e da água, o

mercúrio em um termômetro apresenta uma dilatação linear.

Nesse termômetro, o valor na escala Celsius correspondente à temperatura de 313 K é igual a:

15-(UFSCAR-SP-014)

Uma característica do álcool em seu estado líquido é dada pelo valor numérico 2 400 J/(kg·ºC). Essa

característica é

(A) o calor latente de vaporização, que informa a quantidade de energia térmica necessária para transformar em vapor 1 kg de álcool.

(B) o calor específico, que informa a quantidade de energia térmica necessária para que 1 kg de álcool aumente a temperatura em 1 ºC.

(C) o calor específico, que informa a quantidade de energia térmica contida em uma massa de 2 400 kg de álcool à temperatura de 1 ºC.

(D) o calor latente de condensação, que informa a quantidade de energia térmica necessária para converter em líquido1 kg de álcool.

(E) a capacidade térmica, que relaciona a quantidade de energia térmica recebida pelo álcool e a correspondente variação de temperatura provocada por ele.

16-(FGV-SP-014)

O gráfico da pressão (P), em função do volume (V) de um gás perfeito, representa um ciclo de transformações a que o gás foi submetido.

A respeito dessas transformações, é correto afirmar que a transformação

(A) AB é isobárica e que a relação TA/TB entre as temperaturas absolutas nos respectivos estados A e B vale 3.

(B) BC é isotérmica e que a relação TB/TC entre as temperaturas absolutas nos respectivos estados B e C vale 1/2.

(C) CD é isobárica e que a relação TC/TD entre as temperaturas absolutas nos respectivos estados C e D vale 2/3.

(D) AD é isotérmica e que o calor trocado com o meio ambiente nessa transformação é nulo.

(E) AD é adiabática e que o calor trocado com o meio ambiente nessa transformação é igual ao trabalho realizado pelo gás no ciclo.

17-(MACKENZIE-SP-014)

Um internauta, comunicando-se em uma rede social, tem conhecimento de que naquele instante a

temperatura em Nova Iorque é Ө_NI = 68 ºF, em Roma é Ө_RO = 291 K e em São Paulo, Ө_SP = 25 ºC. Comparando essas temperaturas, estabelece-se que

a) Ө_NI < Ө_RO < Ө_SP

b) Ө_SP < Ө_RO < Ө_NI

c) Ө_RO < Ө_NI < Ө_SP

d) Ө_RO < Ө_SP < Ө_NI

e) Ө_NI < Ө_SP < Ө_RO

18-(UDESC-SC-014)

Um sistema fechado, contendo um gás ideal, sofre um processo termodinâmico isobárico,

provocando mudança de temperatura de 200°C para 400°C. Assinale a alternativa que representa a razão aproximada entre o volume final e o inicial do gás ideal.

19-(UDESC-SC-014)

Certo metal possui um coeficiente de dilatação linear α. Uma barra fina deste metal, de comprimento Lo, sofre uma dilatação para uma dada variação de temperatura ΔT. Para uma chapa quadrada fina de lado Lo e para um cubo também de lado Lo, desse mesmo metal, se a variação de temperatura for 2ΔT, o número de vezes que aumentou a variação da área e do volume, da chapa e do cubo, respectivamente, é:

A. ( ) 4 e 6

B. ( ) 2 e 2

C. ( ) 2 e 6

D. ( ) 4 e 9

E. ( ) 2 e 8

20-(UEL-PR-014)

Em um ambiente com elevado número de indústrias e de circulação de veículos, como as regiões metropolitanas, as partículas em suspensão e os gases poluentes são levados pelas correntes de convecção para as camadas mais altas da atmosfera, onde se dissipam. O fenômeno meteorológico

da inversão térmica, que ocorre geralmente no inverno, tem como consequência o impedimento da dispersão dos poluentes, causando problemas respiratórios na população.

Assinale a alternativa que apresenta, corretamente, a causa da inversão térmica.

a) Uma massa de ar frio ascendente impede o movimento descendente de uma camada de ar quente.

b) Uma massa de ar quente descendente impede o movimento ascendente de uma camada de ar frio.

c) Uma massa de ar frio penetra entre camadas de ar quente, impedindo o movimento descendente do ar.

d) Uma massa de ar quente penetra entre camadas de ar frio, impedindo o movimento descendente do ar.

e) Uma massa de ar quente penetra entre camadas de ar frio, impedindo o movimento ascendente do ar.

Termodinâmica

Instrução: As questões 21 e 22 referem-se aos enunciados e gráfico abaixo.

O gráfico representa, em um processo isobárico, a variação em função do tempo da temperatura de uma amostra de um elemento puro cuja massa é de 1,0 kg, observada durante 9 minutos.

A amostra está no estado sólido a 0o C no instante t=0 e é aquecida por uma fonte de calor que lhe transmite energia a uma taxa de 2,0.103J/min, supondo que não haja perda de calor.

21-(UFRGS-RS-014)

A partir dos dados do gráfico, pode-se afirmar que esse elemento apresenta uma temperatura de fusão e um calor específico no estado líquido que são, respectivamente,

(A) 70º C e 180 J/(kg.K).

(B) 70º C e 200 J/(kg.K).

(C) 40º C e 150 J/(kg.K).

(D) 40º C e 180 J/(kg.K).

(E) 40º C e 200 J/(kg.K).

22-(UFRGS-RS-014)

O processo que ocorre na fase sólida envolve um trabalho total de 0,1 kJ. Nessa fase, a variação da energia interna da amostra é

23-(UNIFESP-SP-014)

Um gás ideal passa pelo processo termodinâmico representado pelo diagrama P×V. O gás, que se encontrava à temperatura de 57oC no estado inicial A, comprime-se até o estado B, pela perda de 800 J de calor nessa etapa. Em seguida, é levado ao estado final C, quando retorna à temperatura inicial. A linha tracejada representa uma isoterma.

Considerando os valores indicados no gráfico e que a massa do gás tenha permanecido constante durante todo o processo, calcule:

a) a temperatura do gás, em graus Celsius, no estado B.

b) o calor, em joules, recebido pelo gás de uma fonte externa, quando foi levado do estado B para o estado final C.

24-(UNESP-SP-014)

A figura representa um cilindro contendo um gás ideal em três estados, 1, 2 e 3, respectivamente.

No estado 1, o gás está submetido à pressão P₁ = 1,2.10⁵ Pa e ocupa um volume V₁ = 0,008 m³ à temperatura T₁.

Acende-se uma chama de potência constante sob o cilindro, de maneira que ao receber 500 J de calor o gás sofre uma expansão lenta e isobárica até o estado 2, quando o êmbolo atinge o topo do cilindro e é impedido de continuar a se mover. Nesse estado, o gás passa a ocupar um volume V₂ = 0,012 m³ à temperatura T₂.

Nesse momento, o êmbolo é travado de maneira que não possa mais descer e a chama é apagada.

O gás é, então, resfriado até o estado 3, quando a temperatura volta ao valor inicial T₁ e o gás fica submetido a uma nova pressão P₃.

Considerando que o cilindro tenha capacidade térmica desprezível, calcule a variação de energia interna sofrida pelo gás quando ele é levado do estado 1 ao estado 2 e o valor da pressão final P₃.

25-(AFA-014)

Dispõe-se de duas máquinas térmicas de Carnot. A máquina 1 trabalha entre as temperaturas de 227

°C e 527 °C, enquanto a máquina 2 opera entre 227 K e 527 K.

Analise as afirmativas a seguir e responda ao que se pede.

I. A máquina 2 tem maior rendimento que a máquina 1.

II. Se a máquina 1 realizar um trabalho de 2000 J terá retirado 6000 J de calor da fonte quente.

III. Se a máquina 2 retirar 4000 J de calor da fonte quente irá liberar aproximadamente 1720 J de calor para a fonte fria.

IV. Para uma mesma quantidade de calor retirada da fonte quente pelas duas máquinas, a máquina 2 rejeita mais calor para a fonte fria.

São corretas apenas

26-(UDESC-SC-014)

Analise as duas situações:

I. Um processo termodinâmico adiabático em que a energia interna do sistema cai pela metade.

II. Um processo termodinâmico isovolumétrico em que a energia interna do sistema dobra.

Assinale a alternativa incorreta em relação aos processos termodinâmicos I e II.

A. ( ) Para a situação I o fluxo de calor é nulo, e para a situação II o trabalho termodinâmico é nulo.

B. ( ) Para a situação I o fluxo de calor é nulo, e para a situação II o fluxo de calor é igual à energia interna inicial do sistema.

C. ( ) Para a situação I o trabalho termodinâmico é igual à energia interna inicial do sistema, e para a situação II o fluxo de calor é igual à energia interna final do sistema.

D. ( ) Para a situação I o trabalho termodinâmico é a metade da energia interna inicial do sistema, e para a situação II o trabalho termodinâmico é nulo.

E. ( ) Para ambas situações, a variação da energia interna do sistema é igual ao fluxo de calor menos o trabalho termodinâmico.

27-(UEL-PR-014)

A Revolução Industrial foi acompanhada por profundas transformações na Europa. Os novos meios

de transporte, que utilizavam as máquinas térmicas recém-criadas, foram essenciais aos avanços relacionados à industrialização por todo o continente.

Naquele período, foi demonstrado teoricamente que uma máquina térmica ideal é aquela que descreve um ciclo especial, denominado ciclo de Carnot.

Sobre os princípios físicos da termodinâmica e do ciclo de Carnot, assinale a alternativa correta.

a) As máquinas térmicas, que operam em ciclos, são incapazes de retirar o calor de uma fonte e o transformar integralmente em trabalho.

b) Em uma máquina térmica que opera em ciclos de Carnot, ocorrem duas transformações isobáricas e duas isovolumétricas.

c) No ciclo de Carnot, ocorre uma transformação reversível, enquanto as demais são irreversíveis.

d) O rendimento de uma máquina térmica é nulo quando as etapas do ciclo de Carnot forem transformações reversíveis.

e) Uma máquina térmica é capaz de transferir calor de um ambiente frio para um quente sem a necessidade de consumir energia externa.

Termometria – medida de temperatura

36-(AFA-013)

Dois termômetros idênticos, cuja substância termométrica é o álcool etílico, um deles graduado na

escala Celsius e o outro graduado na escala Fahrenheit, estão sendo usados simultaneamente por um aluno para medir a temperatura de um mesmo sistema físico no laboratório de sua escola. Nessas condições, pode-se afirmar corretamente que

a) os dois termômetros nunca registrarão valores numéricos iguais.

b) a altura da coluna líquida será igual nos dois termômetros, porém com valores numéricos sempre diferentes.

c) a unidade de medida do termômetro graduado na escala Celsius é 1,8 vezes maior que a da escala Fahrenheit.

d) a altura da coluna líquida será diferente nos dois termômetros

37-(ESPEX-013)

Um termômetro digital, localizado em uma praça da Inglaterra, marca a temperatura de 10,4 °F. Essa

temperatura, na escala Celsius, corresponde a

Propagação do calor

69-(UEL-PR-013)

O cooler, encontrado em computadores e em aparelhos eletroeletrônicos, é responsável pelo resfriamento do microprocessador e de outros componentes. Ele contém um ventilador que faz circular ar entre placas difusoras de calor. No caso de computadores, as placas difusoras ﬁcam em contato direto com o processador, conforme a ﬁgura a seguir.

Sobre o processo de resfriamento desse processador, assinale a alternativa correta.

a) O calor é transmitido das placas difusoras para o processador e para o ar através do fenômeno de radiação.

b) O calor é transmitido do ar para as placas difusoras e das placas para o processador através do fenômeno de convecção.

c) O calor é transmitido do processador para as placas difusoras através do fenômeno de condução.

d) O frio é transmitido do processador para as placas difusoras e das placas para o ar através do fenômeno de radiação.

e) O frio é transmitido das placas difusoras para o ar através do fenômeno de radiação.

70-(PUC-GO-013)

A Groenlândia nunca Derreteu Tanto

Texto: No verão da Groenlândia, é normal que suas camadas de gelo se derretam. Em julho de 2012,

no entanto, em apenas quatro dias (de 9 a 12) a superfície gelada sofreu um derretimento nunca observado: a área descongelada passou de 40% para 97%. Apesar de os cientistas definirem o fenômeno como “extremo”, eles explicam que não há motivos para alarde: experimentos apontaram que, nos últimos dez milênios, houve um vasto derretimento a cada 150 anos.

As informações são da Nasa.

(PRADO, Antônio Carlos; DAUDÉN, Laura. A Groenlândia nunca derreteu tanto. Istoé, São paulo, n. 2.229,

p. 28, 27 jul. 2012.)

Sobre esse tema, analise os itens abaixo:

I - Gases de “efeito estufa” contribuem para o aquecimento global por absorver radiação mais infravermelha que visível.

II - A principal fonte de energia da Terra é a radiação.

III - A Superfície do Planeta Terra perde energia para o espaço exterior devido, principalmente, à convecção.

De acordo com os itens analisados, marque a alternativa correta:

A ( ) Apenas I e II são verdadeiros. B ( ) Apenas I e III são verdadeiros.

C ( ) Apenas II e III são verdadeiros. D ( ) I, II e III são verdadeiros.

71-(UNESP-SP-013)

Por que o deserto do Atacama é tão seco?

A região situada no norte do Chile, onde se localiza o deserto do Atacama, é seca por natureza. Ela

sofre a influência do Anticiclone Subtropical do Pacífico Sul (ASPS) e da cordilheira dos Andes.

O ASPS, região de alta pressão na atmosfera, atua como uma “tampa”, que inibe os mecanismos de levantamento do ar necessários para a formação de nuvens e/ou chuva.

Nessa área, há umidade perto da costa, mas não há mecanismo de levantamento. Por isso não chove. A falta de nuvens na região torna mais intensa a incidência de ondas eletromagnéticas vindas do Sol, aquecendo a superfície e elevando a temperatura máxima. De noite, a Terra perde calor mais rapidamente, devido à falta de nuvens e à pouca umidade da atmosfera, o que torna mais baixas as temperaturas mínimas. Essa grande amplitude térmica é uma característica dos desertos.

(Ciência Hoje, novembro de 2012. Adaptado.)

Baseando-se na leitura do texto e dos seus conhecimentos de processos de condução de calor, é correto afirmar que o

ASPS e a escassez de nuvens na região do Atacama .

As lacunas são, correta e respectivamente, preenchidas por

(A) favorece a convecção – favorece a irradiação de calor

(B) favorece a convecção – dificulta a irradiação de calor

(C) dificulta a convecção – favorece a irradiação de calor

(D) permite a propagação de calor por condução – intensifica o efeito estufa

(E) dificulta a convecção – dificulta a irradiação de calor

72-(UNICAMP-SP-013)

A boa ventilação em ambientes fechados é um fator importante para o conforto térmico em regiões de clima quente. Uma chaminé solar pode ser usada para aumentar a ventilação de um edifício. Ela

faz uso da energia solar para aquecer o ar de sua parte superior, tornando-o menos denso e fazendo com que ele suba, aspirando assim o ar dos ambientes e substituindo-o por ar vindo do exterior.

a) A intensidade da radiação solar absorvida por uma placa usada para aquecer o ar é igual a 400 W/m². A energia absorvida durante 1,0 min por uma placa de 2 m² é usada para aquecer 6,0 kg de ar. O calor específico do ar é c=1000 J/kg.^oC.

Qual é a variação de temperatura do ar nesse período?

b) A densidade do ar a 290 K é ρ=1,2 kg/m³ . Adotando-se um número fixo de moles de ar mantido a pressão constante, calcule a sua densidade para a temperatura de 300 K. Considere o ar como um gás ideal.

Termologia

Conceitos iniciais

22-(PUC-MG-013)

O gás de cozinha é constituído principalmente de butano e é comercializado basicamente nos botijões de 13 Kg.

Se se agitar um desses botijões, nota-se que em seu interior existe uma grande quantidade de líquido. Por outro lado, quando os queimadores estão abertos, o que chega aos bicos é material em estado gasoso. Sobre essa situação, é CORRETO afirmar:

a) Quando o butano vai do botijão até os queimadores, ele se aquece e passa do estado líquido para o estado gasoso.

b) Quando o butano está no interior, a pressão sobre ele é suficiente para que a maioria do material se apresente na forma líquida.

c) Na realidade o butano chega aos queimadores no estado líquido e só toma a forma gasosa devido ao calor vindo da queima.

d) O butano só se torna gasoso ao chegar aos queimadores, porque ele é um produto inflamável.

Calorimetria

Calor sensível (específico) e trocas de calor sem mudança de estado

73-(UNIMONTES-MG-013)

Em uma banheira, a temperatura ideal da água para o banho é de 30°C. A banheira está inicialmente

com 25 litros de água a 45°C.

Uma torneira que abastece a banheira tem vazão de 10 litros por minuto. A água da torneira está a 18°C.

As trocas de calor acontecem apenas entre a água da torneira e a água da banheira. O tempo mínimo para que a água da banheira esteja boa para o banho, em segundos, e o volume de água na banheira, em litros, decorrido esse tempo, são, respectivamente:

A) 178,5 e 56,25.

B) 187,5 e 56,52.

C) 187,5 e 56,25.

D) 187,52 e 56,25.

74-(UNIOESTE-PR-013)

Em um recipiente de capacidade térmica desprezível são colocados dois líquidos de calores

específicos c₁ e c₂ a temperaturas iniciais t₁ e t₂, respectivamente. Após algum tempo os líquidos, que possuem massas iguais, atingem o equilíbrio térmico.

Considerando a situação descrita, pode-se expressar a temperatura final, t_f, da mistura por meio

da equação

75-(MACKENZIE-SP-013)

Um estudante no laboratório de física, por descuido, colocou 200 g de água liquida (calor específico

1 cal/(g.ºC)) a 100ºC no interior de um calorímetro de capacidade térmica 5 cal/ºC, que contém 100 g de água a 20 ºC.

A massa de água líquida a 0 ºC, que esse aluno deverá adicionar no calorímetro, para que a temperatura de equilíbrio térmico volte a ser 20 ºC, é

a) 900 g b) 800 g c) 700 g d) 600 g e) 500 g

76-(UNICAMP-SP013)

Uma barra cilíndrica é aquecida a uma temperatura de 740°C. Em seguida, é exposta a uma corrente de ar a 40°C.

Sabe-se que a temperatura no centro do cilindro varia de acordo com a função T(t) = (T_o – T_ar).10 – t/12 + T_ar, sendo t o tempo em minutos, T_o a temperatura inicial e T_ar a temperatura do ar.

Com essa função, concluímos que o tempo requerido para que a temperatura no centro atinja 140°C é dado pela seguinte expressão, com o log na base 10:

a) 12[log(7) – 1] minutos.

b) 12[1 – log(7)] minutos.

c) 12log(7) minutos.

d) [(1 – log(7)/12 minutos

77- UNICAMP-SP-013)

faz uso da energia solar para aquecer o ar de sua parte superior, tornando-o menos denso e fazendo com que ele suba, aspirando assim o ar dos ambientes e substituindo-o por ar vindo do exterior.

Calor Latente – trocas de calor com mudança de estado

57-(UDESC-SC-013)

Assinale a alternativa que corresponde à temperatura final de equilíbrio quando 10,0g de gelo à

temperatura de -10,0^oC são adicionados a 90,0g de água à temperatura de 50,0^oC.

Dados: calor específico do gelo --- c_gelo=0,5cal/g^oC, calor específico da água --- cágua=1 cal/g^oC, calor latente de fusão do gelo --- L=80cal/g

A. ( ) 34,2^oC B. ( ) 40,3^oC C. ( ) 36,5^oC D. ( ) 42,0^oC E. ( ) 35,1^oC

58-(PUCCAMP-SP-013)

A radiação solar incidente na superfície da Terra provoca a evaporação da água, formando as nuvens.

Esse processo ocorre rapidamente com a água contida em uma panela, aberta à pressão atmosférica normal, ao receber o calor produzido pela combustão do gás de cozinha.

Considere uma porção de 0,50 kg de água, inicialmente a 20 °C, sendo totalmente vaporizada a 100 °C. Seja: c_água=4,2.103J/kg^oC e L_{vaporização}=2,26.10⁶J/kg.

A energia recebida por essa porção de água até a sua vaporização total é, em joules, de

(A) 1,68.10³ (B) 2,81.10³ (C) 1,13.10⁶ (D) 1,30.10⁶ (E) 2,60.10⁴

59-(PUC-RJ-013)

Três cubos de gelo de 10,0 g, todos eles a 0,0^oC, são colocados dentro de um copo vazio e expostos

ao sol até derreterem completamente, ainda a 0,0^oC.

Calcule a quantidade total de calor requerida para isto ocorrer, em calorias.

Considere o calor latente de fusão do gelo L_F= 80 cal/g

(A) 3,7.10¹ (B) 2,7.10¹ (C) 1,1.10² (D) 8,0.10² (E) 2,4.10³

60-(MACKENZIR-SP-013)

Uma das características meteorológicas da cidade de São Paulo é a grande diferença de temperatura registrada em um mesmo instante entre diversos pontos do município. Segundo dados do Instituto Nacional de Meteorologia, a menor temperatura registrada nessa cidade foi – 2 ºC, no dia 2 de agosto de 1955, embora haja algumas indicações, não oficiais, de que, no dia 24 de agosto de 1898, registrou-se a temperatura de – 4 ºC.

Em contrapartida, a maior temperatura teria sido 37 ºC, medida em 20 de janeiro de 1999. Considerando-se 100 g de água, sob pressão atmosférica normal, incialmente a – 4 ºC, para chegar a 37 ºC, a quantidade de Energia Térmica que esta massa deverá receber é

a) 11,3 kcal b) 11,5 kcal c) 11,7 kcal d) 11,9 kcal e) 12,1 kcal

61-(UNIFESP-SP-013)

O gráfico representa o processo de aquecimento e mudança de fase de um corpo inicialmente na

fase sólida, de massa igual a 100 g. Sendo Q a quantidade de calor absorvida pelo corpo, em calorias, e T a temperatura do corpo, em graus Celsius, determine:

a) o calor específico do corpo, em cal/(g ºC), na fase sólida e na fase líquida.

b) a temperatura de fusão, em ºC, e o calor latente de fusão, em cal/g, do corpo.

Dilatometria

Dilatação linear, superficial e volumétrica

78-(UEM-SC-013)

Uma barra homogênea de 50 cm de comprimento e 1 kg de massa, a 20ºC, é constituída por uma

substância de coeficiente de dilatação linear de 2.10^-6 ºC^-1 e calor específico de 0,5 cal/(gºC).

Uma certa quantidade de calor é fornecida à barra, e sua temperatura é elevada a 50 ºC.

Desprezando as perdas de calor para o meio, analise as alternativas abaixo e assinale o que for correto.

01) A quantidade de calor fornecida à barra é de aproximadamente 1,5.10⁴ cal.

02) A variação do comprimento da barra é de aproximadamente 3.10^-3 cm.

04) A capacidade térmica da barra é de aproximadamente 500 cal/ºC.

08) Se o coeficiente de dilatação linear da barra fosse o dobro, a quantidade de calor necessário para variar a

temperatura da barra de 20ºC até 50ºC seria de aproximadamente 3,0.10⁴ cal.

16) A densidade linear de massa da barra permanece perfeitamente inalterada quando a barra é aquecida de 20ºC até 50ºC.

79-(AFA-013)

No gráfico a seguir, está representado o comprimento L de duas barras A e B em função da temperatura θ.

Sabendo-se que as retas que representam os comprimentos da barra A e da barra B são paralelas, pode-se afirmar que a razão entre o coeficiente de dilatação linear da barra A e o da barra B é

a) 2,00. b) 0,50 c) 1,00. d) 0,25.

Termodinâmica

Mudanças de estado físico

52-(UNESP-SP-013)

A liofilização é um processo de desidratação de alimentos que, além de evitar que seus nutrientes saiam junto com a água, diminui bastante sua massa e seu volume, facilitando o armazenamento e o transporte. Alimentos liofilizados também têm seus prazos de validade aumentados, sem perder características como aroma e sabor.

O processo de liofilização segue as seguintes etapas:

I. O alimento é resfriado até temperaturas abaixo de 0 ºC, para que a água contida nele seja solidificada.

II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada.

Dessa forma, a água sai do alimento sem romper suas estruturas moleculares, evitando perdas de proteínas e vitaminas.

O gráfico mostra parte do diagrama de fases da água e cinco processos de mudança de fase, representados pelas setas numeradas de 1 a 5.

A alternativa que melhor representa as etapas do processo de liofilização, na ordem descrita, é

(A) 4 e 1. (B) 2 e 1. (C) 2 e 3. (D) 1 e 3. (E) 5 e 3.

Transformações gasosas

52-(PUC-RJ-013)

Um sistema termodinâmico recebe certa quantidade de calor de uma fonte quente e sofre uma expansão isotérmica indo do estado 1 ao estado 2, indicados na figura.

Imediatamente após a expansão inicial, o sistema sofre uma segunda expansão térmica, adiabática, indo de um estado 2 para o estado 3 com coeficiente de Poisson λ=1,5.

a) Determine o volume ocupado pelo gás após a primeira expansão, indo do estado 1 ao estado 2.

b) Determine a pressão no gás quando o estado 3 é atingido.

53-(PUC-RS-013)

Pode-se escrever a equação geral dos gases na forma P₁/T₁μ₁= P₂/T₂μ₂ , onde P, T e μ são respectivamente a pressão, a temperatura e a massa específica do gás. A 10km de altitude acima do nível do mar, encontram-se importantes rotas

nível do mar, encontram-se importantes rotas aéreas.

Nessa altitude, a pressão é p₂=0,26 atm e a temperatura é T₂= -50ºC (223K). Tomando como referência o nível do mar, onde a pressão é p₁=1,00 atm e a temperatura é T₁=15ºC (288K), e o nível a 10 km de altitude, verifica-se que P₂/P₁=0,26 e T₁/T₂≈1,3.

Assim sendo, a razão entre as massas específicas do ar μ₂/μ₁ nas respectivas altitudes é, aproximadamente,

A) 2,94 B) 2,20 C) 1,00 D) 0,52 E) 0,34

54-(UNESP-SP-013)

O processo de liofilização segue as seguintes etapas:

I. O alimento é resfriado até temperaturas abaixo de 0 ºC, para que a água contida nele seja solidificada.

II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada. Dessa forma, a água sai do alimento sem romper suas estruturas moleculares, evitando perdas de proteínas e vitaminas.

O gráfico mostra parte do diagrama de fases da água e cinco processos de mudança de fase, representados pelas setas numeradas de 1 a 5.

A alternativa que melhor representa as etapas do processo de liofilização, na ordem descrita, é

(A) 4 e 1. (B) 2 e 1. (C) 2 e 3. (D) 1 e 3. (E) 5 e 3.

Trabalho de um gás – transformação cíclica

27-(UFV-MG-013)

O gráfico abaixo representa uma transformação cíclica de um gás ideal. É CORRETO afirmar que a

quantidade de calor trocado entre o gás e a sua vizinhança nesse ciclo é:

a) 64 J b) 16 J c) 32 J d) 48 J

28-(UNESP-SP-013)

Determinada massa de gás ideal sofre a transformação cíclica ABCDA mostrada no gráfico. As transformações AB e CD são isobáricas, BC é isotérmica e DA é adiabática.

Considere que, na transformação AB, 400 kJ de calor tenham sidos fornecidos ao gás e que, na transformação CD, ele tenha perdido 440 kJ de calor para o meio externo.

Calcule o trabalho realizado pelas forças de pressão do gás na expansão AB e a variação de energia interna sofrida pelo gás na transformação adiabática DA.

29-(UFV-MG-013)

O gráfico abaixo representa uma transformação cíclica de um gás ideal. É CORRETO afirmar que a

quantidade de calor trocado entre o gás e a sua vizinhança nesse ciclo é:

a) 64 J b) 16 J c) 32 J d) 48 J

Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia

58-(UFRN-RN-013)

A biomassa é uma das principais fontes de energia renovável e, portanto, máquinas que a utilizam como combustível para geração de energia são importantes do ponto de vista ambiental. Um exemplo bastante comum é o uso da biomassa com o objetivo de acionar uma turbina a vapor para gerar trabalho. A figura ao lado mostra, esquematicamente, uma usina termoelétrica simplificada.

Nessa termoelétrica, a queima da biomassa na fornalha produz calor, que aquece a água da caldeira e gera vapor a alta pressão.

O vapor, por sua vez, é conduzido por tubulações até a turbina que, sob a ação deste, passa a girar suas pás.

Considere desprezíveis as perdas de calor devido às diferenças de temperatura entre as partes dessa máquina térmica e o ambiente. Nesse contexto, a variação da energia interna da água da caldeira

A) é maior que a soma do calor a ela fornecido pela queima da biomassa com o trabalho realizado sobre a turbina.

B) é igual à soma do calor a ela fornecido pela queima da biomassa com o trabalho realizado sobre a turbina.

C) é igual à diferença entre o calor a ela fornecido pela queima da biomassa e o trabalho realizado sobre a turbina.

D) é maior que a diferença entre calor a ela fornecido pela queima da biomassa e o trabalho realizado sobre a turbina.

59-(UNESP-SP-013)

Determinada massa de gás ideal sofre a transformação cíclica ABCDA mostrada no gráfico. As transformações AB e CD são isobáricas, BC é isotérmica e DA é adiabática. Considere que, na transformação AB, 400 kJ de calor tenham sidos fornecidos ao gás e que, na transformação CD, ele tenha perdido 440 kJ de calor para o meio externo.

Calcule o trabalho realizado pelas forças de pressão do gás na expansão AB e a variação de energia interna sofrida pelo gás na transformação adiabática DA.

Segunda lei da Termodinâmica

49-(ENEM-MEC-012)

Aumentar a eficiência na queima de combustível dos motores a combustão e reduzir suas emissões

de poluentes é a meta de qualquer fabricante de motores. É também o foco de uma pesquisa brasileira que envolve experimentos com plasma, o quarto estado da matéria e que está presente no processo de ignição.

A interação da faísca emitida pela vela de ignição com as moléculas de combustível gera o plasma que provoca a explosão liberadora de energia que, por sua vez, faz o motor funcionar. Disponível em: www.inovacaotecnologica.com.br. Acesso em: 22 jul. 2010 (adaptado).

No entanto, a busca da eficiência referenciada no texto apresenta como fator limitante

a) o tipo de combustível, fóssil, que utilizam. Sendo um insumo não renovável, em algum momento estará esgotado.

b) um dos princípios da termodinâmica, segundo o qual o rendimento de uma máquina térmica nunca atinge o ideal.

c) o funcionamento cíclico de todos os motores. A repetição contínua dos movimentos exige que parte da energia seja transferida ao próximo ciclo.

d) as forças de atrito inevitável entre as peças. Tais forças provocam desgastes contínuos que com o tempo levam qualquer material à fadiga e ruptura.

e) a temperatura em que eles trabalham. Para atingir o plasma, é necessária uma temperatura maior que a de fusão do aço com que se fazem os motores.

50-(UFV-MG-013)

As afirmativas abaixo comparam o rendimento de duas máquinas térmicas. Analise cada uma das,

afirmativas, atribuindo V para as verdadeiras e F para as falsas:

( ) A máquina que tem o maior rendimento é a que produz a maior quantidade de trabalho.

( ) Se as duas máquinas produzem a mesma quantidade de trabalho, a que tem o maior rendimento é a que gastou o menor tempo para produzir tal trabalho.

( ) A máquina que tem o maior rendimento é a que retira a menor quantidade de calor do reservatório quente.

Assinale a sequência CORRETA:

a) F, V, F. b) V, F, V. c) F, F, F. d) V, V, V.

51-(FMABC-SP-013)

Determinada máquina térmica foi projetada para operar realizando o ciclo de Carnot. Quando em operação, o trabalho útil fornecido pela máquina, a cada ciclo, é de 3200J. As temperaturas das fontes térmicas são 427°C e 77°C, respectivamente.

Nestas condições, a quantidade de calor retirada da fonte quente, a quantidade de calor rejeitada para a fonte fria e o rendimento da máquina térmica são, respectivamente, iguais a:

Adote 4J = 1cal

(A) 3900J, 700J, 82%

(B) 6400J, 3200J, 50%

(C) 3200J, 6400J, 50%

(D) 700J, 3900J, 82%

(E) 1600J, 3200J, 50%

Vestibulares Recentes – Resolução Comentada

FÍSICA TÉRMICA – 2014/2013

01- Quando a temperatura for de T=185^oC --- 185=160.2^-0,8t + 25 --- 160=160.2^-0,8t --- 160/160=2^-0,8t --- 1=2^-0,8t --- 2⁰=2^-0,8t --- 0,8t=0 --- t=0 (quando T=185^oC, começou a contagem do tempo) --- quando a temperatura for de T=65^oC --- 65=160.2^-0,8t + 25 --- 40=160.2^-0,8t --- 40/160=2^-0,8t --- 1/4=2^-0,8t --- 2^-2=2^-0,8t --- 0,6t=2 --- t=20/8=2,5min --- R- C

02-

Transformação isotérmica

Nela, durante todo o processo, a temperatura permanece constante (isso=igual; termos= temperatura). O cientista Robert Boyle comprovou que, quando a temperatura é constante, a pressão (P) exercida por certa massa gasosa é inversamente proporcional ao volume (V) por ela ocupado --- ou --- P.V=constante --- ou ainda --- P_o.V_o=P.V --- P_o e V_o representam a pressão e o volume num estado de equilíbrio inicial --- P e V representam a pressão e o volume num estado de equilíbrio final.

R- B

03-

a) É claro que se você misturar 10g de álcool com 1000L=1000kg=10⁶g de água, praticamente não haverá alteração na temperatura da água que continuará 33^oC, conforme resolução a seguir:

Quantidade de calor cedido pelo álcool --- Q_al=m_al.c_al.(t_e – t_o)=10.0,6.(t_e – 70) --- Q_al=6t_e – 420.

Quantidade de calor recebido pela água --- Q_ag=m_ag.c_ag.(t_e – t_o)=10⁶.1.(t_e – 33) --- Q_ag= 10⁶t_e – 33.10⁶.

Supondo que eles troquem calor apenas entre si --- Q_al = Q_ag --- 6t_e – 420 = 10⁶t_e – 33.10⁶ --- 10⁶t_e – 6t_e = 33.10⁶ – 420 --- t_e≈33.10⁶/10⁶ --- t_e≈33^oC.

A quantidade de calor que a água recebe é, em módulo, a mesma que o álcool cede e vale --- Q_al=6.(33 – 70) --- Q_al= - 222 cal --- (o sinal negativo significa apenas que o álcool está cedendo calor à água) --- assim, a água recebe Q_ag=222 cal.

b) A entropia do reservatório de água é dada por --- ΔS_ag =Q_ag/T=222/(33 + 273)=222/306 --- ΔS_ag=0,73ca/K.

O enunciado fornece que a variação de entropia do sistema (reservatório de água e a gota de álcool) é ΔS_sistema ≥ 0 ---ΔS_sistema = ΔS_ag +ΔSal ≥ 0.

Como a gota de álcool está cedendo calor, sua variação de entropia será negativa.

Assim, a variação de entropia da gota de álcool vale ΔS_al ≥ −0, 73cal/H.

04-

C/5 = (87,8 – 32)/9 --- C/5 = 55,8/9 --- 9C=279 --- C=31oC.

R- B

05- I. Correta --- em Florianópolis a água ferve a 100^oC e em Lages, a 97^oC e, assim, em Florianópolis ficam, no mesmo tempo que em Lages, a uma temperatura maior.

II. Correta --- a temperatura de ebulição está relacionada com a pressão --- maior pressão, maior temperatura de ebulição.

III. Correta --- Veja (II)

IV. Falsa --- a panela de pressão aumenta a pressão interna fazendo com que a temperatura de ebulição fique maior que 100^oC, e deve ser usada em Lages onde a temperatura de ebulição é menor.

R- A

06- Observe no gráfico que, quando C=0^oC, X=25^oX e que, quando C=10^oC, X=85^oX.

Equação de conversão:

Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de acordo com a relação matemática baseada no teorema de Thales:

Calor específico (sensível da liga metálica --- C_l=0,1cal/(g.^oX) --- observe que, para cada variação de 10^oC (10 – 0) na Celsius, ocorre uma variação de 60^oX (85 – 25) na escala X.

Regra de três:

Portanto c_l = 0,1^o g/(cal.^oX)=0,1 cal/g.(1/6)^oC --- c_l=0,6 cal/g^oC

Q_a + Q_l = 0 --- 100t – 2000 + 120t – 9000 = 0 --- t=11000/220 --- t=50^oC.

07- Pelo enunciado, durante o processo de varredura ocorre a formação de uma película de água líquida entre a pedra e a pista, ou seja, está havendo uma fusão, uma passagem do estado sólido para o líquido.

Assim, a transformação promovida pela varredura é a de número 1.

08- Após a queima de 4,00g de carvão, a temperatura interna do calorímetro aumentou de Δθ=(31,3 – 20,0)=11,3^oC.

Capacidade térmica=variação da quantidade de calor/variação da temperatura --- C=ΔQ/Δθ ---

21,4=ΔQ/11,3 --- ΔQ=241,82kcal.

O exercício pede a quantidade de calor, em kcal/g (kcal por cada grama), liberada na queima do carvão --- regra de três --- 4g – 241,82kcal --- 1g – Q --- 4Q=241,82 --- Q=60,45kcal.

R- E

09- Nas regiões desérticas a amplitude térmica (diferença entre a máxima e mínima temperaturas) é bastante elevada e nas regiões litorâneas ela é bem menor devido ao alto calor específico da água em relação a outras substâncias, é que ela pode absorver ou ceder grandes quantidades de calor

com pequena alteração de temperatura. Isto ocorre devido às pontes de hidrogênio que mantêm as moléculas unidas. Nas regiões desérticas a ausência de água faz um ambiente possuir um baixo calor específico, e desta forma o ambiente se aquece facilmente e se arrefece facilmente.

R- B

10- Lâminas bimetálicas – Quando você solda duas barras de materiais diferentes você obtém uma lâmina bimetálica e, se você as submeter à mesma variação de temperatura, o sistema vai curvar-se para o lado da barra de menor coeficiente de dilatação (se dilata menos, ferro), quando aquecida e para o lado da barra de maior coeficiente de dilatação (se dilata menos, bronze), quando resfriada, pois ∆L=L_o.α.∆Ɵ e, nesta expressão a dilatação ∆L é diretamente proporcional ao coeficiente de dilatação α --- R- D

11- Cálculo da energia liberada numa queda livre pelas duas massas de m_total=6 + 4=10kg caindo de uma altura de h=2m --- como caem com velocidade constante não existe variação de energia cinética, apenas de energia potencial gravitacional --- assim, a energia mecânica passou de E_mi=mgh=10.10.2=200J para E_mf=mgh=10.10.0=0 --- ΔE_m=200 – 0=200J --- para 40 quedas ---ΔE_m=40.200=8000J --- pelo enunciado toda essa energia foi utilizada no aquecimento de m=1kg =1000g de água, de calor específico c=4,0J/g^oC produzindo um aquecimento ΔӨ de --- ΔE_m = Q=mc ΔӨ --- 8000 = 10³.4.ΔӨ --- ΔӨ=8000/4000 --- ΔӨ = 2^oC.

12- Pelo enunciado as temperaturas final e inicial são iguais, portanto trata-se de uma transformação isotérmica (mesma temperatura T) onde P.V=constante. Observe nessa expressão que, depois de aberta a válvula o gás dobra seu volume e, para que o produto PxV seja constante a pressão anterior P₁ deve cair pela metade --- R- A

13- Se você não domina a teoria, ela está a seguir:

Capacidade térmica (C)

Define-se capacidade térmica (C) ou capacidade calorífica de um corpo como sendo o produto da massa desse corpo pelo calor específico da substância de que ele é constituído, ou seja, --- C=m.c --- como Q=m.c.Δt --- Q=C.Δt --- ou Q=C/(t – t_o)

Se, por exemplo, a capacidade térmica de um corpo é C=40cal/^oC, isto significa que, quando esse corpo receber ou ceder 40 calorias, sua temperatura aumentará ou diminuirá de 1 ^oC.

Princípio das trocas de calor

Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico. Assim , como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes é igual à quantidade de calor recebida pelos mais frios:

Princípio da Conservação da energia.

Como a quantidade de calor recebida é positiva e a cedida é negativa, tem-se que --- Q₁ + Q₂ + Q₃ + ....+ Q_N= 0 ou m₁.c₁.(t – t_o1) + m₂.c₂.(t – t_o2) + m₃.c₃.(t – t_o3) + … + m_N.c_N.(t – t_oN) = 0

No exercício:

Esfera metálica --- t_o=50^oC --- C=mc=2cal/^oC --- t_equilíbrio=?

Água --- t_o=30^oC --- C=mc=2000cal/^oC --- t_equilíbrio=?

m_a.c_a.(t_equilíbrio – t_o) + m_e.c_e.(t_equilíbrio – t_o)=0 --- C_a.(t_equilíbrio – t_o) + C_e.(t_equilíbrio – t_o)=0 --- 2000.(t_equilíbrio – 30) + 2.(t_equilíbrio – 50)=0 --- 2000.t_equilíbrio – 60000 + 2.t_equilíbrio – 100=0 --- 2002.t_equilíbrio = 60100 ---

t_equilíbrio=60100/2002=30,01^oC

R- B

14-

Relação entre as escalas

Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de acordo com a relação matemática baseada no teorema de Thales:

C/5 =K – (273)/5 --- C=K – 273=313 – 273 --- C=40^oC

R- C

15- A teoria é fornecida a seguir:

Denomina-se calor sensível ou calor específico (c) o calor que provoca uma variação na temperatura de um corpo, sem que ele mude de estado físico.

Verifica-se experimentalmente que a quantidade de calor (Q) recebida ou cedida por um corpo é diretamente proporcional à sua massa e á sua variação de temperatura.

Matematicamente:

Onde c é o calor especifico (constante de proporcionalidade que é característica de cada corpo).

Características do calor específico:

Substituindo m=1g e Δt=1 ^oC na expressão Q=m.c.Δt --- Q=1.c.1 --- Q=c --- ou seja, o calor específico de uma substância é a quantidade de calor necessária para fazer a temperatura da massa de 1g ou 1kg dessa substância sofrer uma variação de temperatura de 1 ^oC.

Quando se afirma que o calor específico do álcool é 2400 J/(kg·ºC), quer-se dizer que, para uma massa de 1kg de álcool sofrer uma variação de temperatura de 1 ^oC, ela deve receber ou ceder,

2 400J de energia.

R- B

16-

R- A

17-

Relação entre as escalas termométricas

Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de acordo com a relação matemática baseada no teorema de Thales:

18- Isobárico, pressão constante --- P=P_o --- P_o.V_o/T_o=P.V/T --- P.V_o/T_o=P.V/T --- V_o/T_o=V/T ---

V_o/473=V/673 --- V/V_o=673/473= 1,4 --- R- C

19- Relação entre os coeficientes de dilatação linear (α), superficial (β) e volumétrico (λ) --- α/1= β/2 = λ/3 --- Β=2α e λ=3α ---chapa fina de lados L_o--- S_o=L_o.L_o=L_o² --- dilatação com variação de temperatura

ΔT --- ΔS=S_o.β.ΔT --- ΔS=S_o.2α.ΔT (I) --- dilatação com variação de temperatura 2ΔT --- ΔS’=S_o.β.2ΔT --- ΔS’=L_o².2α.2ΔT --- ΔS’=4L_o².α.ΔT (II) --- (I)/(II) --- ΔS’/ΔS=4L_o².α.ΔT / L_o².2α.ΔT --- ΔS’/ΔS=2 ---

--- cubo metálico de lados L_o--- V_o=L_o.L_o.L_o==L_o³ --- dilatação com variação de temperatura ΔT ---

ΔV=V_o.λ.ΔT --- ΔV=L_o³.3α.ΔT (I) --- dilatação com variação de temperatura 2ΔT --- ΔV’=V_o.λ.2ΔT --- ΔV’=L_o³.3α.2ΔT --- ΔV’=6L_o³.α.ΔT (II) --- (I)/(II) --- ΔV’/ΔV=6L_o³.α.ΔT / L_o³.3α.ΔT --- ΔV’’/ΔV=2 ---

R- B

20- Inversão térmica – ocorre quando as camadas de ar próximas à superfície da Terra, que deveriam ser mais quentes para poderem se expandir e levar os poluentes, ficam mais frias (daí o nome de inversão térmica).

Assim, o ar frio fica retido na superfície, aprisionado pelo ar quente, impedindo as correntes de convecção, pois o ar frio que fica em baixo é mais denso e mais pesado e encontra dificuldades para subir, o que retém os poluentes próximos à superfície. Essa poluição provoca problemas de saúde como bronquite, pneumonia, asma, cansaço, etc. que atingem os indivíduos mais frágeis como idosos, crianças e doentes

R- E

21- A fusão ocorre à temperatura constante de θ=40^oC.

Quantidade de calor recebido no estado líquido --- Q=3minx2.10³ =6.10³J --- Q=m.c.Δθ --- 6.10³=

1.c.(70 – 40) --- c=6.10³/30 --- c=0,2.10³=200J/(kgK) --- lembre-se de que cada variação de 1 grau na escala Celsius corresponde a variação e 1 grau na escala Kelvin.

R- E

22- W=0,1kJ --- Quantidade de calor recebido no estado sólido --- Q=3minx2.10³ =6.10³J=6kJ --- segunda lei da termodinâmica --- ΔU = Q – W = 6kJ – 0,1kJ=5,9kJ.

R- B

23-

b) Cálculo do trabalho W_AB recebido (trata-se de uma compressão, volume do gás diminuindo) pelo gás entre os estados A e B --- esse trabalho é fornecido pela área entre A e B:

Cálculo da variação de energia interna no trecho AB (ΔU_AB) pela aplicação do primeiro princípio da termodinâmica:

Cálculo do trabalho W_BC cedido (trata-se de uma expansão, volume do gás aumentando) pelo gás entre os estados B e C ---esse trabalho é fornecido pela área entre B e C:

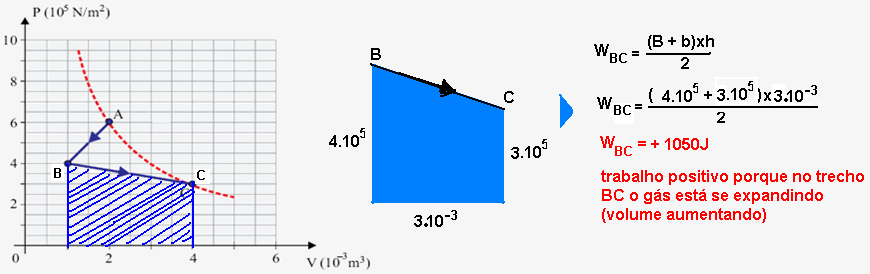
Cálculo da variação de energia interna no trecho BC --- em toda transformação cíclica a variação de energia interna é nula ( a temperatura final coincide com a temperatura inicial) e, assim ΔU_AB + ΔU_BC + ΔU_CA = 0 --- -300 + + ΔU_BC + + ΔU_CA = 0 --- mas ΔU_CA=0 (A e C estão à mesma temperatura, mesma isoterma) --- -300 + ΔU_BC + 0 = 0 --- ΔU_BC=300J

24- O Primeiro Princípio da Termodinâmica (Princípio da Conservação da Energia) afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”

Suponha que um sistema isolado receba Q= 300J de calor. Se, por exemplo, ΔU=50J dessa energia forem absorvidos pelo sistema, então a parte restante, W=250J, será fornecida ao ambiente sob a forma de trabalho.

Então, Q= W + ΔU ou,

A expressão acima é a representação matemática do primeiro princípio da termodinâmica.

O exercício quer a variação de energia interna (ΔU) do gás entre os estados 1 e 2 em que a transformação é isobárica (pressão constante de P=1,2.10⁵ Pa e o volume varia de V₁ = 0,008 m³ a V₂ = 0,012 m³ ---

Cálculo do trabalho W realizado nessa transformação onde, numa transformação isobárica é válida a relação W=P.ΔV=1,2.10⁵.(0,012 – 0,08)=1,2.10⁵x0,004 --- W=1,2.10⁵x4.10^-3 --- W=4,8.10²J=480J --- é fornecido que nesse trecho o gás recebe Q= 500J de calor:

Entre os estados 1 e 3:

25-

I. Correta

Máquina 1 --- temperatura da fonte fria em graus kelvin --- T_f=227 + 273=500K --- temperatura da fonte quente em graus kelvin --- T_q=527 + 73=800K --- o rendimento η de uma máquina de Carnot, em função da temperatura absoluta é fornecido por η₁= 1 – T_f/T_q = 1 – 500/800= 1 – 5/8=3/8 --- η₁=0,375=37,5% --- η₁=37,5% Máquina 2 --- temperatura da fonte fria em graus kelvin --- T_f=227K --- temperatura da fonte quente em graus kelvin --- T_q=527K --- o rendimento η de uma máquina de Carnot, em função da temperatura absoluta é fornecido por η₂= 1 – T_f/T_q = 1 – 227/527=0,57 --- η₂=57% ---

portanto η₂ > η₁

II. Falsa

É fornecido o trabalho realizado pela máquina 1 --- W=2000J --- rendimento da máquina 1, calculado em I --- η₁=0,375 --- deve-se determinar a quantidade de calor Q_q que a máquina recebe da fonte quente --- a expressão que relaciona essas grandezas é --- η₁=W/Q_q --- 0,375=2000/Q_q --- Q_q=2000/0,375≈5333,3J --- esse valor é diferente de 6000J.

III. Correta

É fornecido que a máquina 2 retirou 4000J da fonte quente --- Q_q=4000J --- rendimento da máquina 2 calculado em I --- η₂=0,57 --- η₂=W/Q_q --- 0,57=W/4000 --- W=2280J --- utilizando a relação a seguir --- Q_q= W + Q_f --- 4000=2280 + Q_f ---Q_f=1720J.

IV. Falsa

Observe na expressão η= 1 – Q_f/Q_q que, para uma mesma quantidade de calor retirada da fonte quente, ou seja, para um mesmo Q_q, o rendimento η e a quantidade de calor rejeitada para a fonte fria Q_f são inversamente proporcionais --- sendo η₂> η₁, Q_f2 será menor que Q_f1.

R- B.

26- Situação I. Transformação adiabática --- Nela, o sistema não troca calor com o meio externo (Q=0) --- ΔU=Q – W --- ΔU=0 – W --- ΔU= – W --- a variação de energia interna ΔU é igual ao módulo do trabalho termodinâmico W --- Situação II. Transformação isocórica, isométrica ou isovolumétrica --- ocorre a volume constante --- V_o=V --- ΔV=0 --- W=P.ΔV --- W=P.0 --- W=0 --- ΔU = Q – W ---

ΔU=Q – 0 --- ΔU=Q --- assim, todo o calor (Q) recebido (fluxo de calor) pelo sistema é igual à sua variação de energia interna (ΔU) ou à energia interna final do sistema --- R- C

27- Se você não domina o conteúdo, leia as informações abaixo: Pode-se definir o Segundo Princípio da Termodinâmica da seguinte maneira: “É impossível obter uma máquina térmica que, operando em ciclos, seja capaz de transformar totalmente o calor por ela recebido em trabalho”
Rendimento (η) de uma máquina térmica --- η=energia útil/energia total=W/Q --- exemplo: quando uma máquina térmica recebe, por exemplo, 300J de energia ou calor de uma fonte quente e só aproveita 150J desse calor na realização de trabalho (W), seu rendimento será --- η=W/Q=150/300=0,5x100 --- η=50%

Ciclo de Carnot

Carnot estabeleceu que: Se uma máquina térmica operar em ciclos entre duas fontes térmicas,

uma quente e outra fria, ela deve retirar calor (Q) da fonte quente, convertê-lo parcialmente em trabalho (W) e o restante (Q_r) rejeitar para a fonte fria. Exemplo: o motor de um carro é a fonte quente, local onde ocorre a queima do combustível, que fornece o calor. Dessa fonte térmica é retirada, a cada ciclo, uma quantidade de calor. Parte deste calor é convertida em trabalho mecânico útil (energia útil), fazendo o carro se mover. A outra parte do calor que não é aproveitada é rejeitada para a atmosfera, fonte fria, por meio do escapamento.

Como o rendimento de uma máquina térmica é sempre menor que 1 (η=W/Q, com W sempre menor que Q), Carnot demonstrou que, teoricamente, existe uma sequência específica de transformações na qual a máquina térmica obtém o máximo de rendimento. O ciclo no qual isso ocorre é denominado ciclo de Carnot e a máquina que opera segundo esse ciclo é chamada máquina de Carnot. Por ser ideal e imaginária, a máquina proposta por Carnot não contraria a segunda lei da Termodinâmica.

A seqüência do ciclo de Carnot cuja máquina térmica que o realiza é denominada máquina de Carnot:

Carnot demonstrou que o rendimento (η) de uma máquina térmica depende somente das temperaturas entre as quais ela trabalha ou que, no ciclo de Carnot, o rendimento é função exclusiva das temperaturas absolutas das fontes fria e quente e não depende da substância que faz a máquina térmica funcionar.

Carnot demonstrou que:

R- A

Termometria – medida de temperatura

36- a) Falsa --- C/5 = (F – 32)/9 --- quando eles indicarem valores iguais C=F=x --- x/5 = (x – 32)/9 --- 5x – 160 = 9x --- x=F=C= -40^oC (quando a Celsius indicar - 40^oC a Fahrenheit indicará também - 40^oF).

b) Falsa --- veja (a).

c) Correta --- ∆C/5 = ∆F/9 --- 5∆F=9∆C --- ∆F=1,8∆C --- a uma variação de 1o na escala Celsius corresponde uma variação de 1,8^o na escala Fahrenheit.

d) Falsa --- a altura da coluna líquida é a mesma para os dois termômetros, pois se trata do mesmo líquido e, portanto, para a mesma variação de temperatura sofrem a mesma dilatação volumétrica.

R- C.

37- Pode-se transformar uma indicação de uma escala para outra conforme o procedimento a seguir, de acordo com a relação matemática baseada no teorema de Thales:

No caso do exercício --- C/5 = (F – 32)/9 --- C/5 = (10,4 – 32)/9 --- C/5 = - 21,6/9 --- C=- 108/9= - 12^oC --- R- C

Propagação do calor

69- Leia abaixo o processo de transferência de calor por condução:

Condução térmica

O calor é conduzido de um ponto a outro do corpo sem que haja deslocamento das partículas.

Explicando microscopicamente o fenômeno: a região próxima da chama tem o movimento vibratório de suas moléculas aumentado, adquirindo assim maior energia cinética, que é transferida através de choques às partículas vizinhas, que também aumentam seu movimento vibratório. Através desse transporte de energia, toda a barra é aquecida, pois os metais são bons condutores de calor --- maneira que este tipo de cooler refrigera o processador segue um princípio bem simples: o calor gerado pelo processador é transferido devido à diferença de temperaturas entre eles, para o metal do cooler por condução, que ao mesmo tempo é resfriado pela corrente de ar trazida pela ventoinha, provocando nova transferência de calor do processador para o cooler e assim sucessivamente --- vale ressaltar que a condução de calor do processador para o metal é potencializada por uma pasta térmica especial para este tipo de situação.
R- C.

70-

I. Verdadeira --- O Efeito de Estufa consiste, basicamente, na ação do dióxido de carbono e outros gases sobre os raios infravermelhos refletidos pela superfície da terra, reenviando-os para ela, mantendo assim uma temperatura estável no planeta.

II. Verdadeira --- A radiação solar, em sua maioria aquela dentro da região visível do espectro eletromagnético, aquece o nosso planeta naturalmente (Fonte:Ministério da Ciência e Tecnologia).

III. Falsa --- Ao ser aquecida pela radiação solar, a superfície terrestre passa a emitir energia na forma de calor. Parte dessa energia se perde no espaço; o restante é absorvido por certos gases atmosféricos, presentes normalmente em quantidades muito pequenas. A energia absorvida é então irradiada de volta à superfície terrestre.

R- A.

71- 1^o --- Se o ASPS, região de alta pressão na atmosfera, funciona como uma “tampa” ele dificulta o movimento vertical do ar, inibindo, portanto, as correntes de convecção.

2^o --- De noite a Terra perde calor mais rapidamente devido à falta de nuvens e à pouca umidade da atmosfera na região do Atacama e essa falta de nuvens favorece a irradiação ou radiação do calor ---R- C.

72- a) A intensidade da radiação solar absorvida pela placa coletora é igual ao quociente entre a potência P da placa coletora e a área S da mesma --- I=P/S --- 400 = P/2 --- P=800W --- essa potência P=800W é definida como sendo à razão entre a energia W absorvida pelo coletor (no caso, térmica, calor) e o respectivo intervalo de tempo ∆t=1,0min=60s --- P=W/∆t --- 800 = W/60 --- W=Q=4.8000J=4,8.10⁴J --- equação fundamental da calorimetria --- Q=m.c.∆θ --- 4,8.10⁴=6,10³. ∆θ --- ∆θ=4,8.10⁴/6.10³ --- ∆θ=8,0^oC.

b) Dados --- T_o=290K --- T=300K --- ρ_o=1,2kg/m³ --- m (constante) --- P (constante) ---densidade=massa/volume --- ρ=m/V --- V=m/ρ --- V_o=m/ρ_o --- equação geral dos gases perfeitos --- P.V_o/T_o = P.V/T --- (m/ρ_o)/T_o=(m/ρ)/T --- ρ_o.T_o= ρ.T --- 1,2x290 =ρ.300 --- ρ=1,2x290/300=348/300 --- ρ=1,16kg/m³.

Termologia

Conceitos iniciais

22- A pressão no interior do botijão é elevada (bem superior à pressão atmosférica) --- devido a isto o gás no botijão está sob a forma líquida --- neste caso o combustível dentro do botijão é denominado Gás Liquefeito de Petróleo – GLP --- quando você abre o queimador a pressão passa a ser a pressão atmosférica, bem menos elevada e, nela, o GLP não pode existir sob a forma líquida: ele se transforma em gás (na forma gasosa) e escapa pelo queimador --- se surgir uma faísca elétrica o gás se inflama --- assim a transformação do líquido em gás não é causado pela chama: é causado pela queda da pressão. A chama foi causada pela fonte de calor Logo a afirmação C está errada --- R- B.

Calorimetria

Calor sensível (específico) e trocas de calor sem mudança de estado

73- Trata-se de uma mistura de 25L de água passando de 34º C para 30º C com um volume V de água passando de 18º C para 30º C --- mc(t – to) + mc(t – to)=0 --- 25.c.(30 – 45) + V.c.(30 – 18)=0 --- 12V=375 --- V=31,25L (volume recebido da torneira) --- volume total na banheira --- V’=31,25 + 25=36,25L --- tempo que a torneira demora para colocar 31,25L de água na banheira com vazão de 10L por minuto --- ∆t=31,25/10=3,125minx60=187,5s ---

R- C.

74- Supondo que não haja perdas de calor a quantidade de calor que um cede (negativa) é a mesma que o outro recebe (positiva), ou seja, Q₁+ Q₂ = 0 --- m.c₁.(t_f – t₁) + m.c₂.(t_f – t₂)=0 --- c₁.t_f – c₁.t₁ = c₂.t₂ – c₂.t_f --- t_f.(c₁ + c₂)=c₁.t₁ + c₂.t₂ --- t_f= (c₁.t₁ + c₂.t₂)/(c₁ + c₂) --- R- C.

75- Se você não domina a teoria, ela está detalhada a seguir:

Princípio das trocas de calor

Colocando vários corpos a diferentes temperaturas no interior de um recipiente adiabático, haverá trocas de calor entre eles, até atingirem o equilíbrio térmico.

Assim, como o recipiente é adiabático, a quantidade de calor cedida pelos corpos mais quentes é igual à quantidade de calor recebida pelos mais frios: Princípio da Conservação da energia.

Como a quantidade de calor recebida é positiva e a recebida é negativa, tem-se que --- Q1 + Q2 + Q3 + ....+ QN = 0 ou

M1.c1.(t – t01) + m2.c2.(t – t02) + m3.c3.(t – to3) + … + mN.cN.(t – t0N) = 0

Calorímetros - são recipientes adiabáticos onde se estuda as trocas de calor entre corpos que são colocados em seu

interior.

Normalmente utiliza-se o calorímetro para se medir o calor específico de um corpo de massa (mc), mergulhando-o no interior do calorímetro, onde se tem água de massa (ma), um termômetro e um agitador de líquido.

Aquece-se o corpo cujo calor específico você deseja determinar e o introduz na água do calorímetro. Agita-se o sistema, espera ser atingido o equilíbrio térmico (te) que é medida.

Conhecendo as temperaturas iniciais da água e do corpo e o calor específico da água, determina-se o calor específico (cc) do corpo pela expressão --- mc.cc.(te – toc) + ma.ca.(te – toa) = 0.

No caso do exercício, observe que o calorímetro e a massa de 100g de água a 2º C que já estavam em seu interior não vão influir nas trocas de calor já que as temperaturas inicial e final são iguais (20º C) --- assim, os 200g de água a 100º C devem passar para a água a 20º C quando misturados com uma massa m de água a 0o C, que também deve passar para 20º C --- Qcedido + Qrecebido=0 --- 200.1.(20 – 100) + m.1.(20 – 0) = 0 --- 16000 = 20m --- m=800g --- R- B.

76- Substituindo na expressão fornecida T(t) = (To – Tar).10 – t/12 + Tar, To=740º C, T(t)=140º C e Tar=40º C --- 140 = (740 – 40).10-t/12 + 40 --- 100=700x10-t/12 --- 1 = 7x10-t/12 --- 1/7 = 10-t/12 --- log(1/7) = log(10-t/12) --- log(7-1) = -(t/12). log10 --- -log(7) = - t/12 --- t=12.log(7) minutos --- R- C.

77- a) A intensidade da radiação solar absorvida pela placa coletora é igual ao quociente entre a potência P da placa coletora e a área S da mesma --- I=P/S --- 400 = P/2 --- P=800W --- essa potência P=800W é definida como sendo à razão entre a energia W absorvida pelo coletor (no caso, térmica, calor) e o respectivo intervalo de tempo ∆t=1,0min=60s --- P=W/∆t --- 800 = W/60 --- W=Q=4.8000J=4,8.10⁴J --- equação fundamental da calorimetria --- Q=m.c.∆θ --- 4,8.10⁴=6,10³. ∆θ --- ∆θ=4,8.104/6.103 --- ∆θ=8,0^oC.

b) Dados --- To=290K --- T=300K --- ρo=1,2kg/m3 --- m (constante) --- P (constante) ---densidade=massa/

volume --- ρ=m/V --- V=m/ρ --- Vo=m/ρo --- equação geral dos gases perfeitos --- P.Vo/To = P.V/T --- (m/ρo)/To=(m/ρ)/T --- ρo.To= ρ.T --- 1,2x290 =ρ.300 --- ρ=1,2x290/300=348/300 --- ρ=1,16kg/m³.

Calor Latente – trocas de calor com mudança de estado

57- Pelos dados você pode observar que no final haverá água líquida à temperatura t --- calor cedido por m=10g de gelo a -10oC até água a t --- Q1=m.cgelo.(t – to) + m.L + m.cágua.(t – to)=10.0,5.{0 – (-10)} + 10.80 + 10.1.(t -0) --- Q1=10t + 850 --- calor cedido por 90g de água para a 50oC até chegar a água a t --- Q2=mcágua.(t – to)=90.1.(t – 50) --- Q2=90t – 4500 --- Q1 + Q2=0 --- 10t + 850 + 90t – 4500 = 0 --- 100t=3650 --- t=36,50oC --- R-C.

58- De água a 20oC a água a 100oC --- não tem mudança de estado (calor sensível) --- Q1=m.c.(t – to) --- Q1=0,5.4.2.103(100 – 20) --- Q1=32.104J --- de água a 100oC a vapor a 100oC --- mudança de estado (calor latente) --- Q2=m.L ---Q2=0,5.2,26.106 --- Q2=1,13.106J --- Qtotal=32.104 + 113.104 =145.104=1,45.106J --- R- D.

59- Trata-se apenas de uma mudança de estado (fusão a 0oC) --- Q=m.LF=3.10.80=2400=2,4.103cal --- R- E.

60- De gelo a – 4oC a água a 0oC --- não tem mudança de estado --- Q1=m.csólido.(θ – θo)=100.0,5.[0 – (- 4)]=200 cal --- de gelo a 0oC a água a 0oC --- é uma mudança de estado (fusão) --- Q2=m.Lfusão=100.80=8000 cal --- de água a 0oC a água a 37oC --- não tem mudança de estado --- Q3= m.clíquido.(θ – θo) =100.1 (37 – 0)=3700 cal --- Qtotal=Q1 + Q2 + Q3=20 + 8000 + 3700 --- Qtotal=11900 cal=11,9 kcal --- R- D.

61- a) Observe pelo gráfico que no estado sólido, enquanto a temperatura do corpo sobe de OoC até 4oC o corpo absorve a quantidade de calor de Q1=400cal --- calor específico no estado sólido (cs) --- Q1=m.cs.(θ – θo) --- 400 =

100.cs.(40 – 0) --- cs=400/4000 --- cs=0,1caç/goC --- na fase líquida enquanto a temperatura do corpo sobe de 400C para 60oC são absorvidas Q2=(1200 – 800)=400cal --- Q2=m.cl. (θ – θo) --- 400=100.cl.(60 – 40) --- cl=400/2000 --- cl=0,2cal/goC.

b) A fusão ocorre quando a substância passa de sólido a 40oC para líquido a 40oC , assim sua temperatura de fusão é

40oC --- para se fundir ela recebe Q3=800 – 400=400cal --- calor latente de fusão --- Q3=mLf --- 400=100Lf --- Lf=4cal/g.

Dilatometria

Dilatação linear, superficial e volumétrica

78- 01. Correta --- equação fundamental da calorimetria --- Q=m.c.(t – to)=1.0,5.(50 – 20) ---Q=15kcal=15000cal --- Q=1,5.104cal.

02. Correta --- ∆ℓ = ℓo.α.(t – to)=0,5.2.10-6.(50 – 20) --- ∆ℓ = 30.10-6m=3.10-3cm.

04.Correta --- C=∆Q/∆t=15000/30 --- C=5.102=500cal/oC.

08- Falsa --- seria o dobro se o calor específico da barra fosse o dobro.

16. Falsa --- se o comprimento da barra aumenta, sua densidade linear deve diminuir (d=m/ℓ - d e ℓ são inversamente proporcionais)

R- (01. 02. 04)

79- Expressão da dilatação linear --- ∆L=Loα∆θ --- ∆L/∆θ=Loα --- sendo as duas retas paralelas a tangente do ângulo θ entre as duas é a mesma --- tgθ=∆LB/∆θ=∆LA/∆θ --- ∆LB = ∆LA --- LoB.αB = LoB.αB --- 2LαB = LαA --- αA/αB=2.

R- A.

Termodinâmica

Mudanças de estado físico

52- I. A água que está no estado líquido é resfriada até temperaturas abaixo de 0oC se congelando, ou seja, passando para o estado sólido --- seta 2 do gráfico --- II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada, ou seja, o gelo (estado sólido) passa para a fase de vapor --- seta 3 do gráfico --- R- C.

Transformações gasosas

52- a) Entre 1 e 2 trata-se de uma transformação isotérmica cujas características são fornecidas a seguir:

Nela, durante todo o processo, a temperatura permanece constante (isso=igual; thermos=temperatura) --- o cientista Robert Boyle comprovou que, quando a temperatura é constante, a pressão (P) exercida por certa massa gasosa é inversamente proporcional ao volume (V) por ela ocupado --- ou --- P.V=constante --- ou ainda --- Po.Vo=P.V --- P e Vo representam a pressão e o volume num estado de equilíbrio inicial --- P e V representam a pressão e o volume num estado de equilíbrio final.

Sendo P = k / V, se V tende a zero P cresce indefinidamente e se V cresce indefinidamente p tende a zero e, se você representar graficamente P x V você obterá uma curva de nome isoterma que é um ramo de uma hipérbole eqüilátera.

Cada ponto da curva (isoterma) A tem a mesma temperatura (TA); Cada ponto da curva (isoterma) B tem a mesma temperatura (TB) e cada ponto da curva (isoterma) C tem a mesma temperatura (TC).

Pelo gráfico são fornecidos --- P1=5.105Pa, V1=3.10-5m3, P2=3.105Pa e V2=? --- P1.V1=P2.V2 --- 5.105.3.10-5=3.105.

V2 --- V2=15.10-5/3 --- V2=5.10-5m3.

b) No trecho compreendido entre 2 e 3 ocorre uma transformação adiabática cuja expressão matemática é P.Vγ=constante, ou seja, P2.V2γ=P3.V3γ --- P3=P2.V2γ /V3γ --- substituindo os respectivos valores --- P3=3.105.

(5.10-5/6.10-5) 3/2 = 3.105.√53/63) --- P3=3.105.√0,58=3.105.0,77 --- P3≈2,3.105Pa.

53- São fornecidos --- P2/P1=0,26 --- P2=0,26P1 --- T1/T2≈1,3 --- T1≈1,3T2 --- substituindo esses valores na equação fornecida P1/T1μ1=P2/T2μ2 --- P1/1,3T2μ1=0,26P1/T2μ2 --- (1/1,3)μ1=0,26/μ2 --- μ2=0,338μ1 --- μ2/μ1=0,338≈0,34 -- R- E.

54- I. A água que está no estado líquido é resfriada até temperaturas abaixo de 0oC se congelando, ou seja, passando para o estado sólido --- seta 2 do gráfico --- II. Em câmaras especiais, sob baixíssima pressão (menores do que 0,006 atm), a temperatura do alimento é elevada, fazendo com que a água sólida seja sublimada, ou seja, o gelo (estado sólido) passa para a fase de vapor --- seta 3 do gráfico --- R- C.

Trabalho de um gás – transformação cíclica

27- Toda transformação cíclica deve obedecer às seguintes condições:

Como as temperaturas final e inicial são coincidentes (Ti=Tf), a variação de energia interna (ΔU) é nula --- ΔU=0

ΔU=Q – W --- 0=Q – W --- Qciclo=Wciclo (a quantidade de calor trocada com o meio externo é igual ao trabalho realizado na transformação)

Em toda transformação cíclica representada no diagrama PxV, o trabalho realizado é fornecido pela área do ciclo.

Se o ciclo é realizado no sentido horário, o trabalho é positivo.

Se o ciclo é realizado no sentido anti-horário, o trabalho é negativo.

O trabalho realizado é obtido pela área do ciclo (triângulo) --- W=bxh/2=(10 – 2).(10 – 2)/2=64/2=32J (positivo-ciclo no sentido horário) --- R- C.

28- Na expansão AB o trabalho realizado é fornecido por W=P.∆V=P.(VB – VA)=4.105.(1 – 0,3)=2,8.105 J --- WAB= =2,8.105J --- sendo a transformação ABCDA cíclica, as temperaturas final e inicial são as mesmas e, portanto, não há variação de energia interna ∆Utotal=0 --- ∆Utotal=∆UAB + ∆UBC + ∆UCD + ∆UDA=0 (I) --- primeiro princípio da termodinâmica no trecho AB --- ∆UAB=QAB– WAB --- QAB=400kJ=4.105J (dado) --- ∆UAB=4.105 – 2,8.105 --- ∆UAB=1,2.105J --- ∆UBC=0 (isotérmica) --- primeiro princípio da termodinâmica no trecho CD --- ∆UCD=QCD – WCD --- QCD= - 440kJ= - 4,4.105J (negativo, pelo enunciado perdeu calor para o meio externo) --- WCD=P.(VD - VC)=2.105.(0,5 – 2) --- WCD= - 3.105J --- ∆UCD=QCD – WCD= - 4,4.105 – (-3.105)= - 1,4.105J --- substituindo as energias internas em (I) --- 1,2.105 + 0 – 1,4.105 + ∆UDA = 0 --- ∆UDA=0,2.105=2.104J.

29- Toda transformação cíclica deve obedecer às seguintes condições:

Como as temperaturas final e inicial são coincidentes (Ti=Tf), a variação de energia interna (ΔU) é nula --- ΔU=0

ΔU=Q – W --- 0=Q – W --- Qciclo=Wciclo (a quantidade de calor trocada com o meio externo é igual ao trabalho realizado na transformação)

Em toda transformação cíclica representada no diagrama PxV, o trabalho realizado é fornecido pela área do ciclo.

Se o ciclo é realizado no sentido horário, o trabalho é positivo.

Se o ciclo é realizado no sentido anti-horário, o trabalho é negativo.

O trabalho realizado é obtido pela área do ciclo (triângulo) --- W=bxh/2=(10 – 2).(10 – 2)/2=64/2=32J (positivo-ciclo no sentido horário) --- R- C.

Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia

58- Trata-se do Primeiro Princípio da Termodinâmica ou Princípio da Conservação da energia que afirma que: “A energia não pode ser criada nem destruída, mas apenas transformada”

Suponha que um sistema isolado receba 300J de calor. Se, por exemplo, 50J dessa energia forem absorvidos pelo sistema, então a parte restante, 250J, será fornecida ao ambiente sob a forma de trabalho.

Então, Q= W + ΔU ou,

A expressão acima é a representação matemática do primeiro princípio da termodinâmica.

R- C.

59- Na expansão AB o trabalho realizado é fornecido por W=P.∆V=P.(VB – VA)=4.105.(1 – 0,3)=2,8.105 J --- WAB= =2,8.105J --- sendo a transformação ABCDA cíclica, as temperaturas final e inicial são as mesmas e, portanto, não há variação de energia interna ∆Utotal=0 --- ∆Utotal=∆UAB + ∆UBC + ∆UCD + ∆UDA=0 (I) --- primeiro princípio da termodinâmica no trecho AB --- ∆UAB=QAB– WAB --- QAB=400kJ=4.105J (dado) --- ∆UAB=4.105 – 2,8.105 --- ∆UAB=1,2.105J --- ∆UBC=0 (isotérmica) --- primeiro princípio da termodinâmica no trecho CD --- ∆UCD=QCD – WCD --- QCD= - 440kJ= - 4,4.105J (negativo, pelo enunciado perdeu calor para o meio externo) --- WCD=P.(VD - VC)=2.105.(0,5 – 2) --- WCD= - 3.105J --- ∆UCD=QCD – WCD= - 4,4.105 – (-3.105)= - 1,4.105J --- substituindo as energias internas em (I)

Segunda lei da Termodinâmica

49- O motor de um carro é a fonte quente, local onde ocorre a queima do combustível, que fornece o calor. Dessa fonte térmica é retirada, a cada ciclo, uma quantidade de calor. Parte deste calor é convertida em trabalho mecânico útil (energia útil), fazendo o carro se mover. A outra parte do calor que não é aproveitada é rejeitada para a atmosfera, fonte fria, por meio do escapamento --- o fator que limita a busca pela eficiência total de um motor é a segunda lei da Termodinâmica ao afirmar que o rendimento de uma máquina térmica é sempre menor que 1 (100%), impedindo que a transformação de calor em trabalho seja integral.

R- B.

50- Todas são falsas --- veja fisicaevestibular.com.br --- Física Térmica – Segundo Princípio da Termodinâmica --- R- C.

51-

Resumo da teoria do ciclo de Carnot:

Carnot demonstrou que:

Dados --- trabalho útil --- W=3200J --- W=Q – Q1 --- 3200= Q – Q1 --- Q1= Q – 3200 (I) --- temperatura da fonte fria --- T1=77 + 273=350K --- temperatura da fonte quente --- T= 427 + 273 =700K --- η = 1 – T1/T --- η = 1 – 350/700 --- η = 1 – 1/2 --- η = 1/2=0,5x100=50% --- η = 1 – Q1/Q (II) --- (I) em (II) --- 1/2 = 1 – (Q – 3200)/Q --- 1/2 = (Q – 3200)/Q --- Q = 2Q – 6400 --- Q=6400J (quantidade de calor recebido da fonte quente) --- Q1=3200J (quantidade de calor rejeitado para a fonte fria) --- R- B.