VR – Óptica

Vestibulares recentes por assunto – 2017 – 2016 - 2015

Princípios da propagação retilínea da luz

01-(UFLA – MG – PAS – 017/019)

Na terça-feira, 12 de abril de 2016, o físico Stephen Hawking anunciou que, em parceria com os empresários Mark Zuckerberg, criador do Facebook, e o bilionário russo Yuri Milner, sondas serão enviadas para Alpha Centauri, que é o astro mais brilhante da constelação de Centauro e a terceira estrela mais brilhante do céu visto a olho nu aqui da Terra. A ideia faz parte

Starshot, que desenvolverá nanosondas minúsculas e as enviará para o espaço usando raios de luz, impulsionando-as a 20% da velocidade da luz.

O sistema de Alpha Centauri fica a 4,4 anos-luz de distância da Terra. “Se for bem-sucedida, a missão pode chegar a Alpha Centauri cerca de X anos após seu lançamento”, afirmou Hawking. Calcule o tempo X que a sonda demorará para chegar à estrela Alpha Centauri.

Considere a velocidade da luz 3×10⁸ m/s.

02-(CEDERJ-RJ-2017)

Uma câmara escura é construída com uma caixinha cúbica de aresta L = 8 cm, à prova de luz, contendo um pequeno orifício circular em uma de suas faces. A luz de uma cena passa através do orifício e projeta uma imagem que é registrada em um filme fotográfico colado na face oposta àquela que contém o orifício. Suponha que um objeto de altura A = 2 mseja posicionado a uma distância D = 4 m do orifício da câmara escura, que o raio do orifício seja muito menor do que L e que a imagem registre completamente o objeto. Nesse caso, a altura da imagem registrada no filme será:

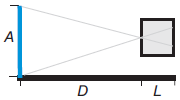
(A) 2 cm

(B) 4 cm

(C) 6 cm

(D) 8 cm

03-(PUC-SP-017)

Reflexão da luz e espelhos planos

04-(Faculdade de Medicina do Hospital Israelita Albert Einstein)

05-(UFJF-MG-017)

Espelhos esféricos

06-(UFPR-PR-017)

Um espelho côncavo com raio de curvatura 10 cm e centro em C, foi posicionado de acordo com a figura a seguir.

Um objeto O, com 2 cm de altura, está localizado a 3 cm do espelho eorientado para baixo, a partir do eixo principal.

Os segmentos que podem ser observados sobre o eixo principal são equidistantes entre si.

a) Na figura, assinale o foco do espelho, ressaltando-o por meio da letra F.

b) Determine, graficamente na figura, a imagem formada, representando adequadamente no mínimo dois raios “notáveis”, antes e após a ocorrência da reflexão.

c) Determine, apresentando os devidos cálculos, o tamanho da imagem.

07-(UNIMONTES – MG – 017 – PAES 2^a etapa)

08-(FATEC – SP – 16/17)

A malha ferroviária europeia é uma das mais antigas e extensas do mundo, com cerca de 260 mil quilômetros. Apesar de toda tecnologia moderna de segurança implantada em toda rede, as companhias ferroviárias ainda adotam um sistema básico de reflexão luminosa nas plataformas. Um espelho é colocado no ponto exato onde o operador (maquinista) para a composição, de modo que ele possa verificar se todos os passageiros embarcaram e desembarcaram. A fim de tornar isso possível, o espelho deve refletir um amplo ângulo de visão, ou seja, maior campo visual.

Para que isso aconteça, as companhias devem utilizar um espelho

(A) plano, com a mesma altura do vagão.

(B) convexo, com um valor alto de vergência em módulo.

(C) côncavo, cuja vergência possui um valor baixo em módulo.

(D) convergente, cuja vergência possui um valor alto e negativo.

(E) divergente, cuja vergência possui um valor alto e positivo.

09-(UNICAMP-SP-017)

10-(FMABC-SP-017)

11-(FAMERP-SP-017)

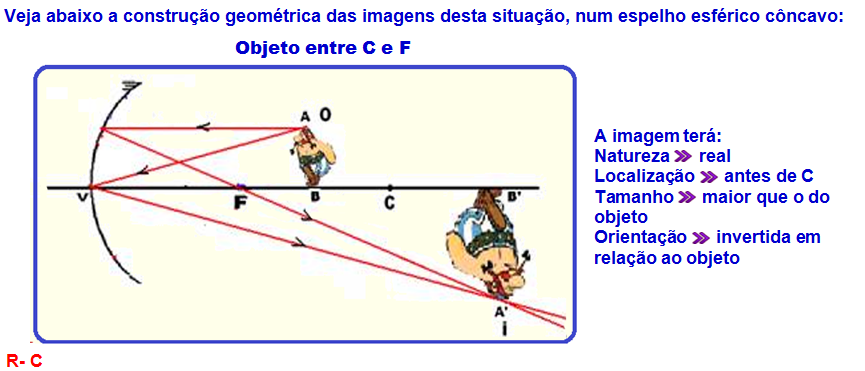
Uma calota esférica é refletora em ambas as faces, constituindo, aomesmo tempo, um espelho côncavo e um espelho convexo, de mesma distância focal, em módulo.

A figura 1 representa uma pessoa diante da face côncava e sua respectiva imagem, e a figura 2 representa a mesma pessoa diante da face convexa e sua respectiva imagem.

a) Considerando as informações contidas na figura 1, calcule o módulo da distância focal desses espelhos.

b) Na situação da figura 2, calcule o aumento linear transversal produzido pela face convexa da calota.

12-(Faculdade de Tecnologia Termomecânica – SP) 

Analise a figura.

(http://dornsife.usc.edu)

Com relação ao espelho e à imagem da mão, é correto afirmar que eles são, respectivamente,

(A) côncavo e real.

(B) côncavo e virtual.

(C) convexo e real.

(D) convexo e virtual.

(E) plano e real.

13-(UERJ-RJ/017)

Em uma aula prática de óptica, um espelho esférico côncavo é utilizado para obter a imagem de um

prédio.

Considere as seguintes medidas:

• altura do prédio = 20 m;

• distância do prédio ao espelho = 100 m;

• distância focal do espelho = 20 cm.

Admitindo que a imagem conjugada se situe no plano focal do espelho, calcule, em centímetros, a altura dessa imagem.

Refração luminosa

14-(Medicina – EMESCAM – ES – 017)

15-(IFMG-MG-2017)

Em um experimento de óptica, o professor Rafael faz com que um raio de luz monocromático

incida da maneira representa ao lado. O raio de luz forma um ângulo de 90° com a superfície da água.

O raio luminoso inicialmente viajava no ar e passa a viajar na água.Acerca deste experimento, é CORRETO afirmar que:

A) a luz não sofreu refração.

B) o ângulo de incidência vale 90°.

C) a frequência da luz sofreu alteração.

D) o comprimento de onda da luz sofreu alteração.

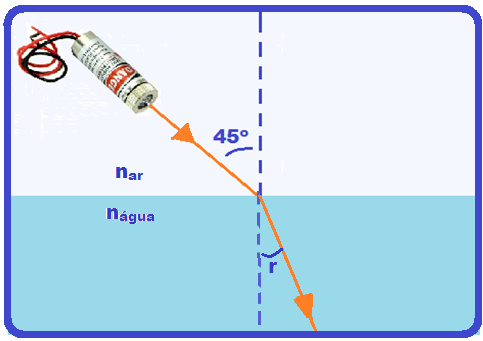
16-(PUC-RJ/017)

Um feixe luminoso proveniente de um laser se propaga no ar e incide sobre a superfície horizontal

da água fazendo um ângulo de 45^o com a vertical.

O ângulo que o feixe refratado forma com a vertical é:

Dados: Índice de refração do ar, 1,0; Índice de refração da água, 1,5;sen30^o = 1/2; sen45^o = /2 e sen60^o = /2.

(A) menor que 30º.

(B) maior que 30o e menor que 45^o.

(C) igual a 45^o.

(D) maior que 45^o e menor que 60^o.

(E) maior que 60^o.

17-(FMJ-SP-017)

As figuras representam raios de mesma luz monocromática que sofrem refração ao incidirem na superfície de separação de dois meios diferentes.

Os meios e seus respectivos índices de refração absolutos estão indicados na tabela.

Os meios A, B e C são, respectivamente,

(A) diamante, lantânio e vidro crown.

(B) vidro crown, lantânio e diamante.

(C) lantânio, vidro crown e diamante.

(D) vidro crown, diamante e lantânio.

(E) lantânio, diamante e vidro crown.

18-(UNIFESP-SP-017)

Para demonstrar o fenômeno da refração luminosa, um professor faz incidir um feixe monocromático de luz no ponto A da superfície lateral de um cilindro reto constituído de um material homogêneo e transparente, de índice de refração absoluto igual a 1,6 (figura 1).

A figura 2 representa a secção transversal circular desse cilindro, que contém o plano de incidência do feixe de luz.

Ao incidir no ponto A, o feixe atravessa o cilindro e emerge no ponto B, sofrendo um desvio angular α.

Sabendo que a velocidade da luz no vácuo é igual a 3.10 ⁸ m/s, que o índice de refração absoluto do ar é igual a 1,0 e adotando sen 53^o = 0,8, calcule:

a) a velocidade escalar do feixe luminoso, em m/s, no interior do cilindro.

b) o desvio angular α, em graus, sofrido pelo feixe luminoso ao atravessar o cilindro.

19-(Medicina – USCS-SP-017)

20-(EsPCEx- AMAN – SP- RJ – 2016/17)

21-(UNITAU MED-SP-017)

Uma onda luminosa propaga-se num meio A, onde sua velocidade é c/(20√3), e incide numa fronteira de separação com um meio B, formandoum ângulo de 60 graus com a normal. No meio B, a velocidade de propagação da luz passa a ser c/60.

Note que c é a velocidade da luz no vácuo, sendo c = 3 x 10⁵ km/s.

Dados: sen(60°) = √3/2 ; cos(60°) = 1/2 ; sen(30°) = 1/2 ; cos(30°) = √3/2

Admitindo a possibilidade da existência física e química desses meios, é CORRETO afirmar que o ângulo de refração dessa onda é de

a) 30 graus

b) 60 graus

c) 45 graus

d) 75 graus

e) 65 graus

Reflexão Total

22-(UNESP-SP-017)

Prismas

23-(FUVEST-SP-017)

Em uma aula de laboratório de física, utilizando-se o arranjo experimental esquematizado na figura, foi medido o índice de refração de um material sintético chamado poliestireno.

Nessa experiência, radiação eletromagnética, proveniente de um gerador de micro-ondas, propaga-se no ar e incide perpendicularmente em um dos lados de um bloco de poliestireno, cuja seção reta é um triângulo retângulo, que tem um dos ângulos medindo 25o, conforme a figura.

Um detector de micro-ondas indica que a radiação eletromagnética sai do bloco propagando-se no ar em uma direção que forma um ângulo de 15^o com a de incidência.

A partir desse resultado, conclui-se que o índice de refração do poliestireno em relação ao ar para essa micro-onda é, aproximadamente,

24-(FAMERP-SP-017)

Lentes

25-(UFES – ES – 017)

Com o sistema óptico ao lado, conseguem-se duas posições da lente delgada, P e P’, que produzirão imagens nítidas (focalizadas) do objeto sobre o anteparo.

A distância entre P e P’ é D = 6 cm, e a distância entre o objeto e o anteparo é mantida fixa no valor

L = 10 cm. Determine

A) se as imagens, nos dois casos, têm a mesma ampliação, ou seja, se têm o mesmo tamanho e explique seu raciocínio.

B) a distância entre o objeto e a lente na situação em que estão mais próximos entre si (posição P);

C) a distância focal da lente.

26-(FMJ-SP-017)

Leia o anúncio.

(www.importecnica.com.br. Adaptado.)

Considere que o “aumento de 5 vezes” signifique imagem direita e 5 vezes maior do que o objeto quando este se encontra a 20 cm da lente. A distância focal dessa lente é

(A) 100 cm.

(B) 25 cm.

(C) 10 cm.

(D) 17 cm.

(E) 20 cm.

27-(FGV-SP-017)

28-(UEMG-MG-017)

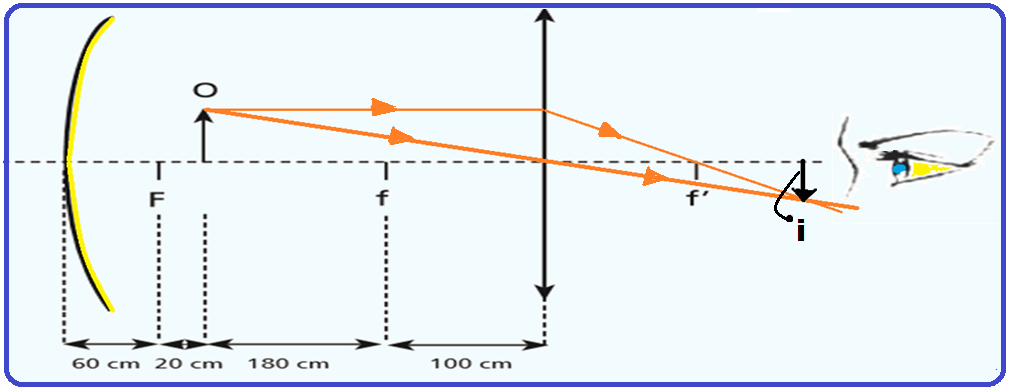
Um estudante dispunha de um espelho côncavo e de uma lente biconvexa de vidro para montar um dispositivo que amplia a imagem de um objeto.

Ele então montou o dispositivo, conforme mostrado no diagrama.

O foco do espelho é F e os das lentes são f e f’.

O objeto O é representado pela seta.

Após a montagem, o estudante observou que era possível visualizar duas imagens.

As características dessas imagens são:

a) Imagem 1: real, invertida e maior. Imagem 2: real, invertida e menor.

b) Imagem 1: real, direta e maior. Imagem 2: real, invertida e menor.

c) Imagem 1: virtual, direta e maior. Imagem 2: real, invertida e menor.

d) Imagem 1: virtual, direta e menor. Imagem 2: real, invertida e maior.

Instrumentos ópticos

29-(UNICAMP-SP-017)

Considere que, de forma simplificada, a resolução máxima de um microscópio óptico é igual ao comprimento de onda da luz incidente no objeto a ser observado.

Observando a célula representada na figura abaixo, e sabendo que o intervalo de frequências do

espectro de luz visível está compreendido entre 4,0.10¹⁴ Hz e 7,5.10¹⁴ Hz, a menor estrutura celular que se poderia observar nesse microscópio de luz seria (Se necessário, utilize c = 3.10⁸ m/s.)

Óptica Fisiológica

30-(COLÉGIO NAVAL – 2016/17)

Resoluções das questões de Vestibulares recentes por assunto – 2017 – 2016 – 2015 – Óptica

01- A velocidade das nanosondas corresponde a 20% da velocidade da luze terá valor  V = 20% de 3.10⁸ m/s  V = 0,2×3.10⁸ = 0,6.10⁸ m/s  V = 6.10⁷ m/s.

Um ano-luz é a distância que a luz pode viajar em um ano com velocidade de 3.108 m/s. Por exemplo, em um ano-luz, a distância percorrida seria de aproximadamente 9.460.800.000.000 (nove trilhões, quatrocentos e sessenta bilhões e oitocentos milhões) de quilômetros, ou, aproximadamente 9.1015 m.

V =  ∆S = 4,4×9.1015 = 39,6.1015 m  6.107 =   ∆t =  ∆t = 6,6.108 s.

Ano em segundos  1 minuto = 60 segundos  1 hora = 60 x 60 = 3600 segundos   1 dia = 24h x 3600 = 86.400 segundos  365 dias = 31.536.000 segundos  1 ano tem aproximadamente 3,15.107 s.

∆t =  21 anos

R- C

02-

Nós conseguimos resolver esse problema por semelhança de triângulos, observe a figura:

Os dois triângulos formados nessa figura são semelhantes, sendo assim:

O x é a altura da imagem, que será formada no fundo da câmera. Isolando ele:

Substituindo, o L está em cm (8 cm = 0,08 m) apenas dividir por 100:

Resolvendo:

x = 0,04 m = 4 cm

Alternativa B

03- Se você não domina a teoria, ela está a seguir:

Cor de um corpo

 A luz branca do Sol ou de uma lâmpada qualquer é denominada luz policromática (várias cores) e é composta das cores monocromáticas (uma só cor), vermelho, alaranjado, amarelo, verde, azul, anil e violeta.

A cor apresentada por um corpo, ao ser iluminado, depende do tipo de luz que ele reflete difusamente (espalha em todas as direções e sentidos) e que chega aos olhos do observador.

Um corpo negro absorve todas as cores e um corpo branco reflete todas as cores.

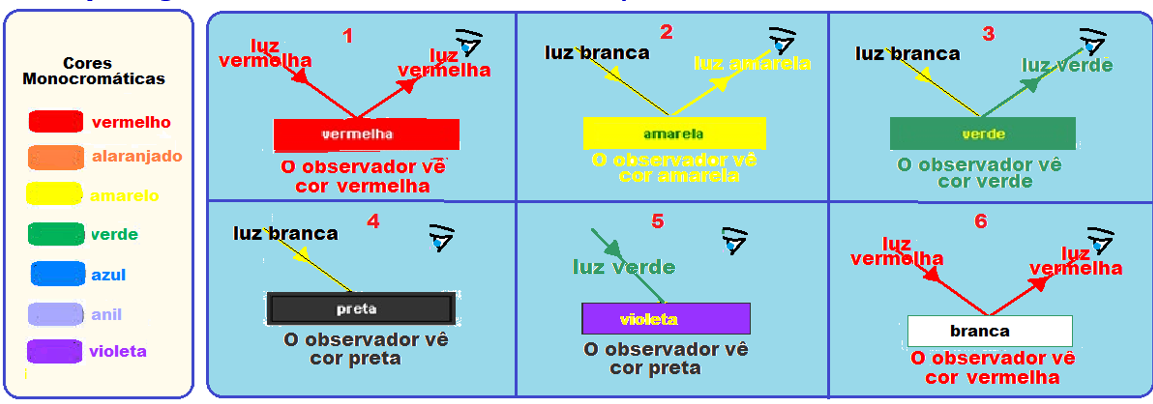
 Figura 1  O corpo vermelho reflete difusamente apenas a cor vermelha e o observador enxergará vermelho.

Figura 2  As sete cores (policromática branca) incidem sobre o corpo amarelo que reflete difusamente somente o amarelo e o observador enxergará essa cor.

Figura 3   As sete cores (policromática branca) incidem sobre o corpo verde que reflete difusamente somente o verde e o observador enxergará verde.

Figura 4  O corpo negro absorve todas as cores e nenhuma chegará ao observador que verá negro (ausência de cores).

Figura 5  O corpo violeta reflete difusamente somente o violeta e absorverá o verde, não chegando nenhuma luz ao observador, que verá negro.

Figura 6  O observador verá vermelho, pois o corpo branco reflete difusamente todas as cores inclusive o vermelho.

No caso do exercício, as palavras que você enxergará em azul são PRETO, VERDE e VERMELHO e as cores serão  azul (as três palavras anteriores) e preta (as demais radiações serão absorvidas fornecendo a sensação visual de preto).

R- B

04-

Características da imagem num espelho plano

O ponto objeto (O) e o ponto imagem (i) são simétricos em relação ao espelho, ou seja, a distância do

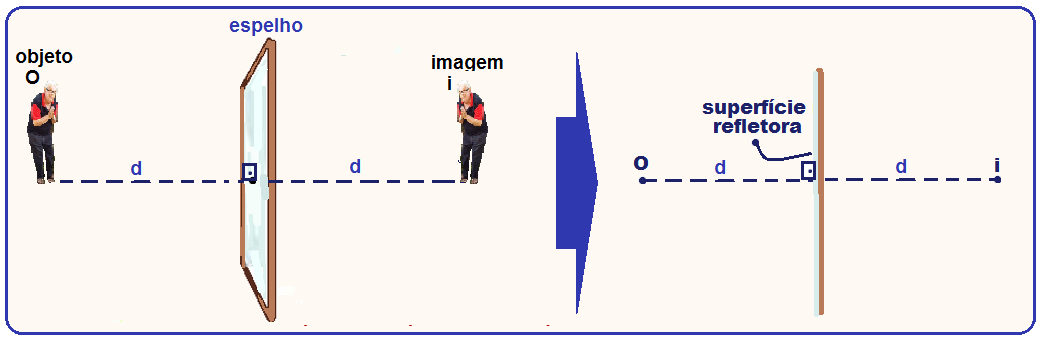
distância do objeto ao espelho é a mesma que a distância da imagem ao espelho e contidos numa mesma reta perpendicular ao plano do espelho.

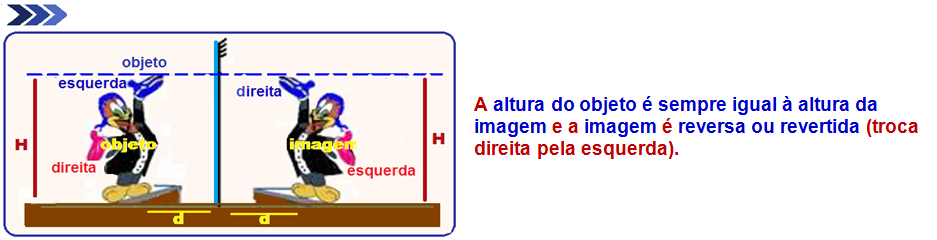
R- C

05-

06-

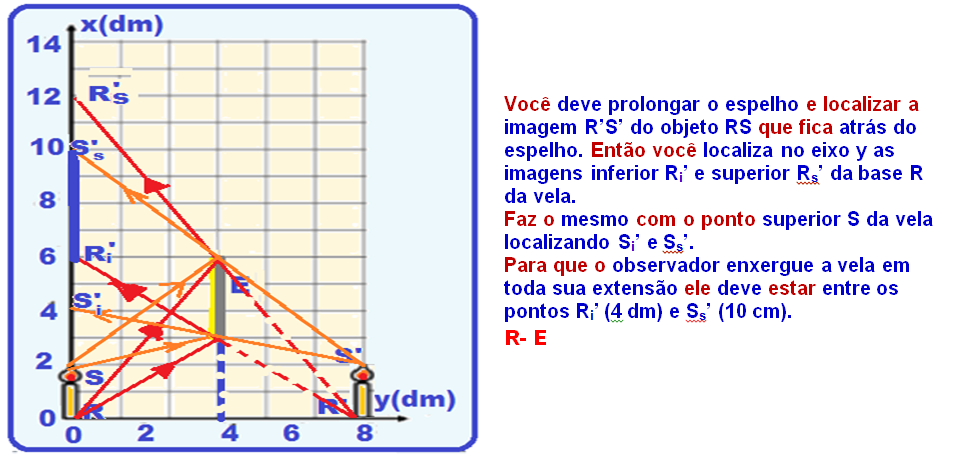
a) O foco F está localizado na distância média entre o centro de curvatura C e o espelho.

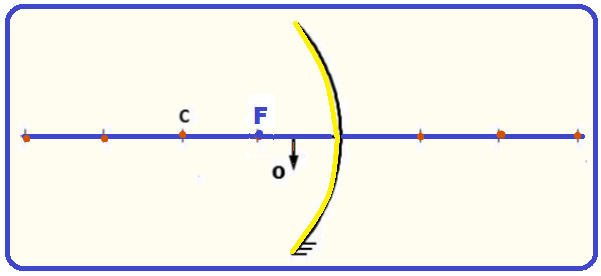
b)

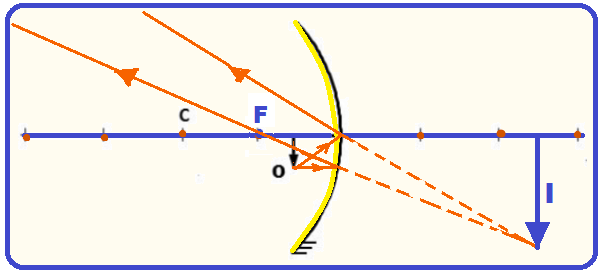
c)

f = R/2 = 10/2 = 5 cm (positivo, espelho côncavo).

P = 3 cm

P’ = ?

Equação dos pontos conjugados   =  +    =  +   -  =    =   P’ = – 7,5 cm (P’ < 0, imagem virtual)

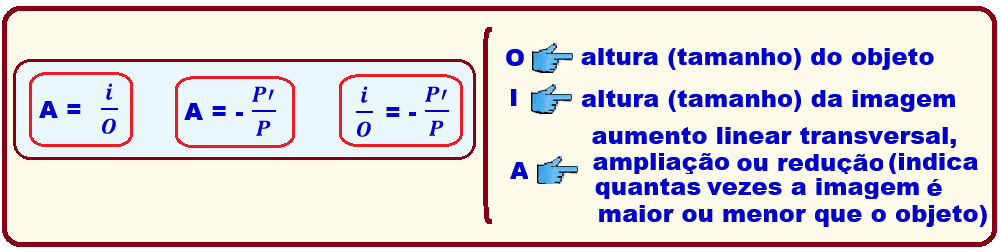
i= ?

o = - 2cm (invertida)

P = 3 cm

P’ = – 7,5 cm

 = –    = –   i =  = 5 cm ( a imagem é direita em relação ao objeto e tem 5cm de altura).

07-

08- Pelas características dos espelhos, podemos excluir algumas alternativas.

Por mais que um espelho plano ajudasse, ele não seria capaz de modificar a imagem, sendo assim não aumentaria seu campo de visão.

Um espelho côncavo converge os raios para um ponto, com isso não poderia ampliar o campo de visão do maquinista. Para um espelho ser considerado divergente ele precisa ter sua vergência negativa, quanto maior esse valor, em módulo, maior o campo de visão gerado.

Sendo assim, a alternativa B é a correta. Um espelho convexo aumenta o campo de visão, e se a vergência for grande mais expandido é esse campo visual.

R- B

09- O comportamento do balão de Natal como espelho é idêntico ao fornecido por um espelho esférico convexo, com as seguintes características:

Construção geométrica de imagens nos espelhos esféricos convexos

Espelho convexo  Para qualquer localização do objeto Independentemente de sua posição, a

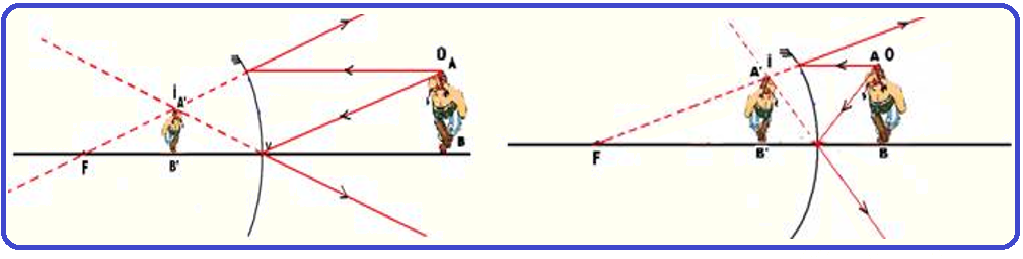
imagem terá sempre:

Natureza  virtual

Localização  atrás do espelho e entre V e F e observe nas figuras acima que à medida que o objeto se aproxima do espelho, a imagem também se aproxima e aumenta de tamanho, mas está sempre entre V e F.

Tamanho  menor que o do objeto

Orientação  direita em relação ao objeto

Utilidades: Os espelhos convexos são empregados como retrovisores em veículos, cabines de segurança, elevadores, etc.

Sua vantagem sobre o espelho plano, nesse particular, é ter maior campo visual. Têm, entretanto, o inconveniente de não darem noção da distância.

R- B

10-

11-

Na figura 1 a calota esférica está se comportando como um espelho esférico côncavo:

Módulo do espelho côncavo = módulo do espelho convexo = f = 30 cm.

b) Na figura 2 a calota esférica se comporta como um espelho esférico convexo de distância focal

f = – 30 cm (espelhos convexos possuem f < 0)

12-  Podemos excluir de imediato o espelho plano, pois nele não há como se modificar a imagem. Uma imagem formada por um espelho convexo deve ser, obrigatoriamente, virtual e menor que o objeto. Por a imagem ser expandida dessa forma, só podemos trabalhar com um espelho côncavo de modo que a imagem seja virtual, conforme esquema abaixo.

Objeto entre o foco F e o vértice V ou entre o foco F e o espelho

A imagem terá:

Natureza  virtual (obtida na interseção do prolongamento dos raios de luz )  não pode ser projetada, fotografada, etc., atrás do espelho.

Localização  atrás do espelho

Tamanho  maior que o do objeto

Orientação  direita em relação ao objeto

Utilidades: são empregados com frequência quando se deseja obter uma imagem virtual e ampliada de um objeto, como é o caso dos espelhos de barbear, toalete, de dentista, espelho de otorrinolaringologia, etc.

R- B

13-

Como o enunciado afirma que a imagem conjugada está situada no plano focal (f) do espelho 

a distância da imagem ao espelho P’ é a própria distância focal f do espelho  P’ = f = 0,2 m.

 =    =   i = –   i = – 0,04m  i = – 4 cm (a imagem tem altura de 4 cm e é invertida em relação ao objeto)

14- Veja abaixo a representação do raio de luz no plano cartesiano:

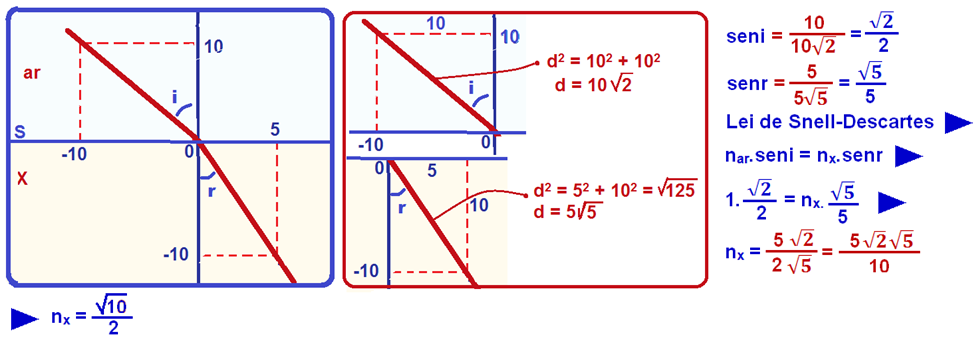
R- E

15- Vamos pensar em todas as alternativas:

No caso de A há uma refração, pois a luz passou de um ambiente para outro, o que não muda é o ângulo de refração.

Em B o ângulo é de 0°, pois está localizado em cima do eixo normal.

Na alternativa C, a frequência não muda quando se troca de ambiente, a velocidade se altera. Sendo assim, a alternativa D é a correta, pois quando se modifica a velocidade de propagação o comprimento de onda também se altera, basta analisar a fórmula abaixo:

Onde:

V é a velocidade de propagação

 é o comprimento de onda

f é a frequência

16-
Lei de Snell-Descartes (refração da luz)

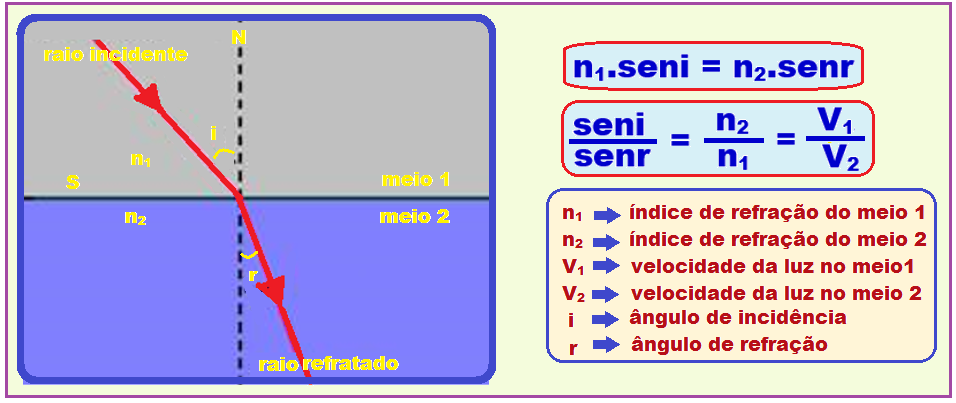
nar.sen45o = nágua.senr  1./2 = 1,5.senr  senr =  =  0,47  pelos valores

fornecidos no enunciado você observa que  <  , ou seja, menor que 30o.

R- A

17-

Vamos usar a imagem a seguir como apoio:

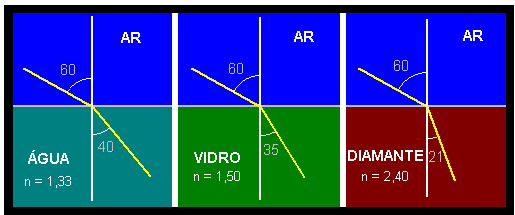
Nela podemos observar que quanto mais refringente (quanto maior o índice de refração), mais o raio refratado se aproxima da reta normal (reta que usamos de referência), no caso do exercício, a linha pontilhada. Ao observarmos o exercício, podemos concluir que o meio A tem que ser o lantânio, pois só assim há uma aproximação em um caso e um distanciamento no outro, já que ele é o valor intermediário. Ainda sobra o problema de B e C, que podemos concluir observando a imagem de apoio, que em B se trata de diamante (há uma aproximação à reta normal) e C se trata de vidro crown (há um afastamento à reta normal).

R – E

18-

a) O índice de refração absoluto aplicado ao material do cilindro constituído de um meio homogêneo e transparente é fornecido por:

n = 1,6 e c = 3.108 m/s  n =   1,6 =   V =   V = 1,875 m/s

b)

Aplicando a lei de Snell-Descartes na refração do feixe de luz em A, do ar para o cilindro  nar.seni = n.senr  1.sen53^o = 1,6.senr  1.0,8 = 1,6.senr  senr =  = 0,5  r = 30^o.

Observe atentamente a figura abaixo:

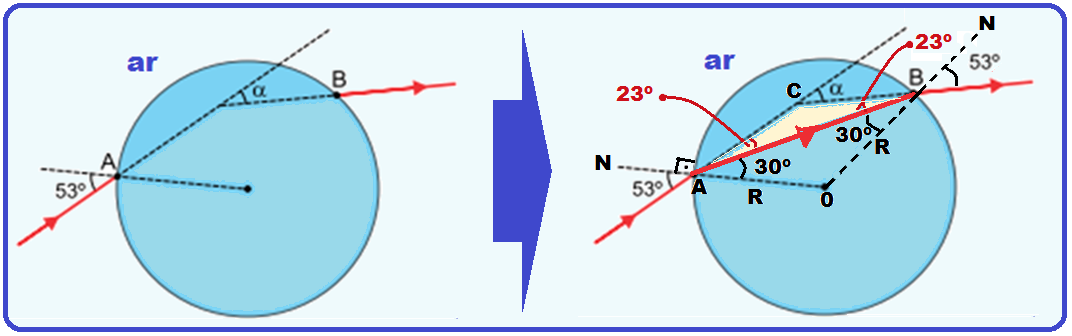
Se o ângulo de incidência (com a normal N) em A é de 53^o, o ângulo de emergência em B (com a normal N) também será de 53^o, pois os meios são os mesmos.

Como o triângulo AOB é isósceles (dois lados iguais R) então seus ângulos opostos são iguais (30^o).

No triângulo ABC o ângulo α é externo o que implica que α = 2×23 = 46^o

19- Breve teoria

Na figura 1 o ponto objeto real P está dentro da água (mais refringente, maior índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao se refratar para o ar, afasta-se da normal atingindo os olhos do observador e determina a imagem virtual (P’), obtida no prolongamento desse raio e onde ele intercepta o raio de luz vertical, fornecendo essa imagem P’, acima do objeto real P.

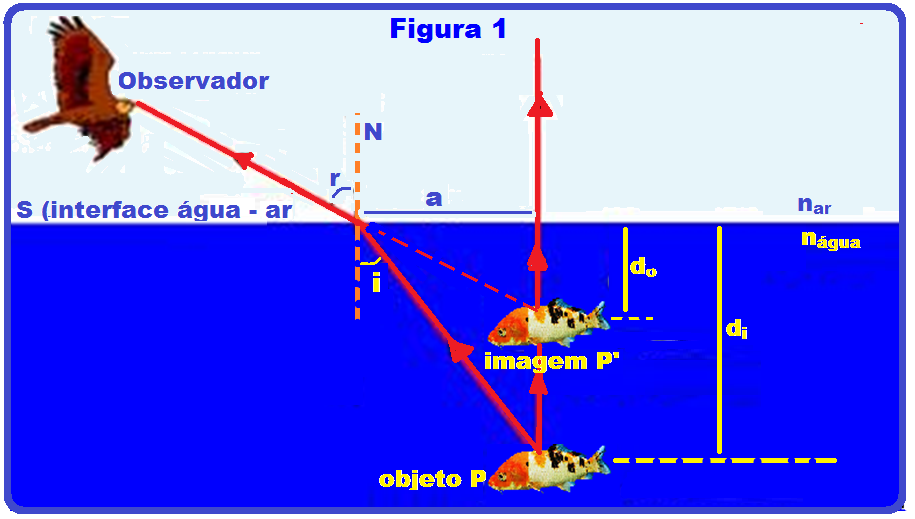
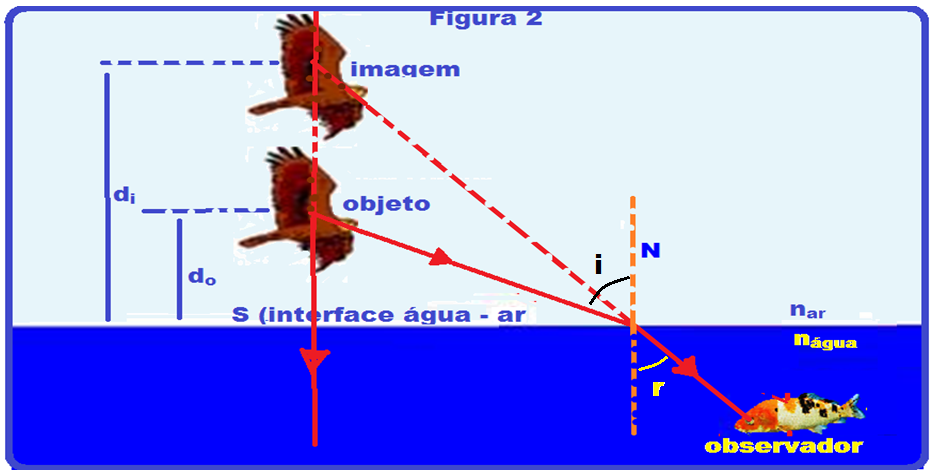
 Na figura II o ponto objeto real P está no ar (menos refringente, menor índice de refração) e emitindo dois raios de luz, um vertical que não sofre desvio e o outro oblíquo que, ao refratar-se para  a água aproxima-se da normal atingindo os olhos do observador e determina a imagem virtual P’, acima do objeto real P.

Observe que, em ambos os casos a imagem está sempre acima do objeto.

R- B

20- Veja na figura da esquerda os ângulos que confirmam que o ângulo de incidência do raio de luz na interface ar – líquido (ponto A) vale i = 60^o.

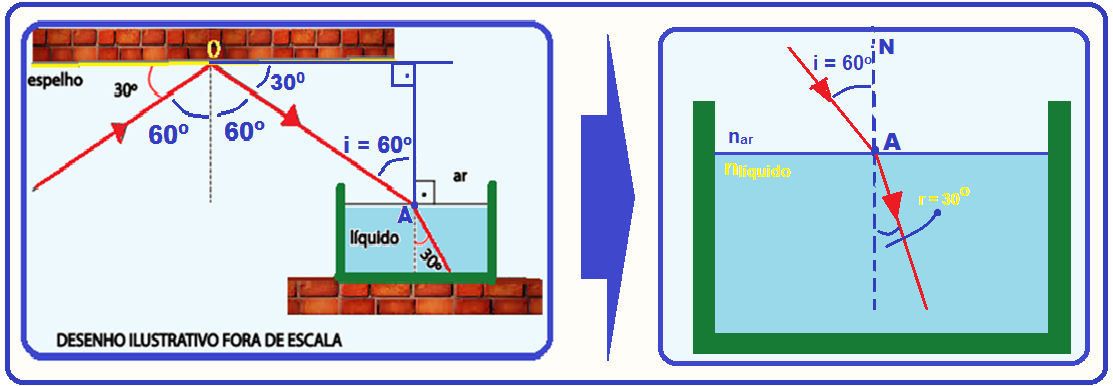
Aplicando a lei de Snell – Descartes na figura da direita acima no ponto Ada interface ar – líquido

Nar.seni = nlíquido.senr  1.sen60^o = nlíquido.sen30^o  1. = nlíquido.  nlíquido =

R- C

21- Podemos resolver esta questão através da Lei de Snell-Descartes  

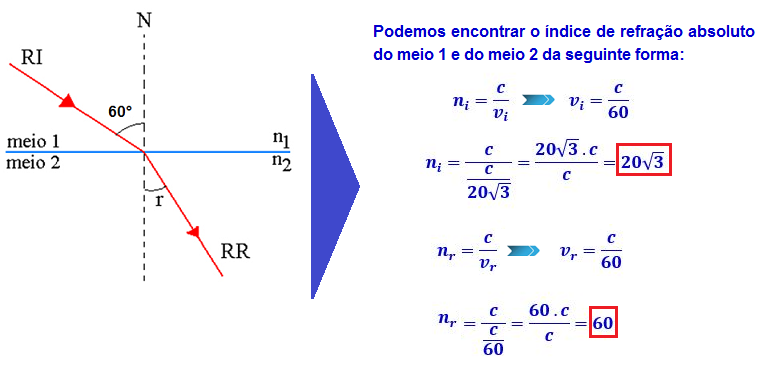
Temos, então, que          

R- Portanto, a resposta correta é a alternativa A.

22-

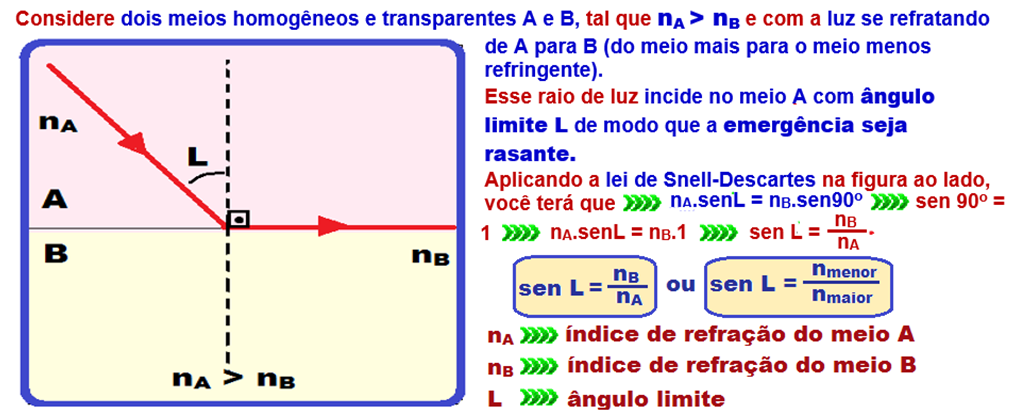
Os pontos do tubo retilíneo luminescente que podem ser vistos por pessoas fora da piscina são aqueles localizados abaixo do ponto M já que os pontos acima de M serão impedidos de se refratarem pela boia circular opaca.

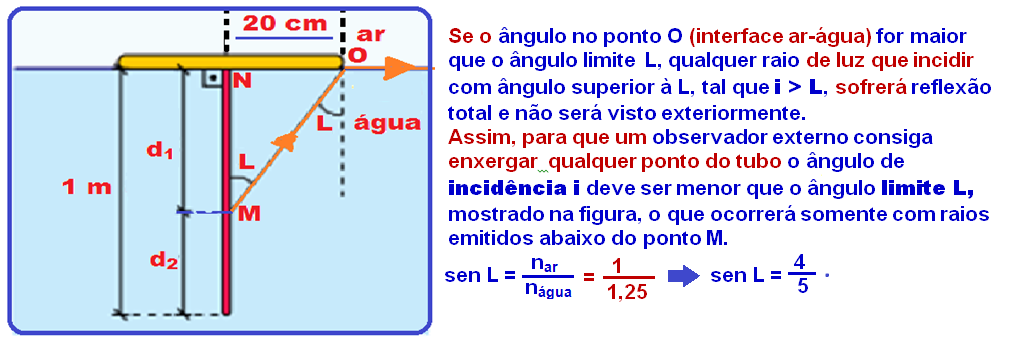
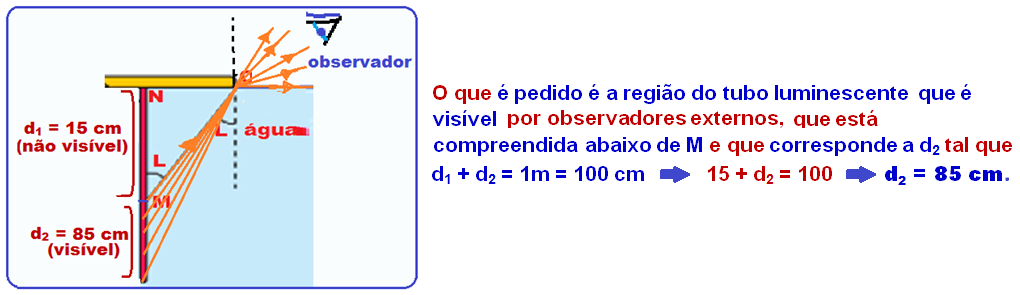
R – B

23-

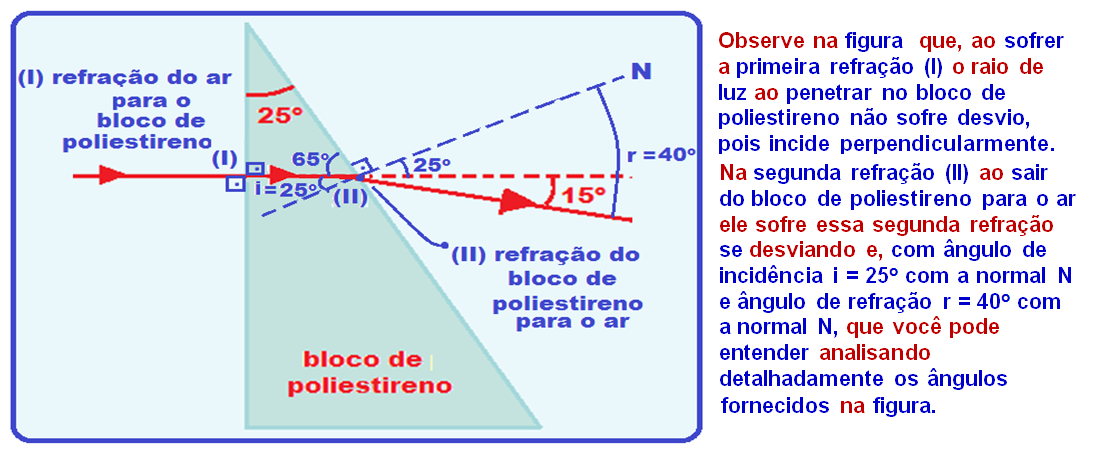
Aplicando em (II) a lei de Snell-Descartes  npoliestireno.seni = nar .senr  npoliestireno.sen25^o = 1.sen40^o  npoliestireno.0,4 = 1.0,6  npoliestireno=   npoliestireno = 1,5.

R- B

24-
Índice de refração

Observe na expressão acima que, sendo a velocidade c da luz constante, a velocidade v de propagação da luz no meio (no caso, o vidro) é inversamente proporcional ao índice absoluto de refração da luz nesse meio.

A dispersão luminosa ocorre artificialmente quando a luz se dispersa como no interior de um prisma (ou no interior da esfera de vidro do exercício) ou quando passa do ar para a água, sendo mais desviada a luz monocromática violeta (menor velocidade) e menos desviada a luz monocromática vermelha (maior velocidade).

Como, pelo enunciado, o índice refração absoluto do vidro é maior para a cor azul do que para a

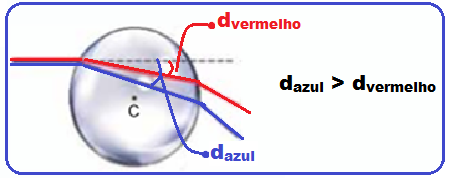
vermelha, a luz azul, no interior do vidro sofre maior desvio ao atravessar a esfera (veja figura acima).

R- B

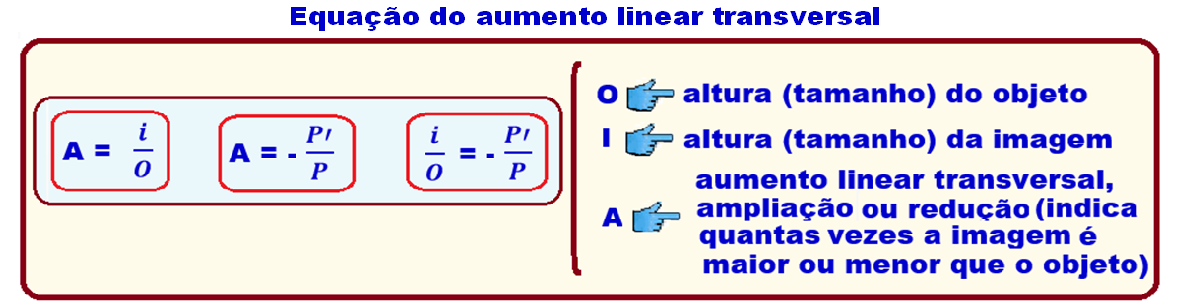
25- A) Veja a equação de Gauss abaixo:

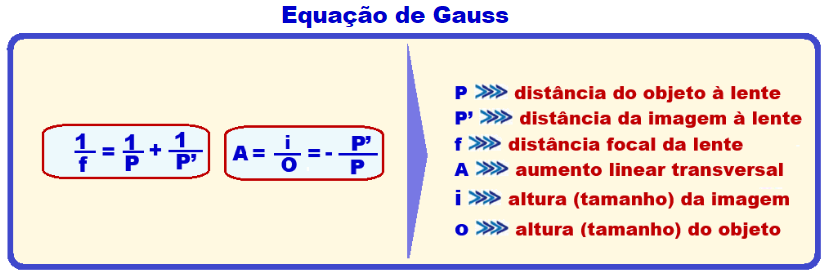
Sendo a lente a mesma, a distância focal f também é a mesma e aampliação A (aumento linear transversal) é fornecida pela expressão A = – que mostra que A depende apenas das distâncias do objeto e da imagem à lente.

Se a ampliação fosse a mesma nas duas posições, P1 seria igual à P1’, P2seria igual à P2’ e │A│= │1│(objeto e imagem teriam o mesmo tamanho).

Observe na figura que, com o objeto mais próximo da lente P1’ > P1 e│A1│> │1│(tamanho aumentado).

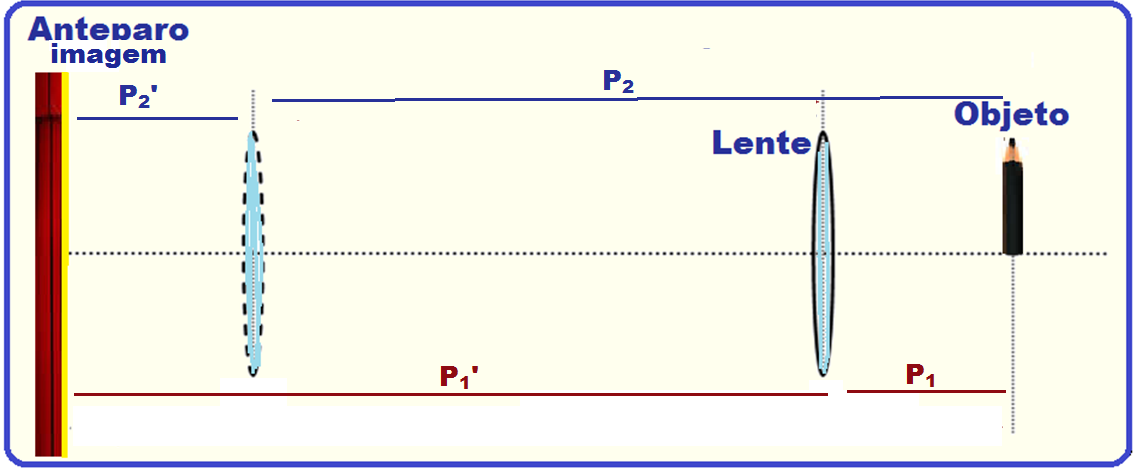
Da mesma maneira, com o objeto mais afastado da lente P2’ < P2 e │A2│< │1│(tamanho diminuído).

B) Está sendo pedida a distância entre o objeto e a lente na situação em que estão mais próximos entre si (posição P), ou seja, está pedindo P1.

Nessas condições a distância do objeto à lente será P1 e da imagem à lente P1’ = L – P1 = 10 – P1 e

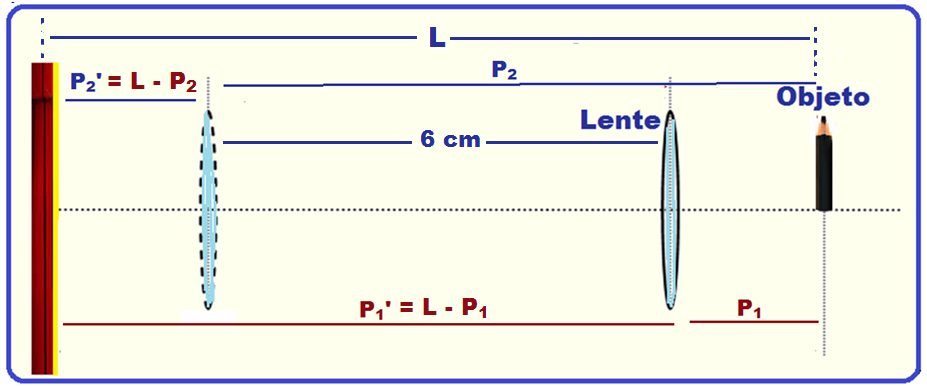
na outra posição a distância do objeto à lente será P2 e da imagem à lente P2’ = L – P2 = 10 – P2.

Observe ainda, na figura acima, que P2 – P1 = 6 (I).

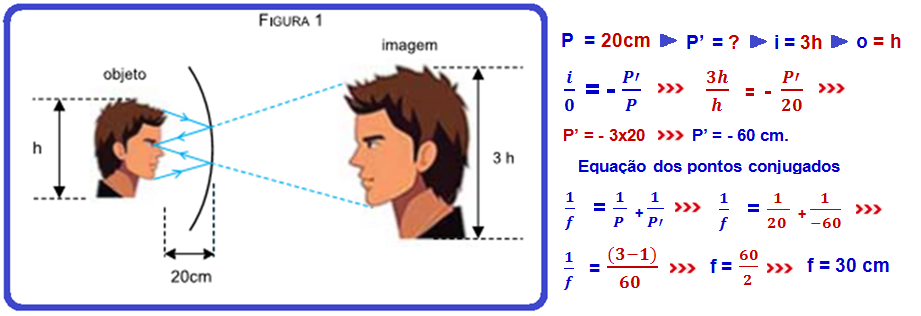
26- Primeiramente precisamos encontrar o valor da distância da imagem ao espelho, para isso vamos utilizar a equação do aumento linear:

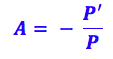
Onde:

A é o aumento linear

P’ é a distância da imagem ao espelho

P é a distância do objeto ao espelho

Isolando P’:

Substituindo, sabendo que o A foi dado no texto, quando ele diz que o aumento é de 5 vezes. Deixaremos tudo em cm, pois a resposta final está em cm:

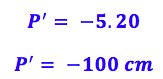
Agora que já temos a distância da imagem, podemos substituir na fórmula de gauss:

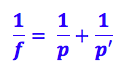
Onde:

f é a distância focal

p é a distância do objeto ao espelho

p’ é a distância da imagem ao espelho

Substituindo os valores, já jogando o sinal negativo (-100 cm) para fora da fração, ficando sinal negativo:

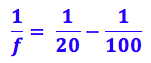
Resolvendo:

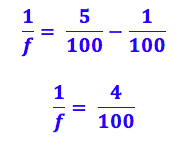
Multiplicando tudo por -1, ou seja, invertendo as frações:

R – B

27- A lupa é uma lente convergente e todos os raios de luz que incidem paralelamente ao eixo principal (caso do sol a pino) emergem da lente convergindo para o foco f. Assim, no caso do exercício, f = h.

Veja a construção geométrica da imagem em uma lupa (lente convergente) em que o objeto tem que estar entre f_o = f = h e O.

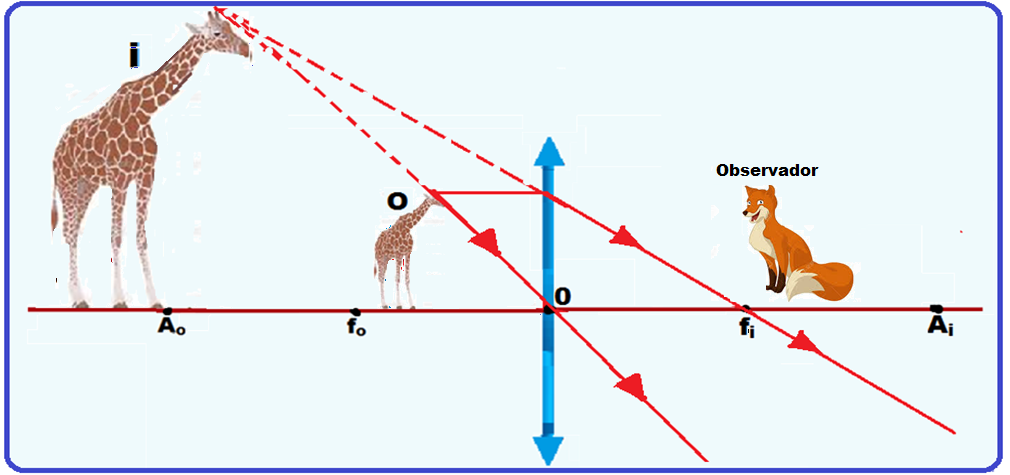
Natureza  Virtual (obtida no cruzamento dos prolongamentos dos raios luminosos).

Localização  Antes de fo

Tamanho e orientação  maior que o objeto e direita em relação a ele.

R- D

28- Uma das imagens i do objeto que está antes do ponto antiprincipal Ao (200 cm) é formada diretamente pela lente biconvexa (convergente) que tem as seguintes características, geometricamente localizadas na figura abaixo:

Objeto O antes de Ao

Características da imagem i:

Natureza  Real (obtida no cruzamento do próprio raio luminoso (linha cheia)).

Localização  entre Fi e Ai.  

Tamanho e orientação  menor que o objeto e invertida em relação ao mesmo.

A outra imagem i’ captada pelo espelho plano (real, invertida e maior que o objeto, pois o

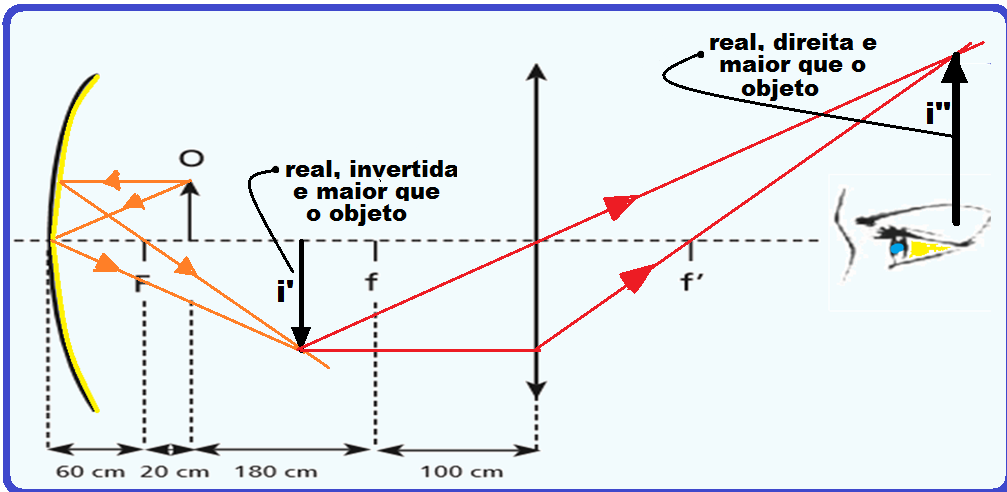
objeto está a 80cm do espelho, entre o foco F = 60cm e o centro de curvatura C = 120 cm) funciona como objeto para a lente biconvexa (convergente) e sua imagem i’’, vista pelo observador será direita em relação ao objeto, real e maior que o mesmo, conforme construção geométrica na figura acima.

R- B

29-

Nesse microscópio de luz, a velocidade de propagação da luz é constante e vale V = c = 3.10⁸ m/s, e assim, pela equação fundamental da ondulatória V = constante =c = λ.f, o comprimento de onda λ é inversamente proporciona à frequência f.

Como pelo enunciado, o intervalo de frequências do espectro de luz visível está compreendido entre 4,0.10¹⁴ Hz e 7,5.10¹⁴ Hz, a menor estrutura celular (menor λ) que se poderia observar nesse microscópio de luz corresponde à maior frequência nesse intervalo que é de é de f = 7,5.10¹⁴ Hz.

c = λ.f  3.10⁸ = λ.7,5.10¹⁴  λ =   λ = 0,4.10^-6  λ = 4.10^-7 m = 400 nm.

Portanto, observando a figura você percebe que a menor estrutura celular que você pode perceber nesse microscópio é o Retículo Endoplasmático dimensão 420 nm.

R- B

30-

Questões de Vestibulares recentes por assunto

2014 – 2013 - Óptica

01-(FUVEST-SP-014)

A primeira medida da velocidade da luz, sem o uso de métodos astronômicos, foi realizada por Hippolyte Fizeau, em 1849.  A figura mostra um esquema simplificado da montagem experimental por ele utilizada. 

Um feixe fino de luz, emitido pela fonte F, incide no espelho plano semitransparente E1.

A luz refletida por E1 passa entre dois dentes da roda dentada R, incide perpendicularmente no espelho plano E2 que está a uma distância L da roda, é refletida e chega ao olho do observador. 

A roda é então colocada a girar em uma velocidade angular tal que a luz que atravessa o espaço entre dois dentes da roda e é refletida pelo espelho E2, não alcance o olho do observador, por atingir o dente seguinte da roda. Nesta condição, a roda, com N dentes, gira com velocidade angular constante e dá V voltas por segundo.

a) Escreva a expressão literal para o intervalo de tempo Δt em que a luz se desloca da roda até E2 e retorna à roda, em função de L e da velocidade da luz c.

b)Considerando o movimento de rotação da roda, escreva, em função de N e V, a expressão literal 

para o intervalo de tempo Δt decorrido entre o instante em que a luz passa pelo ponto central entre 

os dentes A e B da roda e o instante em que, depois de refletida por E2, é bloqueada no centro do dente B.  

c) Determine o valor numérico da velocidade da luz c, utilizando os dados abaixo.

02-(FUVEST-SP-014)

Um estudanteconstruiu um microscópio ótico digital usando  uma webcam,  da qual ele removeu a 

lente original. Ele preparou um tubo adaptador e fixou uma lente convergente, de distância focal f = 50 mm, a umadistância d = 175 mm do sensor de imagem da webcam, como visto na figura abaixo.  

No manual da webcam, ele descobriu que seu sensor de imagem tem dimensão total útil de 6x6 

mm2, com 500x500 pixels. Com estas informações, determine 

a) as dimensões do espaço ocupado por cada pixel; 

 b) a distância L entre a lente e um objeto, para que este fique focalizado no sensor; 

 c)o diâmetro máximo D que uma pequena esfera pode ter, para que esteja integralmente dentro do campo visual do microscópio, quando focalizada. 

03-(FUVEST-SP-014)

Um prisma triangular desvia um feixe de luz verde de um ângulo Ө_A, em relação à direção de incidência, como ilustra a figura A. Se uma placa plana, do mesmo material do prisma, for colocada entre a fonte de luz e o prisma, nas posições mostradas nas figuras B e C, a luz, ao sair do prisma, será desviada,

respectivamente, de ângulos ӨB e ӨC, em relação à direção de incidência indicada pela seta.Os desvios angulares serão tais que

04-(UNESP-SP-014)

Uma pessoa está parada numa calçada plana e horizontal diante de um espelho plano vertical E pendurado na fachada de uma loja. A figura representa a visão de cima da região.

Olhando para o espelho, a pessoa pode ver a imagem de um motociclista e de sua motocicleta que passam pela rua com velocidade constante V = 0,8 m/s, em uma trajetória retilínea paralela à calçada, conforme indica a linha tracejada. Considerando que o ponto O na figura represente a posição dos olhos da pessoa parada na calçada, é correto afirmar que ela poderá ver a imagem por inteiro do motociclista e de sua motocicleta refletida no espelho durante um intervalo de tempo, em segundos, igual a

05-(UNESP-SP-014)

Para observar uma pequena folha em detalhes, um estudante utiliza uma lente esférica convergente funcionando como lupa. Mantendo a lente na posição vertical e parada a 3 cm da folha, ele vê uma imagem virtual ampliada 2,5 vezes.

Considerando válidas as condições de nitidez de Gauss, a distância focal, em cm, da lente utilizada pelo estudante é igual a

(A) 5. (B) 2. (C) 6. (D) 4. (E) 3.

06-(UNICAMP-SP-014)

O sistema de imagens street view disponível na internet permite a visualização de vários lugares do

mundo através de fotografias de alta definição, tomadas em 360 graus, no nível da rua.

Em uma câmera fotográfica tradicional, a imagem é gravada em um filme fotográfico para posterior

revelação. A posição da lente é ajustada de modo a produzir a imagem no filme colocado na parte posterior da câmera.

Considere uma câmera para a qual um objeto muito distante fornece uma imagem pontual no filme em uma posição P’=5cm.O objeto é então colocado mais perto da câmera, em uma posição P=100cm, e a distância entre a lente e o filme é ajustada até que uma imagem nítida real invertida se forme no filme, conforme mostra a figura.

Obtenha a variação da posição da imagem p’ decorrente da troca de posição do objeto.

07-(UNIFESP-SP-014)

Dentro de uma casa uma pessoa observa, por meio de um espelho plano E, uma placa com a inscrição VENDO colocada fora da casa, ao lado de uma janela aberta. A janela e o espelho têm as dimensões horizontais mínimas para que o observador consiga ver a placa em toda sua extensão lateral. A figura 1 representa o espelho e a janela vistos de dentro da casa. A figura 2 representa uma visão de cima da placa, do espelho plano E, do observador O e de dois raios de luz emitidos pela placa que atingem, depois de refletidos em E, os olhos do observador.

Considerando as medidas indicadas na figura 2, calcule, em metros:

a) a largura (L) da janela.

b) a largura mínima (x) do espelho E para que o observador possa ver por inteiro a imagem da placa conjugada por ele.

08-(AFA-014)

Um pequeno objeto plano e luminoso pode ser utilizado em três arranjos ópticos distintos (I, II e III), imersos em ar, como apresentado na figura abaixo.

No arranjo I, o objeto é colocado sobre um plano onde se apoiam dois espelhos planos ortogonais entre si. Nos arranjos II e III, respectivamente, o objeto é disposto de forma perpendicular ao eixo óptico de um espelho esférico côncavo gaussiano e de uma lente convergente delgada.

Dessa maneira, o plano do objeto se encontra paralelo aos planos focais desses dois dispositivos. Considere que as distâncias do objeto ao vértice do espelho esférico e ao centro óptico da lente sejam maiores do que as distâncias focais do espelho côncavo e da lente.

Nessas condições, das imagens abaixo, a que não pode ser conjugada por nenhum dos três arranjos ópticos é

09-(AFA-014)

Um estudante montou um experimento com uma rede de difração de 1000 linhas por milímetro, um laser que emite um feixe cilíndrico de luz monocromática de comprimento de onda igual a 4.10-7m e um anteparo, conforme figura abaixo.

O espectro de difração, observado no anteparo pelo estudante, foi registrado por uma câmera digital e os picos de intensidade apareceram como pequenos pontos brilhantes na imagem.

Nessas condições, a opção que melhor representa a imagem do espectro de difração obtida pelo estudante é:

10-(CEFET-MG-014)

No vácuo, um determinado meio material isotrópico e transparente com índice de refração absoluto igual a 2 apresentará a condição de reflexão total para um raio de luz com ângulo limite de incidência igual a _______, propagando-se do ______________________ para o

______________________ .

Os termos que preenchem, corretamente, as lacunas são

a) 30º, material, vácuo. b) 30º, vácuo, material. c) 60º, material, vácuo.

d) 60º, vácuo, material. e) 90º, vácuo, material.

11-(UFSCAR-SP-014)

Para melhorar a qualidade do ar, a administração da cidade de São Paulo exige que seus veículos passem periodicamente por uma inspeção em que são medidos os níveis de emissão de gases poluentes e observadas eventuais irregularidades, como a ausência do filtro catalisador. Para facilitar o trabalho do fiscal, um espelho plano foi estrategicamente montado sobre rodinhas permitindo que, pela reflexão, observe-se a parte debaixo do carro.

Considerando a posição X do olho do fiscal e a posição do espelho plano, é correto afirmar que, dos pontos indicados, o fiscal é capaz de enxergar, no máximo, até o ponto

(A) P. (B) Q. (C) R. (D) S. (E) T.

12-(EsPCEx-SP-014)

Uma fonte luminosa está fixada no fundo de uma piscina de profundidade igual a 1,33 m.

Uma pessoa na borda da piscina observa um feixe luminoso monocromático, emitido pela fonte, que

forma um pequeno ângulo α com a normal da superfície da água, e que, depois de refratado, forma um pequeno ângulo β com a normal da superfície da água, conforme o desenho.

A profundidade aparente "h" da fonte luminosa vista pela pessoa é de:

Dados: sendo os ângulos α e β pequenos, considere tg α ≅ sen α e tg β ≅ sen β

Índice de refração da água: nágua= 1,33

Índice de refração do ar: nar= 1

a) 0,80 m b) 1,00 m c) 1,10 m d) 1,20 m e) 1,33 m

13-(FATEC-SP-014)

Como foi que um arranha-céus “derreteu” um carro?

“É uma questão de reflexo. Se um prédio é curvilíneo e tem várias janelas planas, que funcionam com

o espelhos, os reflexos se convergem em um ponto” diz Chris Shepherd, do Instituto de Física de

Londres.

O edifício de 37 andares, ainda em construção, é de fato um prédio curvilíneo e o carro, um Jaguar,

estava

estacionado em uma rua próxima ao prédio, exatamente no ponto atingido por luzes refletidas e não

foi o único que sofreu estrago.

O fenômeno é consequência da posição do Sol em um determinado período do ano e permanece

nessa posição por duas horas por dia. Assim, seus raios incidem de maneira oblíqua às janelas do edifício.

Considerando o fato descrito e a figura da pessoa observando o reflexo do Sol no edifício, na mesma posição em que estava o carro quando do incidente, podemos afirmar corretamente que o prédio se assemelha a um espelho

(A) plano e o carro posicionou-se em seu foco infinito.

(B) convexo e o carro posicionou-se em seu foco principal.

(C) convexo e o carro posicionou-se em um foco secundário.

(D) côncavo e o carro posicionou-se em seu foco principal.

(E) côncavo e o carro posicionou-se em um foco secundário

14-(FGV-SP-014)

A lupa é um instrumento óptico constituído por uma lente de aumento. Para cumprir sua função, ela

deve ser

(A) divergente e estar posicionada a uma distância do objeto analisado menor que sua distância focal.

(B) divergente e estar posicionada a uma distância do objeto analisado compreendida entre o foco e

o ponto antiprincipal

da lente.

(C) convergente e estar posicionada a uma distância do objeto analisado menor que sua distância

focal.

(D) convergente e estar posicionada a uma distância do objeto analisado compreendida entre o foco e o ponto antiprincipal.

(E) convergente e estar posicionada a uma distância do objeto analisado maior que a distância focal.

15-(MACKENZIE-SP-014)

Dispõe-se de um espelho convexo de Gauss, de raio de curvatura R. Um pequeno objeto colocado

diante

desse espelho, sobre seu eixo principal, a uma distância R de seu vértice V, terá uma imagem conjugada situada no ponto P desse eixo. O comprimento do segmento VP é

a) R/4 b) R/3 c) R/2 d) R e) 2 R

16-(PUC-SP-014)

Um estudante de física resolve brincar com espelhos esféricos e faz uma montagem, utilizando um

espelho

esférico côncavo de raio de curvatura igual a 80 cm e outro espelho convexo de raio de curvatura cujo

módulo é igual a 40 cm. Os espelhos são cuidadosamente alinhados de tal forma que foram montados coaxialmente, com suas superfícies refletoras se defrontando e com o vértice do espelho convexo coincidindo com

a posição do foco principal do espelho côncavo. O aluno, então, colocou cuidadosamente

um pequeno objeto no ponto médio do segmento que une os vértices desses dois espelhos. Determine, em relação ao vértice do espelho convexo, a distância, em centímetros, da imagem, formada por esse espelho ao receber os raios luminosos que partiram do objeto e foram refletidos pelo espelho côncavo, e classifique-a.

(A) 16cm, virtual e direita (B) 16cm, virtual e invertida (C) 40cm, real e direita

(D) 40cm, virtual e direita (E) 13,3cm, virtual e invertida

Princípios da propagação da luz

55-(PUC-RJ-013)

A uma certa hora da manhã, a inclinação dos raios solares é tal que um muro de 4,0 m de altura projeta, no chão horizontal, uma sombra de comprimento 6,0 m.

Uma senhora de 1,6 m de altura, caminhando na direção do muro, é totalmente coberta pela sombra quando se encontra a quantos metros do muro?

(A) 2,0                (B) 2,4                     (C) 1,5                     (D) 3,6                        (E) 1,1

56-(UFT-TO-013)

Um arco-íris se forma quando o Sol, as gotas de chuva e o observador estão dispostos em um

determinado ângulo.

Os raios de sol penetram na gota de chuva e, devido à forma da gota, emergem com a luz separada

nos seus vários comprimentos de onda, atingindo então o olho do observador.

O fenômeno que ocorre com a luz na formação do arco-íris é chamado de:

(A) Difração, interferência, dispersão.                                 (B) Interferência, reflexão, polarização.

(C) Polarização, interferência, difração.                               (D) Reflexão, polarização, dispersão.

(E) Refração, reflexão, dispersão.

Reflexão da luz e espelhos planos

51-(URCA-CE-013)

Um raio de luz incide no ponto O, meio A, da superfície de separação entre esse meio e o meio B, com um ângulo de incidência igual a 7o. No interior do meio B, o raio incide em um espelho côncavo E, passando pelo foco principal F. O centro de curvatura C do espelho, cuja distancia focal é igual a 1,0m, encontra-se a 1,0m da superfície de separação dos meios A e B. Observe a figura abaixo:

Considere os seguintes índices de refração: nA = 1,0 (meio A); nB = 1,2 (meio B).

Determine a que distancia do ponto O, o raio emerge, após a reflexão no espelho. Dado sen7o = 0,12

a) 10 cm                   b) 15 cm                       c) 20 cm                      d) 25 cm                             e) 30 cm

Associação de espelhos planos

29-(UNICAMP-SP-013)

Em um aparelho experimental, um feixe laser emitido no ponto P reflete internamente três vezes e

chega ao ponto Q, percorrendo o trajeto PFGHQ. Na figura abaixo, considere que o comprimento do

segmento PB é de 6 cm, o do lado AB é de 3 cm, o polígono ABPQ é um retângulo e os ângulos de

incidência e reflexão são congruentes, como se indica em cada ponto da reflexão interna. Qual é a

distância total percorrida pelo feixe luminoso no trajeto PFGHQ?

a) 12 cm.                  b) 15 cm.                        c) 16 cm.                        d) 1 8

30-(FUVEST-SP-013)

O telêmetro de superposição é um instrumento ótico, de concepção simples, que no passado foi

muito utilizado em

 câmeras fotográficas e em aparelhos de medição de distâncias. Uma representação esquemática de

um desses instrumentos está na página de respostas. O espelho semitransparente E1 está

posicionado a 45o em relação à linha de visão, horizontal, AB. O espelho E2 pode ser girado, com

precisão, em torno de um eixo perpendicular à figura, passando por C, variando-se assim o ângulo

β entre o plano de E2 e a linha horizontal. Deseja-se determinar a distância AB do objeto que está no

ponto B ao instrumento.

a) Desenhe na figura da página de respostas, com linhas cheias, os raios de luz que, partindo do

objeto que está em B, atingem o olho do observador - um atravessa o espelho E1 e o outro é refletido

por E2 no ponto C. Suponha que ambos cheguem ao olho do observador paralelos e superpostos.

b) Desenhe, com linhas tracejadas, o trajeto aproximado de um raio de luz que parte do objeto em B',

incide em C e é refletido por E2.

Com o objeto em um ponto B específico, o ângulo β foi ajustado em 44º, para que os raios cheguem ao olho do observador paralelos e superpostos. Nessa condição,

c) determine o valor do ângulo γ entre as linhas AB e BC;

d) com AC = 10 cm, determine o valor de AB.

Espelhos esféricos-construção de imagens

34-(UFV-MG-013)

Utilizando-se um espelho esférico, deseja-se obter uma imagem virtual, direta e maior do que um

objeto. Para que isso

ocorra é CORRETO afirmar que o objeto deve estar localizado na frente de um espelho:

a) côncavo a uma distância maior que a distância focal deste.

b) côncavo a uma distância menor que a distância focal deste.

c) convexo a uma distância menor que a distância focal deste.

d) convexo a uma distância maior que a distância focal deste.

35-(PUC-RS-013)

Ao observar a imagem da Lua formada por um pequeno espelho côncavo, um astrônomo amador na

Terra percebe que esta imagem se forma

A) aproximadamente no foco do espelho.            B) aproximadamente no centro do espelho.

C) a meia distância entre o foco e o vértice do espelho.            D) a meia distância entre o centro e o

foco do espelho.

E) exatamente no vértice do espelho.

Estudo analítico dos espelhos esféricos

27-(UNIMONTES-MG-013)

Um espelho de barbear côncavo, com raio de curvatura de 30cm, é posicionado de tal forma que

amplia três

vezes o rosto de um homem em uma imagem não invertida. A que distância do rosto do homem

está o espelho?

A) 10cm.                       B) 20cm.                                C) 30cm.                         D) 40cm.

28- (PUC-SP-013)

Um objeto é inicialmente posicionado entre o foco e o vértice de um espelho esférico côncavo, de raio de curvatura

igual a 30cm, e distante 10cm antes do foco. Quando o objeto for reposicionado para a posição

correspondente ao

centro de curvatura do espelho, qual será a distância entre as posições das imagens formadas

nessas duas situações?

a) 37,5cm                         b) 22,5cm                          c) 7,5cm                       d) 60cm                               e) Zero

Refração luminosa-conceitos e definições

27-(FGV-RJ-013)

Em uma piscina, uma pessoa de visão normal, sem óculos e com olhos abertos dentro da água,

enxerga desfocada uma planta que está fora da água. Ao sair da piscina, enxerga nitidamente a

mesma planta. A partir dessa observação, e sabendo que a córnea é responsável por grande parte da

capacidade de focalização do olho humano, é correta a conclusão de que os índices de refração do ar,

da água e da córnea, respectivamente nar, nag e nc, obedecem à relação:

A. nar < nc < nag         B. nar > nc > nag             C. nar ≈ nc < nag        -D. nar < nc ≈ nag            E. nar > nc ≈ nag

Leis da refração

30-(PUC-RJ-013)

I – Quanto maior a frequência de uma onda luminosa,  maior a sua velocidade de propagação.

II – Quando um feixe de luz passa de um meio a outro, seu comprimento de onda muda, mas sua

velocidade se mantém constante.

III – O fenômeno de reflexão total pode ocorrer quando um feixe luminoso passa de um meio mais

refringente para outro menos refringente.

São corretas as seguintes afirmações:

(A) I, II e III.          (B) I e III, apenas.        (C) III, apenas.                (D) II e III, apenas.              (E) I, apenas.

Reflexão total

41-(UNCISAl-AL-013)

 A endoscopia permite a visualização de estruturas internas do corpo humano. Um dos aparelhos

utilizados para esse fim é o fribroscópio, que utiliza fibras ópticas. O funcionamento dessas fibras

está baseado no princípio da reflexão interna total da luz, cujas características podem ser

determinadas a partir da Lei de Snell-Descartes. Dadas, então, as afirmativas seguintes,

I. Para que ocorra reflexão interna total em uma interface é necessário que a luz se propague de um

meio de índice de refração menor para um meio de índice de refração maior.

II. O ângulo crítico ou limite (medido em relação à reta normal à interface) para a ocorrência de

reflexão interna total é dado por senL =n2/n1, onde n1 é o índice de refração do meio que o feixe

está propagando-se inicialmente e n2 é o índice de refração do meio que o feixe iria propagar-se

caso não ocorresse reflexão interna total.

III. Para um ângulo de incidência na interface (medido em relação à reta normal à interface) maior que

o ângulo crítico ou limite não há reflexão interna total.

IV. Não é possível determinar o desvio sofrido por um feixe de luz ao cruzar uma interface através da

Lei de Snell-Descartes.

verifica-se que está(ão) correta(s)

A) I, apenas.        B) II e III, apenas.              C) II, apenas.                  D) I, II, III e IV.              E) IV, apenas.

42-(UFPE-PE-013)

A figura mostra um par de fibras ópticas, A e B, dispostas paralelamente e de mesmo comprimento.

Um pulso de luz disparado em uma das extremidades das fibras. A luz se propaga, parte pela fibra A,

levando o tempo ∆tA para percorrer a fibra , e parte pela fibra B , levando o tempo ∆tB para percorrer

a fibra . Os índices de refração dos materiais da fibra A e B são, respectivamente, nA=1,8 e nB=1,5.

Calcule o atraso percentual da luz que vem pela fibra A, em relação à que vem pela fibra B. Ou seja,

determine a quantidade (∆tA/∆tB – 1)x100%.

43-(UNESP-SP-013)

Uma haste luminosa de 2,5 m de comprimento está presa verticalmente a uma boia opaca circular de

2,26 m de raio, que flutua nas águas paradas e transparentes de uma piscina, como mostra a figura.

Devido à presença da boia e ao fenômeno da reflexão total da luz, apenas uma parte da haste pode

ser vista por observadores que estejam fora da água.

Considere que o índice de refração do ar seja 1,0, o da água da piscina 4/3, sen 48,6º = 0,75 e tg 48,6º

= 1,13. Um observador que esteja fora da água poderá ver, no máximo, uma porcentagem do

comprimento da haste igual a

(A) 70%.                 (B) 60%.                      (C) 50%.                       (D) 20%.                      (E) 40%.

Dioptro plano

23-(FGV-RJ-013)

Em uma piscina, uma pessoa de visão normal, sem óculos e com olhos abertos dentro da água,

enxerga desfocada uma planta que está fora da água. Ao sair da piscina, enxerga nitidamente a

mesma planta. A partir dessa observação, e sabendo que a córnea é responsável por grande parte da

capacidade de focalização do olho humano, é correta a conclusão de que os índices de refração do

ar, da água e da córnea, respectivamente nar, nag e nc, obedecem à relação:

A. nar < nc < nag     B. nar > nc > nag     C. nar ≈ nc < nag    D. nar < nc ≈ nag      E. nar > nc ≈ nag

24-(ENEM-MEC-012)

 Alguns povos indígenas ainda preservam suas tradições realizando a pesca com lanças,

demonstrando uma notável habilidade.

Para fisgar um peixe em um lago com águas tranquilas o índio deve mirar abaixo da posição em que

enxerga o peixe, Ele deve proceder dessa forma porque os raios de luz: