
HIDROSTÁTICA – 2017 – 2016 e 2015
Densidade e Pressão
01-(FMJ-SP-017)

A pressão atmosférica ao nível do mar é aproximadamente 1,0 × 105 Pa e se deve ao peso da coluna de ar existente entre a superfície e a camada mais externa da atmosfera.
Suponha que um cilindro aberto nas extremidades, com a base de área igual a 2,0 m² e apoiada na superfície ao nível do mar, tenha a mesma altura que a atmosfera terrestre. Considerando a aceleração gravitacional igual a 10 m/s², e constante em toda extensão vertical do cilindro, a massa de ar contida nesse cilindro é
(A) 8,0 × 103 kg.
(B) 5,0 × 105 kg.
(C) 2,0 × 104 kg.
(D) 5,0 × 103 kg.
(E) 2,0 × 106 kg.
02-(UEM-PR-015)

Considerando os conceitos relativos à pressão, assinale o que for correto.
01) Pressão é uma grandeza vetorial, portanto tem módulo, direção e sentido definidos.
02) A diferença de pressão entre dois pontos no interior de um líquido homogêneo e em equilíbrio é
proporcional à diferença de profundidade entre esses dois pontos.
04) No sistema internacional de medidas (SI) a unidade de pressão é o Pascal (Pa).
08) Quando um dado ponto de um líquido em equilíbrio no interior de um recipiente sofre uma variação de pressão, essa variação de pressão é transmitida a todos os pontos do líquido e das paredes do recipiente.
16) Estando um líquido em um recipiente aberto, a pressão na superfície do líquido é nula.
03-(EBMSP-BA-017)


Teorema de Stevin – pressão hidrostática - vasos comunicantes
04-(UNIFESO-RJ-015)

Uma esfera está em repouso totalmente imersa em um líquido que se encontra em equilíbrio hidrostático, conforme a figura a seguir.

Assinale a opção que melhor representa, por meio de segmentos orientados, as direções, os sentidos e os módulos das forças de pressão exercidas pelo líquido sobre a esfera.

05-(PUC-RJ-015)

Um tubo cilíndrico de vidro de 5,0 m de comprimento tem um de seus extremos aberto e o outro fechado. Estando inicialmente em contato com o ar à pressão atmosférica (1,0 atm), este tubo é introduzido dentro de uma piscina com água, com a parte fechada para cima, até que a água se haja elevado a um quinto da altura do tubo. O tubo é mantido nesta posição.
Veja a figura.

Suponha que este processo ocorre à temperatura constante. Tome o ar como gás ideal.
Considere:
1 atm = 1,0.105 Pa
g = 10 m/s2
ρágua= 1,0.103 kg/m3
a) Qual é a pressão do ar dentro do tubo, em atm?
b) Qual é a altura H do tubo que se encontra submergida?
06-(UERJ-RJ-015)

Observe o aumento da profundidade de prospecção de petróleo em águas brasileiras com o passar dos anos, registrado na figura a seguir.

Considerando os dados acima, calcule, em atm, a diferença entre a pressão correspondente à profundidade de prospecção de petróleo alcançada no ano de1977 e aquela alcançada em 2003.
dágua do mar=103 kg/m3 e g=10m/s2.
07-(URCA-CE-017)

Suponha que a cada 10 metros de profundidade a pressão hidrostática em um profundo lago aumenta de aproximadamente 1 atmosfera.

Sendo 1 atmosfera a pressão sobre a superfície do lago e 5 atmosferas a pressão total no
no fundo do lago então a profundidade do lago é de:
![]()
Experiência de Torricelli
08-(PUC-RJ-015)

Um tubo cilíndrico de vidro de 5,0 m de comprimento tem um de seus extremos aberto e o outro fechado. Estando inicialmente em contato com o ar à pressão atmosférica (1,0 atm), este tubo é introduzido dentro de uma piscina com água, com a parte fechada para cima, até que a água se haja elevado a um quinto da altura do tubo. O tubo é mantido nesta posição.
Veja a figura.

Suponha que este processo ocorre à temperatura constante. Tome o ar como gás ideal.
Considere:
1 atm = 1,0.105 Pa
g = 10 m/s2
ρágua= 1,0.103 kg/m3
a) Qual é a pressão do ar dentro do tubo, em atm?
b) Qual é a altura H do tubo que se encontra submergida?
Princípio de Pascal
09-(AFA-SP-015)

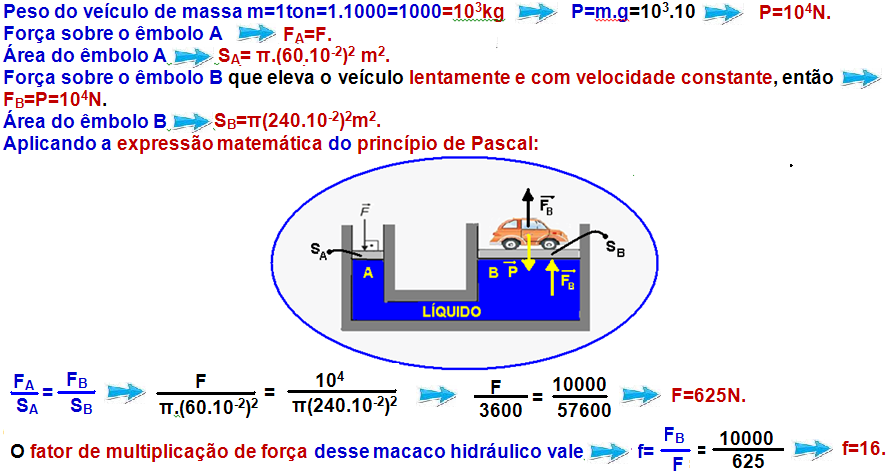
A figura abaixo representa um macaco hidráulico constituído de dois pistões A e B de raios cm RA =

60 cm e RB = 240cm ,respectivamente. Esse dispositivo será utilizado para elevar a uma altura de 2 m, em relação à posição inicial, um veículo de massa igual a 1 tonelada devido à aplicação de
uma
força ![]() .
Despreze as massas
dos pistões, todos
os atritos e
considere que o líquido
seja incompressível.
.
Despreze as massas
dos pistões, todos
os atritos e
considere que o líquido
seja incompressível.
Nessas
condições, o fator
de multiplicação de força deste
macaco hidráulico e o trabalho,
em joules, realizado
pela força ![]() , aplicada
sobre o pistão de menor área,
ao levantar
o veículo bem lentamente e com velocidade constante,
são, respectivamente,
, aplicada
sobre o pistão de menor área,
ao levantar
o veículo bem lentamente e com velocidade constante,
são, respectivamente,
![]()
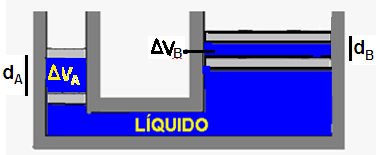
Considerando dA como sendo o deslocamento do êmbolo A e dB como sendo o deslocamento do êmbolo B, possuindo o líquido um volume constante, ou seja, com um líquido incompressível, teremos que o um volume líquido que desce até A, é o mesmo volume líquido que sobe até B.
Teorema de Arquimedes – Empuxo
10-(PUC-MG-015)

Dentro da água, as pessoas sentem uma sensação de estarem mais leves devido à força exercida

pela água sobre o corpo imerso. Esta força descrita por Arquimedes é denominada de empuxo. É CORRETO afirmar:
a) O empuxo é proporcional ao volume de água deslocado pelo corpo.
b) A direção do empuxo pode ser horizontal.
c) O empuxo é sempre menor que o peso do corpo imerso na água.
d) O empuxo é igual ao peso do corpo imerso.
11-(FMJ-SP-015)

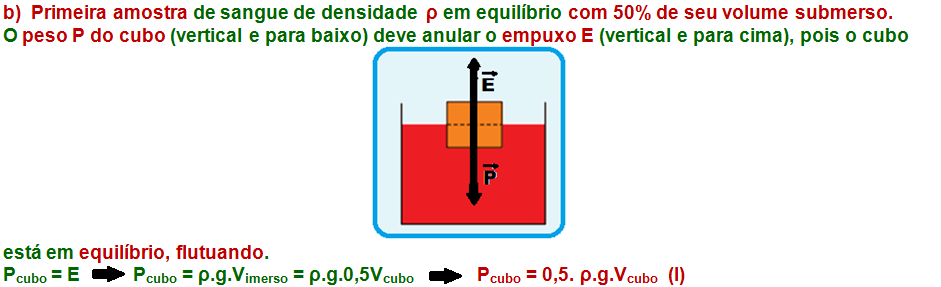
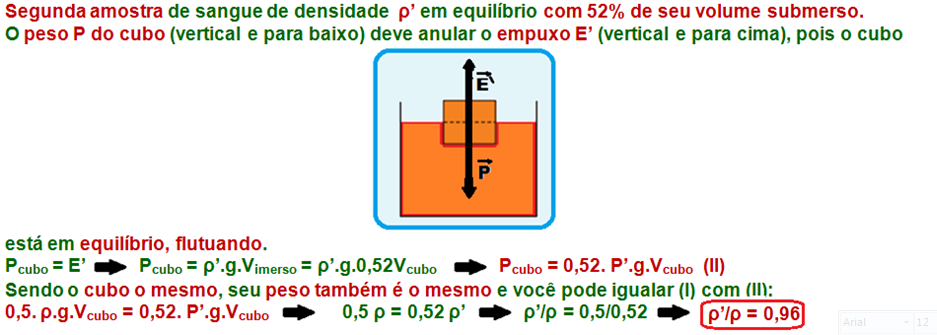
Para determinar a densidade de uma amostra de sangue humano, utiliza-se um cubo de volume V. Colocando-o suavemente sobre a superfície de uma amostra de sangue normal, de densidade absoluta ρ, o cubo flutua com metade de seu volume submerso, como mostra a figura.

Ao colocar-se esse mesmo cubo na superfície de outra amostra de sangue, verifica-se que ele flutua com 52% de seu volume submerso.
a) Deduza uma expressão para a massa do cubo em função de ρ e V.
b) Determine a razão ρ/ρ’, sendo ρ’ a densidade da segunda amostra de sangue.
12-(MACKENZIE-SP-2017)

Um navio flutua por que

a) seu peso é pequeno quando comparado com seu volume.
b) seu volume é igual ao volume do líquido deslocado.
c) o peso do volume do líquido deslocado é igual ao peso do navio.
d) o peso do navio é menor que o peso do líquido deslocado.
e) o peso do navio é maior que o peso do líquido deslocado.
13-(FGV-SP-017)
A figura
a seguir ilustra três cilindros sólidos maciços e homogêneos,
de mesma
área da
base e altura (volumes iguais),em equilíbrio em um líquido.
O cilindro A está completamente submerso, sem tocar no fundo do recipiente, o cilindro B está com metade de seu volume emerso, enquanto o cilindro C apresenta 1/3 de seu volume abaixo da superfície livre do líquido.
Sobre essa situação, é correto afirmar que
(A) a densidade do cilindro A é maior do que a do líquido, pois ele estácompletamente submerso.
(B) a densidade do cilindro B é igual ao dobro da do líquido, pois eledesloca metade do seu volume no líquido.
(C) a densidade do cilindro A é maior do que a do cilindro B, que é maior do que a do cilindro C, em razão dos volumes deslocados no líquido.
(D) pelo fato de estar completamente submerso, o peso do cilindro A é maior do que o empuxo sobre ele e maior que os pesos de B e de C.
(E) o peso do cilindro C é menor do que o empuxo sobre ele porque apenas 1/3 de seu volume está submerso.
14-(Medicina – USCS-SP-017)


15-(CEDERJ-RJ-2017)

Uma
esfera de madeira flutua
imersa, parcialmente, na
água de umaquário
de água doce (sem sal).
Quando essa
água é trocada
por água do mar,
uma nova situação de
equilíbrio é estabelecida. Nessa nova situação, em comparação
à anterior, o empuxo sobre a esfera e o seu volume
submerso são,:
Respectivamente:
(A) o mesmo e maior.
(B) maior e o mesmo.
(C) maior e menor.
(D) o mesmo e menor.
16-(UFPR-PR-017)

Um objeto sólido com massa 600 g e volume 1 litro está parcialmente imerso em um líquido, de

maneira que 80% do seu volume estão submersos.
Considerando a aceleração da gravidade igual a 10 m/s2 , assinale a alternativa que apresenta a massa específica do líquido.
17-(EBMSP-BA-017)

A prática de atividade física na água aquecida traz muitos efeitos terapêuticos benéficos, como o relaxamento, a analgesia, a redução do impacto nas articulações.
Desprezando os efeitos da variação da temperatura e da variação do volume corporal durante a inspiração e a expiração e sabendo que
• o módulo da aceleração da gravidade local é igual a 10m/s2,
• a densidade da água é igual a 1,00g/cm3,
• a densidade do corpo humano é igual a 0,93g/cm3.
Determine o módulo do peso de um objeto que deverá ficar emerso sobre uma pessoa, com

massa igual a 70,0kg, para mantê-la completamente submersa e em equilíbrio, flutuando horizontalmente sob a superfície da água de uma piscina térmica.
18-(PUC-SP-016)
Uma embarcação quando está lastreada, apresenta massa de 10.000kg.
Ela
possui um formato
quadrado cujos lados são iguais a 10m e
é utilizada no
transporte de 2
veículos
pesados por vez,
de uma margem
à outra de um lago de águas tranquilas.
Numa determinada travessia, em que ela transportava dois caminhões idênticos e carregados com igual quantidade de uma mesma carga, verificou-se que a parte submersa dessa embarcação era de 40cm.
Se cada caminhão vazio tem massa de 10 toneladas, determine a massa da carga, em kg, transportada por cada um deles. Dados: Densidade da água= 1g/cm3; Módulo da aceleração da gravidade= 10m/s2
![]()
19-(Mackenzie-SP-016)

Devido à crise hídrica que se instalou na cidade de São Paulo, um estudante, após a aula de hidrostática, resolveu colocar uma garrafa de 1,0 litro, cheia de água, no interior da caixa acoplada de descarga. Essa medida gerou uma economia de água no final de um período. Essa ideia colocada em prática foi baseada no
a) Princípio de Stevin.
b) Princípio de Arquimedes.
c) Princípio de Pascal.
d) Princípio dos vasos comunicantes.
e) Teorema de Bernoulli.
Resolução comentada
HIDROSTÁTICA – 2017 – 2016 e 2015
Densidade e Pressão
01- Para essa questão apenas utilizaremos a fórmula da pressão:
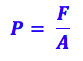
Onde:
P é a pressão
F é a força exercida
A é a área aonde essa força foi exercida
Bom, como foi dito no próprio exercício essa pressão se deve ao peso da coluna de ar, então podemos substituir essa força por m.g:
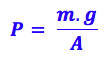 Isolando
a massa:
Isolando
a massa:
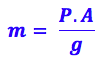 Colocando
os valores:
Colocando
os valores:
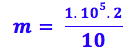 m
= 2.104 Kg
m
= 2.104 Kg
R – C
02-
01) Pressão é uma grandeza vetorial, portanto tem módulo, direção e sentido definidos
01.
Falsa ![]() Se
a força
Se
a força ![]() estiver
inclinada de um ângulo
β em
relação à horizontal, a parcela dessa
estiver
inclinada de um ângulo
β em
relação à horizontal, a parcela dessa
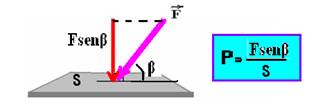
força que
exerce a pressão é a componente
vertical de ![]() ,
ou seja, é Fsenβ, conforme a figura acima.
,
ou seja, é Fsenβ, conforme a figura acima.
A
pressão sempre vai estar relacionada ao módulo
da força que age perpendicularmente à
superfície.
Então, não
importa a direção que
a força é aplicada, ela não
muda a direção da pressão,
que é sempre perpendicular
a superfície.
Só o
que leva em conta na pressão, portanto, é a intensidade.
02) A diferença de pressão entre dois pontos no interior de um líquido homogêneo e em equilíbrio é
proporcional à diferença de profundidade entre esses dois pontos.
02.
Correta ![]() Teorema
de Stevin
Teorema
de Stevin ![]() Observe
a figura abaixo onde, quem varia é apenas
a pressão vertical,
onde o líquido que é homogêneo e incompressível está em
equilíbrio.
Observe
a figura abaixo onde, quem varia é apenas
a pressão vertical,
onde o líquido que é homogêneo e incompressível está em
equilíbrio.
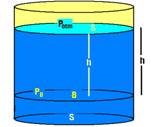
Na superfície livre superior (A) desse líquido age a pressão atmosférica (Patm), exercida pela coluna de ar que está sobre ele. Num ponto qualquer B do interior do líquido, a pressão (PB) que age é a soma da pressão atmosférica com a pressão exercida pela coluna líquida acima dele, devido à seu peso.
PB=Patm + Plíquido — PB=Patm + F/S — PB= Patm + peso do líquido/S — PB=Patm + (mlíquido.g)/S — dlíquido=mlíquido/Vlíquido — dlíquido=mlíquido/S.h — mlíquido=dlíquido.S.h — PB=Patm + (dlíquido.S.h)/S — PB=Patm+ dlíquido.g.h — esta expressão é chamada de Teorema Fundamental da Hidrostática ou de Teorema de Stevin

04) No sistema internacional de medidas (SI) a unidade de pressão é o Pascal (Pa).
04.
Correta ![]() Pa
= N/m2.
Pa
= N/m2.
08) Quando um dado ponto de um líquido em equilíbrio no interior de um recipiente sofre uma variação de pressão, essa variação de pressão é transmitida a todos os pontos do líquido e das paredes do recipiente.
08.
Correta ![]() Considere
um fluido (líquidos
e gases que fluem para as regiões inferiores de um recipiente até
preenchê-los totalmente) emequilíbrio
(vertical e horizontal) no
interior de um recipiente.
Considere
um fluido (líquidos
e gases que fluem para as regiões inferiores de um recipiente até
preenchê-los totalmente) emequilíbrio
(vertical e horizontal) no
interior de um recipiente.
Esse líquido exerce sobre as paredes do recipiente que o contem forças que se tornam de maior intensidade à medida que a profundidade aumenta.
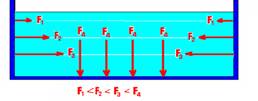
Observe que as forças, na mesma horizontal, em ambos os extremos, tem a mesma intensidade, pois o líquido está em equilíbrio horizontal, caso contrário, ele se moveria nessa direção.
16) Estando um líquido em um recipiente aberto, a pressão na superfície do líquido é nula.
16.
Falsa ![]() veja
02.
veja
02.
R- (02 + 04 + 08) = 14
03-
F
= ? ![]() S
= 1,0
mm2 =
1,0.10-6 m2
S
= 1,0
mm2 =
1,0.10-6 m2 ![]() a pressão
sistólica (sangue)
de valor Ps =
1,0.105.160
= 160.105 Pa
(N/m2)
que é a pressão exercida por uma coluna de h = 160 mm = 0,16 m de
mercúrio, de
valor
a pressão
sistólica (sangue)
de valor Ps =
1,0.105.160
= 160.105 Pa
(N/m2)
que é a pressão exercida por uma coluna de h = 160 mm = 0,16 m de
mercúrio, de
valor ![]() PHg =
d.g.h =
13,6.103.10.16.10-2 =
217,6.102
PHg =
d.g.h =
13,6.103.10.16.10-2 =
217,6.102
![]() PHg =
21760 Pa (N/m2).
PHg =
21760 Pa (N/m2).
É essa pressão (21760 Pa) devido à coluna de Hg (mecânica) que age sobre a área S = 1,0.
10-6 m2, devido
à força de
intensidade F
tal que P = ![]()
![]() 21760
=
21760
= ![]()
![]() F
= 2,176.
F
= 2,176.
10-2 N.
Teorema de Stevin – pressão hidrostática - vasos comunicantes
04- Devido ao teorema de Stevin, P=dlíquido.g.h, para um mesmo líquido, quanto maior a profundidade, maior será a pressão. Observe na figura abaixo, onde a esfera está imersa, que
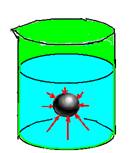
as forças exercidas pelo líquido sobre ela são maiores nas áreas inferiores (onde h é maior) que nas superiores (onde hé menor). A força resultante de todas essas forças está dirigida para cima, e corresponde ao empuxo que age sobre essa esfera. Nas laterais essas forças se anulam,
R- E
05-
a) Se
o processo ocorre à temperatura
constante trata-se
de uma transformação isotérmica e,
aplicando a equação dos gases ideais ![]() Po.Vo/To =
P.V/T
Po.Vo/To =
P.V/T ![]() Po.Vo =
P.V
Po.Vo =
P.V ![]() volume
inicial de ar no tubo cilíndrico de área da base S
volume
inicial de ar no tubo cilíndrico de área da base S ![]() Vo
Vo ![]() volume
final de ar no tubo cilíndrico
volume
final de ar no tubo cilíndrico ![]() V
=(4/5)Vo
V
=(4/5)Vo ![]() Po =
1 atm
Po =
1 atm ![]() Po.Vo =
P.V
Po.Vo =
P.V ![]() 1.Vo =
P.(4/5)Vo
1.Vo =
P.(4/5)Vo ![]() P
= 5/4
P
= 5/4 ![]() P
= 1,25 atm.
P
= 1,25 atm.


Mas,
uma das consequências do princípio de Stevin é que todos
os pontos do mesmo nível horizontal
suportam a mesma pressão ![]() PM =
PN
PM =
PN
![]() 1,35.105 =
105 +
104
H
1,35.105 =
105 +
104
H ![]() 1,35.105 –
1,0.105 =
104
H
1,35.105 –
1,0.105 =
104
H ![]() H
= 0,35.105
/104
H
= 0,35.105
/104
![]() H
= 0,35.10
H
= 0,35.10 ![]() H
= 3,5m
H
= 3,5m
06-
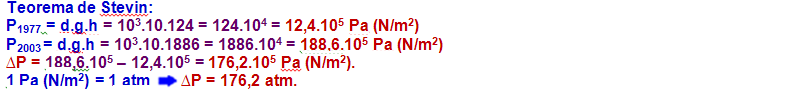
07- A pressão total no fundo do lago devido apenas à agua vale P = 5 atm – 1 atm = 4 atm.
Como para cada 1 atm de pressão a altura equivale a 10m, o lago terá h = 4×10 = 40 m de profundidade.
R- A
Experiência de Torricelli
08-
a) Se
o processo ocorre à temperatura
constante trata-se
de uma transformação isotérmica e,
aplicando a equação dos gases ideais ![]() Po.Vo/To =
P.V/T
Po.Vo/To =
P.V/T ![]() Po.Vo =
P.V
Po.Vo =
P.V ![]() volume
inicial de ar no tubo cilíndrico de área da base S
volume
inicial de ar no tubo cilíndrico de área da base S ![]() Vo
Vo ![]() volume
final de ar no tubo cilíndrico
volume
final de ar no tubo cilíndrico ![]() V
=(4/5)Vo
V
=(4/5)Vo ![]() Po =
1 atm
Po =
1 atm ![]() Po.Vo =
P.V
Po.Vo =
P.V ![]() 1.Vo =
P.(4/5)Vo
1.Vo =
P.(4/5)Vo ![]() P
= 5/4
P
= 5/4 ![]() P
= 1,25 atm.
P
= 1,25 atm.


Mas,
uma das consequências do princípio de Stevin é que todos
os pontos do mesmo nível horizontal
suportam a mesma pressão ![]() PM =
PN
PM =
PN
![]() 1,35.105 =
105 +
104
H
1,35.105 =
105 +
104
H ![]() 1,35.105 –
1,0.105 =
104
H
1,35.105 –
1,0.105 =
104
H ![]() H
= 0,35.105
/104
H
= 0,35.105
/104
![]() H
= 0,35.10
H
= 0,35.10 ![]() H
= 3,5m
H
= 3,5m
Princípio de Pascal
09-

Teorema de Arquimedes – Empuxo
10- Enunciado do princípio de Arquimedes:
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
R- A
11-

12-
Enunciado do princípio de Arquimedes
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força dedireção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
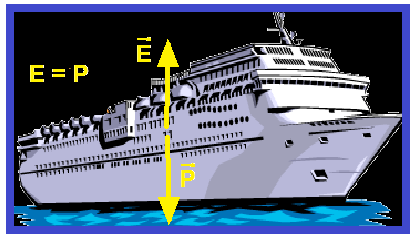
Como o navio está em equilíbrio vertical (flutuando) o empuxo (peso do volume do líquido deslocado), vertical e para cima deve ser igual ao peso do navio, vertical e para baixo.
R- C
13-

R- C
14-

15- Para esse exercício precisamos analisar a fórmula do empuxo:
E = dF.VFd.g

Onde:
E é o empuxo
![]() é
a densidade do fluído
é
a densidade do fluído
VFd é o volume de fluído deslocado
g é a aceleração da gravidade
Com a adição de sal a densidade da água aumenta, porém quando se aumenta a densidade parte da esfera sai da água, e o volume deslocado diminui, sendo assim a alternativa D é a correta, pois o empuxo não se altera, já que o peso da esfera é o mesmo em ambos os casos.
16-
![]()

Massa
do corpo sólido ![]() ms =
600g
ms =
600g ![]() Vsólido =
1 L =
103 cm3
Vsólido =
1 L =
103 cm3 ![]() densidade
do corpo sólido
densidade
do corpo sólido ![]() ds =
ds = ![]()
![]() ds =
ds = ![]()
![]() ds =
0,6 g/cm3.
ds =
0,6 g/cm3.
Volume total = 1,0.10 3 cm3
Volume imerso = 80% do Vtotal = 0,8.103 cm3.
![]() =
= ![]()
![]()
![]() =
= ![]()
![]() dl´quido =
dl´quido = ![]() =
0,75 g/cm3.
=
0,75 g/cm3.
R- B
17- Para que a pessoa + peso fique em equilíbrio é necessário que o empuxo (força vertical e para cima) equilibre os pesos da pessoa (Pp) somado ao peso do objetos (Po), verticais e para baixo.
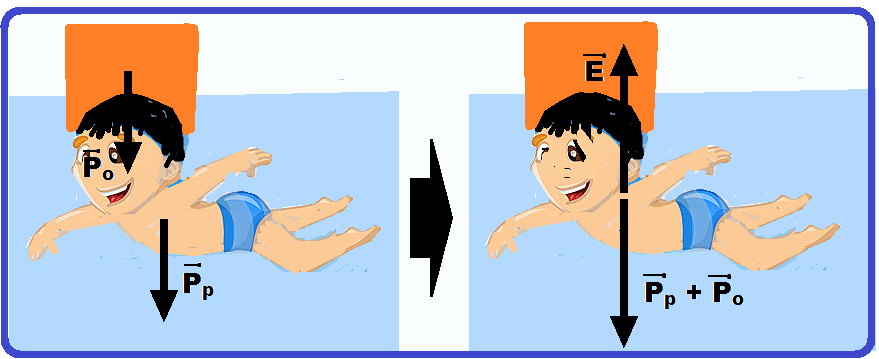
E
= Pp + Po =
mp.g + Po = 70.10 + Po ![]() E
= 700 + Po.
E
= 700 + Po.
Pessoa ![]() dpessoa =
dpessoa = ![]()
![]() 0,93.103 =
0,93.103 = ![]()
![]() Vpessoa =
Vpessoa = ![]()
![]() Vpessoa =
Vpessoa = ![]() =
75,27.10-3 m3.
=
75,27.10-3 m3.
Empuxo
sobre a pessoa totalmente imersa ![]() E
= dágua.Vpessoa.g =
103
E
= dágua.Vpessoa.g =
103![]() .
75,27.10-3.10
.
75,27.10-3.10 ![]() E
= 752,7 N.
E
= 752,7 N.
E
= 700 + Po ![]() 752,7 =
700 + Po
752,7 =
700 + Po ![]() Po =
752,7 – 700
Po =
752,7 – 700 ![]() Po =
52,7 N.
Po =
52,7 N.
18-
Teorema de Arquimedes – Empuxo
“Todo corpototal ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força dedireção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“

No caso do exercício peso total = peso da embarcação = mg=10.000×10 = 100.000 N + peso dos dois caminhões = 2.mg = 2.10.000×10 = 200.000 N + peso da carga dos dois caminhões = 2.m.10 =20m.
Ptotal =300.000 + 20m sendo m a massa de cada caminhão.
Volume
imerso = Vi = área
da base x altura = 10.10.0,4 ![]() Vi =40m2.
Vi =40m2.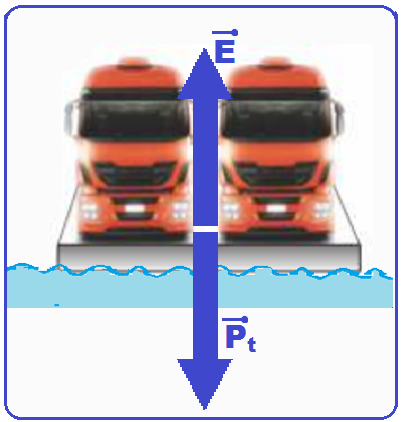
Densidade
da água ![]() da =
1g/c3 = 103
kg/m3.
da =
1g/c3 = 103
kg/m3.
Cálculo
do empuxo ![]() E
= da.Vi.g =
103.40.10
E
= da.Vi.g =
103.40.10![]() E
= 400.000 N
E
= 400.000 N
Como
flutua parcialmente imerso está em equilíbrio vertical e a força
resultante sobre ele é nula, assim o peso total deve anular o
empuxo![]() Pt =
E
Pt =
E ![]() 300.000
+ 20m = 400.000
300.000
+ 20m = 400.000 ![]() m
= 100.000/20
m
= 100.000/20![]() m
= 5.000 kg.
m
= 5.000 kg.
R- D
19- De acordo com o Princípio de Arquimedes todo corpo imerso sofre ação de uma força, denominada empuxo, que é vertical para cima, sua intensidade é igual ao peso do fluido deslocado pelo corpo. No caso do estudante, o volume deslocado foi utilizado, visto que a garrafa sempre estaria ocupando esse volume, com isso ele economizou, pois o vaso não enche tanto, não gasta tanta água e ainda por cima não interfere no rendimento da descarga.
R- A
HIDROSTÁTICA – 2013 - 2014
01-(FUVEST-SP-014)

Um bloco de madeira impermeável, de massa M e dimensões 2x3x3cm3, é inserido muito lentamente na água de um balde, até a condição de equilíbrio, com metade de seu volume submersa. A água que vaza do balde é coletada e num copo e tem massa m. A figura ilustra as situações inicial e final; em ambos os casos, o balde encontra-se cheio de água até sua capacidade máxima.

A relação entre as massas m e M é tal que
![]()
02-(MACKENZIE-SP-014)

Certa piscina contém água, de índice de refração absoluto igual a 4/3, e sua base se encontra 3,00 m

abaixo da superfície livre. Quando uma pessoa, na beira da piscina, olha perpendicularmente para seu fundo (base), terá a impressão de vê-lo Dado: Índice de refração absoluto do ar n = 1
a) 2,25 m mais próximo, em relação à profundidade real.
b) 1,33 m mais próximo, em relação à profundidade real.
c) 0,75 m mais próximo, em relação à profundidade real.
d) 1,33 m mais distante, em relação à profundidade real.
e) 0,75 m mais distante, em relação à profundidade real.
03-(UNESP-SP-014)

Um reservatório tem a forma de um paralelepípedo reto-retângulo com dimensões 2 m, 3 m e 4 m. A figura 1 o representa apoiado sobre uma superfície plana horizontal, com determinado volume de água dentro dele, até a altura de 2 m. Nessa situação, a pressão hidrostática exercida pela água no fundo do reservatório é P1.

A figura 2 representa o mesmo reservatório apoiado de um modo diferente sobre a mesma superfície horizontal e com a mesma quantidade de água dentro dele.

Considerando o sistema em equilíbrio nas duas situações e sendo P2 a pressão hidrostática exercida pela água no fundo do reservatório na segunda situação, é correto afirmar que

04-(UNICAMP-SP-014)

Uma boia de sinalização marítima muito simples pode ser construída unindo-se dois cilindros de mesmas dimensões e de densidades diferentes, sendo um de densidade menor e outro de densidade maior que a da água, tal como esquematizado na figura abaixo. Submergindo-se totalmente esta boia de sinalização na água, quais serão os pontos efetivos mais prováveis de aplicação das forças Peso e Empuxo?

a) Peso em B e Empuxo em B.
b) Peso em C e Empuxo em A.
c) Peso em C e Empuxo em B.
d) Peso em B e Empuxo em C
05-(PUC-MG-014)

Uma bola plástica cheia de ar está presa no fundo de uma piscina. Essa bola se solta e sobe até à

superfície. A bola se desloca em direção à superfície, porque:
a) a água da piscina faz uma força sobre a bola denominada empuxo.
b) o empuxo da água é maior que o peso da bola, enquanto a mesma estiver submersa.
c) enquanto a bola estiver flutuando na superfície da água, seu peso é maior que o empuxo.
d) a densidade da bola e a da água são iguais
06-(PUC-PR-014)


07-(PUC-RJ-014)

Um objeto feito de um material cuja massa específica é de 600 kg/m3 flutua com 3/4 de seu volume

submerso em um líquido cuja a massa específica é desconhecida. Calcule a massa específica deste líquido em g/cm3.
![]()
08-(UCPel-RS-014)

Um objeto maciço flutua com 1/3 de seu volume acima da superfície de certo líquido. Assinale a

alternativa que contém a expressão que relaciona a massa específica ρo desse objeto em função da
massa específica ρ do líquido, e que, também, apresenta a consideração inicial que permite
chegarmos à expressão correta.
(A) ρo = 3ρ/2 , a força de empuxo equivale a 1/3 da força peso.
(B) ρo = ρ/3 , a força de empuxo deve ser igual a 2/3 da força peso.
(C) ρo = (2/3)ρ , a força de empuxo deve ser igual a massa do objeto multiplicada pela aceleração
da gravidade local.
(D) ρo = ρ , a força de empuxo é igual à força peso.
(E) Não é possível encontrar a expressão, pois não é conhecido o volume do objeto, nem sua
massa.
09-(UDESC-SC-014)

Considere as proposições relacionadas aos fluidos hidrostáticos.
I. A pressão diminui com a altitude acima do nível do mar e aumenta com a profundidade abaixo da interface ar-água.
II. O elevador hidráulico é baseado no Princípio de Pascal.
III. Sabendo-se que a densidade do gelo, do óleo e da água são iguais a 0,92 g/cm3; 0,80 g/cm3 e 1,0 g/
cm3, respectivamente, pode-se afirmar que o gelo afunda no óleo e flutua na água.
IV. O peso aparente de um corpo completamente imerso é menor que o peso real, devido à ação da força de empuxo, exercida pelo líquido sobre o corpo, de cima para baixo.
Assinale a alternativa correta.
A. ( ) Somente as afirmativas I, II e III são verdadeiras.
B. ( ) Somente as afirmativas II e IV são verdadeiras.
C. ( ) Somente as afirmativas I e II são verdadeiras.
D. ( ) Somente as afirmativas I, III e IV são verdadeiras.
E. ( ) Todas as afirmativas são verdadeiras.
10-(UECE-CE-014)

Três sólidos, um cubo, um cilindro e uma esfera, têm massas iguais e distribuídas
homogeneamente ao longo de seus volumes. Os sólidos flutuam parcialmente submersos em um

mesmo líquido. A relação entre os volumes submersos de cada objeto é
A) Δcub > Δcil > Δesf .
B) Δcub = Δcil > Δesf .
C) Δcub > Δcil = Δesf .
D) Δcub = Δcil = Δesf .
11-(UECE-CE-014)

Considere um cubo imerso em água, conforme a figura a seguir.

No ponto destacado de uma das faces desse cubo, há uma força devido à pressão hidrostática exercida pela água. Assinale o vetor que melhor representa essa força.
![]()
12-(UFJF-MG-014)

A figura mostra um tubo em forma de U, aberto nas extremidades, contendo água e mercúrio em equilíbrio. Sendo h1 a

diferença de alturas dos níveis de água nos dois ramos, x a profundidade da coluna de água no ramo da direita, h2 diferença de alturas entre os níveis de mercúrio nos dois ramos do tubo e sabendo-se que a pressão atmosférica é patm, calcule:
a) A pressão na interface água-mercúrio no ramo esquerdo do tubo.
b) A altura h1 em função da altura h2, da densidade da água (ρa) e da densidade do mercúrio (ρm).
13-(UFPA-PA-014)

Uma criança brinca com um balde de água, um barquinho e uma âncora de metal. Na situação “A”,

a criança coloca o barquinho flutuando na água. Na situação “B”, coloca o barquinho flutuando com a âncora dentro do barquinho. Na situação “C”, joga a âncora no fundo do balde e o barquinho flutuando na superfície da água. Denotemos por NA, NB e NC, as alturas da superfície da água do balde nas situações “A”, “B” e “C” respectivamente. Use a lei de Arquimedes para determinar qual das seguintes alternativas é a correta.
(A) NA > NB > NC
(B) NC > NB > NA
(C) NB > NC > NA
(D) NA > NC > NB
(E) NC > NB > NA
14-(UFPR-PR-014)

Com o objetivo de encontrar grande quantidade de seres vivos nas profundezas do mar, pesquisadores utilizando um submarino chegaram até a profundidade de 3.600 m no Platô de São

Paulo. A pressão interna no submarino foi mantida igual à pressão atmosférica ao nível do mar. Considere que a pressão atmosférica ao nível do mar é de 1,0.105 N/m2, a aceleração da gravidade é 10 m/s² e que a densidade da água seja constante e igual a 1,0.10³ kg/m³. Com base nos
conceitos de hidrostática, assinale a alternativa que indica quantas vezes a pressão externa da água sobre o submarino, naquela profundidade, é maior que a pressão no seu interior, se o submarino repousa no fundo do platô.
![]()
15-(UFSM-RS-014)

O mergulho profundo pode causar problemas de saúde ao mergulhador devido à alta pressão. Num

mar de águas calmas,
I - a pressão sobre o mergulhador aumenta aproximadamente 1 atm a cada 10m de profundidade.
II - o módulo da força de empuxo que atua sobre o mergulhador cresce linearmente com a profundidade.
III - a diferença de pressão entre os pés e a cabeça do mergulhador, num mergulho vertical, é
praticamente independente da profundidade.
Está(ão) correta(s)
![]()
16-(UNEAL-AL-014)

O procedimento adotado para medir a pressão de uma amostra de gás em um
laboratório, onde o módulo da aceleração da gravidade é 10m/s2, está esquematizado
nas figuras.

Na figura I, um reservatório, R, cheio de gás, encontra-se ligado a um manômetro de tubo aberto contendo mercúrio de densidade 13,6g/cm3 e, na figura II, um tubo capilar com a sua extremidade superior fechada está mergulhado em um recipiente aberto contendo mercúrio.
Nessas condições, a pressão exercida pelo gás, em 105 pascal, é de, aproximadamente,
![]()
Densidade e pressão
47-(UEM-PR-013)

Analise as alternativas abaixo e assinale o que for correto.

01) No Sistema Internacional de Unidades, a unidade de densidade volumétrica é o kg/m3.
02) A pressão é uma grandeza escalar.
04) A diferença de pressão entre dois pontos no interior de um líquido homogêneo em repouso é proporcional à diferença da altura entre esses dois pontos.
08) A pressão que uma força exerce sobre um objeto é diretamente proporcional à área sobre a qual a força é aplicada.
16) Quando um corpo é imerso em um líquido, uma força, na direção vertical, é exercida sobre o corpo, e o módulo dessa força é diretamente proporcional ao volume do líquido deslocado
48-(PUC-RJ-013)

Um recipiente contém 0,0100 m3 de água e 2000 cm3 de óleo. Considerando-se a densidade da água

1,00 g/cm3 e a densidade do óleo 0,900 g/cm3, a massa, medida em quilogramas, da mistura destes líquidos é:
(A) 11,8 (B) 101,8 (C) 2,8 (D) 28 (E) 118
Teorema de Stevin – pressão hidrostática - vasos comunicantes
37-(UNESP-SP-013)

O relevo submarino de determinada região está representado pelas curvas de nível mostradas na figura, na qual os valores em metros representam as alturas verticais medidas em relação ao nível de referência mais profundo, mostrado pela linha vermelha.

Dois peixes, 1 e 2, estão inicialmente em repouso nas posições indicadas e deslocam-se para o ponto P, onde param novamente. Considere que toda a região mostrada na figura esteja submersa, que a água do mar esteja em equilíbrio e que sua densidade seja igual a 103 kg/m3. Se g = 10 m/s2 e 1 atm = 105 Pa, pode-se afirmar, considerando-se apenas os pontos de partida e de chegada, que, durante seu movimento, o peixe
(A) 2 sofreu uma redução de pressão de 3 atm. (B) 1 sofreu um aumento de pressão de 4 atm.
(C) 1 sofreu um aumento de pressão de 6 atm. (D) 2 sofreu uma redução de pressão de 6 atm.
(E) 1 sofreu uma redução de pressão de 3 atm.
38-(ENEM-MEC-012)

O manual que acompanha uma ducha higiênica informa que a pressão mínima da água para o seu funcionamento apropriado é de 20 kPa. A figura mostra a instalação hidráulica com a caixa d’água e o cano ao qual deve ser conectada a ducha.

O valor da pressão da água na ducha está associado à altura
a) h1 b h2 c) h3 d h4 e h5
Experiência de Torricelli
35-(UNESP-SP-013)

Seis reservatórios cilíndricos, superiormente abertos e idênticos (A, B, C, D, E e F) estão apoiados sobre uma superfície horizontal plana e ligados por válvulas (V) nas posições indicadas na figura.

Com as válvulas (V) fechadas, cada reservatório contém água até o nível (h) indicado na figura. Todas as válvulas são, então, abertas, o que permite a passagem livre da água entre os reservatórios, até que se estabeleça o equilíbrio hidrostático. Nesta situação final, o nível da água, em dm, será igual a
(A) 6,0 nos reservatórios de A a E e 3,0 no reservatório F.
(B) 5,5 nos reservatórios de A a E e 3,0 no reservatório F.
(C) 6,0 em todos os reservatórios.
(D) 5,5 em todos os reservatórios.
(E) 5,0 nos reservatórios de A a E e 3,0 no reservatório F.
Princípio de Pascal
25-UERJ-RJ-013)

Observe, na figura a seguir, a representação de uma prensa hidráulica, na qual as forças F1 e F2 atuam, respectivamente, sobre os êmbolos dos cilindros I e II.

Admita que os cilindros estejam totalmente preenchidos por um líquido.
O volume do cilindro II é igual a quatro vezes o volume do cilindro I, cuja altura é o triplo da altura do cilindro II.
A razão F2/F1 entre as intensidades das forças, quando o sistema está em equilíbrio, corresponde a:
(A) 12 (B) 6 (C) 3 (D) 2
26-(ESPCEX-013)

Um elevador hidráulico de um posto de gasolina é acionado por um pequeno êmbolo de área igual a 4.10-4 m2.
O automóvel a ser elevado tem peso de 2.104N e está sobre o êmbolo maior de área 0,16m2.
A intensidade mínima da força que dever ser aplicada ao êmbolo menor para conseguir elevar o automóvel é de
a) 20 N b) 40 N c) 50 N d) 80 N e) 120 N
27-(UNESP-SP-013)

O sifão é um dispositivo que permite transferir um líquido de um recipiente mais alto para outro mais baixo, por meio, por exemplo, de uma mangueira cheia do mesmo líquido. Na figura, que representa, esquematicamente, um sifão utilizado para transferir água de um recipiente sobre uma mesa para outro no piso, R é um registro que, quando fechado, impede o movimento da água. Quando o registro é aberto, a diferença de pressão entre os pontos A e B provoca o escoamento da água para o recipiente de baixo.

Considere que os dois recipientes estejam abertos para a atmosfera, que a densidade da água seja igual a 103 kg/m3
e que g = 10 m/s2. De acordo com as medidas indicadas na figura, com o registro R fechado, a diferença de pressão
PA - PB, entre os pontos A e B, em pascal, é igual a
(A) 4000. (B) 10000. (C) 2000. (D) 8000. (E) 12000
Teorema de Arquimedes – Empuxo
67-(UNIFESP-SP-013)

Um objeto maciço cilíndrico, de diâmetro igual a 2,0 cm, é composto de duas partes cilíndricas distintas, unidas por uma cola de massa desprezível. A primeira parte, com 5,0 cm de altura, é composta por uma cortiça com densidade volumétrica 0,20 g/cm3.
A segunda parte, de 0,5 cm de altura, é composta por uma liga metálica de densidade volumétrica 8,0 g/cm3. Conforme indica a figura, o objeto encontra-se em repouso, parcialmente submerso na água, cuja densidade volumétrica é 1,0 g/cm3.

Nas condições descritas relativas ao equilíbrio mecânico do objeto e considerando π aproximadamente igual a 3, determine:
a) a massa total, em gramas, do objeto cilíndrico.
b) a altura, em centímetros, da parte do cilindro submerso na água.
68-(UFV-MG-013)

Para poder emergir e submergir (afundar), um submarino utiliza tanques de lastro. Esses tanques ficam vazios quando o submarino está na superfície da água e se enchem de água do mar, de modo a permitir sua submersão.

As figuras A, B e C ilustram, respectivamente, situações em que um submarino encontra-se na superfície, submergindo e totalmente submerso. Sabendo que a água do mar tem densidade de aproximadamente 1000 kg/m3, que o volume de um submarino é de 1500 m3 e quesua massa (sem lastro) é de 1300 ton (toneladas), o volume de água necessário para que o submarino permaneça totalmente submerso e em equilíbrio é igual a:
a) 300 m3 b) 200 m3 c) 500 m3 d) 100 m3
69-(UFV-MG-013)

As medidas aproximadas do transatlântico Costa Concórdia, que colidiu recentemente com uma pedra são:

massa de 1,2.108kg, comprimento de 300 m, largura de 40 m e altura de 60 m. Supondo que o formato do navio seja o de um paralelepípedo, podemos estimar a profundidade mínima que o mar deve possuir para que o navio possa flutuar livremente. Considerando que o módulo da aceleração gravitacional é 10 m/s2 e a densidade da água do mar como sendo de 1 g/cm3, é CORRETO afirmar que essa profundidade mínima é:
a) 10,0 m b) 50,0 m c) 06,7 m d) 53,3 m
70-(UFRN-RN-013)

Um balão de ar quente é constituído por um saco de tecido sintético, chamado envelope, o qual é capaz de conter ar aquecido.
Embaixo do envelope, há um cesto de vime, para o transporte de passageiros, e uma fonte de calor, conforme ilustra a figura a seguir.

Para que o balão suba, aquece-se o ar no interior do envelope e, com isso, inicia-se a flutuação do balão. Essa flutuação ocorre porque, com o aquecimento do ar no interior do envelope,
A) a densidade do ar diminui, tornando o peso do balão menor que o empuxo.
B) a pressão externa do ar sobre o balão aumenta, tornando seu peso menor que o empuxo.
C) a densidade do ar diminui, tornando o peso do balão maior que o empuxo.
D) a pressão externa do ar sobre o balão aumenta, tornando seu peso maior que o empuxo.
Resolução comentada
HIDROSTÁTICA – 2014 – 2013.
01- O Empuxo (força vertical e para cima) corresponde ao peso do volume de líquido (no caso,

água)deslocado pela parte imersa do bloco e, pelo enunciado esse volume tem massa m com peso fornecido por Págua=m.g=E--- por outro lado, o bloco encontra-se em equilíbrio (força resultante nula) flutuando na água
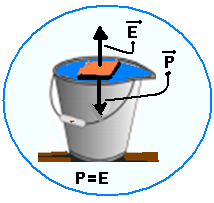
e assim, seu peso Pbloco (vertical e para baixo) deve anular o empuxo E (vertical e para cima) --- Pbloco=M.g=E=Págua--- m,g = M.g --- m=M --- R- C
02- A imagem vista pelo observador é virtual e está sempre acima do objeto e, ambos na mesma
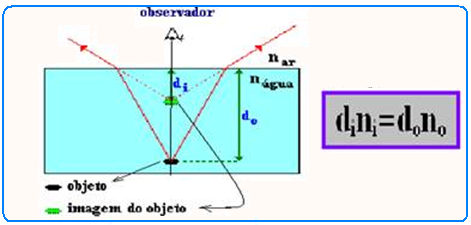
reta vertical, onde:
di---- distância vertical da imagem à superfície de separação (interface) água-ar (distância aparente, em que o observador enxerga a imagem)
do---- distância vertical do objeto, até a superfície de separação (interface) água-ar.
no---- índice de refração do meio onde está o observador (no caso, ar)
ni---- índice de refração do meio onde está o objeto a imagem (no caso, água)
Pelas informações do exercício:

Então, o observador verá a imagem do fundo da piscina a uma distância di=2,25m abaixo da superfície da

água e, terá a impressão de vê-lo a uma altura h=3,00 – 2,25 = 0,75 m mais próximo em relação à profundidade real --- R- C
03-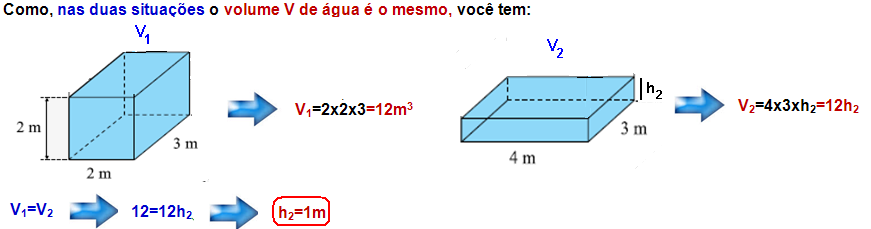
A pressão hidrostática no fundo de cada recipiente é fornecida pelo teorema de Stevin --- P= d.g. h . No volume 1 de altura 2m--- P1=dágua.g.h1= dágua.g.2 --- P1=2dágua.g.
No volume 2 de altura 1m --- P2=dágua.g.h2= dágua.g.1 --- P1=dágua.g.
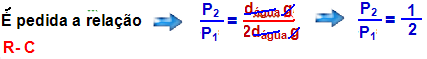
04- Peso --- sendo a densidade do cilindro do lado direito maior que a do cilindro do lado esquerdo, o cilindro do lado direito terá maior massa, pois d=m/v (nessa expressão, como o volume V é o mesmo a massa m é diretamente proporcional à densidade d) --- pela expressão P=m.g, quanto maior a massa maior o peso e o peso do cilindro direito é maior que o do cilindro esquerdo (ambos aplicados no centro geométrico) veja
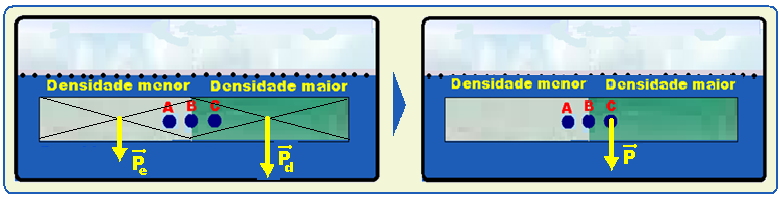
primeira figura --- assim, o peso da boia será deslocado para o lado direito (ponto B) figura da direita.
Empuxo --- Enunciado do princípio de Arquimedes:
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“
![]() Considere
um líquido de densidade dl contido
num recipiente R’ no nível indicado na figura I, onde está um
corpo sólido de densidade dctal
que dc >
dl.
Considere
um líquido de densidade dl contido
num recipiente R’ no nível indicado na figura I, onde está um
corpo sólido de densidade dctal
que dc >
dl.

Em seguida o corpo é colocado em R’ e fica totalmente imerso (dc > dl), expulsando um volume de líquido que é igual ao próprio volume do corpo. O volume total (V) do líquido deslocado é recolhido no recipiente R (figura II).
Se você pesar o volume V do líquido deslocado você obterá o valor do empuxo, que é uma força vertical e para cima --- empuxo=peso do volume de líquido deslocado (que é o mesmo volume que o do corpo, se totalmente imerso) --- E= Pl=mlg --- dl=ml/V --- ml=dl.Vl --- E=dl.Vl.g

No caso do exercício, com a boia totalmente imersa ela deslocará um volume de água igual ao seu próprio volume --- o empuxo, vertical e para cima, corresponde ao peso do volume de água deslocada e, como a água é um líquido homogêneo (mesma densidade em todos seus pontos) o empuxo será aplicado em seu
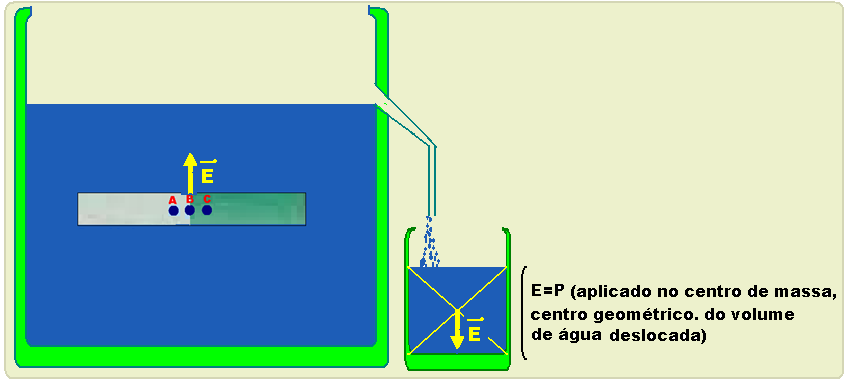
centro de massa que é onde é aplicado seu peso e que corresponde ao centro geométrico da boia
(ponto B) --- R- C
05- Sobre a bexiga imersa agem as forças (peso, vertical e para baixo) e o (empuxo, vertical e para cima), tal que:

R- B
06- Como, em ambos os casos a esfera está flutuando o empuxo em cada um deles é igual ao peso da esfera que é o mesmo, pois P=mg e a massa é a mesma para cada esfera --- já o líquido 2 é mais denso que o líquido 1, sendo mais pesado ficando mais embaixo, fazendo com que a esfera fique mais acima.
R- D
07- Como o objeto de volume V flutua no líquido ele está em equilíbrio e, nesse caso, o empuxo E
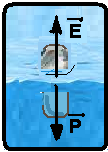
(força vertical e para cima) deve anular o peso P )força vertical e para baixo_.
Empuxo --- E = dlíquido.Vimerso.g= dlíquido.(3/4)V.g.
Peso do objeto de volume V --- P=dobjeto.V.g=600.10-3.V.g --- P=0,6Vg.
E = P --- dlíquido.(3/4)V.g = 0,6Vg --- dlíquido=2,4/3=0,8g/cm3
R- D
08- O objeto flutua (equilíbrio) com 2/3 de seu volume imerso Vi=V/3 --- E = P --- ρ.g.Vi =P --- ρ.g.2V/3 = ρo.g.V --- ρ.2/3 = ρo.
R- C
09- I. Correta --- a atmosfera terrestre é uma imensa camada de ar e outros gases, com dezenas de quilômetros de altura, que são atraídos pela gravidade da Terra e por isso, sua densidade é maior em pontos mais próximos da superfície. Ela atua como uma zona intermediária entre o espaço sideral e a Terra e acompanha todos os movimentos da Terra.



Essa camada gasosa exerce uma pressão sobre os corpos nela mergulhados, devida ao peso da coluna de ar que se encontra sobre esses corpos, e que é chamada de pressão atmosférica, sendo tanto maior quanto mais o corpo estiver mais perto da superfície da Terra.
II. Correta --- princípio enunciado por Pascal, físico e matemático francês (1623 – 1663), conhecido como princípio de Pascal:
“ O acréscimo de pressão exercido num ponto de um líquido ideal em equilíbrio é transmitida integralmente a todos os pontos desse líquido e também às paredes do recipiente onde está contido”
A maioria dos sistemas multiplicadores de forças é baseado no princípio de Pascal e, para explicá-lo considere um líquido ideal no interior de dois cilindros verticais de seções diferentes e interligados. Esses cilindros, em contato com a parte superior do líquido, possuem dois êmbolos de áreas S1 e S2.
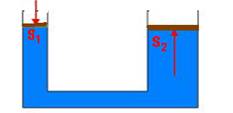
Uma força de intensidade F1 aplicada ao êmbolo de menor área (S1), provocará um aumento de pressão dado por ΔP=F1/S1 e, pelo princípio de Pascal esse acréscimo de pressão se transmitirá integralmente a todos os pontos do líquido e das paredes, inclusive para o êmbolo de maior área (S2). Então, o êmbolo maior fica sujeito a uma força F2, tal que ΔP=F2/S2. Pelo princípio de Pascal essa variação de pressão se transmite integralmente do êmbolo menor ao êmbolo maior e são iguais --- F1/S1=F2/S2

Observe na expressão acima que, como S2 > S1, tem-se que F2 > F1 e, assim, a intensidade da força é proporcional à área de cada êmbolo, ou seja, esse sistema é capaz de multiplicar forças.
![]() Exemplos
de sistemas multiplicadores de forças baseados no Princípio de
Pascal:
Exemplos
de sistemas multiplicadores de forças baseados no Princípio de
Pascal:
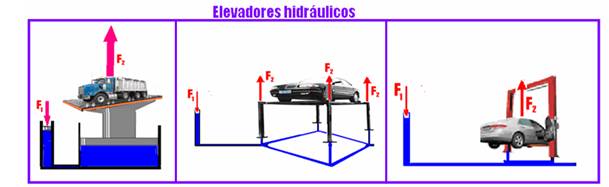
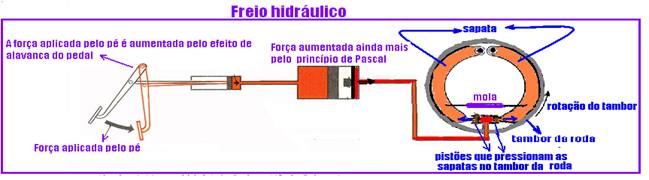

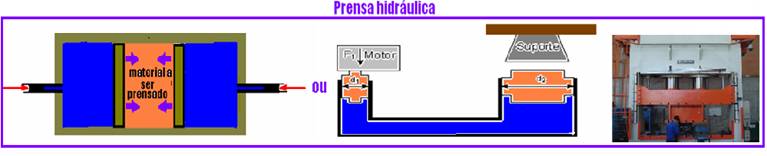
III. Correta --- os mais densos, mais pesados, ficam em baixo e os menos densos, mais leves, ficam em cima
IV. Falsa --- o empuxo é uma força exercida de baixo para cima sobre qualquer corpo imerso num fluido e é igual ao peso do volume de fluido deslocado “Principio de Arquimedes”
R- A
10- Peso de cada corpo --- Pc=dc.vcg=mcg --- Empuxo de cada corpo --- E=dL.Vi.g --- como estão flutuando estão em equilíbrio e P = E --- mc.g = dL.Vi.g --- Vi=mc/dL --- como a massa do corpo é a mesma e o líquido é o mesmo (mesma dL) o volume imerso é o mesmo para os três sólidos.
R- D
11- Pressão
(P) é
uma grandeza física obtida pelo quociente
entre a intensidade da força (![]() )
e a área (S) em
que a força se distribui. Observe
na figura
abaixo que a força (
)
e a área (S) em
que a força se distribui. Observe
na figura
abaixo que a força (![]() )
que produz a pressão sobre a área S é perpendicular à mesma.
)
que produz a pressão sobre a área S é perpendicular à mesma.

No caso do exercício a força é a hidrostática, devida à pressão hidrostática e também é
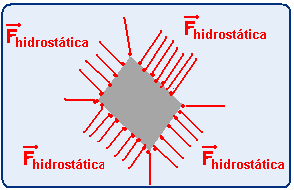
perpendicular à área da superfície em cada ponto.
R- A.
12- a) A pressão na interface água-mercúrio no ramo esquerdo do tubo (ponto k), pelo teorema de Stevin é dada por P

Stevin é dada por PK=Patm + ρágua.g.(h2 + x + h1), sendo ρágua a densidade da água.
b) Como conseqüência do teorema de Stevin, todos os pontos no mesmo nível horizontal suportam a
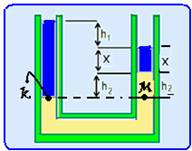
mesma pressão --- PK = PM --- Patm + ρágua.g.(h2 + x + h1 = ρmercúrio.g.h2 + ρágua.g.x + Patm --- ρágua.h2 + ρágua.h1 = ρmercúrio.h2 --- h1=(ρmercúrio - ρágua)/ ρágua.
13- O empuxo (força vertical e para cima) é igual ao peso do volume de líquido deslocado e assim, quanto maior o peso maior será o volume de líquido deslocado e consequentemente, maior será a altura da superfície da água do balde.
Maior peso B (barco + âncora dentro, deslocam maior volume de água) --- menor peso A (barco sem

âncora, desloca menor volume de água) --- intermediário C (volume deslocado somente pelo barco ) + volume deslocado somente pela âncora).
R- C
14- Pressão a que o submarino está sujeito no fundo do platô a uma profundidade de h=3600m --- teorema de Stevin --- Pf= Patm + dágua.g,h= 105 + 105.10.3600 --- Pf= 105 + 36.106 --- Pf=361.105 N/m2.
É pedida a relação Pf/Patm=361.105/105 = 361.
R- C
15- I. Correta.
II. Correta --- E=dágua.g.h --- observe nessa expressão que a relação entre E e h é uma função do primeiro grau.
III, Falsa --- Teorema de Stevin --- ΔP=d.g.h (a diferença de pressão é diretamente proporcional à altura h).
R. C
16- 05- A figura II indica o valor da pressão atmosférica Patm=dhg.g.h=13,6.103.10.0,75 --- Patm=1,02.105 Pa.
A pressão Pg exercida pelo gás é equilibrada pela pressão atmosférica (Patm=105Pa) somada à pressão devida ao mercúrio de densidade dhg=13,6g/cm3=13,6.103kg/m3 --- Pg= Patm + dhg.g.h= 1,02.105 + 13,6.103.10.0,25=1,02.105 + 34.103=1,02.105 + 0,34.105 --- Pg=1,36.105 Pa.
R- 01
Densidade e pressão
47- 01. Correta --- A densidade de um corpo (no caso um líquido) pode ser definida como sendo a grandeza física que fornece a quantidade de massa (matéria) de que está concentrada num determinado volume. Chamando de m a quantidade de massa contida em certo volume V, a expressão matemática da densidade é:
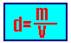
No Sistema Internacional de Unidades (SI) a unidade de densidade é o quilograma por metro cúbico (kg/m3), mas são usados também o grama por centímetro cúbico (g/cm3) e o quilograma por litro (kg/L). Relações:
1g=10--3kg --- 1cm3=10-6m3 --- 1g/cm3=103kg/m3 --- 1g/cm3=10-3kg/10-3L --- 1gcm3=1 kg/L
Regra prática:
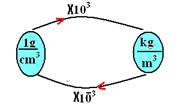
02. Correta --- a pressão sempre vai estar relacionada ao módulo da força que age perpendicularmente à superfície --- portanto, não importa em qual direção a força é exercida, ela na afeta a direção da pressão, que é sempre perpendicular a superfície --- assim, o que interessa é só a intensidade da pressão.
04. Correta --- A pressão exercida por uma coluna líquida não depende das dimensões do recipiente que a contém, mas apenas da natureza do líquido, fornecida pela sua densidade (d), do local (g) e da altura da coluna (h) --- entre dois pontos A e B de alturas hA e hB, a diferença de pressão é dada por (lei de Stevin) --- PA=dlíquido.g.hA --- PB=dlíquido.g.hB --- ∆P=PB – PA= dlíquido.g.hA - dlíquido.g.hB --- ∆P=dlíquido.g.(hA – hB).
08- Falsa --- são inversamente proporcionais --- P=F/A --- observe nessa fórmula que para uma mesma força, quanto menor a área maior será a pressão exercida pela força --- como exemplos práticos, observe as figuras abaixo:




16. Correta --- enunciado do princípio de Arquimedes:
“Todo corpo total ou parcialmente mergulhado num líquido em equilíbrio, recebe uma força de direção vertical e sentido para cima denominada de Empuxo, cuja intensidade é igual ao peso do volume de líquido deslocado“ --- trata-se do empuxo --- E=dlíquido.Vlíquido deslocado.g.
R- 01,02,04,16)
48- Água --- Va=0,01m3=0,01.103dm3 --- Va=10L --- da=1g/cm3=103kg/m3=103kg/103L --- da=1kg/L --- da=ma/Va --- 1=ma/10 --- ma=10L --- óleo --- Vo=2000cm3=2000.10-3dm3 --- Vo=2L --- do=0,9g/cm3=0,9.103kg/m3=0,9.103kg/103L --- do=0,9kg/L --- do=mo/Vo --- 0,9=mo/2 --- mo=1,8kg --- a massa da mistura vale m=10 + 1,8=11,8kg --- R- A.
Teorema de Stevin – Pressão hidrostática - Vasos comunicantes
37- Peixe 1 --- passou de 120m para 90m (desceu) --- ∆P=d.g.∆h=103.10.30=3.105Pa=3atm --- a
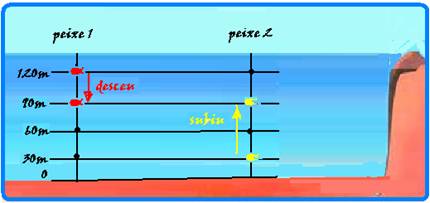
pressão aumentou --- peixe 2 --- passou de 30m para 90m (subiu) --- ∆P=d.g.∆h=103.10.60=6.105Pa=6atm --- a pressão diminuiu ---
R- D.
38- Teorema Fundamental da Hidrostática ou de Teorema de Stevin --- ∆P=dágua.g.h, onde P ´a pressão hidrostática no ponto de saída da água (onde está a ducha), g é a aceleração da gravidade local e h é altura medida desde qualquer
Ponto da superfície livre da água no interior da caixa d’água e o ponto de saída da mesma, onde está a ducha.
R- E.
Experiência de Torricelli
35- Os 5 primeiros cilindros estão ligados e, após abertas as válvulas eles atingirão o equilíbrio hidrostático e a altura final de cada um que deve ser a mesma (h) e dada por --- h=(8 + 7 + 6 + 5 + 4)/5=6dm --- observe na figura abaixo
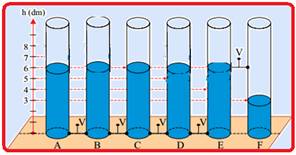
que a válvula que une E a F está na altura de 6dm e não escoará água de E para F que permanecerá na altura de 3dm ---
R- A.
Princípio de Pascal
25- Se você chamar V1=V --- V2=4V --- se você chamar h2=h --- h1=3h --- V2=S2.h2 --- V1=S1.h1 --- 4V = S2.h (I) --- V=S1.3h (II) --- (II) em (I) --- 4,3,S1.h = S2.h --- S2=12S1 --- estando o sistema em equilíbrio a pressão em cada recipiente é a mesma --- P1 = P2 --- F1/S1 = F2/S2 --- F1/S1 = F2/12S1 --- F1/F2=12 --- R- A.
26- A maioria dos sistemas multiplicadores de forças é baseado no princípio de Pascal e, para explicá-lo considere um líquido ideal no interior de dois cilindros verticais de seções diferentes e interligados. Esses cilindros, em contato com a parte superior do líquido, possuem dois êmbolos de áreas S1 e S2.

Uma força de intensidade F1 aplicada ao êmbolo de menor área (S1), provocará um aumento de pressão dado por ΔP=F1/S1 e, pelo princípio de Pascal esse acréscimo de pressão se transmitirá integralmente a todos os pontos do líquido e das paredes, inclusive para o êmbolo de maior área (S2). Então, o êmbolo maior fica sujeito a uma força F2, tal que ΔP=F2/S2. Pelo princípio de Pascal essa variação de pressão se transmite integralmente do êmbolo menor ao êmbolo maior e são iguais --- F1/S1=F2/S2

Observe na expressão acima que, como S2 > S1, tem-se que F2 > F1 e, assim, a intensidade da força é proporcional à área de cada êmbolo, ou seja, esse sistema é capaz de multiplicar forças.
Substituindo os valores fornecidos --- F1/4.10-4=2.104/0,16 --- F1=50N --- R- C.
27- Observe na figura que a pressão na superfície de cada recipiente é a mesma e é a pressão atmosférica --- no

recipiente da esquerda --- Patm=PA + dgh --- PA=Patm – dgh=Patm – 103.10.0,4 --- PA= Patm – 4.103 --- no recipiente da direita --- Patm=PB + dgh --- PB=Patm – dgh=Patm – 103.10.1,2 --- PB= Patm – 1,2.103 --- PA – PB= Patm – 4.103 – (Patm – 12.103)=Patm – 4.103 – Patm + 12.103 --- PA – PB=8.103=8000Pa --- R- D.
Teorema de Arquimedes – Empuxo
67- a) Área da base de cada cilindro A1=A2=A=π.R2=3.12 --- A=3cm2 --- volume do cilindro 1 --- V=A.h1=3.5 --- V1=15cm3 --- volume do cilindro 2 --- V=A.h2=3.0,5 --- V1=1,5cm3 --- massa do
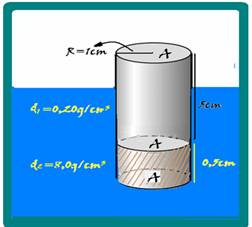
cilindro 1 --- d1=m1/V1 ---0,2=m1/15 --- m1=3g --- massa do cilindro 2 --- d2=m2/V2 --- 8=m2/1,5 --- m2=12g --- massa total --- m=3 + 12=15g --- m=15g ou m=15.10-3kg.
b) Peso do cilindro --- P=m.g=15.10-3.10 --- P=15.10-2N --- cálculo do empuxo sobre o cilindro com volume imerso Vi --- E=dágua.Vi.g=103.Vi.10 --- E=104Vi --- como o está em equilíbrio o peso deve anular o empuxo --- P=E ---
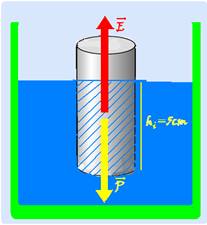
15.10-2 = 104Vi --- Vi=15.10-6m3 --- Vi=15cm3 --- altura (hi) da parte imersa --- Vi=S.hi --- 15=3.hi --- hi=5cm.
68- Peso do submarino sem lastro --- Ps=ms.g=13.105.10=13.106N --- empuxo com o submarino totalmente imerso --- E=dágua.Vs.g=103.15.102.10=15.106N --- peso do volume V’ de água (lastro) que o submarino deve receber para que fique totalmente imerso e em equilíbrio --- P’=dágua.V’.g=103.V’.10=104V’ --- como ele está em equilíbrio a intensidade da força resultante
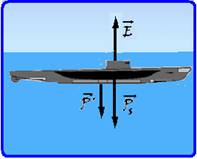
sobre ele deve ser nula --- E = Ps + P’ --- 15.106 = 13.106 + 104V’ --- V’=2.106/104=
2.102m3=200m3 --- R- B.
69- Peso do transatlântico --- P=mg=1,2.108.10=12.108N --- para que ele flutue sem tocar o fundo sua altura h deve ser tal que --- V=b,L,h=300.40.h=12,103h --- empuxo --- E=dágua.V.g. =
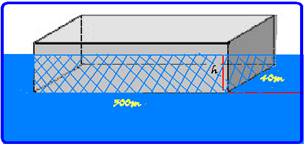
103.12.103h.10 = 12.107h --- como ele deve estar flutuando (em equilíbrio) --- E = P --- 12.107h=12.108 --- h=12.108/12.107 --- h=10m --- R- A.
70- Quando o ar do interior do balão é aquecido, ele se dilata, tornando sua densidade e, consequentemente seu peso menor --- quando o peso do balão (vertical e para baixo) fica menor que o empuxo sobre ele (vertical e para cima), o balão sobe --- R- A.
|
|
|
|